0402换元积分法-不定积分
文章目录
- 1 第一类换元法
- 1.1 定理1
- 1.2 例题
- 1.2 常见凑微分形式
- 1.2.1常见基本的导数公式的逆运算
- 1.2.2被积函数含有三角函数
- 2 第二类换元法
- 2.1 定理2
- 2.2 常见第二换元代换方法
- 2.2.1 三角代换-弦代换
- 2.2.2 三角代换-切代换
- 2.2.3 三角代换-割代换
- 2.2.4 三角代换汇总
- 2.2.5 倒代换
- 2.2.6 根式代换
- 3 积分推导公式
- 后记
把复合函数的微分法反过来用于求不定积分,利用中间变量的代换,得到复合函数的积分法,称为换元积分法。换元法分为两类。
1 第一类换元法
1.1 定理1
设f(u)f(u)f(u)具有原函数F(u)F(u)F(u),即
F′(u)=f(u),∫f(u)du=F(u)+CF^{'}(u)=f(u),\int{f(u)du}=F(u)+CF′(u)=f(u),∫f(u)du=F(u)+C
如果u是中间变量:u=ϕ(x),且设ϕ(x)u=\phi(x),且设\phi(x)u=ϕ(x),且设ϕ(x)可微,那么根据复合函数微分法,有
dF[ϕ(x)]=f[ϕ(x)]ϕ′(x)dxdF[\phi(x)]=f[\phi(x)]\phi^{'}(x)dxdF[ϕ(x)]=f[ϕ(x)]ϕ′(x)dx,
根据不定积分的定义就得
∫f[ϕ(x)]ϕ′(x)dx=F[ϕ(x)]+C=[∫f(u)du]u=ϕ(x)\int{f[\phi(x)]\phi^{'}(x)dx}=F[\phi(x)]+C=[\int{f(u)du}]_{u=\phi(x)}∫f[ϕ(x)]ϕ′(x)dx=F[ϕ(x)]+C=[∫f(u)du]u=ϕ(x)
定理1 设f(u)f(u)f(u)具有原函数,u=ϕ(x)u=\phi(x)u=ϕ(x)可导,则有换元公式
∫f[ϕ(x)]ϕ′(x)dx=[∫f(u)du]u=ϕ(x)\int{f[\phi(x)]\phi^{'}(x)dx}=[\int{f(u)du}]_{u=\phi(x)}∫f[ϕ(x)]ϕ′(x)dx=[∫f(u)du]u=ϕ(x)
1.2 例题
例1 求∫13+2xdx\int{\frac{1}{3+2x}dx}∫3+2x1dx
解:∫13+2xdx=12∫13+2xd(3+2x)=12ln∣3+2x∣+C解:\\ \int{\frac{1}{3+2x}dx}=\frac{1}{2}\int{\frac{1}{3+2x}d(3+2x)}=\frac{1}{2}\ln|3+2x|+C 解:∫3+2x1dx=21∫3+2x1d(3+2x)=21ln∣3+2x∣+C
例2 求∫x2(x+2)3dx\int{\frac{x^2}{(x+2)^3}dx}∫(x+2)3x2dx
注:分式积分,分母越简单越易积
解:令u=x+2,x=u−2∫x2(x+2)3dx=∫(u−2)2u3du=∫1udu−∫4u2du+∫4u3du=ln∣x+2∣+4x+2−12(x+2)2+C解:\\ 令u=x+2,x=u-2 \\ \int{\frac{x^2}{(x+2)^3}dx}=\int{\frac{(u-2)^2}{u^3}du}\\ =\int{\frac{1}{u}du}-\int{\frac{4}{u^2}du}+\int{\frac{4}{u^3}du}\\ =\ln|x+2|+\frac{4}{x+2}-\frac{1}{2(x+2)^2}+C 解:令u=x+2,x=u−2∫(x+2)3x2dx=∫u3(u−2)2du=∫u1du−∫u24du+∫u34du=ln∣x+2∣+x+24−2(x+2)21+C
例3 求∫1a2+x2dx\int{\frac{1}{a^2+x^2}dx}∫a2+x21dx
解析:基本积分公式∫11+x2dx=arctanx+C\int{\frac{1}{1+x^2}dx}=\arctan x+C∫1+x21dx=arctanx+C
解:∫1a2+x2dx=1a2∫11+(xa)2dx=1a∫11+(xa)2d(xa)=1aarctanxa+C解:\\ \int{\frac{1}{a^2+x^2}dx}=\frac{1}{a^2}\int{\frac{1}{1+(\frac{x}{a})^2}dx}\\ =\frac{1}{a}\int{\frac{1}{1+(\frac{x}{a})^2}d(\frac{x}{a})}=\frac{1}{a}\arctan\frac{x}{a}+C 解:∫a2+x21dx=a21∫1+(ax)21dx=a1∫1+(ax)21d(ax)=a1arctanax+C
例4 求∫1x2−a2dx\int{\frac{1}{x^2-a^2}dx}∫x2−a21dx
注:裂项公式,分母为两个一次项乘积形式1(x+a)(x+b)=1b−a(1x+a−1x+b)\frac{1}{(x+a)(x+b)}=\frac{1}{b-a}(\frac{1}{x+a}-\frac{1}{x+b})(x+a)(x+b)1=b−a1(x+a1−x+b1)
解:∫1x2−a2dx=12a[∫1x−ad(x−a)−∫1x+ad(x+a)]=12a(ln∣x−a∣−ln∣x+a∣)+C=12aln∣x−ax+a∣+C解:\\ \int{\frac{1}{x^2-a^2}dx}=\frac{1}{2a}[\int{\frac{1}{x-a}d(x-a)}-\int{\frac{1}{x+a}d(x+a)}]\\ =\frac{1}{2a}(\ln|x-a|-\ln|x+a|)+C=\frac{1}{2a}\ln|\frac{x-a}{x+a}|+C 解:∫x2−a21dx=2a1[∫x−a1d(x−a)−∫x+a1d(x+a)]=2a1(ln∣x−a∣−ln∣x+a∣)+C=2a1ln∣x+ax−a∣+C
例5 求∫dxx(1+2lnx)\int{\frac{dx}{x(1+2\ln x)}}∫x(1+2lnx)dx
解析:(lnx)′=1x(\ln x)^{'}=\frac{1}{x}(lnx)′=x1
解:∫dxx(1+2lnx)=12∫d(1+2lnx)1+2lnx=12ln∣1+2lnx∣+C解:\\ \int{\frac{dx}{x(1+2\ln x)}}=\frac{1}{2}\int{\frac{d(1+2\ln x)}{1+2\ln x}}\\ =\frac{1}{2}\ln|1+2\ln x|+C 解:∫x(1+2lnx)dx=21∫1+2lnxd(1+2lnx)=21ln∣1+2lnx∣+C
例6 求∫e3xxdx\int{\frac{e^{3\sqrt{x}}}{\sqrt{x}}dx}∫xe3xdx
解析:(x)′=12⋅1x(\sqrt{x})^{'}=\frac{1}{2}\cdot\frac{1}{\sqrt{x}}(x)′=21⋅x1
解:∫e3xxdx=23∫e3xd(3x)=23e3x+C解:\\ \int{\frac{e^{3\sqrt{x}}}{\sqrt{x}}dx}=\frac{2}{3}\int{e^{3\sqrt{x}}d(3\sqrt{x})}\\ =\frac{2}{3}e^{3\sqrt{x}}+C 解:∫xe3xdx=32∫e3xd(3x)=32e3x+C
例7 求∫sin2xcos5xdx\int{sin^2x\cos^5xdx}∫sin2xcos5xdx
解析:(sinx)′=cosx(cosx)′=−sinxsin2x+cos2x=1(\sin x)^{'}=\cos x\quad (\cos x)^{'}=-\sin x\quad \sin^2x+\cos^2x=1(sinx)′=cosx(cosx)′=−sinxsin2x+cos2x=1
解:∫sin2xcos5xdx=∫sin2xcos4xd(sinx)=∫sin2x(1−sin2x)2d(sinx)=∫(sin6x−2sin4x+sin2x)d(sinx)=17sin7x−25sin5x+13sin3x+C解:\int{sin^2x\cos^5xdx}=\int{sin^2x\cos^4xd(\sin x)}\\ =\int{sin^2x(1-\sin^2x)^2d(\sin x)}=\int{(\sin^6x-2\sin^4x+\sin^2x)d(\sin x)}\\ =\frac{1}{7}\sin^7x-\frac{2}{5}\sin^5x+\frac{1}{3}\sin^3x+C 解:∫sin2xcos5xdx=∫sin2xcos4xd(sinx)=∫sin2x(1−sin2x)2d(sinx)=∫(sin6x−2sin4x+sin2x)d(sinx)=71sin7x−52sin5x+31sin3x+C
一般地,对于sin2k+1xcosnx或sinnxcos2k+1x(其中k∈N)\sin^{2k+1}x\cos^nx或\sin^nx\cos^{2k+1}x(其中k\in N)sin2k+1xcosnx或sinnxcos2k+1x(其中k∈N)型函数的积分,总可依次做变换u=cosx或u=sinxu=\cos x或u=\sin xu=cosx或u=sinx,求得结果。
例8 求∫tanxdx\int{\tan xdx}∫tanxdx
解:∫tanxdx=∫sinxcosxdx=−∫1cosxd(cosx)=−ln∣cosx∣+C解:\int{\tan xdx}=\int{\frac{\sin x}{\cos x}dx}=-\int{\frac{1}{\cos x}d(\cos x)}\\ =-\ln|\cos x|+C 解:∫tanxdx=∫cosxsinxdx=−∫cosx1d(cosx)=−ln∣cosx∣+C
类似可得∫cotxdx=ln∣sinx∣+C\int{\cot xdx}=\ln|\sin x|+C∫cotxdx=ln∣sinx∣+C
例9 求∫x3(x2−2x+2)\int{\frac{x^3}{(x^2-2x+2)}}∫(x2−2x+2)x3
1.2 常见凑微分形式
1.2.1常见基本的导数公式的逆运算
- ∫f(1x)⋅1x2dx=−∫f(1x)d1x\int{f(\frac{1}{x})\cdot\frac{1}{x^2}dx}=-\int{f(\frac{1}{x})d\frac{1}{x}}∫f(x1)⋅x21dx=−∫f(x1)dx1
- ∫f(x)1xdx=2∫f(x)dx\int{f(\sqrt{x})\frac{1}{\sqrt{x}}dx}=2\int{f(\sqrt{x})d\sqrt{x}}∫f(x)x1dx=2∫f(x)dx
- ∫f(sinx)cosxdx=∫f(sinx)dsinx\int{f(\sin x)\cos xdx}=\int{f(\sin x)d\sin x}∫f(sinx)cosxdx=∫f(sinx)dsinx
- ∫f(cosx)sinxdx=−∫f(cosx)dcosx\int{f(\cos x)\sin xdx}=-\int{f(\cos x)d\cos x}∫f(cosx)sinxdx=−∫f(cosx)dcosx
- ∫f(lnx)1xdx=∫f(lnx)dlnx\int{f(\ln x)\frac{1}{x}dx}=\int{f(\ln x)d\ln x}∫f(lnx)x1dx=∫f(lnx)dlnx
- ∫f(xlnx)(1+lnx)dx=∫f(xlnx)d(xlnx)\int{f(x\ln x)(1+\ln x)dx}=\int{f(x\ln x)d(x\ln x)}∫f(xlnx)(1+lnx)dx=∫f(xlnx)d(xlnx)
- ∫f(secx)secxtanxdx=∫f(secx)dsecx\int{f(\sec x)\sec x\tan xdx}=\int{f(\sec x)d\sec x}∫f(secx)secxtanxdx=∫f(secx)dsecx
- ∫f(cscx)cscxcotxdx=−∫f(cscx)dcscx\int{f(\csc x)\csc x\cot xdx}=-\int{f(\csc x)d\csc x}∫f(cscx)cscxcotxdx=−∫f(cscx)dcscx
- ∫f(tanx)sec2xdx=∫f(tanx)dtanx\int{f(\tan x)\sec^2xdx}=\int{f(\tan x)d\tan x}∫f(tanx)sec2xdx=∫f(tanx)dtanx
- ∫f(cotx)csc2xdx=−∫f(cotx)dcotx\int{f(\cot x)\csc^2xdx}=-\int{f(\cot x)d\cot x}∫f(cotx)csc2xdx=−∫f(cotx)dcotx
- ∫f(arcsinx)11−x2dx=∫f(arcsinx)darcsinx\int{f(\arcsin x)\frac{1}{\sqrt{1-x^2}}dx}=\int{f(\arcsin x)d\arcsin x}∫f(arcsinx)1−x21dx=∫f(arcsinx)darcsinx
- ∫f(arctanx)11+x2dx=∫f(arcsinx)darctanx\int{f(\arctan x)\frac{1}{1+x^2}dx}=\int{f(\arcsin x)d\arctan x}∫f(arctanx)1+x21dx=∫f(arcsinx)darctanx
- ∫f(ex)exdx=∫f(ex)dex\int{f(e^x)e^xdx}=\int{f(e^x)de^x}∫f(ex)exdx=∫f(ex)dex
1.2.2被积函数含有三角函数
常用的三角恒等式:
- sin2x+cos2x=1\sin^2x+\cos^2x = 1sin2x+cos2x=1
- 1+tan2x=sec2x1+\tan^2x=\sec^2x1+tan2x=sec2x
- 1+cot2x=csc2x1+\cot^2x=\csc^2 x1+cot2x=csc2x
- 两角和差的三角公式
- cos(α±β)=cosαcosβ±sinαsinβ\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\pm\sin\alpha\sin\betacos(α±β)=cosαcosβ±sinαsinβ
- sin(α±β)=sinαcosβ±cosαsinβ\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\betasin(α±β)=sinαcosβ±cosαsinβ
- 2倍角公式,降幂公式
- cos2α=cos2α−sin2α=2cos2α−1=1−2sin2α\cos2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alphacos2α=cos2α−sin2α=2cos2α−1=1−2sin2α
- sin2α=2sinαcosα\sin2\alpha=2\sin\alpha\cos\alphasin2α=2sinαcosα
- cos2α=12(1+cos2α)\cos^2\alpha=\frac{1}{2}(1+\cos2\alpha)cos2α=21(1+cos2α)
- sin2α=12(1−cos2α)\sin^2\alpha=\frac{1}{2}(1-\cos2\alpha)sin2α=21(1−cos2α)
- 积化和差,和差化积

一般地,对于sin2k+1xcosnx或sinnxcos2k+1x(其中k∈N)\sin^{2k+1}x\cos^nx或\sin^nx\cos^{2k+1}x(其中k\in N)sin2k+1xcosnx或sinnxcos2k+1x(其中k∈N)型函数的积分,总可依次做变换u=cosx或u=sinxu=\cos x或u=\sin xu=cosx或u=sinx,求得结果。
tannxsec2kx或者tan2k−1xsecnx(n,k∈N+)\tan^nx\sec^{2k}x或者\tan^{2k-1}x\sec^nx(n,k\in N_+)tannxsec2kx或者tan2k−1xsecnx(n,k∈N+)型积分,可依次做变换u=tanx或u=secxu=\tan x或u=\sec xu=tanx或u=secx
2 第二类换元法
2.1 定理2
设x=ϕ(t)x=\phi(t)x=ϕ(t)是单调可导的函数,并且ϕ′(t)≠0.又设f[ϕ(t)]ϕ′(t)\phi^{'}(t)\not=0.又设f[\phi(t)]\phi^{'}(t)ϕ′(t)=0.又设f[ϕ(t)]ϕ′(t)具有原函数,则有换元公式
∫f(x)dx=[∫f[ϕ(t)]ϕ′(t)dt]t=ϕ−1(x)\int{f(x)dx}=[\int{f[\phi(t)]\phi^{'}(t)dt}]_{t=\phi^{-1}(x)}∫f(x)dx=[∫f[ϕ(t)]ϕ′(t)dt]t=ϕ−1(x)
其中ϕ−1(x)是x=ϕ(t)\phi^{-1}(x)是x=\phi(t)ϕ−1(x)是x=ϕ(t)的反函数。
证明:设f[ϕ(t)]ϕ′(t)的原函数为Φ(t),记Φ(t)=Φ[ϕ−1(x)]=F(x)利用复合函数和反函数的求导法则,有F′(x)=dΦdt⋅dtdx=f[ϕ(t)]ϕ′(t)⋅1ϕ′(t)=f(x)即F(x)是f(x)的原函数,所以有∫f(x)dx=F(x)+c=Φ[ϕ−1(x)]+C=[∫f[ϕ(t)]ϕ′(t)dt]t=ϕ−1(x)证明:\\ 设f[\phi(t)]\phi^{'}(t)的原函数为\Phi(t),记\Phi(t)=\Phi[\phi^{-1}(x)]=F(x)\\ 利用复合函数和反函数的求导法则,有\\ F^{'}(x)=\frac{d\Phi}{dt}\cdot\frac{dt}{dx}=f[\phi(t)]\phi^{'}(t)\cdot\frac{1}{\phi^{'}(t)}=f(x) \\ 即F(x)是f(x)的原函数,所以有 \\ \int{f(x)dx}=F(x)+c=\Phi[\phi^{-1}(x)]+C=[\int{f[\phi(t)]\phi^{'}(t)dt}]_{t=\phi^{-1}(x)} 证明:设f[ϕ(t)]ϕ′(t)的原函数为Φ(t),记Φ(t)=Φ[ϕ−1(x)]=F(x)利用复合函数和反函数的求导法则,有F′(x)=dtdΦ⋅dxdt=f[ϕ(t)]ϕ′(t)⋅ϕ′(t)1=f(x)即F(x)是f(x)的原函数,所以有∫f(x)dx=F(x)+c=Φ[ϕ−1(x)]+C=[∫f[ϕ(t)]ϕ′(t)dt]t=ϕ−1(x)
注:
- 必须写出变量代换x=ϕ(t)x=\phi(t)x=ϕ(t)
- 必须替换微分dx=ϕ′(t)dtdx=\phi^{'}(t)dtdx=ϕ′(t)dt
- 最后结果必须还原成原来积分变量t=ϕ−1(x)t=\phi^{-1}(x)t=ϕ−1(x)
2.2 常见第二换元代换方法
- 三角代换
- 倒代换
- 根式代换
2.2.1 三角代换-弦代换
正弦或者余弦代换
例1 求∫a2−x2dx(a>0)\int{\sqrt{a^2-x^2}dx}(a\gt0)∫a2−x2dx(a>0)
解:令x=asint,−π2<t<π2a2−x2=acost,dx=acostdt∫a2−x2dx=∫acost⋅acostdt=a22t+a24sin2t+C=a22t+a22sintcost+C其中t=arcsinxa,sint=xa,cost=a2−x2a∫a2−x2dx=a22arcsinxa+xa2−x22+C解:令x=a\sin t,-\frac{\pi}{2}\lt t\lt\frac{\pi}{2}\\ \sqrt{a^2-x^2}=a\cos t,dx=a\cos tdt \\ \int{\sqrt{a^2-x^2}dx}=\int{a\cos t\cdot a\cos tdt}=\frac{a^2}{2}t+\frac{a^2}{4}\sin2t+C\\ =\frac{a^2}{2}t+\frac{a^2}{2}\sin t\cos t+C\\ 其中t=\arcsin\frac{x}{a},\sin t=\frac{x}{a},\cos t=\frac{\sqrt{a^2-x^2}}{a}\\ \int{\sqrt{a^2-x^2}dx}=\frac{a^2}{2}\arcsin\frac{x}{a}+\frac{x\sqrt{a^2-x^2}}{2}+C 解:令x=asint,−2π<t<2πa2−x2=acost,dx=acostdt∫a2−x2dx=∫acost⋅acostdt=2a2t+4a2sin2t+C=2a2t+2a2sintcost+C其中t=arcsinax,sint=ax,cost=aa2−x2∫a2−x2dx=2a2arcsinax+2xa2−x2+C
2.2.2 三角代换-切代换
正切或者余切
例2 求∫1x2+a2dx(a>0)\int{\frac{1}{\sqrt{x^2+a^2}}dx}(a>0)∫x2+a21dx(a>0)
解:令x=atant,−π2<t<π2x2+a2=asect,dx=asec2t∫1x2+a2dx=∫1asect⋅asec2tdt=∫sectdt=ln∣sect+tant∣+C其中tant=xa,sect=x2+a2a∫1x2+a2dx=ln∣x2+a2a+xa∣+C1=ln(x2+a2+x)+C解:令x=a\tan t,-\frac{\pi}{2}\lt t\lt\frac{\pi}{2} \\ \sqrt{x^2+a^2}=a\sec t,dx=asec^2t \\ \int{\frac{1}{\sqrt{x^2+a^2}}dx}=\int{\frac{1}{a\sec t}\cdot a\sec^2tdt}\\ =\int{\sec tdt}=\ln|\sec t+\tan t|+C \\ 其中\tan t=\frac{x}{a},\sec t=\frac{\sqrt{x^2+a^2}}{a} \\ \int{\frac{1}{\sqrt{x^2+a^2}}dx}=\ln|\frac{\sqrt{x^2+a^2}}{a}+\frac{x}{a}|+C_1\\ =ln(\sqrt{x^2+a^2}+x)+C 解:令x=atant,−2π<t<2πx2+a2=asect,dx=asec2t∫x2+a21dx=∫asect1⋅asec2tdt=∫sectdt=ln∣sect+tant∣+C其中tant=ax,sect=ax2+a2∫x2+a21dx=ln∣ax2+a2+ax∣+C1=ln(x2+a2+x)+C
2.2.3 三角代换-割代换
正割或者余割
例3 求∫1x2−a2dx(a>0)\int{\frac{1}{\sqrt{x^2-a^2}}dx}(a\gt0)∫x2−a21dx(a>0)
解:定义域x>a或者x<−a(1)当x>a时,令x=asect,0<t<π2x2−a2=atant,dx=asecttantdt∫1x2−a2dx=∫1atantasecttantdt=∫sectdt=ln∣sect+tant∣+C1其中sect=xa,tant=x2−a2a∫1x2−a2dx=ln(x+x2−a2)+C(2)当x<−a时,令u=−x,则u>a∫1x2−a2dx=−∫1u2−a2du=−ln(u+u2−a2)+C=−ln(−x+x2−a2)+C=ln(−x−x2−a2)+C1综上当x>a时,∫1x2−a2dx=ln(x+x−a2)+Cx<−a时,∫1x2−a2dx=ln(−x−x2−a2)+C所以∫1x2−a2dx=ln∣x+x2−a2∣+C解:定义域x\gt a或者x\lt -a \\ (1)当x\gt a时,令x=a\sec t,0\lt t\lt\frac{\pi}{2} \\ \sqrt{x^2-a^2}=a\tan t,dx=a\sec t\tan tdt \\ \int{\frac{1}{\sqrt{x^2-a^2}}dx}=\int{\frac{1}{a\tan t}a\sec t\tan tdt}\\ =\int{\sec tdt}=\ln|\sec t+\tan t|+C_1 \\ 其中\sec t=\frac{x}{a},\tan t=\frac{\sqrt{x^2-a^2}}{a} \\ \int{\frac{1}{\sqrt{x^2-a^2}}dx}=\ln(x+\sqrt{x^2-a^2})+C \\ (2)当x\lt -a时,令u=-x,则u\gt a \\ \int{\frac{1}{\sqrt{x^2-a^2}}dx}=-\int{\frac{1}{\sqrt{u^2-a^2}}du}\\ =-\ln(u+\sqrt{u^2-a^2})+C=-\ln(-x+\sqrt{x^2-a^2})+C=\ln(-x-\sqrt{x^2-a^2})+C_1\\ 综上当x\gt a时,\int{\frac{1}{\sqrt{x^2-a^2}}dx}=\ln(x+\sqrt{x^-a^2})+C \\ x\lt -a时,\int{\frac{1}{\sqrt{x^2-a^2}}dx}=\ln(-x-\sqrt{x^2-a^2})+C\\ 所以\int{\frac{1}{\sqrt{x^2-a^2}}dx}=\ln|x+\sqrt{x^2-a^2}|+C 解:定义域x>a或者x<−a(1)当x>a时,令x=asect,0<t<2πx2−a2=atant,dx=asecttantdt∫x2−a21dx=∫atant1asecttantdt=∫sectdt=ln∣sect+tant∣+C1其中sect=ax,tant=ax2−a2∫x2−a21dx=ln(x+x2−a2)+C(2)当x<−a时,令u=−x,则u>a∫x2−a21dx=−∫u2−a21du=−ln(u+u2−a2)+C=−ln(−x+x2−a2)+C=ln(−x−x2−a2)+C1综上当x>a时,∫x2−a21dx=ln(x+x−a2)+Cx<−a时,∫x2−a21dx=ln(−x−x2−a2)+C所以∫x2−a21dx=ln∣x+x2−a2∣+C
2.2.4 三角代换汇总
| 被积函数中函数含有 | 三角代换 |
|---|---|
| a2−x2\sqrt{a^2-x^2}a2−x2 | x=asint,−π2<t<π2x=a\sin t,-\frac{\pi}{2}\lt t\lt \frac{\pi}{2}x=asint,−2π<t<2π |
| a2+x2\sqrt{a^2+x^2}a2+x2 | x=atant,−π2<t<π2x=a\tan t,-\frac{\pi}{2}\lt t\lt \frac{\pi}{2}x=atant,−2π<t<2π |
| x2−a2\sqrt{x^2-a^2}x2−a2 | x>a,x=asect,0<t<π2x\gt a,x=a\sec t,0\lt t\lt \frac{\pi}{2}x>a,x=asect,0<t<2π |
2.2.5 倒代换
适用:分母次数>分子次数
例4 求∫a2−x2x4dx(a≠0)\int{\frac{\sqrt{a^2-x^2}}{x^4}dx}(a\not=0)∫x4a2−x2dx(a=0)
解:(1)利用上面的三角代换,自己做(1)倒代换,令x=1tdx=−1t2,a2−x2=a2t2−1∣t∣∫a2−x2x4dx=∫a2t2−1∣t∣⋅t4⋅(−1t2)dt=−∫a2t2−1⋅∣t∣dt当x>0时,t=1x>0∫a2−x2x4dx=−12a2∫(a2t2−1)12d(a2t2−1)dt=−(a2−x2)323a2x3+C当x<0时,t=1x<0∫a2−x2x4dx=−(a2−x2)323a2x3+C综上∫a2−x2x4dx=−(a2−x2)323a2x3+C解:(1)利用上面的三角代换,自己做\\ (1)倒代换,令x=\frac{1}{t} \\ dx=-\frac{1}{t^2},\sqrt{a^2-x^2}=\frac{\sqrt{a^2t^2-1}}{|t|} \\ \int{\frac{\sqrt{a^2-x^2}}{x^4}dx}=\int{\frac{\sqrt{a^2t^2-1}}{|t|}\cdot t^4\cdot(-\frac{1}{t^2})dt} \\ =-\int{\sqrt{a^2t^2-1}\cdot|t|dt} \\ 当x\gt0时,t=\frac{1}{x}\gt0\\ \int{\frac{\sqrt{a^2-x^2}}{x^4}dx}=-\frac{1}{2a^2}\int{(a^2t^2-1)^{\frac{1}{2}}d(a^2t^2-1)dt}=-\frac{(a^2-x^2)^{\frac{3}{2}}}{3a^2x^3}+C\\ 当x\lt0时,t=\frac{1}{x}\lt0\\ \int{\frac{\sqrt{a^2-x^2}}{x^4}dx}=-\frac{(a^2-x^2)^{\frac{3}{2}}}{3a^2x^3}+C \\ 综上 \int{\frac{\sqrt{a^2-x^2}}{x^4}dx}=-\frac{(a^2-x^2)^{\frac{3}{2}}}{3a^2x^3}+C 解:(1)利用上面的三角代换,自己做(1)倒代换,令x=t1dx=−t21,a2−x2=∣t∣a2t2−1∫x4a2−x2dx=∫∣t∣a2t2−1⋅t4⋅(−t21)dt=−∫a2t2−1⋅∣t∣dt当x>0时,t=x1>0∫x4a2−x2dx=−2a21∫(a2t2−1)21d(a2t2−1)dt=−3a2x3(a2−x2)23+C当x<0时,t=x1<0∫x4a2−x2dx=−3a2x3(a2−x2)23+C综上∫x4a2−x2dx=−3a2x3(a2−x2)23+C
2.2.6 根式代换
例5 求∫11+2xdx\int{\frac{1}{1+\sqrt{2x}}dx}∫1+2x1dx
解:令2x=t,x=t22,dx=t∫11+2xdx=∫t1+tdt=t−ln∣t+1∣+C=2x−ln∣sqrt2x+1∣+C解:令\sqrt{2x}=t,x=\frac{t^2}{2},dx=t \\ \int{\frac{1}{1+\sqrt{2x}}dx}=\int{\frac{t}{1+t}dt}=t-\ln|t+1|+C\\ =\sqrt{2x}-\ln|sqrt{2x}+1|+C 解:令2x=t,x=2t2,dx=t∫1+2x1dx=∫1+ttdt=t−ln∣t+1∣+C=2x−ln∣sqrt2x+1∣+C
3 积分推导公式
常用积分公式,除了基本积分表中,在添加下面几个前面推导的公式:
- ∫tanxdx=−ln∣cosx∣+C\int{\tan xdx}=-\ln|\cos x|+C∫tanxdx=−ln∣cosx∣+C
- ∫cotxdx=ln∣sinx∣+C\int{\cot xdx}=\ln|\sin x|+C∫cotxdx=ln∣sinx∣+C
- ∫secxdx=ln∣secx+tanx∣+C\int{\sec xdx}=\ln|\sec x+\tan x|+C∫secxdx=ln∣secx+tanx∣+C
- ∫cscxdx=ln∣cscx−cotx∣+C\int{\csc xdx}=\ln|\csc x-\cot x|+C∫cscxdx=ln∣cscx−cotx∣+C
- ∫1a2+x2dx=1aarctanxa+C\int{\frac{1}{a^2+x^2}dx}=\frac{1}{a}\arctan\frac{x}{a}+C∫a2+x21dx=a1arctanax+C
- ∫dxx2−a2=12aln∣x−ax+a∣+C\int{\frac{dx}{x^2-a^2}}=\frac{1}{2a}\ln|\frac{x-a}{x+a}|+C∫x2−a2dx=2a1ln∣x+ax−a∣+C
- ∫dxa2−x2=arcsinxa+C\int{\frac{dx}{\sqrt{a^2-x^2}}}=\arcsin\frac{x}{a}+C∫a2−x2dx=arcsinax+C
- ∫dxx2+a2=ln(x+x2+a2)+C\int{\frac{dx}{\sqrt{x^2+a^2}}}=\ln(x+\sqrt{x^2+a^2})+C∫x2+a2dx=ln(x+x2+a2)+C
- ∫dxx2−a2=ln∣x+x2−a2∣+C\int{\frac{dx}{\sqrt{x^2-a^2}}}=\ln|x+\sqrt{x^2-a^2}|+C∫x2−a2dx=ln∣x+x2−a2∣+C
例6 求 ∫x3(x2−2x+2)2dx\int{\frac{x^3}{(x^2-2x+2)^2}dx}∫(x2−2x+2)2x3dx
解:x2−2x+2=(x−1)2+1,令x−1=tant,(−π2<t<π2)∫x3(x2−2x+2)2dx=∫(tant+1)3sec4tsec2tdt=∫(sin3tcos−1t+3sin2t+3sintcost+cos2t)dt=−lncost−cos2t+2t−sintcost+C按tant=x−1做辅助三角形,cost=1x2−2x+2,sint=x−1x2−2x+2∫x3(x2−2x+2)2dx=12ln(x2−2x+2)+2arctan(x−1)−xx2−2x+2+C解:\\ x^2-2x+2=(x-1)^2+1 ,令x-1=\tan t ,(-\frac{\pi}{2}\lt t\lt\frac{\pi}{2})\\ \int{\frac{x^3}{(x^2-2x+2)^2}dx}=\int{\frac{(\tan t+1)^3}{\sec^4t}\sec^2tdt}\\ =\int{(\sin^3t\cos^{-1}t+3\sin^2t+3\sin t\cos t+\cos^2t)dt}\\ =-\ln\cos t-\cos^2t+2t-\sin t\cos t+C\\ 按\tan t=x-1做辅助三角形,\\ \cos t=\frac{1}{\sqrt{x^2-2x+2}},\sin t=\frac{x-1}{\sqrt{x^2-2x+2}} \\ \int{\frac{x^3}{(x^2-2x+2)^2}dx}=\frac{1}{2}\ln(x^2-2x+2)+2\arctan(x-1)-\frac{x}{x^2-2x+2}+C 解:x2−2x+2=(x−1)2+1,令x−1=tant,(−2π<t<2π)∫(x2−2x+2)2x3dx=∫sec4t(tant+1)3sec2tdt=∫(sin3tcos−1t+3sin2t+3sintcost+cos2t)dt=−lncost−cos2t+2t−sintcost+C按tant=x−1做辅助三角形,cost=x2−2x+21,sint=x2−2x+2x−1∫(x2−2x+2)2x3dx=21ln(x2−2x+2)+2arctan(x−1)−x2−2x+2x+C
辅助三角形图示:
后记
❓QQ:806797785
⭐️文档笔记地址:https://gitee.com/gaogzhen/math
参考:
[1]同济大学数学系.高等数学 第七版 上册[M].北京:高等教育出版社,2014.7.P193~p207.
[2]【梨米特】同济七版《高等数学》全程教学视频|纯干货知识点解析,应该是全网最细|微积分 | 高数[CP/OL].2020-04-16.p28.
- 三角函数公式
相关文章:

0402换元积分法-不定积分
文章目录1 第一类换元法1.1 定理11.2 例题1.2 常见凑微分形式1.2.1常见基本的导数公式的逆运算1.2.2被积函数含有三角函数2 第二类换元法2.1 定理22.2 常见第二换元代换方法2.2.1 三角代换-弦代换2.2.2 三角代换-切代换2.2.3 三角代换-割代换2.2.4 三角代换汇总2.2.5 倒代换2.2…...
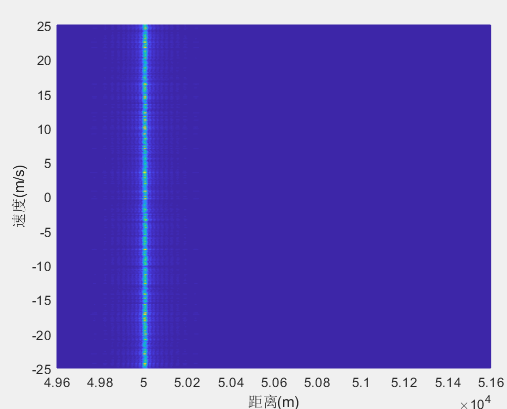
信号类型(雷达)——脉冲雷达(三)
系列文章目录 《信号类型(雷达通信)》 《信号类型(雷达)——雷达波形认识(一)》 《信号类型(雷达)——连续波雷达(二)》 文章目录 前言 一、相参雷达 1…...
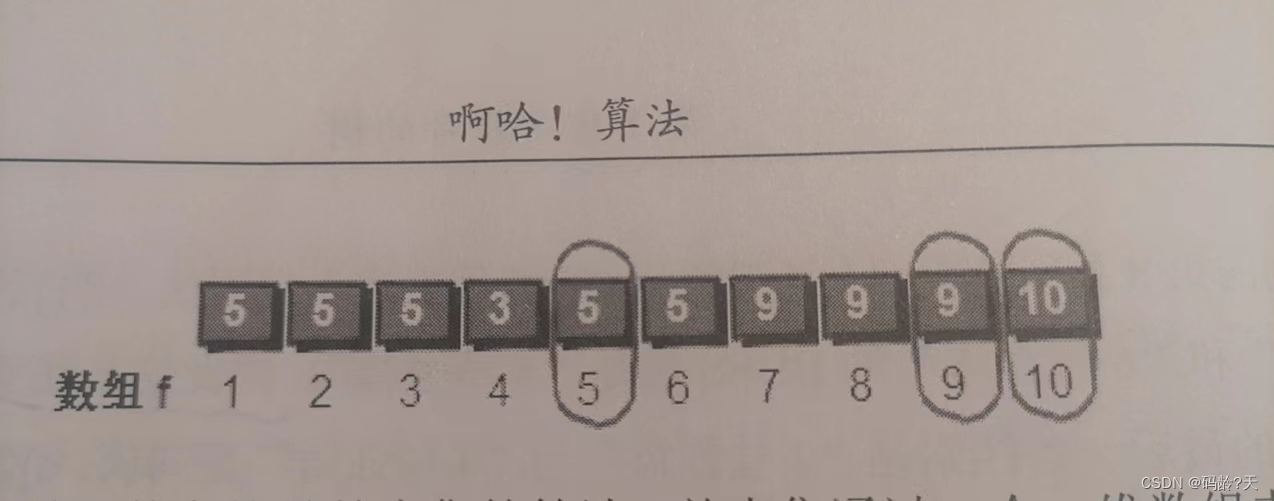
并查集(13张图解)--擒贼先擒王
目录 前言 故事 🌼思路 🌼总结 🌼代码 👊观察过程代码 👊正确代码 👊细节代码 来自《啊哈算法》 前言 刚学了树在优先队列中的应用--堆的实现 那么树还有哪些神奇的用法呢?我们从一…...
Flutter3引用原生播放器-IOS(Swift)篇
前言由于Flutter项目中需要使用到播放器功能,因此对flutter中各种播放器解决方案进行了一番研究和比对,最后决定还是自己通过Plugin的方法去引用原生播放器符合自己的需求,本篇文章会对各种解决方案做一个简单的比较,以及讲解一下…...
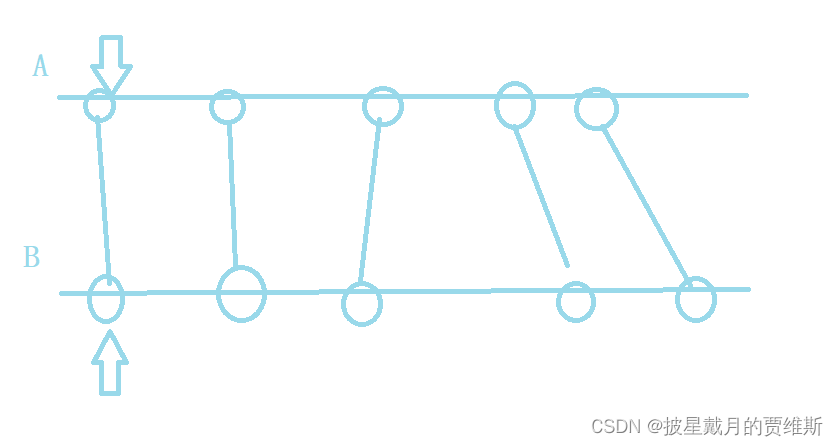
【蓝桥杯每日一题】双指针算法
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙我与杀戮之中绽放,亦如黎明的花…...
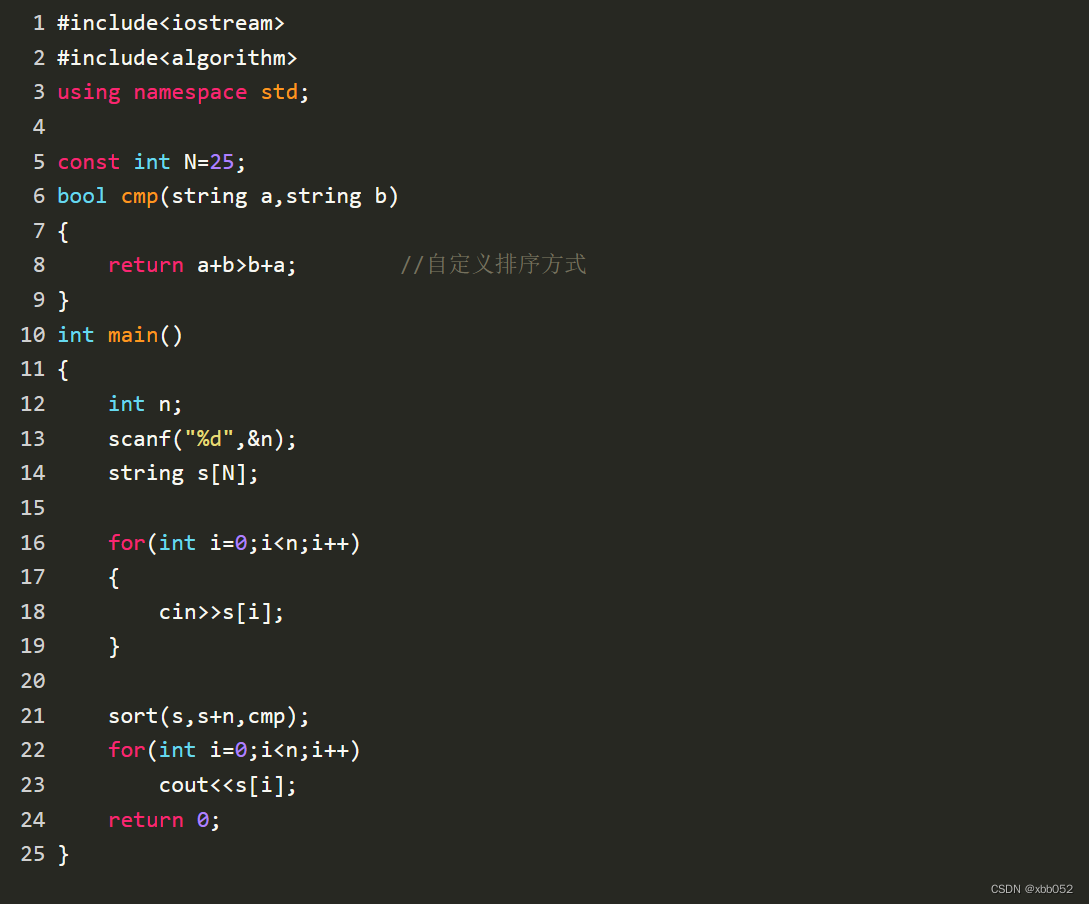
拼数(一般贪心)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题号:NC16783 时间限制:C/C 1秒,其他语言2秒 空间限制:C/C 262144K,其他语言524288K 64bit IO Format: %lld 题目描述 设有n个正整…...

LeetCode 热题 C++ 169. 多数元素 10. 正则表达式匹配 155. 最小栈
力扣169 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输出࿱…...
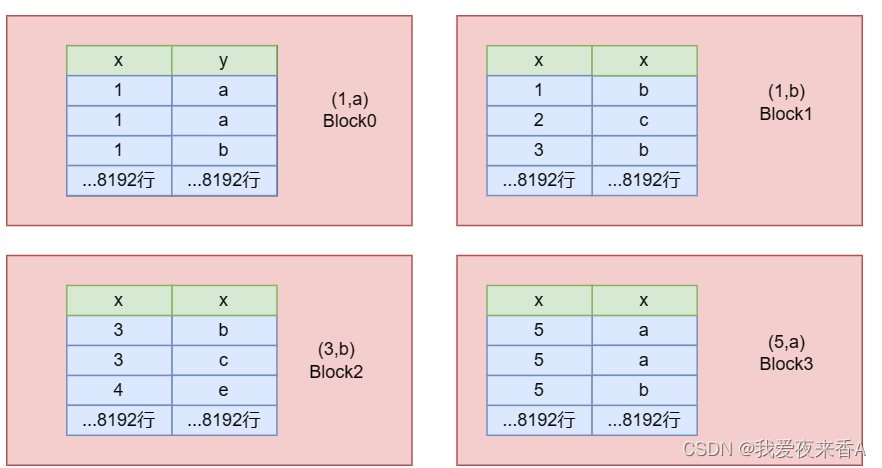
Clickhouse学习:MergeTree
MergeTree一、MergeTree逻辑存储结构二、MergeTree物理存储结构三、总结一、MergeTree逻辑存储结构 如上图所示,在排序键(CountrID、Date)上做索引,数据会按照这两个字段先后排序ClickHouse是稀疏索引,每隔8192行做一个索引,如(a,1),(a,2),比如想查a,要读取[0,3)之间的内容,稀疏…...
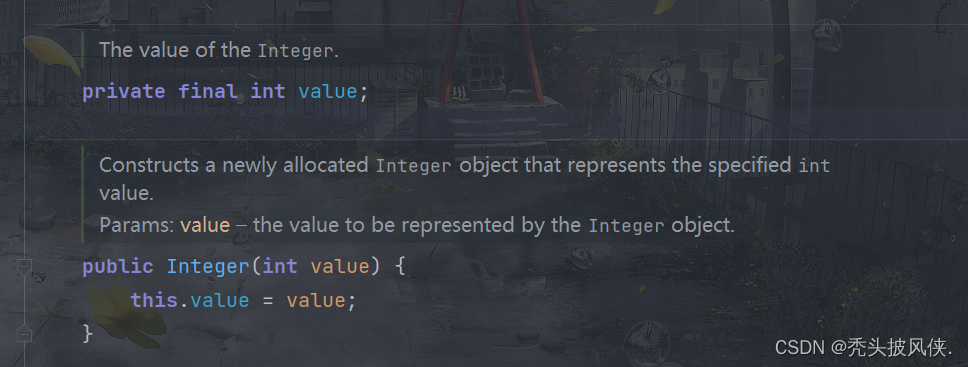
【java基础】包装类,自动装箱和自动拆箱
文章目录基本介绍包装类自动装箱自动拆箱包装类注意事项包装类比较包装器内容不可变基本介绍 有时,需要将int这样的基本类型转换为对象。所有的基本类型都有一个与之对应的类。 例如,Integer类对应基本类型int。通常,这些类称为包装器&#…...
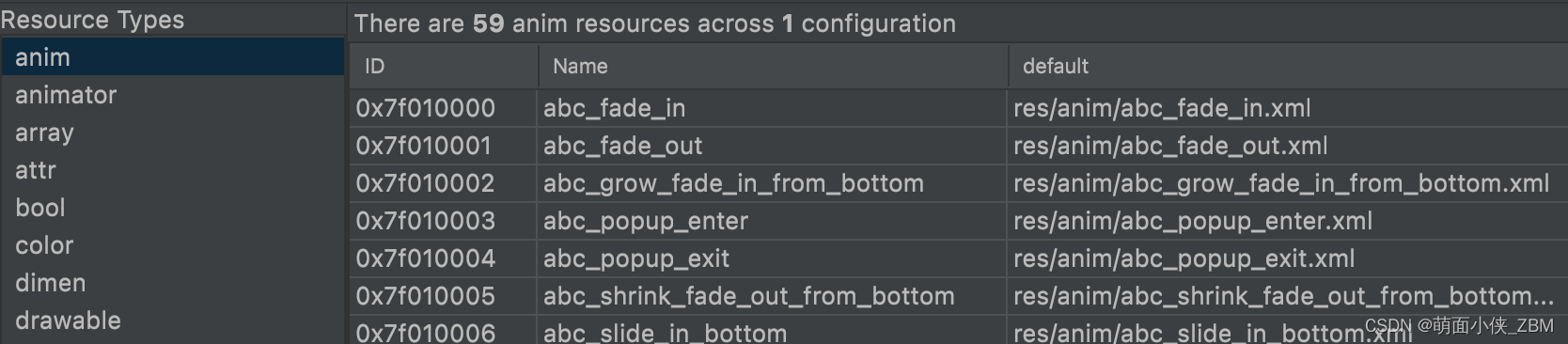
Android笔记(二十五):两种sdk热更插件资源加载方案
背景 在研究sdk插件化热更新方式的过程中总结出了两套插件资源加载方案,在此记录下 资源热更方式 方式一:合并所有插件资源 需要解决资源id冲突问题 资源ID值一共4个字段,由三部分组成:PackageIdTypeIdEntryId PackageId&…...

spring框架--全面详解(学习笔记)
目录 1.Spring是什么 2.Spring 框架特点 3.Spring体系结构 4.Spring开发环境搭建 5.spring中IOC和DI 6.Spring中bean的生命周期 7.Spring Bean作用域 8.spring注解开发 9.Spring框架中AOP(Aspect Oriented Programming) 10.AOP 实现分类 11.A…...
)
2023年CDGA考试模拟题库(401-500)
2023年CDGA考试模拟题库(401-500) 401.数据管理战略的SMART原则指的是哪项? [1分] A.具体 、高质量、可操作 、现实、有时间限制 B.具体、可衡量、可检验、现实、有时间限制 C.具体、可衡量、可操作、现实、有时间限制 D.具体、高质量、可检验、现实12-24个月的目标 答…...

软件设计师备考文档
cpu 计算机的基本硬件系统:运算器、控制器、存储器、输入设备、输出设备 cpu负责获取程序指令,对指令进行译码并加以执行 * cpu的功能控制器(保证程序正常执行,处理异常事件) 程序控制操作控制运算器(只能…...
)
Javascript的API基本内容(一)
一、获取DOM对象 querySelector 满足条件的第一个元素 querySelectorAll 满足条件的元素集合 返回伪数组 document.getElementById 专门获取元素类型节点,根据标签的 id 属性查找 二、操作元素内容 通过修改 DOM 的文本内容,动态改变网页的内容。 inn…...

10、最小公倍数
法一: #include <stdio.h>int main(){int a,b;scanf("%d%d",&a,&b);int m a>b?a:b;//m表示a,b之间的较大值while(1){if(m%a0&&m%b0){break;}m;}printf("%d",m);return 0; }法二:a*i%b0成立 #include &…...

【vue】vue2.x项目中使用md文件
一、Vue项目展示md文件的三种方式 1、将md文件 导入为 html 生成的标题标签自带具有id属性,值为标题内容; <h2 id"测试">测试</h2> # 处理md为html字符串 yarn add markdown-loader # 处理字符串,用于导出显示 yarn a…...

操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 注:阅读本编文章前,请先阅读系列文章,以免造成看不懂的情况!! MSF和CS绕过UAC提权 CS绕过UAC提权 拿到一个普通管理员的SHELL,在CS中没有*号代表有…...

快速排序+快速定位
快速排序算法采用了分治法以及递归作为解决问题的思想。在计算机科学中,分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以…...

nginx http rewrite module 详解
大家好,我是 17。 今天和大家聊聊 nginx http rewrite module 。 简单来说, ngx_http_rewrite_module module 用正则匹配请求,改写请求,然后做跳转。可以是内部跳转,也可以是外部跳转。 学习这个模块的时候…...

机器学习可解释性一(LIME)
随着深度学习的发展,越来越多的模型诞生,并且在训练集和测试集上的表现甚至于高于人类,但是深度学习一直被认为是一个黑盒模型,我们通俗的认为,经过训练后,机器学习到了数据中的特征,进而可以正…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
