赛后补题:CF1789C Serval and Toxel‘s Arrays
传送门:CF
题目描述:
题目较长,此处省略
输入:
3
3 2
1 2 3
1 4
2 5
1 1
1
1 1
10 10
4 6 9 12 16 20 2 10 19 7
1 3
5 4
2 17
2 18
6 11
7 1
8 17
5 5
5 5
2 2
输出:
13
1
705
比赛的时候感觉已经想到了正解,但是没有想的很清楚,所以赛时没有打出来.
我认为这道题的突破口其实是在ai<=n+ma_i<=n+mai<=n+m这里的.有了这个,所以我们最终的算法能够不是n2n^2n2,但是赛时我甚至没有注意到这一点(笑
对于每一个数组中的一个数字来说,我们考虑计算这个数字在其他所有数组中的贡献.我们会发现当这个数字不在其他数组中的时候,显然我们可以得到一个贡献,但是当我们的这个数字在其他数组中的时候,我们此时的这个数字在这个数组中是没有贡献的.我们可以先假装这个数字在其他数组中是没有的,那么此时我们的总贡献就是m∗(1+m)/2m*(1+m)/2m∗(1+m)/2(一共有m+1个数组).但是我们此时可能有一种情况就是有重复数字的贡献,所以我们考虑将这个重复数字的贡献减掉.我们可以计算出在所有m+1m+1m+1个数组中这个数字的个数cntcntcnt,那么对于所有的数组来说,我们之前所重复计算的就是cnt∗(cnt−1)cnt*(cnt-1)cnt∗(cnt−1)[也就是这cnt个数组两两配对的个数],那么此时我们的这个数字的总贡献就是m∗(m+1)/2−cnt∗(cnt−1)m*(m+1)/2-cnt*(cnt-1)m∗(m+1)/2−cnt∗(cnt−1)
所以我们此时的问题就变成了如何计算出这么多的数组里面每一个数字的个数.每一次更改时,我们可以使用lastlastlast数组来记录上一次该数字出现的位置,然后计算一下这个数字知道消失所存在的数组此处即可.并且需要注意的我们还需要累计每一个数字一直到最后的存在的次数
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int T;int n;int m;int last[maxn];
int a[maxn];int cnt[maxn];
void init() {for(int i=1;i<=n+m;i++) {last[i]=-1;cnt[i]=0;}
}
signed main() {T=read();while(T--) {n=read();m=read();init();for(int i=1;i<=n;i++){a[i]=read();last[a[i]]=0;} for(int i=1;i<=m;i++) {int pos=read(),val=read();cnt[a[pos]]+=i-last[a[pos]];last[a[pos]]=-1;last[val]=i;a[pos]=val;}for(int i=1;i<=n+m;i++) {if(last[i]!=-1) {cnt[i]+=(m+1-last[i]);}}ll ans=2*n*(m+1)*(m)/2;for(int i=1;i<=n+m;i++) {ans-=cnt[i]*(cnt[i]-1)/2;}printf("%lld\n",ans);}return 0;
}
相关文章:

赛后补题:CF1789C Serval and Toxel‘s Arrays
传送门:CF 题目描述: 题目较长,此处省略 输入: 3 3 2 1 2 3 1 4 2 5 1 1 1 1 1 10 10 4 6 9 12 16 20 2 10 19 7 1 3 5 4 2 17 2 18 6 11 7 1 8 17 5 5 5 5 2 2 输出: 13 1 705比赛的时候感觉已经想到了正解,但是没有想的很清楚,所以赛时没有打出来. 我认为这道题的突破口其…...

Linux学习(8.7)命令与文件的搜寻
目录 命令与文件的搜寻 which 文件档名的搜寻: whereis (寻找特定文件) locate find 以下内容转载自鸟哥的Linux私房菜 命令与文件的搜寻 which 这个命令是根据『PATH』这个环境变量所规范的路径,去搜寻『运行档』的档名~ 所以&am…...

Linux下 Makefile文件基本语法二
本文继续上一篇关于 Makefile 文件内容的介绍。上一篇文章如下: Linux下 Makefile 基本语法_凌雪舞的博客-CSDN博客 一. Makefile 上一篇文章介绍了 Makefile基本语法中的变量,模式规则,自动化变量。这里继续介绍 Makefile 的另外一些语…...
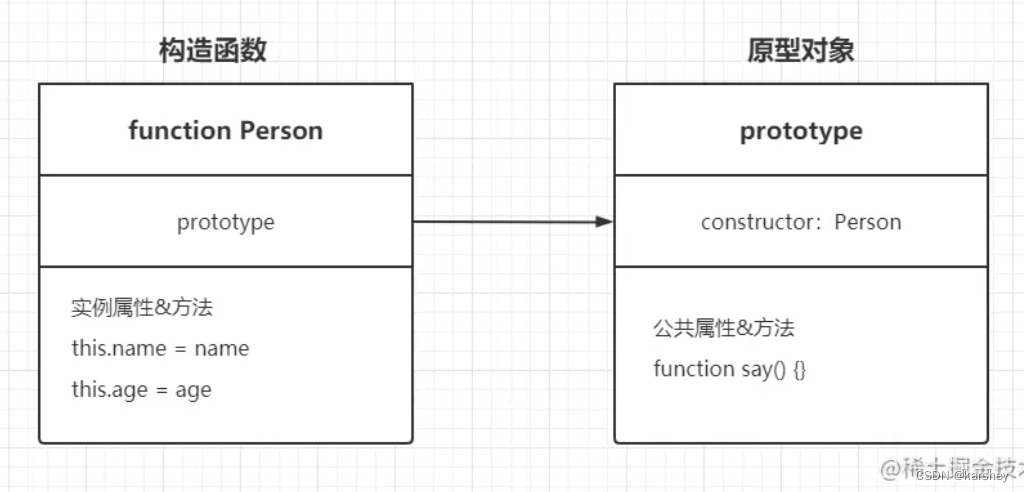
【前端】JavaScript构造函数
文章目录概念执行过程返回值原型与constructor继承方式原型链其他继承方式(还没写)参考概念 在JS中,通过new来实例化对象的函数叫构造函数。实例化对象,也就是初始化一个实例对象。构造函数一般首字母大写。 构造函数的目的&…...

STM32单片机之温湿度检测系统(DTH11、OLED、LCD1602)
LCD1602LCD1602引脚第 1 脚: VSS 为电源地 第 2 脚: VDD 接 5V 正电源 第 3 脚: VL 为液晶显示器对比度调整端,接正电源时对比度最弱,接地时对比度最高,对比度过高时会产生“鬼影”,使用时可以通过一个 10K 的电位器调整对比度。 第 4 脚&…...

vitepress 就这几步操作,博客就搭好啦?
Ⅰ、什么是vitepress 💎 vitepress 使用场景 简单的说 ,只要 会用 markdown 语法,就能构建自己的 「博客、笔记、使用文档」等系统 ; ✨ vitepress 优势 优势介绍傻瓜式操作只需要配置 菜单 和 对应的 markdown 就能实现博客、笔…...
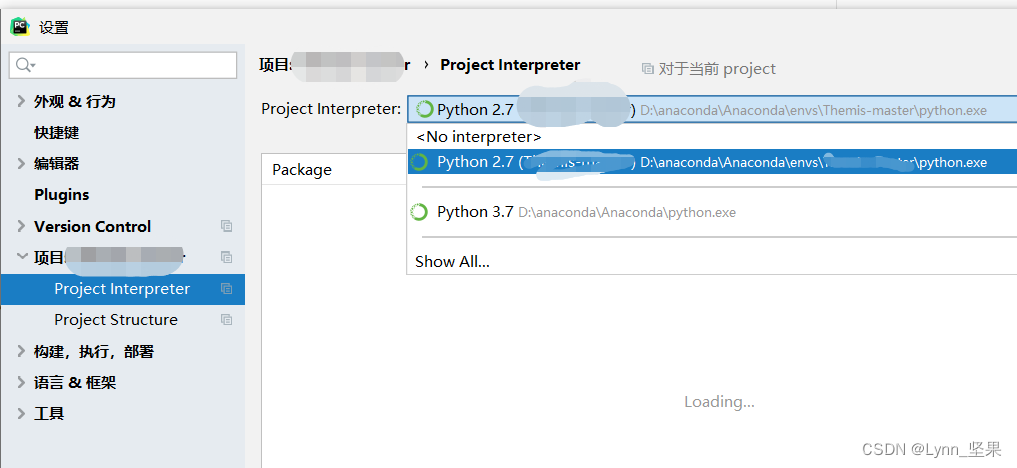
【Python工具篇】Anaconda中安装python2和python3以及在pycharm中使用
背景:已经安装好anaconda、python3、pycharm,因为项目使用的是python2语法,所以需要在anaconda中安装python2,并在pycharm中使用,下面给出步骤。 1. 打开cmd或者是Anaconda Prompt。 下面是anaconda prompt. 2. 查…...

Android 网络框架——Retrofit源码精析
众所周知,Retrofit是OkHttp的封装,APP对网络交互部分的实现基本上都是RxJavaRetrofitOkHttp架构(或协程RetrofitOkHttp),可以说,Retrofit已经广为人知。本文主要介绍Retrofit主线源码实现机制,及…...
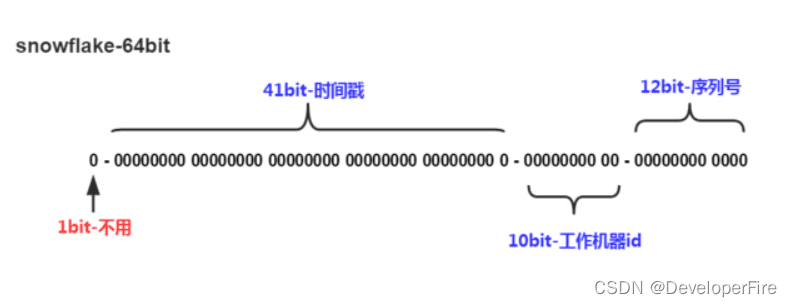
分布式算法 - Snowflake算法
Snowflake,雪花算法是由Twitter开源的分布式ID生成算法,以划分命名空间的方式将 64-bit位分割成多个部分,每个部分代表不同的含义。这种就是将64位划分为不同的段,每段代表不同的涵义,基本就是时间戳、机器ID和序列数。…...
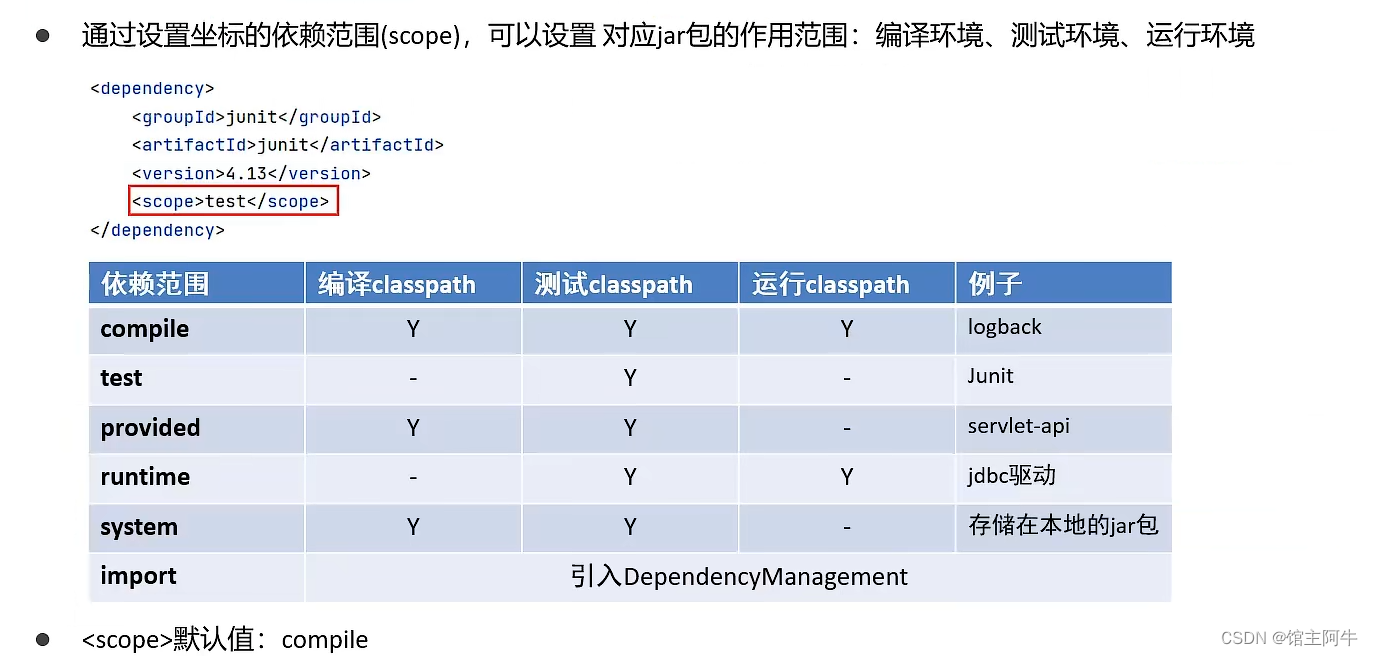
【java web篇】Maven的基本使用以及IDEA 配置Maven
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...

【蓝桥集训】第七天并查集
作者:指针不指南吗 专栏:Acwing 蓝桥集训每日一题 🐾或许会很慢,但是不可以停下来🐾 文章目录1.亲戚2.合并集合3.连通块中点的数量有关并查集的知识学习可以移步至—— 【算法】——并查集1.亲戚 或许你并不知道&#…...

【Playwright】扑面而来的Playwright测试框架
在当今快节奏的开发环境中,测试是软件开发的重要组成部分。 Microsoft Playwright 是一种流行的测试自动化框架,允许开发人员为 Web 应用程序编写端到端测试。 Playwright 建立在 Puppeteer 之上,这是另一个流行的测试自动化框架。在这篇博文…...
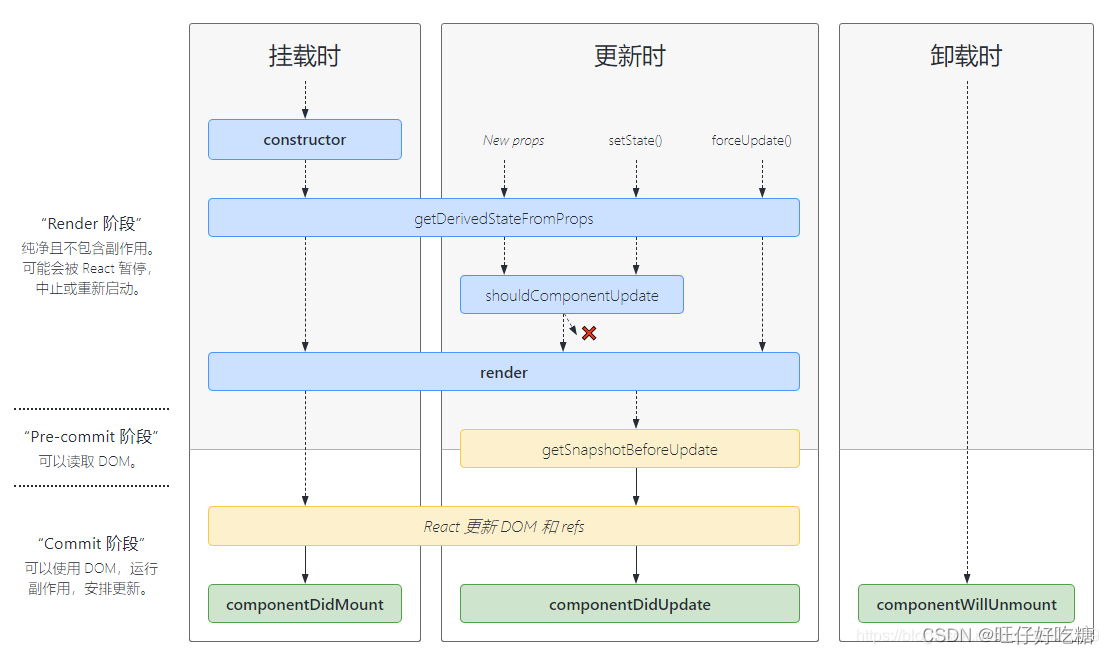
React(三) ——新、旧生命周期
🧁个人主页:个人主页 ✌支持我 :点赞👍收藏🌼关注🧡 文章目录⛳React生命周期🌋初始化阶段👣运行中阶段🏓销毁阶段🏫新生命周期的替代🚚react中性…...

IT男的一次中年破局尝试--出书
一、转战外企 接上回《人到中年——IT男择业感悟》后,自己从大央企去了某知名外企。外企虽然最近几年的日子已经没有10年前的辉煌与滋润,但相对来说,还能勉强找到工作与生活的平衡点。 划重点,35岁上下的人换工作理由…...

Python 内置函数eval()
Python 内置函数eval() eval(expression, globalsNone, localsNone) 函数用来执行一个字符串表达式,并返回表达式的值。 expression: 字符串表达式。global: 可选,globals必须是一个字典。locals: 可选,locals可以是任何映射对象。 示例 &…...

【ArcGIS Pro二次开发】系列学习笔记,持续更新,记得收藏
一、前言 这个系列是本人的一个学习笔记。 作为一个ArcGIS Pro二次开发的初学者,最困扰的就是无从入手。网上关于ArcGIS Pro二次开发的中文资料极少,官方文档对于我这样的英文苦手又太不友好。 在搜索无果后,决定自已动手,从头…...

EasyRecovery16MAC苹果版本Photo最新版数据恢复软件
无论是在工作学习中,还是在生活中,Word、Excle等办公软件都是大家很常用的。我们在使用电脑的过程中,有时会因自己的误删或电脑故障,从而导致我们所写的文档丢失了。出现这样的大家不要着急,今天小编就给大家推荐一款可…...

Go的string与strings.Builder
Go的string与strings.Builder 文章目录Go的string与strings.Builder一、strings.Builder 的优势二、string类型的值三、与string相比,Builder的优势体现在拼接方面3.1 Builder的拼接,与Builder的自动扩容3.2 手动扩容3.3 Builder 的重用四、strings.Buil…...

8.Spring Security 权限控制
1.简介入门JavaEE和SpringMVC :Spring Security就是通过11个Fliter进行组合管理小Demouser实体类user.type字段,0普通用户,1超级管理员,2版主补全get set tostringimplement UserDetails,重写以下方法// true: 账号未过…...

curl / python+selenium爬取网页信息
Python爬取网页信息 需求: 持续爬取某嵌入式设备配置网页上的状态信息 shell脚本 简单快速, 不用装插件只能爬取静态内容 用curl命令返回整个网页的内容用grep命令抓取其中某些字段结合正则表达式可多样查找但对于动态内容, 比如对某嵌入式设备配置网页上的一条不断更新的信…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
