Python 内置函数eval()
Python 内置函数eval()

eval(expression, globals=None, locals=None) 函数用来执行一个字符串表达式,并返回表达式的值。
- expression: 字符串表达式。
- global: 可选,globals必须是一个字典。
- locals: 可选,locals可以是任何映射对象。
示例
>>> x = 1
>>> eval('x + 1')
2>>> eval('pow(2, 3)')
8>>> eval('[1, 2, 3]')
[1, 2, 3]>>> eval('{"name": "白子画", "age": 1000}')
{'name': '白子画', 'age': 1000}将Json字符串转为Python字典
>>> msg = '{"name": "白子画", "married": false, "spouse": null}'
>>> eval(msg)
Traceback (most recent call last):File "<stdin>", line 1, in <module>File "<string>", line 1, in <module>
NameError: name 'false' is not defined由于Json中的布尔类型、空类型与Python中的不一致,所以直接用eval(expression)将会报错。
有两种方法可以解决:
-
方法一:转换之前先定义好无法识别的类型。
>>> false = False >>> null = None >>> msg = '{"name": "白子画", "married": false, "spouse": null}' >>> eval(msg) {'name': '白子画', 'married': False, 'spouse': None} -
方法二:转换时携带定义无法识别类型的字典。
>>> msg = '{"name": "白子画", "married": false, "spouse": null}' >>> eval(msg, {'false': False, "null": None}) {'name': '白子画', 'married': False, 'spouse': None}
相关文章:

Python 内置函数eval()
Python 内置函数eval() eval(expression, globalsNone, localsNone) 函数用来执行一个字符串表达式,并返回表达式的值。 expression: 字符串表达式。global: 可选,globals必须是一个字典。locals: 可选,locals可以是任何映射对象。 示例 &…...

【ArcGIS Pro二次开发】系列学习笔记,持续更新,记得收藏
一、前言 这个系列是本人的一个学习笔记。 作为一个ArcGIS Pro二次开发的初学者,最困扰的就是无从入手。网上关于ArcGIS Pro二次开发的中文资料极少,官方文档对于我这样的英文苦手又太不友好。 在搜索无果后,决定自已动手,从头…...

EasyRecovery16MAC苹果版本Photo最新版数据恢复软件
无论是在工作学习中,还是在生活中,Word、Excle等办公软件都是大家很常用的。我们在使用电脑的过程中,有时会因自己的误删或电脑故障,从而导致我们所写的文档丢失了。出现这样的大家不要着急,今天小编就给大家推荐一款可…...

Go的string与strings.Builder
Go的string与strings.Builder 文章目录Go的string与strings.Builder一、strings.Builder 的优势二、string类型的值三、与string相比,Builder的优势体现在拼接方面3.1 Builder的拼接,与Builder的自动扩容3.2 手动扩容3.3 Builder 的重用四、strings.Buil…...

8.Spring Security 权限控制
1.简介入门JavaEE和SpringMVC :Spring Security就是通过11个Fliter进行组合管理小Demouser实体类user.type字段,0普通用户,1超级管理员,2版主补全get set tostringimplement UserDetails,重写以下方法// true: 账号未过…...

curl / python+selenium爬取网页信息
Python爬取网页信息 需求: 持续爬取某嵌入式设备配置网页上的状态信息 shell脚本 简单快速, 不用装插件只能爬取静态内容 用curl命令返回整个网页的内容用grep命令抓取其中某些字段结合正则表达式可多样查找但对于动态内容, 比如对某嵌入式设备配置网页上的一条不断更新的信…...

晶体塑性有限元 Abaqus 三维泰森多边形(voronoi模型)插件 V7.0
1 上一版本完整功能介绍: Voronoi晶体插件-6.0版本[新功能介绍] 晶体塑性有限元 Abaqus 三维泰森多边形(voronoi模型)插件 V6.0 2 新增功能模块 7.0版本新增功能模块包括:柱状晶体模块和分层晶体模块。 2.1 二维柱状晶体模块 …...

CPython解释器性能分析与优化
原文来自微信公众号“编程语言Lab”:CPython 解释器性能分析与优化 搜索关注 “编程语言Lab”公众号(HW-PLLab)获取更多技术内容! 欢迎加入 编程语言社区 SIG-元编程 参与交流讨论(加入方式:添加文末小助手…...
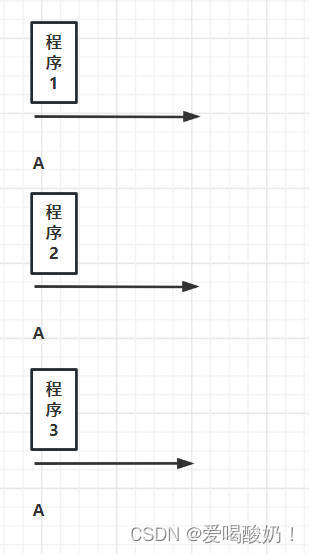
Linux 进程:理解进程和pcb
目录一、进程的概念二、CPU分时机制三、并发与并行1.并发2.并行四、pcb的概念一、进程的概念 什么是进程? 进程就是进行中的程序,即运行中的应用程序。比如:电脑上打开的LOL、QQ…… 这些都是一个个的进程。 什么是应用程序? 应用…...
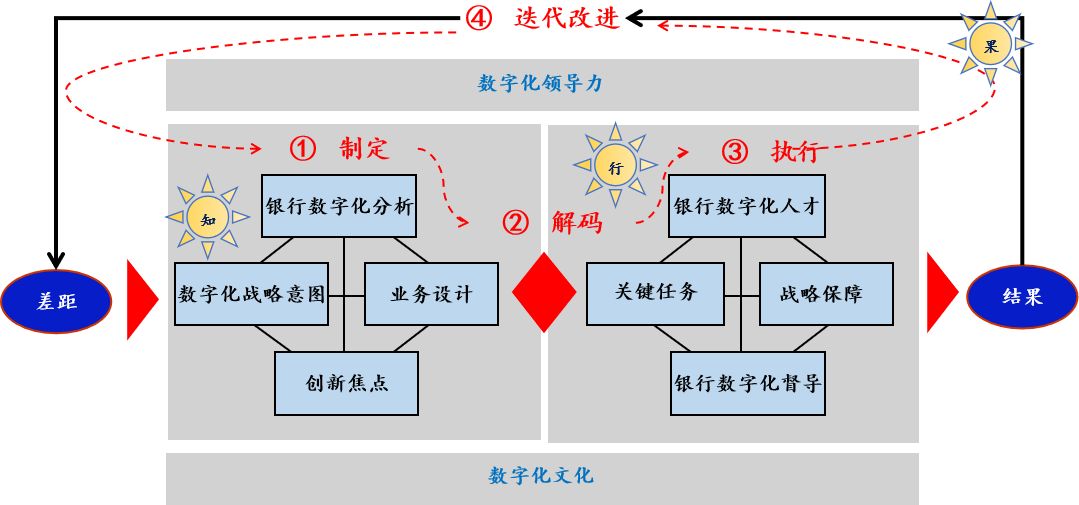
银行数字化转型导师坚鹏:招商银行数字化转型战略研究
招商银行数字化转型战略研究课程背景: 很多银行存在以下问题:不清楚如何制定银行数字化转型战略?不知道其它银行的数字化转型战略是如何演变的? 课程特色:用实战案例解读招商银行数字化转型战略。用独特视角解…...
java 一文讲透面向对象 (20万字博文)
目录 一、前言 二、面向对象程序设计介绍 1.oop三大特性 : 2.面向对象和面向过程的区别 : 3.面向对象思想特点 : 4.面向对象的程序开发 : 三、Java——类与对象 1.java中如何描述一个事物? 2.什么是类? 3.类的五大成员: 4.封装的前提——抽象 : 5.什么是对…...
使用file-selector-button美化原生文件上传
前言 你平时见到的上传文件是下面这样的? 还是下面这种美化过的button样式 还是下面这种复杂的上传组件。 <input type="file" >:只要指定的是type类型的input,打开浏览器就是上面第一种原生的浏览器默认的很丑的样式。 下面的两种是我从ElementUI截的图,…...

0402换元积分法-不定积分
文章目录1 第一类换元法1.1 定理11.2 例题1.2 常见凑微分形式1.2.1常见基本的导数公式的逆运算1.2.2被积函数含有三角函数2 第二类换元法2.1 定理22.2 常见第二换元代换方法2.2.1 三角代换-弦代换2.2.2 三角代换-切代换2.2.3 三角代换-割代换2.2.4 三角代换汇总2.2.5 倒代换2.2…...
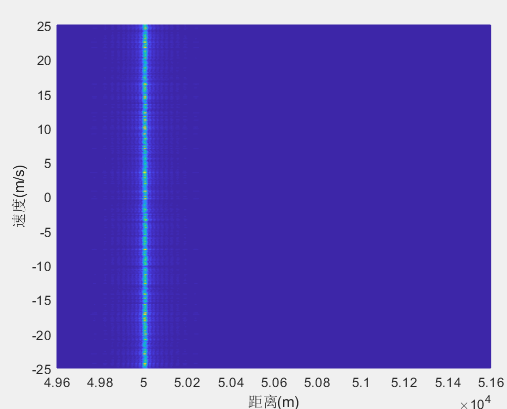
信号类型(雷达)——脉冲雷达(三)
系列文章目录 《信号类型(雷达通信)》 《信号类型(雷达)——雷达波形认识(一)》 《信号类型(雷达)——连续波雷达(二)》 文章目录 前言 一、相参雷达 1…...
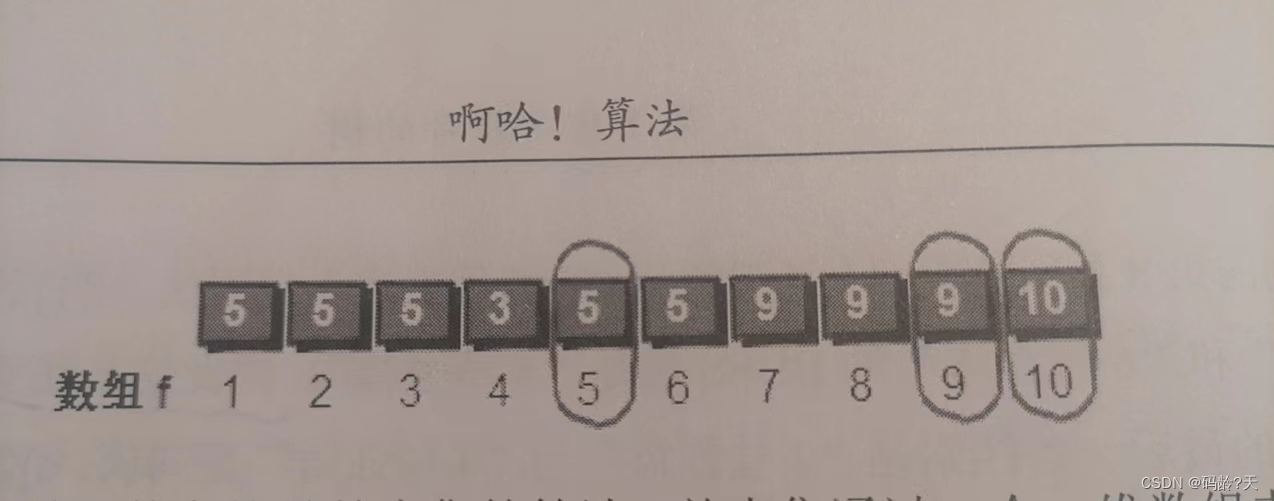
并查集(13张图解)--擒贼先擒王
目录 前言 故事 🌼思路 🌼总结 🌼代码 👊观察过程代码 👊正确代码 👊细节代码 来自《啊哈算法》 前言 刚学了树在优先队列中的应用--堆的实现 那么树还有哪些神奇的用法呢?我们从一…...
Flutter3引用原生播放器-IOS(Swift)篇
前言由于Flutter项目中需要使用到播放器功能,因此对flutter中各种播放器解决方案进行了一番研究和比对,最后决定还是自己通过Plugin的方法去引用原生播放器符合自己的需求,本篇文章会对各种解决方案做一个简单的比较,以及讲解一下…...
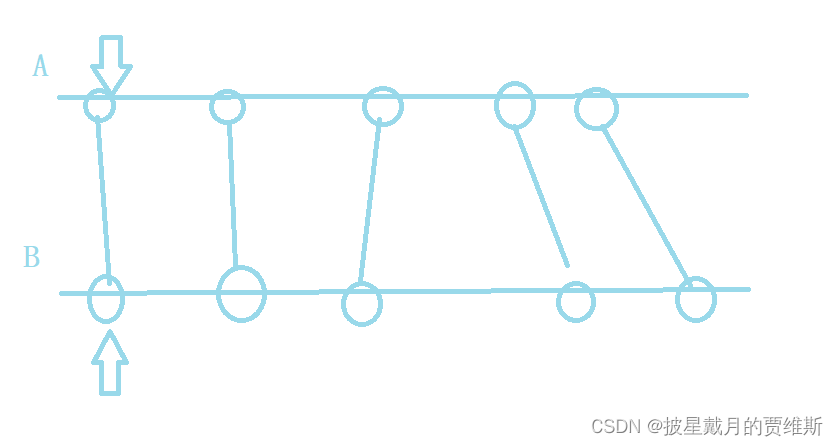
【蓝桥杯每日一题】双指针算法
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙我与杀戮之中绽放,亦如黎明的花…...
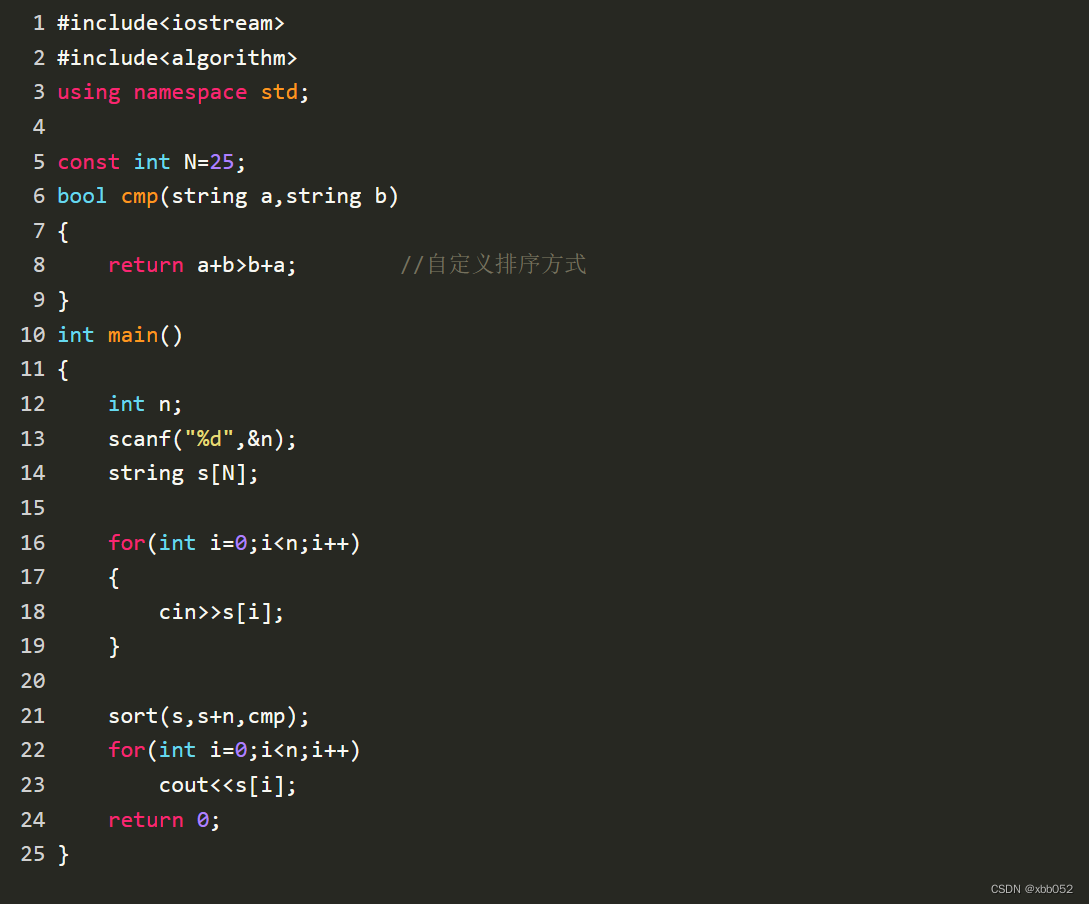
拼数(一般贪心)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题号:NC16783 时间限制:C/C 1秒,其他语言2秒 空间限制:C/C 262144K,其他语言524288K 64bit IO Format: %lld 题目描述 设有n个正整…...

LeetCode 热题 C++ 169. 多数元素 10. 正则表达式匹配 155. 最小栈
力扣169 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输出࿱…...
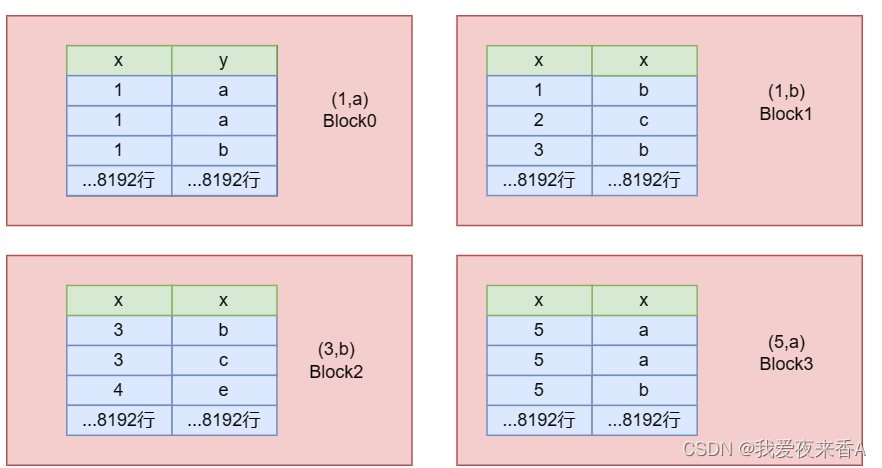
Clickhouse学习:MergeTree
MergeTree一、MergeTree逻辑存储结构二、MergeTree物理存储结构三、总结一、MergeTree逻辑存储结构 如上图所示,在排序键(CountrID、Date)上做索引,数据会按照这两个字段先后排序ClickHouse是稀疏索引,每隔8192行做一个索引,如(a,1),(a,2),比如想查a,要读取[0,3)之间的内容,稀疏…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
