晶体塑性有限元 Abaqus 三维泰森多边形(voronoi模型)插件 V7.0
1 上一版本完整功能介绍:
Voronoi晶体插件-6.0版本[新功能介绍]
晶体塑性有限元 Abaqus 三维泰森多边形(voronoi模型)插件 V6.0
2 新增功能模块
7.0版本新增功能模块包括:柱状晶体模块和分层晶体模块。
2.1 二维柱状晶体模块
该模块支持生成二维各项异性晶体模型,生成的晶体为细长形晶体。

图2.1 二维柱状晶体模块
2.2 二维分层晶体模块
该模块支持生成多层晶体模型,每一层可设置不同厚度和晶体大小,晶体的层数支持多达20层。

图2.2 二维分层晶体模块
2.3 三维柱状晶体模块
该模块支持生成二维各项异性晶体模型,支持矩形边界和圆柱体边界,可生成的晶体为细长或扁平形晶体。

图2.3 三维柱状晶体模块(矩形边界)

图2.4 三维柱状晶体模块(圆柱边界)
插件支持生成的细长和扁平形柱状三维晶体模型,示例如下:
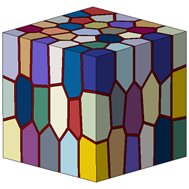
图(a) 单方向缩放三维柱状晶体模型

图(b) 双方向缩放三维柱状晶体模型
图2.5 细长和扁平形柱状三维晶体模型
2.4 三维分层晶体模块
该模块支持生成柱状晶体模型,支持矩形边界和圆柱体边界。每一层可设置不同厚度和晶体大小,晶体的层数支持多达20层。

图2.6 三维分层晶体模块(矩形边界)

图2.7 三维分层晶体模块(圆柱边界)
3 功能模块更新
7.0版本功能模块更新包括:离散晶体模块和自定义离散晶体模块,7.0版本后两个模块均支持闵式距离(包括:欧氏距离(Euclidean Distance),曼哈顿距离(Manhattan Distance),切比雪夫距离(Chebyshev Distance)及其他距离),默认为欧式距离。

图3.1 离散晶体模块(新版)

图3.2 自定义离散晶体模块(新版)
不同距离选项下的离散晶体模型生成示例:

图3.3 不同距离选项下的离散晶体模型
4 新的泡沫结构模型
插件支持柱状和分层泡沫结构模型,示例如下:

最后,如有需要欢迎通过“320科技工作室”公众号联系我们。
相关文章:

晶体塑性有限元 Abaqus 三维泰森多边形(voronoi模型)插件 V7.0
1 上一版本完整功能介绍: Voronoi晶体插件-6.0版本[新功能介绍] 晶体塑性有限元 Abaqus 三维泰森多边形(voronoi模型)插件 V6.0 2 新增功能模块 7.0版本新增功能模块包括:柱状晶体模块和分层晶体模块。 2.1 二维柱状晶体模块 …...

CPython解释器性能分析与优化
原文来自微信公众号“编程语言Lab”:CPython 解释器性能分析与优化 搜索关注 “编程语言Lab”公众号(HW-PLLab)获取更多技术内容! 欢迎加入 编程语言社区 SIG-元编程 参与交流讨论(加入方式:添加文末小助手…...
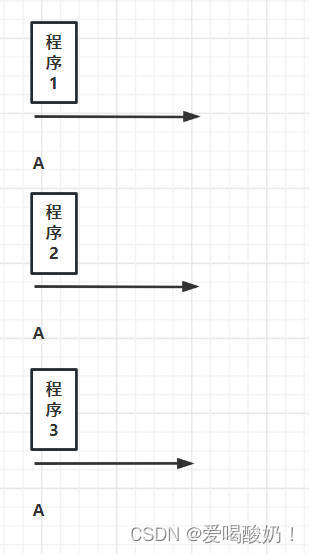
Linux 进程:理解进程和pcb
目录一、进程的概念二、CPU分时机制三、并发与并行1.并发2.并行四、pcb的概念一、进程的概念 什么是进程? 进程就是进行中的程序,即运行中的应用程序。比如:电脑上打开的LOL、QQ…… 这些都是一个个的进程。 什么是应用程序? 应用…...
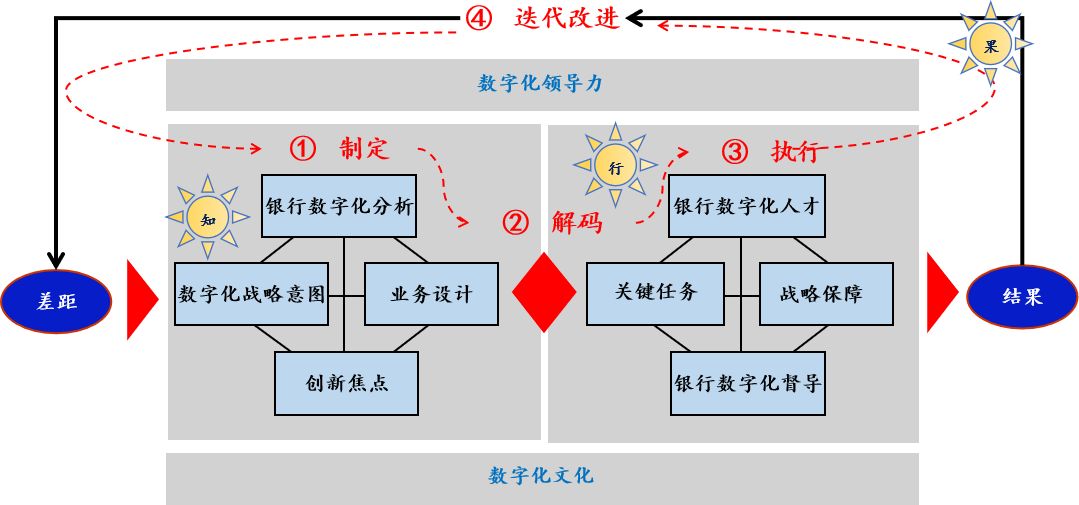
银行数字化转型导师坚鹏:招商银行数字化转型战略研究
招商银行数字化转型战略研究课程背景: 很多银行存在以下问题:不清楚如何制定银行数字化转型战略?不知道其它银行的数字化转型战略是如何演变的? 课程特色:用实战案例解读招商银行数字化转型战略。用独特视角解…...
java 一文讲透面向对象 (20万字博文)
目录 一、前言 二、面向对象程序设计介绍 1.oop三大特性 : 2.面向对象和面向过程的区别 : 3.面向对象思想特点 : 4.面向对象的程序开发 : 三、Java——类与对象 1.java中如何描述一个事物? 2.什么是类? 3.类的五大成员: 4.封装的前提——抽象 : 5.什么是对…...
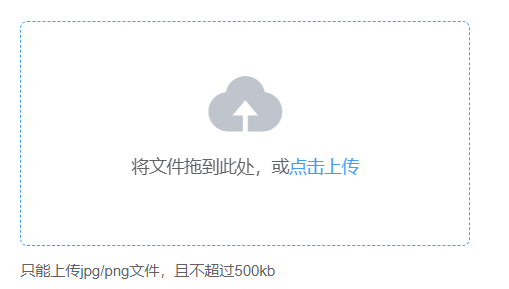
使用file-selector-button美化原生文件上传
前言 你平时见到的上传文件是下面这样的? 还是下面这种美化过的button样式 还是下面这种复杂的上传组件。 <input type="file" >:只要指定的是type类型的input,打开浏览器就是上面第一种原生的浏览器默认的很丑的样式。 下面的两种是我从ElementUI截的图,…...

0402换元积分法-不定积分
文章目录1 第一类换元法1.1 定理11.2 例题1.2 常见凑微分形式1.2.1常见基本的导数公式的逆运算1.2.2被积函数含有三角函数2 第二类换元法2.1 定理22.2 常见第二换元代换方法2.2.1 三角代换-弦代换2.2.2 三角代换-切代换2.2.3 三角代换-割代换2.2.4 三角代换汇总2.2.5 倒代换2.2…...
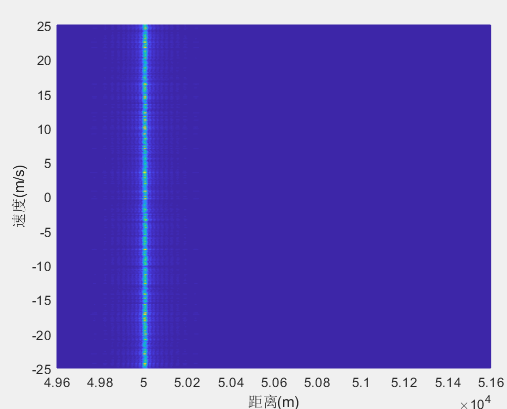
信号类型(雷达)——脉冲雷达(三)
系列文章目录 《信号类型(雷达通信)》 《信号类型(雷达)——雷达波形认识(一)》 《信号类型(雷达)——连续波雷达(二)》 文章目录 前言 一、相参雷达 1…...
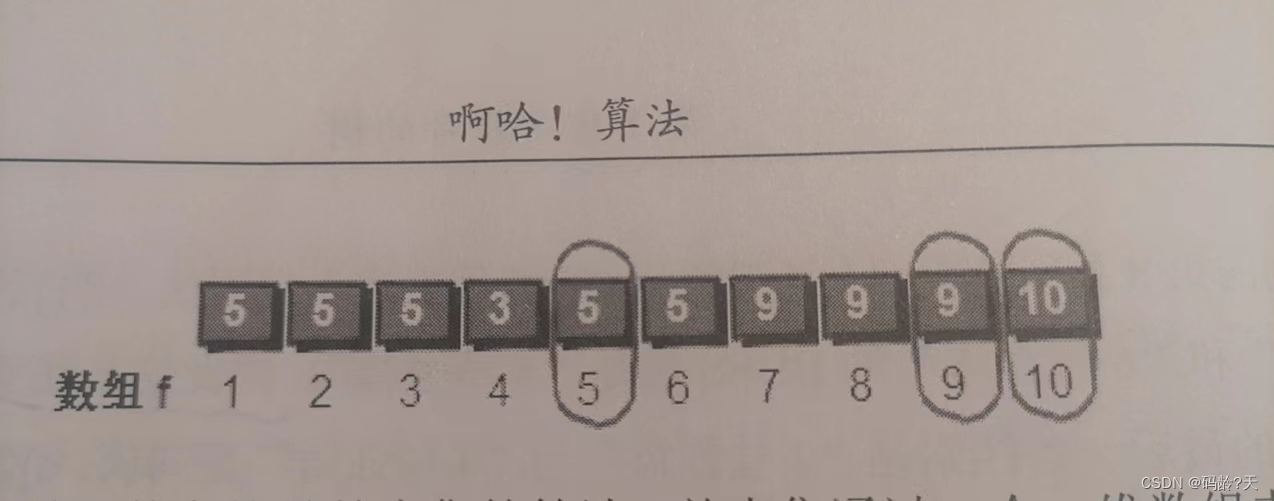
并查集(13张图解)--擒贼先擒王
目录 前言 故事 🌼思路 🌼总结 🌼代码 👊观察过程代码 👊正确代码 👊细节代码 来自《啊哈算法》 前言 刚学了树在优先队列中的应用--堆的实现 那么树还有哪些神奇的用法呢?我们从一…...
Flutter3引用原生播放器-IOS(Swift)篇
前言由于Flutter项目中需要使用到播放器功能,因此对flutter中各种播放器解决方案进行了一番研究和比对,最后决定还是自己通过Plugin的方法去引用原生播放器符合自己的需求,本篇文章会对各种解决方案做一个简单的比较,以及讲解一下…...
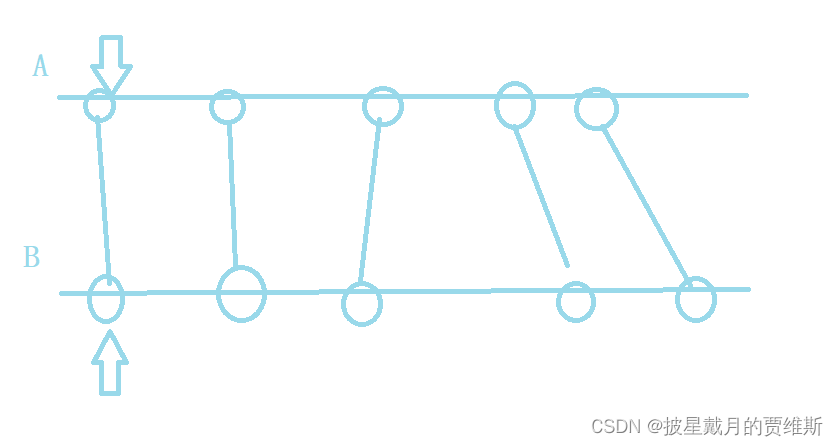
【蓝桥杯每日一题】双指针算法
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙我与杀戮之中绽放,亦如黎明的花…...
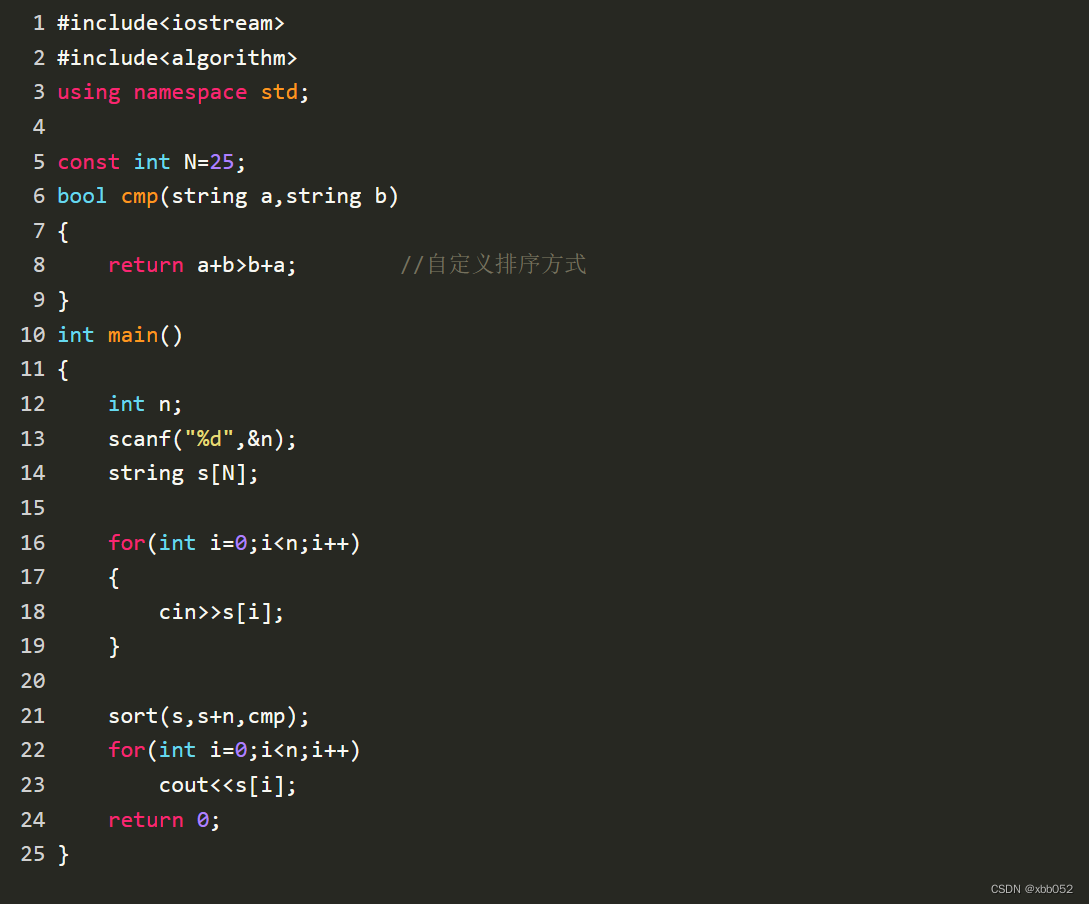
拼数(一般贪心)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题号:NC16783 时间限制:C/C 1秒,其他语言2秒 空间限制:C/C 262144K,其他语言524288K 64bit IO Format: %lld 题目描述 设有n个正整…...

LeetCode 热题 C++ 169. 多数元素 10. 正则表达式匹配 155. 最小栈
力扣169 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输出࿱…...
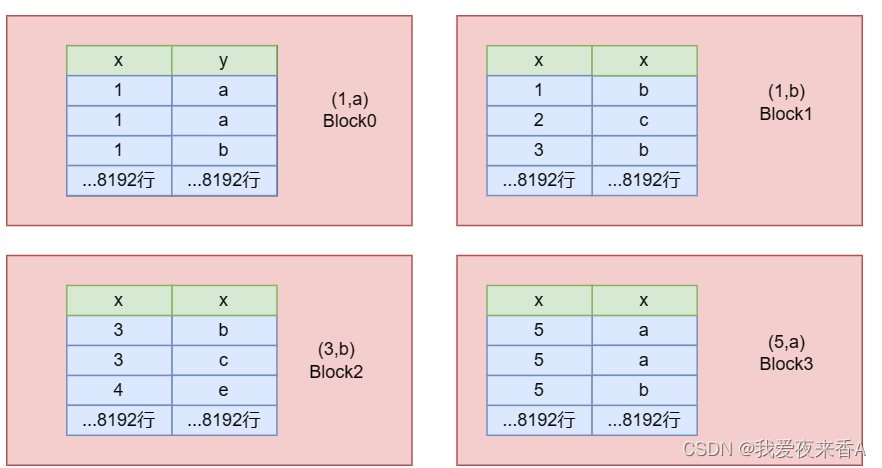
Clickhouse学习:MergeTree
MergeTree一、MergeTree逻辑存储结构二、MergeTree物理存储结构三、总结一、MergeTree逻辑存储结构 如上图所示,在排序键(CountrID、Date)上做索引,数据会按照这两个字段先后排序ClickHouse是稀疏索引,每隔8192行做一个索引,如(a,1),(a,2),比如想查a,要读取[0,3)之间的内容,稀疏…...
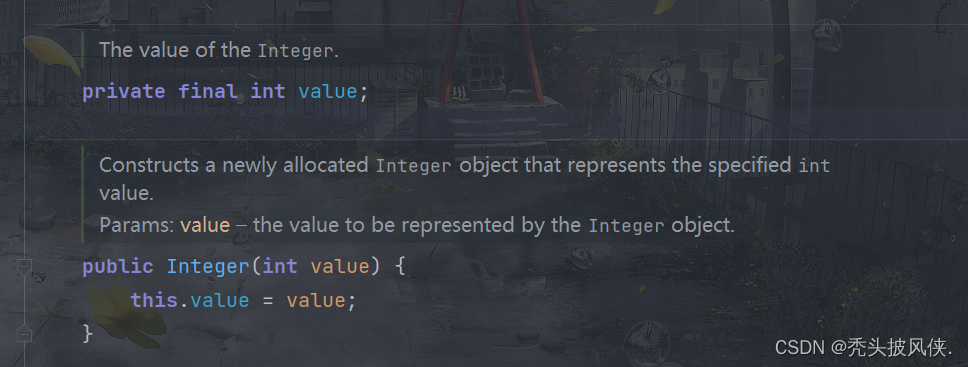
【java基础】包装类,自动装箱和自动拆箱
文章目录基本介绍包装类自动装箱自动拆箱包装类注意事项包装类比较包装器内容不可变基本介绍 有时,需要将int这样的基本类型转换为对象。所有的基本类型都有一个与之对应的类。 例如,Integer类对应基本类型int。通常,这些类称为包装器&#…...
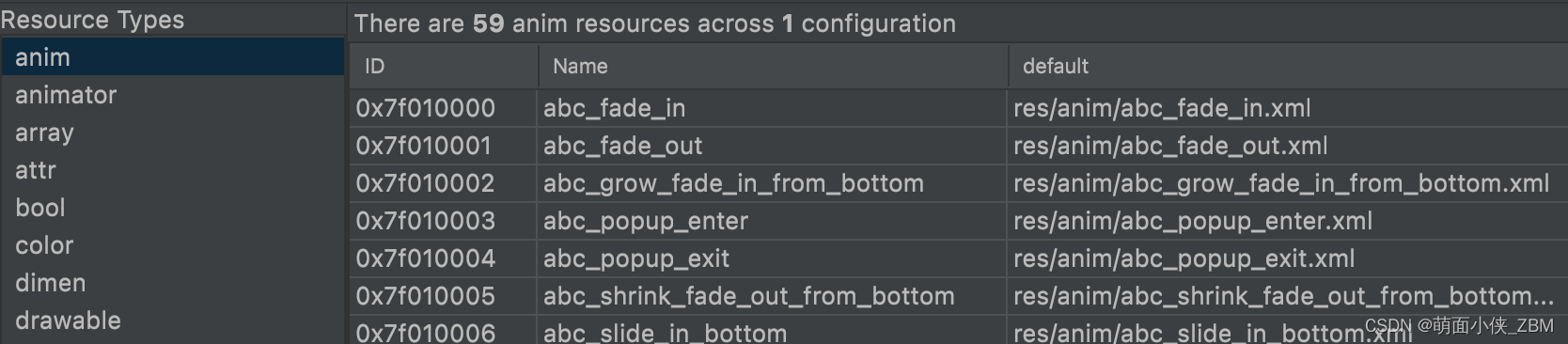
Android笔记(二十五):两种sdk热更插件资源加载方案
背景 在研究sdk插件化热更新方式的过程中总结出了两套插件资源加载方案,在此记录下 资源热更方式 方式一:合并所有插件资源 需要解决资源id冲突问题 资源ID值一共4个字段,由三部分组成:PackageIdTypeIdEntryId PackageId&…...

spring框架--全面详解(学习笔记)
目录 1.Spring是什么 2.Spring 框架特点 3.Spring体系结构 4.Spring开发环境搭建 5.spring中IOC和DI 6.Spring中bean的生命周期 7.Spring Bean作用域 8.spring注解开发 9.Spring框架中AOP(Aspect Oriented Programming) 10.AOP 实现分类 11.A…...
)
2023年CDGA考试模拟题库(401-500)
2023年CDGA考试模拟题库(401-500) 401.数据管理战略的SMART原则指的是哪项? [1分] A.具体 、高质量、可操作 、现实、有时间限制 B.具体、可衡量、可检验、现实、有时间限制 C.具体、可衡量、可操作、现实、有时间限制 D.具体、高质量、可检验、现实12-24个月的目标 答…...

软件设计师备考文档
cpu 计算机的基本硬件系统:运算器、控制器、存储器、输入设备、输出设备 cpu负责获取程序指令,对指令进行译码并加以执行 * cpu的功能控制器(保证程序正常执行,处理异常事件) 程序控制操作控制运算器(只能…...
)
Javascript的API基本内容(一)
一、获取DOM对象 querySelector 满足条件的第一个元素 querySelectorAll 满足条件的元素集合 返回伪数组 document.getElementById 专门获取元素类型节点,根据标签的 id 属性查找 二、操作元素内容 通过修改 DOM 的文本内容,动态改变网页的内容。 inn…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
