分治法求解棋盘覆盖问题
分治法求解棋盘覆盖问题
如何应用分治法求解棋盘覆盖问题呢?分治的技巧在于如何划分棋盘,使划分后的子棋盘的大小相同,并且每个子棋盘均包含一个特殊方格,从而将原问题分解为规模较小的棋盘覆盖问题。
基本思路
棋盘覆盖问题是指在一个大小为2n * 2n的棋盘上,去掉其中一个方格后,用L型骨牌(覆盖3个方格)将其完全覆盖。分治法是一种解决该问题的有效算法。
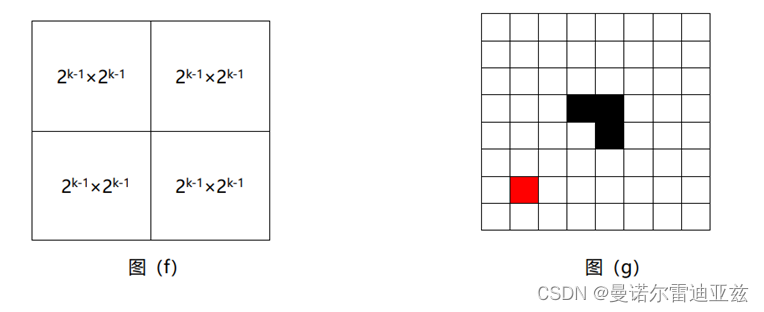
当 k>0 时,将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k - 1)子棋盘,如下图(f)所示。特殊方格必位于4 个较小子棋盘之一种,其余 3 个子棋盘中无特殊方格。为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘,可以用一个 L 型骨牌覆盖这 3 个较小棋盘的会合处,如下图(g)所示。从而将原问题转化为 4 个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为棋盘 1*1。
代码实现
#include <stdio.h>
int board[100][100] = { 0 };
int tile = 1;
//棋盘覆盖
void ChessBoard(int tr, int tc, int dr, int dc, int size) {if (size == 1)return;int t = ++tile,s = size / 2;//覆盖左上角棋盘if (dr < tr + s && dc < tc + s)//特殊方格在棋盘中{ChessBoard(tr, tc, dr, dc, s);}else {//特殊方格不在棋盘中,则从中间覆盖一个方格board[tr + s - 1][tc + s - 1] = t; //赋值特殊方格类型ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);//从左上角继续划分 }//覆盖右上角棋盘if (dr < tr + s && dc >= tc + s)//特殊方格在棋盘中{ChessBoard(tr, tc + s, dr, dc, s);}else {//特殊方格不在棋盘中,则从中间覆盖一个方格board[tr + s - 1][tc + s] = t; //赋值特殊方格类型ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);//从右上角继续划分 }//覆盖左下角棋盘if (dr >= tr + s && dc < tc + s)//特殊方格在棋盘中{ChessBoard(tr + s, tc, dr, dc, s);}else {//特殊方格不在棋盘中,则从中间覆盖一个方格board[tr + s][tc + s - 1] = t; //赋值特殊方格类型ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);//从左下角继续划分 }//覆盖右下角棋盘if (dr >= tr + s && dc >= tc + s)//特殊方格在棋盘中{ChessBoard(tr + s, tc + s, dr, dc, s);}else {//特殊方格不在棋盘中,则从中间覆盖一个方格board[tr + s][tc + s] = t; //赋值特殊方格类型ChessBoard(tr + s, tc + s, tr + s, tc + s, s);//从左下角继续划分 }
}
int main(void) {int size, dr, dc;printf("请输入棋盘的行或列号:");scanf("%d", &size);printf("请输入特殊方格的行或列号:");scanf("%d %d", &dr, &dc);board[dr][dc] = 1;ChessBoard(0, 0, dr, dc, size);for (int i = 0;i < size;i++) {for (int j = 0;j < size;j++)printf("%d\t", board[i][j]);printf("\n");}return 0;
}
运行结果
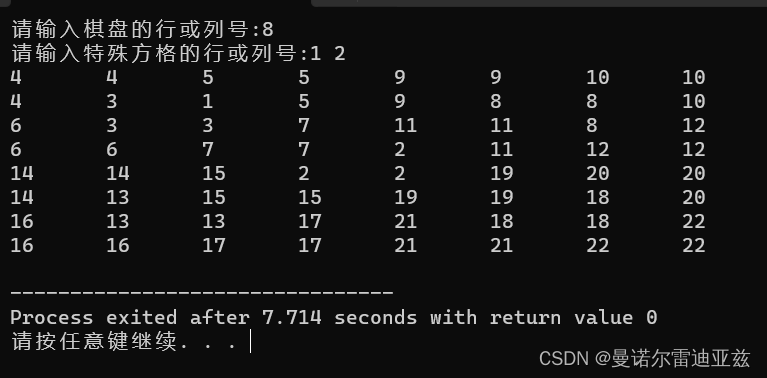
如上图所示,相同的数字就代表了一个L型的骨牌。
相关文章:

分治法求解棋盘覆盖问题
分治法求解棋盘覆盖问题 如何应用分治法求解棋盘覆盖问题呢?分治的技巧在于如何划分棋盘,使划分后的子棋盘的大小相同,并且每个子棋盘均包含一个特殊方格,从而将原问题分解为规模较小的棋盘覆盖问题。 基本思路 棋盘覆盖问题是…...

爱写bug的小邓程序员个人博客
博客网址: http://www.006969.xyz 欢迎来到我的个人博客,这里主要分享我对于前后端相关技术的学习笔记、项目实战经验以及一些技术感悟。 在我的博客中,你将看到以下主要内容: 技术文章 我将会分享我在学习前后端技术过程中的一些感悟&am…...

selenium判断元素可点击、可见、可选
1、判断元素是否可以点击 判断元素是否可以点击,WebElement对象调用is_enabled() is_enabled()方法返回一个布尔值,若可点击返回:True。若不可点击则返回:False from selenium import webdriver import time from selenium.web…...

计算机网络重点概念整理-第六章 应用层【期末复习|考研复习】
计算机网络复习系列文章传送门: 第一章 计算机网络概述 第二章 物理层 第三章 数据链路层 第四章 网络层 第五章 传输层 第六章 应用层 第七章 网络安全 计算机网络整理-简称&缩写 文章目录 前言六、应用层6.1 网络应用模型6.1.1 客户/服务器模式C/S模型6.1.2 P…...

html2pdf
页面布局时将需要保存在同一页pdf的dom元素用div包裹,并为该div添加class类名,例如.convertPDF,如果有多页创建多个.convertPDF这个div,再循环保存pdf即可 用到了html2canvas和JsPdf这两个插件,自行站内搜索安装 pdf页…...

css中页面元素隐藏
display:nonevisibility:hiddenopcity:0页面中不存在存在存在重排会不会不会重绘会会不一定自身绑定事件不触发不触发能触发transition不支持支持支持子元素可复原不能能不能被遮挡的元素可触发事件能能不能 其他: 1.设置height,width,margi…...

dp三步问题
三步问题 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 class Solution { public:int waysToStep(int n) {vector<int> dp(n1,1);if(n1) return 1;dp[1]1;dp[2]2;for(int i3; i<n1; i){dp[i] ((dp[i-1]dp[i-2])%1000000007dp[i-3])%100…...

结构体和联合体嵌套访问
在JSON项目中,使用了联合体和结构体之间的嵌套,但是在访问内部的联合体和结构体的时候出现了问题,这篇文章作为记录,也希望能帮助遇到相同问题的好伙伴。 struct lept_value {union {struct str{char *s;size_t len;};double n;}…...

Linux ———— 管理磁盘
(一)MBR硬盘与GPT硬盘 硬盘按分区表的格式可以分为MBR硬盘与GPT硬盘两种硬盘格式。 MBR 硬盘:使用的是旧的传统硬盘分区表格式,其硬盘分区表存储在MBR(Master Boot Record,主引导区记录)内。MBR位于…...

文字的编码
1 字符的编码方式 1.1 ASCII 是“American Standard Code for Information Interchange”的缩写,美国信息交换标准代码。电脑毕竟是西方人发明的,他们常用字母就 26 个,区分大小写、加上标点符号也没超过 127 个,每个字符用一个字…...
21.9 Python 使用Selenium库
Selenium是一个自动化测试框架,主要用于Web应用程序的自动化测试。它可以模拟用户在浏览器中的操作,如打开网页、点击链接、填写表单等,并且可以在代码中实现条件判断、异常处理等功能。Selenium最初是用于测试Web应用程序的,但也…...
C++初阶2
目录 一,auto关键字 1-1,auto的使用 1-2,基于范围auto的for循环 二,nullptr的运用 三,C类的初步学习 3-1,类的引用 3-2,类的访问权限 3-3,类的使用 1,类中函数的…...

网络安全(黑客)—小白自学
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...

在win10下,使用torchviz对深度学习网络模型进行可视化
目录 1. 安装 graphviz 和 torchviz 2.安装 graphviz.exe 3.实例测试 4.如果你的电脑还是无法画图,并且出现了下面的报错: 5.参考文章: 1. 安装 graphviz 和 torchviz 首先打开 Anaconda prompt 进入自己的 pytorch 环境(图中 pt 是我自…...

【自然语言处理】【长文本处理】RMT:能处理长度超过一百万token的Transformer
相关博客 【自然语言处理】【长文本处理】RMT:能处理长度超过一百万token的Transformer 【自然语言处理】【大模型】MPT模型结构源码解析(单机版) 【自然语言处理】【大模型】ChatGLM-6B模型结构代码解析(单机版) 【自然语言处理】【大模型】BLOOM模型结构源码解析(…...
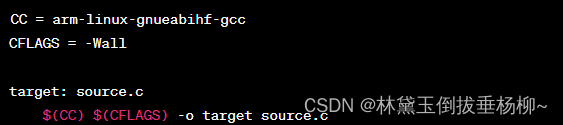
交叉编译工具链(以STM32MP1为例)
1.什么是交叉编译工具链? 在一个系统上进行编译,在另一个系统上进行执行 2.STM32MP1交叉编译工具链 3.交叉编译器内容 4.两种工具链模式 5.两种链接模式 6.工具使用 注意:OpenSTLinux已经提供了编译框架,不需要命令行手工编译 …...
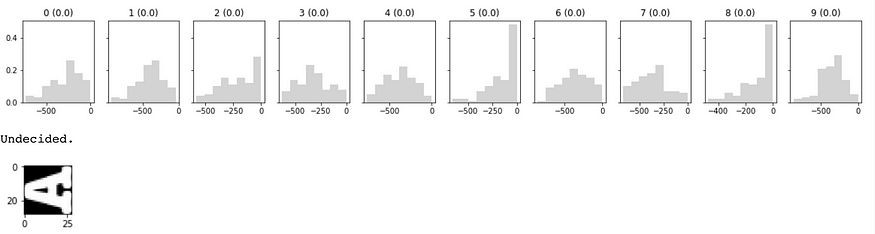
使用 Pyro 和 PyTorch 的贝叶斯神经网络
一、说明 构建图像分类器已成为新的“hello world”。还记得当你第一次接触 Python 时,你的打印“hello world”感觉很神奇吗?几个月前,当我按照PyTorch 官方教程并为自己构建了一个运行良好的简单分类器时,我也有同样的感觉。 我…...

How to install the console system of i-search rpa on Centos 7
How to install the console system of i-search rpa on Centos 7 1、 准备1.1 、查看磁盘分区状态1.2、上传文件1.2.1、添加上传目录1.2.2、上传安装包1.2.3、解压安装包1.2.4、查看安装包结构 1.3、安装依赖包1.3.1、基础依赖包1.3.2 相关依赖 1.4、关闭防火墙1.5、解除SeLin…...
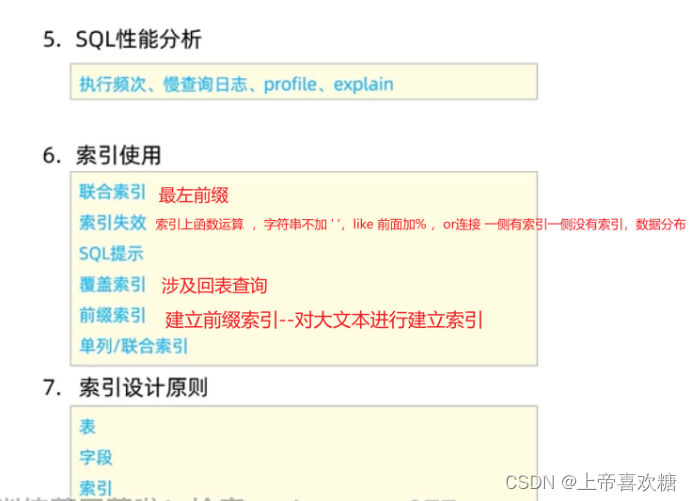
sql--索引使用 ---覆盖索引
覆盖索引 Select 后接 * 走id索引才是最优,使用二级索引则需要回表(性能稍差) 前缀索引 Create index 索引名 on 表名( 字段名( n ) ) n数字 n代表提取这个字符串的n个构建索引 ??那么 n 为几性能是最好的呢&…...

系统平台同一网络下不同设备及进程的话题通讯--DDS数据分发服务中间件
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言(1)中间件的介绍(2)DDS介绍(3)发布者(4)订阅者(5)idl文件(定义msg结构体)(6)QoS(Quality of Service)策略(7)DDS测试工具介绍(…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
