【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别)
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问题,而这些问题是比较隐晦而且难以发现的,并且鲜有老师强调。因此,就这方面希望能够帮助同样对概率论的这部分内容有疑惑的同学。
随机变量
首先,在学习概率最开始的时候,我们接触了随机变量X,它是一种量,就是说它是变化的(这是我的理解方式)。对于这个随机变量X,我们怎么样才能让它定下来呢?通过抽样的方式。
举个例子,随机变量X(我其实感觉这个地方和最开始的事件容易混淆,我姑且把事件和随机变量混为一谈了(这个部分博友有更好的说法恳请指正))我可以说是抛硬币了,那么我只有抛了,才能知道这个值是多少,否则单论这个量(抛硬币),我是不能得出任何有用的信息的,我们只有通过抛硬币,才能发现X,X是抽象的,是被我们观察了无数次的实验结果所定义的(我姑且这么阐释了)。
当硬币抛出后,我们有了第一个样本x1,这个不一样了,我们叫它样本值x1,它是一个值。是有确切的大小的。至此,我们的前三章的值和量解决完毕。
数字特征
在第四章,我们接触到了新的东西,叫做数字特征,比如期望EX,方差DX,它们是确切的值,我想也是显而易见的。
对于一个随机变量X,假设它是服从标准正态分布的,显然它的期望是0,方差是1,是确定的值。
至此,我们的第四章的值和量解决完毕。
参数估计
在后面的几章中,我们接触了比较多的值和量,极大似然估计量,无偏估计量,样本均值,等等。在这里我们抽取两组进行说明,(样本均值,样本方差)和(期望,方差),极大似然估计值和极大似然估计量。
样本均值和样本方差,他们是量(这个地方是很容易混淆的)。
期望和方差,他们是值。
可以这么理解,样本均值是X拔,是n分之1乘以X的求和,既然X是量,那么X拔当然也是量(见补充),同理可得样本方差。
对于极大似然估计值和极大似然估计量,有了前面的铺垫,我们可以比较清晰的解决了。
极大似然估计值是θ,是值。
极大似然估计量是θ尖,是量。
在求解极大似然估计的时候,我们发现,最开始求解极大似然估计值的时候,我们都是用的x。因为值要和值对应,(极大似然估计值和样本值相对应)。
在求解极大似然估计量的时候,我们发现,在最后一步往往是,我们转换成了θ尖,这个时候,对应的x变成了X,这是因为,量要和量对应(随机变量和极大似然估计量对应)。
这个应该怎么理解呢?这里给出一个我个人的看法。
虽然样本均值和样本方差都是值,但是就像在随机变量中,我们可以通过抽样x来观察X的性质一样,在样本均值和样本方差的观察中,我们也是通过抽样样本来估计样本均值和方差。
于是,在极大似然估计的时候,我们往往可以看到,前一步θ对应x,后一步就跳到θ尖对应X了,或者可以说,我们无法得到量,即便是样本的量我们也无法得到,但是我们可以用样本值去估计样本的量,因此,通过同步替换,可以达到用样本值代替(估计)量的效果。有了这个样本的估计量,我们再用样本的估计量去估计随机变量的数字特征(值)
样本的观测值 --------> 样本的估计量 --------> 随机变量的数字特征
第一步中,我们用样本的观测值代替样本的估计量,是因为我们假设我们经过足够多的观测后,我们可以得到随机变量的性质(基于大数定律),然而在现实生活中,我们不可能进行无穷无尽的观测,因此,就用有限次观测值来近似量。
在第二步中,我们用样本的估计量来计算随机变量的数字特征就是我们在第一步的假设的延拓(比如套个D或者E,本质上就是等价变形?基于第一步的假设?)(这部分差不多可能是车轱辘话了?我暂且做个不清晰的叙述了,欢迎博友进行补充)
再举一个例子,通过样本方差S方去估计随机变量的方差,我们也是通过在S方上套一个D,就可以将其变为值,就可以进行估计了(上述的第二步)
至此,我们概率论所有重要的值和量解析完毕。
补充
X是随机变量g(X)当然也是随机变量,x是样本值,g(x)当然也是值(似乎没这么考过。。)。
相关文章:
【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别))
【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别)
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问…...

NOIP2023模拟6联测27 点餐
题目大意 有 n n n样菜品,每样菜品都有两个权值 a i a_i ai和 b i b_i bi,如果你选择了 k k k个菜品,分别为 p 1 , … , p k p_1,\dots,p_k p1,…,pk,则你的花费为 ∑ i 1 k a p i max i 1 k b p i \sum\limits_{i…...
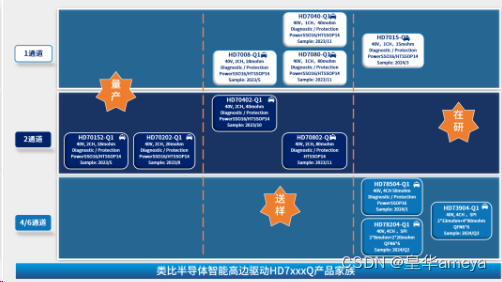
AMEYA360:类比半导体重磅发布车规级智能高边驱动HD7xxxQ系列
致力于提供高品质芯片的国内优秀模拟及数模混合芯片设计商上海类比半导体技术有限公司(下称“类比半导体”或“类比”)宣布推出重磅新品车规级智能高边驱动HD7xxxQ系列。该系列产品包括车规级单通道高边驱动HD70xxQ和车规级双通道智能高边驱动HD70xx2Q,提供不同通道…...

【HarmonyOS】鸿蒙操作系统架构
HarmonyOS架构 一. 鸿蒙系统定位二. 架构整体遵从分层设计三. HarmonyOS具有的技术特性四. HarmonyOS有三大特征 其它相关推荐: 软考系统架构之案例篇(架构设计相关概念) 系统架构之微服务架构 系统架构设计之微内核架构 所属专栏:系统架构设计师 一. 鸿…...
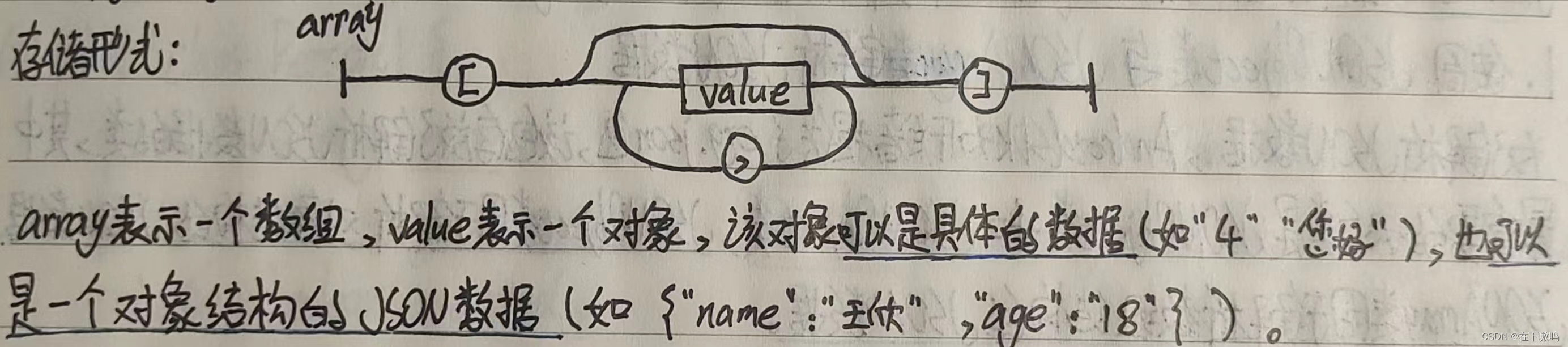
JSON数据
一、JSON介绍 Android应用程序界面上的数据信息大部分都是通过网络请求从服务器上获取到的,获取到的数据类型常见的就是JSON。JSON是一种新的数据格式,这种格式的数据不可以直接显示到程序的界面上,需要将该数据解析为一个集合或对象的形式才…...

金融领域:怎么保持电力系统连续供应?
银行作为金融领域的关键机构,依赖于高度可靠的电力供应,以保持银行操作的连续性。在电力中断或电力质量问题的情况下,银行可能面临严重的风险,包括数据丢失、交易中断和客户满意度下降。 UPS监控系统在这一背景下变得至关重要&…...
批量重命名文件夹:用数字随机重命名法管理您的文件夹
在文件管理中,文件夹的命名是一项至关重要的任务。一个好的文件夹命名方案可以帮助我们更高效地组织和查找文件。然而,随着时间的推移,我们可能会遇到文件夹数量过多,难以管理和查找的问题。为了解决这个问题,我们可以…...

RPC与HTTP的关系
首选理清楚关系 RPC与HTTP是两个不同维度的东西 HTTP 协议(Hyper Text Transfer Protocol),又叫做超文本传输协议,是一种传输协议,平时通过浏览器浏览网页网页,用到的就是 HTTP 协议。 而 RPC࿰…...

OpenCV #以图搜图:感知哈希算法(Perceptual hash algorithm)的原理与实验
1. 介绍 感知哈希算法(Perceptual Hash Algorithm,简称pHash) 是哈希算法的一种,主要用来做相似图片的搜索工作。 2. 原理 感知哈希算法(pHash)首先将原图像缩小成一个固定大小的像素图像,然后…...
Android多张图片rotation旋转角度叠加/重叠堆放
Android多张图片rotation旋转角度叠加/重叠堆放 <?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-auto"…...
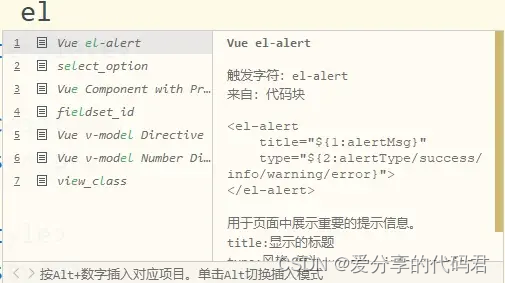
HBuilderX 自定义语法提示
在开发实践中,会使用到各种第三方组件,比如Element UI,通常的做法是到官网中复制模板再在本地根据设计要求进行修改,或是从其它已经实现的组件中复制相似的内容。但每次复制粘贴确实比较麻烦。 在HBuilderx中可以设置代码块来创建…...

Leetcode—2562.找出数组的串联值【简单】
2023每日刷题(十四) Leetcode—2562.找出数组的串联值 实现代码 long long findTheArrayConcVal(int* nums, int numsSize){int left 0;int right numsSize - 1;long long sum 0;while(left < right) {if(left right) {sum nums[left];break;}…...

T0外部计数输入
/*----------------------------------------------- 内容:通过外部按键计数进入中断执行LED取反 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存器的…...
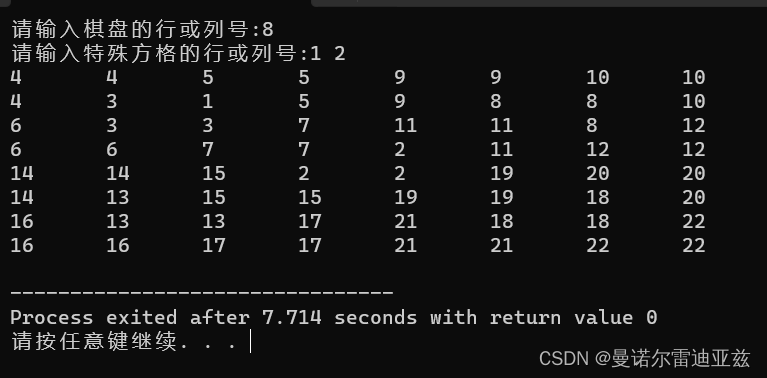
分治法求解棋盘覆盖问题
分治法求解棋盘覆盖问题 如何应用分治法求解棋盘覆盖问题呢?分治的技巧在于如何划分棋盘,使划分后的子棋盘的大小相同,并且每个子棋盘均包含一个特殊方格,从而将原问题分解为规模较小的棋盘覆盖问题。 基本思路 棋盘覆盖问题是…...

爱写bug的小邓程序员个人博客
博客网址: http://www.006969.xyz 欢迎来到我的个人博客,这里主要分享我对于前后端相关技术的学习笔记、项目实战经验以及一些技术感悟。 在我的博客中,你将看到以下主要内容: 技术文章 我将会分享我在学习前后端技术过程中的一些感悟&am…...

selenium判断元素可点击、可见、可选
1、判断元素是否可以点击 判断元素是否可以点击,WebElement对象调用is_enabled() is_enabled()方法返回一个布尔值,若可点击返回:True。若不可点击则返回:False from selenium import webdriver import time from selenium.web…...

计算机网络重点概念整理-第六章 应用层【期末复习|考研复习】
计算机网络复习系列文章传送门: 第一章 计算机网络概述 第二章 物理层 第三章 数据链路层 第四章 网络层 第五章 传输层 第六章 应用层 第七章 网络安全 计算机网络整理-简称&缩写 文章目录 前言六、应用层6.1 网络应用模型6.1.1 客户/服务器模式C/S模型6.1.2 P…...

html2pdf
页面布局时将需要保存在同一页pdf的dom元素用div包裹,并为该div添加class类名,例如.convertPDF,如果有多页创建多个.convertPDF这个div,再循环保存pdf即可 用到了html2canvas和JsPdf这两个插件,自行站内搜索安装 pdf页…...

css中页面元素隐藏
display:nonevisibility:hiddenopcity:0页面中不存在存在存在重排会不会不会重绘会会不一定自身绑定事件不触发不触发能触发transition不支持支持支持子元素可复原不能能不能被遮挡的元素可触发事件能能不能 其他: 1.设置height,width,margi…...

dp三步问题
三步问题 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 class Solution { public:int waysToStep(int n) {vector<int> dp(n1,1);if(n1) return 1;dp[1]1;dp[2]2;for(int i3; i<n1; i){dp[i] ((dp[i-1]dp[i-2])%1000000007dp[i-3])%100…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
