动态规划14:一和零
动态规划14:一和零

题目
474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 6001 <= strs[i].length <= 100strs[i]仅由'0'和'1'组成1 <= m, n <= 100
解题思路-五部曲
首先我们先把题型给确定了,这不是多重背包,实质还是01背包
多重背包是每个物品,数量不同的情况。
本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
理解成多重背包的同学主要是把m和n混淆为物品了,感觉这是不同数量的物品,所以以为是多重背包。
但本题其实是01背包问题!
只不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
-
确定dp数组含义:dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
-
确定递推公式:dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
-
dp数组初始化:因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
-
确定遍历顺序:先物后包,包要倒序,两种维度的顺序不用在意
-
debug:打印dp数组
代码示例
class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m + 1][n + 1];dp[0][0] = 0;//通过给的答案,是不考虑空集的for(String str : strs) {char[] cArr = str.toCharArray();int m0 = 0;//本字符串的0的数量int n1 = 0;//本字符串的1的数量for(char c : cArr) {if(c == '0') m0++;else n1++;}for(int i = m; i >= m0; i--) {for(int j = n; j >= n1; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - m0][j - n1] + 1);}}}return dp[m][n];}
}
- 时间复杂度: O(kmn),k 为strs的长度
- 空间复杂度: O(mn)
总结
不少同学刷过这道题,可能没有总结这究竟是什么背包。
此时我们讲解了0-1背包的多种应用,
- 纯 0 - 1 背包是求 给定背包容量 装满背包 的最大价值是多少。
- 416. 分割等和子集 是求 给定背包容量,能不能装满这个背包。
- 1049. 最后一块石头的重量 II 是求 给定背包容量,尽可能装,最多能装多少
- 494. 目标和是求 给定背包容量,装满背包有多少种方法。
- 本题是求 给定背包容量,装满背包最多有多少个物品。
这些都是 0-1背包不同维度上的应用,大家可以细心体会!
相关文章:

动态规划14:一和零
动态规划14:一和零 题目 474. 一和零 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。 …...
C#WPF嵌入字体实例
本文介绍C#WPF嵌入字体实例。 首先创建项目 添加Resources文件夹,添加字体文件,字体文件属性:生成操作为Resources,复制到输出目录:不复制 字体的使用可以采用以下两种方法: 方式一 直接引用 FontFamily="./Resources/#幼圆" 方式二 定义资源 <Applica…...

Linux——Linux权限
Linux权限 前言一、shell命令以及运行原理二、Linux权限的概念Linux权限管理文件访问者的分类(人)文件类型和访问权限(事物属性)文件权限值的表示方法文件访问权限的相关设置方法 file指令目录的权限粘滞位 总结 前言 linux的学习…...

android中gradle的kotlin编译配置选项
一、编译配置 1、Android中的配置 使用如下方式开启在Android中的gradle的kotlin编译配置: 该配置在其余平台不可用 android {...compileOptions {sourceCompatibility JavaVersion.VERSION_17targetCompatibility JavaVersion.VERSION_17}kotlinOptions {jvmTar…...
【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别))
【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别)
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问…...

NOIP2023模拟6联测27 点餐
题目大意 有 n n n样菜品,每样菜品都有两个权值 a i a_i ai和 b i b_i bi,如果你选择了 k k k个菜品,分别为 p 1 , … , p k p_1,\dots,p_k p1,…,pk,则你的花费为 ∑ i 1 k a p i max i 1 k b p i \sum\limits_{i…...
AMEYA360:类比半导体重磅发布车规级智能高边驱动HD7xxxQ系列
致力于提供高品质芯片的国内优秀模拟及数模混合芯片设计商上海类比半导体技术有限公司(下称“类比半导体”或“类比”)宣布推出重磅新品车规级智能高边驱动HD7xxxQ系列。该系列产品包括车规级单通道高边驱动HD70xxQ和车规级双通道智能高边驱动HD70xx2Q,提供不同通道…...

【HarmonyOS】鸿蒙操作系统架构
HarmonyOS架构 一. 鸿蒙系统定位二. 架构整体遵从分层设计三. HarmonyOS具有的技术特性四. HarmonyOS有三大特征 其它相关推荐: 软考系统架构之案例篇(架构设计相关概念) 系统架构之微服务架构 系统架构设计之微内核架构 所属专栏:系统架构设计师 一. 鸿…...
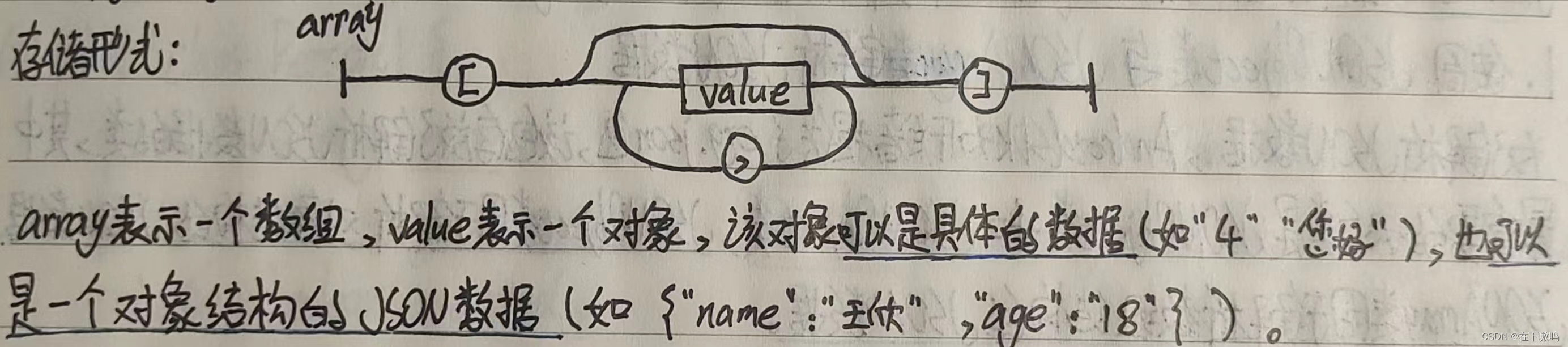
JSON数据
一、JSON介绍 Android应用程序界面上的数据信息大部分都是通过网络请求从服务器上获取到的,获取到的数据类型常见的就是JSON。JSON是一种新的数据格式,这种格式的数据不可以直接显示到程序的界面上,需要将该数据解析为一个集合或对象的形式才…...

金融领域:怎么保持电力系统连续供应?
银行作为金融领域的关键机构,依赖于高度可靠的电力供应,以保持银行操作的连续性。在电力中断或电力质量问题的情况下,银行可能面临严重的风险,包括数据丢失、交易中断和客户满意度下降。 UPS监控系统在这一背景下变得至关重要&…...
批量重命名文件夹:用数字随机重命名法管理您的文件夹
在文件管理中,文件夹的命名是一项至关重要的任务。一个好的文件夹命名方案可以帮助我们更高效地组织和查找文件。然而,随着时间的推移,我们可能会遇到文件夹数量过多,难以管理和查找的问题。为了解决这个问题,我们可以…...

RPC与HTTP的关系
首选理清楚关系 RPC与HTTP是两个不同维度的东西 HTTP 协议(Hyper Text Transfer Protocol),又叫做超文本传输协议,是一种传输协议,平时通过浏览器浏览网页网页,用到的就是 HTTP 协议。 而 RPC࿰…...

OpenCV #以图搜图:感知哈希算法(Perceptual hash algorithm)的原理与实验
1. 介绍 感知哈希算法(Perceptual Hash Algorithm,简称pHash) 是哈希算法的一种,主要用来做相似图片的搜索工作。 2. 原理 感知哈希算法(pHash)首先将原图像缩小成一个固定大小的像素图像,然后…...
Android多张图片rotation旋转角度叠加/重叠堆放
Android多张图片rotation旋转角度叠加/重叠堆放 <?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-auto"…...
HBuilderX 自定义语法提示
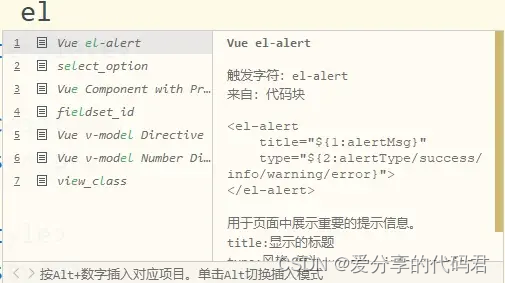
在开发实践中,会使用到各种第三方组件,比如Element UI,通常的做法是到官网中复制模板再在本地根据设计要求进行修改,或是从其它已经实现的组件中复制相似的内容。但每次复制粘贴确实比较麻烦。 在HBuilderx中可以设置代码块来创建…...

Leetcode—2562.找出数组的串联值【简单】
2023每日刷题(十四) Leetcode—2562.找出数组的串联值 实现代码 long long findTheArrayConcVal(int* nums, int numsSize){int left 0;int right numsSize - 1;long long sum 0;while(left < right) {if(left right) {sum nums[left];break;}…...

T0外部计数输入
/*----------------------------------------------- 内容:通过外部按键计数进入中断执行LED取反 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存器的…...
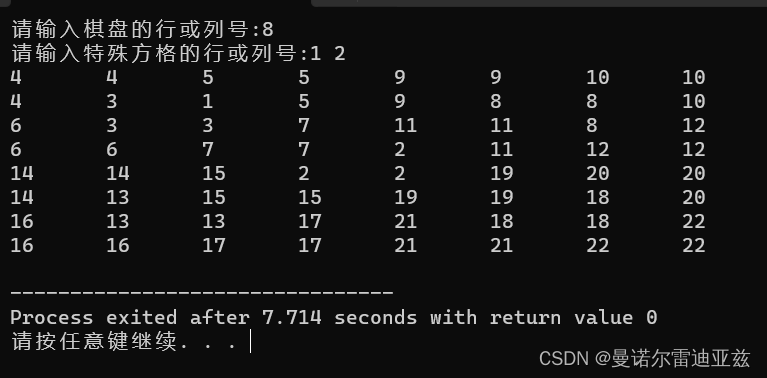
分治法求解棋盘覆盖问题
分治法求解棋盘覆盖问题 如何应用分治法求解棋盘覆盖问题呢?分治的技巧在于如何划分棋盘,使划分后的子棋盘的大小相同,并且每个子棋盘均包含一个特殊方格,从而将原问题分解为规模较小的棋盘覆盖问题。 基本思路 棋盘覆盖问题是…...

爱写bug的小邓程序员个人博客
博客网址: http://www.006969.xyz 欢迎来到我的个人博客,这里主要分享我对于前后端相关技术的学习笔记、项目实战经验以及一些技术感悟。 在我的博客中,你将看到以下主要内容: 技术文章 我将会分享我在学习前后端技术过程中的一些感悟&am…...

selenium判断元素可点击、可见、可选
1、判断元素是否可以点击 判断元素是否可以点击,WebElement对象调用is_enabled() is_enabled()方法返回一个布尔值,若可点击返回:True。若不可点击则返回:False from selenium import webdriver import time from selenium.web…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
