【数值计算方法】Gauss消元法及其Python/C实现
文章目录
- 一、基础理论
- 1. 线性方程组
- 2. Gauss消元法的详细步骤
- 3. 注意事项
- 二、具体计算过程
- 1. 用Gauss 消元法求A的LU分解,并由此求解方程组 Ax =b
- a. 将A进行LU分解。
- b. 使用LU分解求解方程组Ax=b
- 三、代码实现
- 1. Python代码实现
- 2. C语言代码实现
Gauss消元法,也称为高斯消元法或高斯-约当消元法,是一种用于求解线性方程组的数值方法。它是由德国数学家卡尔·弗里德里希·高斯在18世纪末发展起来的。
Gauss消元法的基本思想是通过一系列的行变换将线性方程组转化为一个上三角形的方程组,然后通过回代过程求解方程组的解。
一、基础理论
1. 线性方程组
线性方程组是由一组线性方程组成的方程集合。每个线性方程都可以表示为形如 “a₁x₁ + a₂x₂ + … + aₙxₙ = b” 的形式,其中 a₁, a₂, …, aₙ 是已知的常数,x₁, x₂, …, xₙ 是未知的变量,b 是已知的常数。方程中的每一项都是变量的一次幂与常数的乘积,且没有乘法运算符连接变量。
线性方程组可以包含多个线性方程,这些方程共同描述了一组变量的关系。解线性方程组就是找到满足所有方程的变量值,使得所有方程都成立。解线性方程组的目标是找到一组变量的值,使得方程组中的每个方程都得到满足。
线性方程组的解可以有多个或者没有解。如果存在至少一个满足所有方程的变量值组合,那么方程组有解。如果不存在这样的变量值组合,那么方程组无解。
解线性方程组的方法包括高斯消元法、矩阵法、克莱姆法则等。这些方法可以用于求解不同规模和形式的线性方程组。线性方程组在数学、物理、工程等领域中广泛应用,用于描述和解决各种实际问题。
2. Gauss消元法的详细步骤
- 将线性方程组写成增广矩阵的形式,即将系数矩阵和常数向量合并在一起。
- 选取第一个未知数的系数不为零的方程作为主元方程,如果没有这样的方程,则交换两行或者两列,使得主元系数不为零。
- 将主元方程的系数除以主元系数,使主元系数变为1。
- 用主元方程的系数乘以其他方程的主元系数,并将得到的结果从相应的方程中减去,以消除其他方程中的主元系数。
- 重复步骤2到步骤4,直到所有的未知数的系数都变为上三角形矩阵的形式。
- 进行回代过程,从最后一行开始,依次求解每个未知数的值。回代的过程是通过将已知的未知数代入到方程中,求解出未知数的值。
3. 注意事项
&emps;&emps;Gauss消元法的优点是可以精确地求解线性方程组,适用于任意个数的未知数和方程,在数值计算和科学工程领域有广泛的应用,然而,它也有一些限制和注意事项:
-
如果方程组的系数矩阵是奇异的(即行列式为零),则无法使用Gauss消元法求解。
-
在进行消元过程中,需要注意避免除以零的情况,如果遇到主元系数为零的情况,需要进行行交换或列交换。
-
如果方程组的系数矩阵很大,消元的计算量会很大,可能需要较长的计算时间。
二、具体计算过程
1. 用Gauss 消元法求A的LU分解,并由此求解方程组 Ax =b
A = [ [ 1 , 2 , 1 , − 2 ] , [ 2 , 5 , 3 , − 2 ] , [ − 2 , − 2 , 3 , 5 ] , [ 1 , 3 , 2 , 3 ] ] A=[ [1, 2, 1, -2], [2, 5, 3, -2], [-2, -2, 3, 5], [1, 3, 2, 3] ] A=[[1,2,1,−2],[2,5,3,−2],[−2,−2,3,5],[1,3,2,3]]
b = [ 2 , 8 , 4 , 9 ] b=[ 2, 8, 4, 9 ] b=[2,8,4,9]
a. 将A进行LU分解。
-
选取第一个未知数的系数不为零的方程作为主元方程,即第1行第1列元素不为零,因此选择第1行为主元方程。
-
将主元方程的系数除以主元系数,即第1行的所有元素除以1,得到:
1 2 1 -2
2 5 3 -2
-2 -2 3 5
1 3 2 3
- 用主元方程的系数乘以其他方程的主元系数,并将得到的结果从相应的方程中减去,以消除其他方程中的主元系数。对第2行、第3行和第4行进行消元操作:
1 2 1 -2
0 1 1 2
0 4 4 1
0 1 1 5
-
选择第二个未知数的系数不为零的方程作为主元方程,即第2行第2列元素不为零,因此选择第2行为主元方程。
-
将主元方程的系数除以主元系数,即第2行的所有元素除以1,得到:
1 2 1 -2
0 1 1 2
0 4 4 1
0 1 1 5
- 用主元方程的系数乘以其他方程的主元系数,并将得到的结果从相应的方程中减去,以消除其他方程中的主元系数。对第3行和第4行进行消元操作:
1 2 1 -2
0 1 1 2
0 0 0 -7
0 0 0 3
现在,我们得到了上三角形矩阵U和下三角形矩阵L:
U =
1 2 1 -2
0 1 1 2
0 0 0 -7
0 0 0 3L =
1 0 0 0
2 1 0 0
-2 -4 1 0
1 -1 -1 1
b. 使用LU分解求解方程组Ax=b
- 首先,根据LU分解,我们可以得到Ly=b,其中y是一个新的未知向量。
1 0 0 0 | y1 = 2
2 1 0 0 | y2 = 8
-2 -4 1 0 | y3 = 4
1 -1 -1 1 | y4 = 9
通过前向代入法,我们可以求解出y的值:
y1 = 2
y2 = 8 - 2y1 = 8 - 2(2) = 4
y3 = 4 - 2y1 + 4y2 = 4 - 2(2) + 4(4) = 18
y4 = 9 - y1 + y2 - y3 = 9 - 2 + 4 - 18 = -7
- 然后,根据LU分解,我们可以得到Ux=y,其中x是我们要求解的未知向量。
1 2 1 -2 | x1 = y1
0 1 1 2 | x2 = y2
0 0 0 -7 | x3 = y3
0 0 0 3 | x4 = y4
通过回代法,我们可以求解出x的值:
x1 = y1 = 2
x2 = y2 - x1 = 4 - 2 = 2
x3 = y3 / (-7) = 18 / (-7) ≈ -2.571
x4 = y4 / 3 = (-7) / 3 ≈ -2.333
因此,方程组Ax=b的解为x = [2, 2, -2.571, -2.333]。
三、代码实现
1. Python代码实现
import numpy as npA = np.array([[1, 2, 1, -2],[2, 5, 3, -2],[-2, -2, 3, 5],[1, 3, 2, 3]])b = np.array([2, 8, 4, 9])def gauss_elimination(A, b):n = len(A)for i in range(n-1):for j in range(i+1, n):factor = A[j, i] / A[i, i]A[j, i:] -= factor * A[i, i:]b[j] -= factor * b[i]return A, bdef back_substitution(U, y):n = len(U)x = np.zeros(n)x[-1] = y[-1] / U[-1, -1]for i in range(n-2, -1, -1):x[i] = (y[i] - np.dot(U[i, i+1:], x[i+1:])) / U[i, i]return xdef solve_linear_equations(A, b):U, y = gauss_elimination(A, b)x = back_substitution(U, y)return xx = solve_linear_equations(A, b)
print("Solution x:", x)
2. C语言代码实现
相关文章:

【数值计算方法】Gauss消元法及其Python/C实现
文章目录 一、基础理论1. 线性方程组2. Gauss消元法的详细步骤3. 注意事项 二、具体计算过程1. 用Gauss 消元法求A的LU分解,并由此求解方程组 Ax ba. 将A进行LU分解。b. 使用LU分解求解方程组Axb 三、代码实现1. Python代码实现2. C语言代码实现 Gauss消元法&#x…...

ins老被封禁?快来看看这些雷区你踩了没!
做外贸的小伙伴应该都运营或者接触过Instagram,但是忽视平台规则和操作不当很容易出现ins被封号的情况,今天就给大家介绍ins封禁原因,大家在运营过程中就可以很好避免了! Instagram 封禁原因 1.短时间内大量关注和点赞操作 为了封…...
)
《Effective Java》读书笔记(1-2章)
第一章 创建和销毁对象 1. 考虑用静态代替构造方法 想要获取一个类的实例,一种传统的方式是通过共有的构造器,当然还可以使用另一种技术:提供共有的静态工厂方法。 什么是静态工厂? public static Boolean valueOf(boolean b) …...
函数)
C++版split(‘_‘)函数
目录 1 使用stringstream2 使用双指针算法 1 使用stringstream #include <iostream> #include <sstream> #include <string> #include <vector>using namespace std;vector<string> split(string str, char separator) {vector<string> …...

Leaky singletons的一种使用场景
Leaky singletons的一种使用场景 文章目录 Leaky singletons的一种使用场景场景问题本质如何解决Leaky singletons 场景 最近遇到了这个问题,正好想记录下。 比如你有一段代码,如下(伪代码): static std::map<int…...

TensorFlow图像多标签分类实例
接下来,我们将从零开始讲解一个基于TensorFlow的图像多标签分类实例,这里以图片验证码为例进行讲解。 在我们访问某个网站的时候,经常会遇到图片验证码。图片验证码的主要目的是区分爬虫程序和人类,并将爬虫程序阻挡在外。 下面…...

Python程序设计期末复习笔记
文章目录 一、数据存储1.1 倒计时1.2 os库1.3 字符串操作1.4 文件操作1.5 列表操作1.6 元组1.7 字典 二、文本处理及可视化2.1 jieba分词2.2 集合操作2.3 pdf文件读取2.4 参数传递2.5 变量作用域 三、数据处理分析3.1 Sumpy3.2 Matplotlib3.3 Numpy 四、Pandas4.1 索引操作4.2 …...

人大与加拿大女王大学金融硕士—与您共创辉煌
生活的本质就是有意识的活着,而生活的智慧就是活出了自己想要的样子,那些真正厉害的人,从来都在默默努力,伴随着金融人才的需求日益增长,中国人民大学与加拿大女王大学联合推出了人大女王金融硕士项目,旨在…...
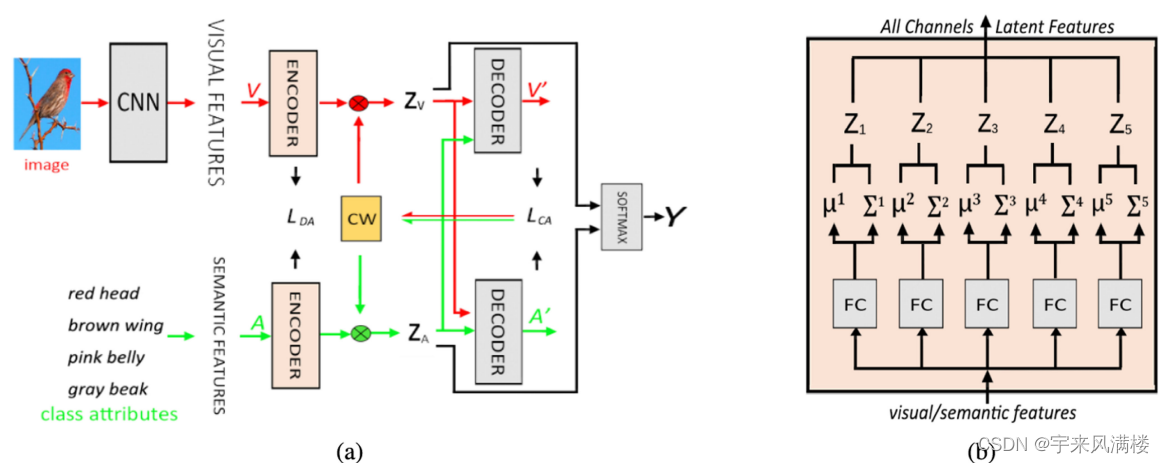
Generalized Zero-Shot Learning With Multi-Channel Gaussian Mixture VAE
L D A _{DA} DA最大化编码后两种特征分布之间的相似性 辅助信息 作者未提供代码...
)
10.30 知识总结(标签分类、css介绍等)
一、 标签的分类 1.1 单标签 img br hr <img /> 1.2 双标签 a h p div <a></a> 1.3 按照标签属性分类 1.3.1 块儿标签 即自己独自占一行 h1-h6 p div 1.3.2 行内(内联)标签 即自身文本有多大就占多大 a span u i b s 二、 标签的嵌套 标签之间是可以互相…...
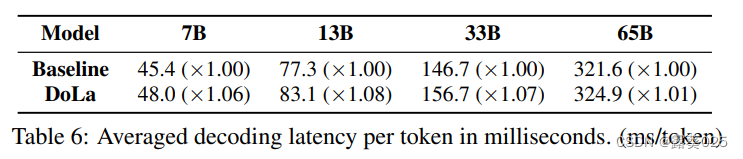
DoLa:对比层解码提高大型语言模型的事实性
DoLa:对比层解码提高大型语言模型的事实性 摘要1 引言2 方法2.1 事实知识在不同层级上演化2.2 动态早期层选择2.3 预测对比 3 实验3.1 任务3.2 实验设置3.3 多项选择3.3.1 TruthfulQA:多项选择3.3.2 FACTOR:维基、新闻 3.4 开放式文本生成3.4…...

解决由于找不到mfc140u.dll无法继续执行此代码问题的4个方法
mfc140u.dll是Microsoft Foundation Class(微软基础类库)中的一个动态链接库文件,它包含了许多用于实现Windows应用程序的基本功能。当我们在编写或运行基于MFC的程序时,如果系统中缺少这个文件,就会出现“找不到mfc14…...

MySQL高性能优化规范建议
当涉及到MySQL数据库的性能优化时,有许多方面需要考虑。以下是一些通用的MySQL性能优化规范建议: 合适的索引: 确保表中的字段使用了适当的索引。这能大幅提升检索速度。但避免过多索引,因为它会增加写操作的成本。 优化查询语句…...
pytorch 入门 (五)案例三:乳腺癌识别-VGG16实现
本文为🔗小白入门Pytorch内部限免文章 🍨 本文为🔗小白入门Pytorch中的学习记录博客🍦 参考文章:【小白入门Pytorch】乳腺癌识别🍖 原作者:K同学啊 在本案例中,我将带大家探索一下深…...

vue中electron与vue通信(fs.existsSync is not a function解决方案)
electron向vue发送消息 dist/main.js (整个文件配置在另一条博客里) win new BrowserWindow({width:1920,height:1080,webPreferences: {// 是否启用Node integrationnodeIntegration: true, // Electron 5.0.0 版本之后它将被默认false// 是否在独立 JavaScript 环境中运行…...

LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks翻译
论文《LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks》翻译 LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks翻译...

文件类漏洞总结, 文件包含, 文件上传, 文件下载
文件类漏洞总结 一, 文件包含 1. 文件包含绕过 实际环境中不是都是像$_GET[file]; incude $file 这样直接把变量传入包含函数的。 在很多时候包含的变量文件不是完全可控的,比如下面这段代码指定了前缀和后缀: <?php $file S_GET[filename]; include /opt/…...

SpringBoot篇---第四篇
系列文章目录 文章目录 系列文章目录一、springboot常用的starter有哪些二、 SpringBoot 实现热部署有哪几种方式?三、如何理解 Spring Boot 配置加载顺序? 一、springboot常用的starter有哪些 spring-boot-starter-web 嵌入tomcat和web开发需要servlet…...
 -- 在不同版本SpringBoot,选用不同的Knife4j相关的jar包)
Knife4j使用教程(一) -- 在不同版本SpringBoot,选用不同的Knife4j相关的jar包
目录 1. Knife4j的项目背景 2. Knife4j的选择 2.1 选用 Spring Boot 版本在 2.4.0~3.0.0之间 2.2 选用 Spring Boot 版本在 3.0.0之上...
Octave Convolution学习笔记 (附代码)
论文地址:https://export.arxiv.org/pdf/1904.05049 代码地址:https://gitcode.com/mirrors/lxtgh/octaveconv_pytorch/overview?utm_sourcecsdn_github_accelerator 1.是什么? OctaveNet网络属于paper《Drop an Octave: Reducing Spatia…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
