数据结构(超详细讲解!!)第十八节 串(KMP算法)
1.BF算法
算法在字符比较不相等,需要回溯(即i=i-j+1):即退到s中的下一个字符开始进行继续匹配。
最好情况下的时间复杂度为O(m)。
最坏情况下的时间复杂度为O(n×m)。
平均的时间复杂度为O(n×m)。
2.KMP算法
KMP算法是D.E.Knuth、J.H.Morris和V.R.Pratt共同提出的,简称KMP算法。
该算法较BF算法有较大改进,主要是消除了主串指针的回溯,从而使算法效率有了某种程度的提高。
设串s的长度为n,串t长度为m。
在KMP算法中求next数组的时间复杂度为O(m),在后面的匹配中因主串s的下标不减即不回溯,比较次数可记为n,所以KMP算法平均时间复杂度为O(n+m)。
最坏的时间复杂度为O(n × m)。
int KMPIndex(SqString s,SqString t)
{ int next[MaxSize], i=0, j=0;GetNext(t,next);while (i<s.length && j<t.length) { if (j==-1 || s.data[i]==t.data[j]) { i++;j++; //i、j各增1}else j=next[j]; //i不变,j后退}if (j>=t.length)return(i-t.length); //返回匹配模式串的首字符下标elsereturn(-1); /由模式串t求next值的算法:
void GetNext(SString t,int next[])
{ int j, k;j=0; k=-1; next[0]=-1;while (j<t.length-1){ if (k==-1 || t.data[j]==t.data[k]){ j++; k++;next[j]=k;}else k=next[k];}
}
相关文章:
第十八节 串(KMP算法))
数据结构(超详细讲解!!)第十八节 串(KMP算法)
1.BF算法 算法在字符比较不相等,需要回溯(即ii-j1):即退到s中的下一个字符开始进行继续匹配。 最好情况下的时间复杂度为O(m)。 最坏情况下的时间复杂度为O(nm)。 平均的时间复杂度为O(nm)。 2.KMP算法 KMP算法是D.E.Knuth、…...

软考_软件设计师
算法: 1、直接插入排序 详解:https://blog.csdn.net/qq_44616044/article/details/115708056 void insertSort(int data[],int n){int i,j,temp;for(i1;i<n;i){if(data[i]<data[i-1]){temp data[i];data[i] data[i-1];for(ji-1;j>0&&am…...

大数据之LibrA数据库系统告警处理(ALM-12004 OLdap资源异常)
告警解释 当Manager中的Ldap资源异常时,系统产生此告警。 当Manager中的Ldap资源恢复,且告警处理完成时,告警恢复。 告警属性 告警参数 对系统的影响 Ldap资源异常,Manager和组件WebUI认证服务不可用,无法对Web上层…...
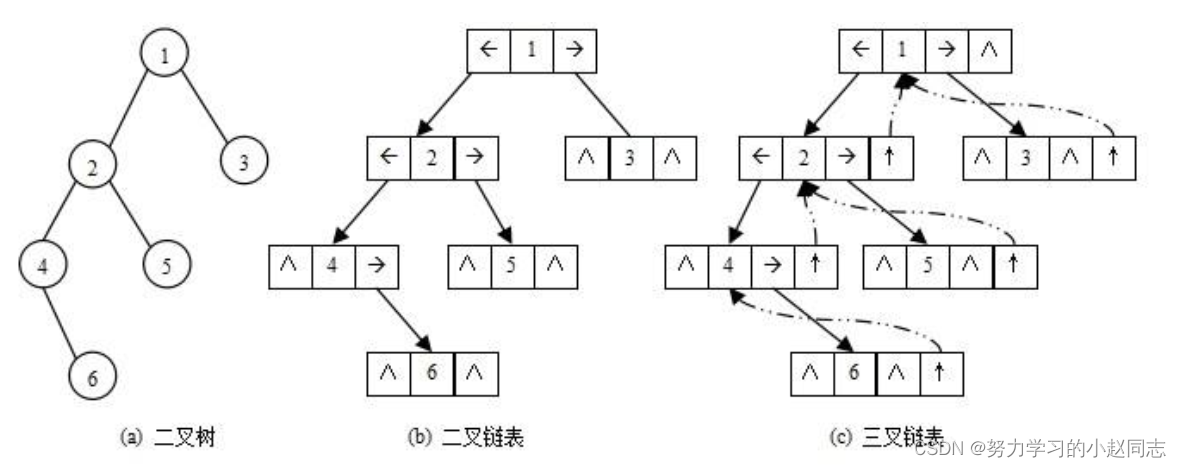
详解—数据结构《树和二叉树》
目录 一.树概念及结构 1.1树的概念 1.2树的表示 二.二叉树的概念及结构 2.1概念 2.2二叉树的特点 2.3现实中的二叉树 2.4数据结构中的二叉树 2.5 特殊的二叉树 2.6二叉树的存储结构 2.6.1二叉树的性质 2.6.2 顺序结构 2.6.3链式存储 三. 二叉树的链式结构的遍历 …...
菜单管理中icon图标回显
<el-table-column prop"icon" label"图标" show-overflow-tooltip algin"center"><template v-slot"{ row }"><el-icon :class"row.icon"></el-icon></template></el-table-column>...

Postman如何导出接口的几种方法
本文主要介绍了Postman如何导出接口的几种方法,文中通过示例代码介绍的非常详细,具有一定的参考价值,感兴趣的小伙伴们可以参考一下 前言: 我的文章还是一贯的作风,简确用风格(简单确实有用)&…...
Java进阶(Set)——面试时Set常见问题解读 结合源码分析
前言 List、Set、HashMap作为Java中常用的集合,需要深入认识其原理和特性。 本篇博客介绍常见的关于Java中Set集合的面试问题,结合源码分析题目背后的知识点。 关于List的博客文章如下: Java进阶(List)——面试时L…...

【强化学习】12 —— 策略梯度(REINFORCE )
文章目录 前言策略梯度基于策略的强化学习的优缺点Example:Aliased Gridworld策略目标函数策略优化策略梯度利用有限差分计算策略梯度得分函数和似然比策略梯度定理蒙特卡洛策略梯度(Monte-Carlo Policy Gradient)Puck World Example Softmax随机策略 代…...

Kubernetes Taint(污点) 和 Toleration(容忍)
Author:rab 目录 前言一、Taint(污点)1.1 概述1.2 查看节点 Taint1.3 标记节点 Taint1.4 删除节点 Taint 二、Toleration(容忍) 前言 Kubernetes 中的污点(Taint)和容忍(Toleration…...

使用cv::FileStorage时出错 Can‘t open file: yaml‘ in read mode
1. 使用说明 在做的一个c工程项目,想加一个配置文件,我发现主要有两种主流的方式, (1)opencv有cv::FileStorage这样的一个函数可以使用。 (2)也可以使用cpp-yaml GitHub - jbeder/yaml-cpp: …...

代码之困:那些让你苦笑不得的bug
在编写代码的过程中,我们常常会遇到各种各样的bug。有的时候,我们花费了大量的时间和精力去寻找问题的根源,但却找不到任何线索。然而,令人哭笑不得的是,有时候这些问题的解决方案却是如此简单,以至于我们不…...

【C语言初学者周冲刺计划】2.2用选择法对10个整数从小到大排序
目录 1解题思路: 2代码如下: 3运行结果: 4总结: 1解题思路: 首先利用一维数组和循环语句输入10个整数,然后利用双循环的嵌套进行比较大小,最后输出结果; 2代码如下: #include&…...

c++系列——智能指针
1.智能指针的使用及原理 1.1 RAII RAII(Resource Acquisition Is Initialization)是一种利用对象生命周期来控制程序资源(如内 存、文件句柄、网络连接、互斥量等等)的简单技术。 在对象构造时获取资源,接着控制对资…...

力扣日记10.30-【栈与队列篇】滑动窗口最大值
力扣日记:【栈与队列篇】滑动窗口最大值 日期:2023.10.30 参考:代码随想录、力扣 239. 滑动窗口最大值 题目描述 难度:困难 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只…...

docker与宿主机共享内存通信
docker与宿主机共享内存通信 docker中的进程要与宿主机使用共享内存通信,需要在启动容器的时候指定“–ipchost”选项。然后再编写相应的共享内存的程序,一个跑在宿主机上,另一个跑在docker上面。 宿主机程序准备 shm_data.h #ifndef _SH…...
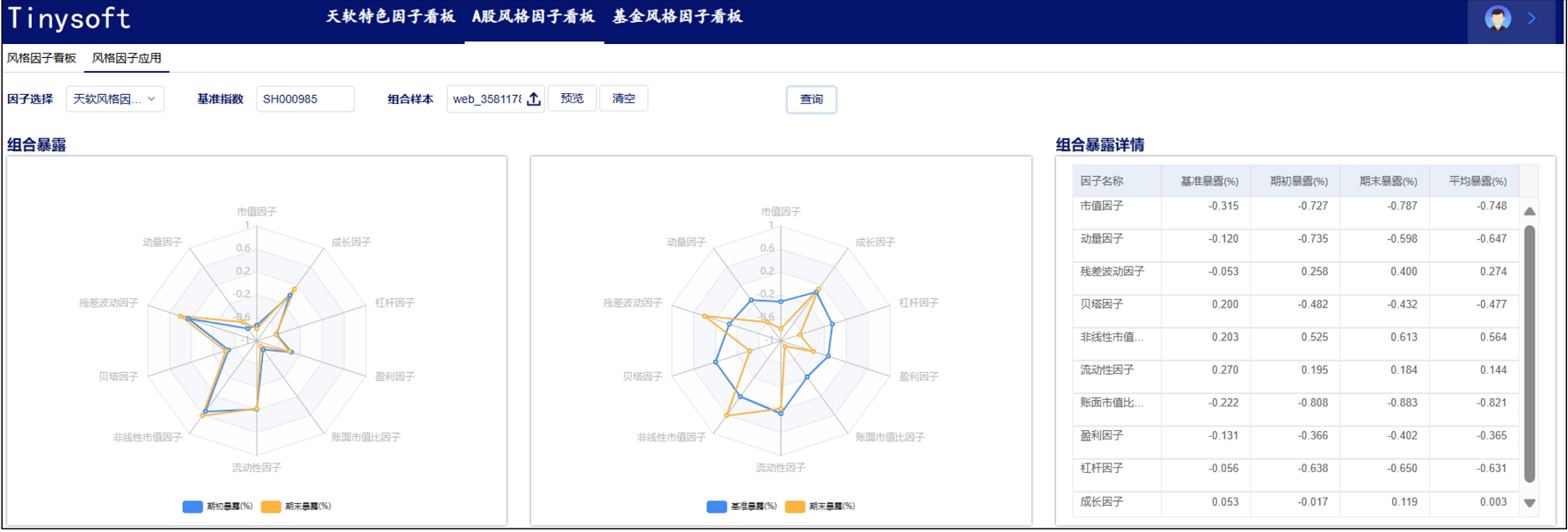
A股风格因子看板 (2023.10 第13期)
该因子看板跟踪A股风格因子,该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子,用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第13期,指数组合数据截止日2023-09-30,要点如下 近1年A股风格因子检验统…...

ORB-SLAM3算法2之EuRoc、TUM和KITTI开源数据集运行ORB-SLAM3生成轨迹并用evo工具评估轨迹
文章目录 0 引言1 数据和真值1.1 TUM1.2 EuRoc1.3 KITTI2 ORB-SLAM3的EuRoc示例2.1 纯单目的示例2.2 纯单目的轨迹评估2.3 纯双目的示例2.4 纯双目的轨迹评估2.5 单目和IMU的示例2.6 单目和IMU的轨迹评估2.7 双目和IMU的示例2.8 双目和IMU的轨迹评估2.9 前四种的评估结果对比3 …...

【蓝桥杯选拔赛真题07】C++小球自由落体 青少年组蓝桥杯C++选拔赛真题 STEMA比赛真题解析
目录 C/C++小球自由落体 一、题目要求 1、编程实现 2、输入输出 二、算法分析...

期中考成绩一键私发
作为一名教师,期中考试后最繁忙的事情之一就是发布成绩。每个学生都希望尽快知道自己的成绩,而作为老师,我们需要一种更高效、更方便的方式来完成这项任务。今天,我就来给大家介绍一种成绩查询系统,让我们一起告别繁琐…...
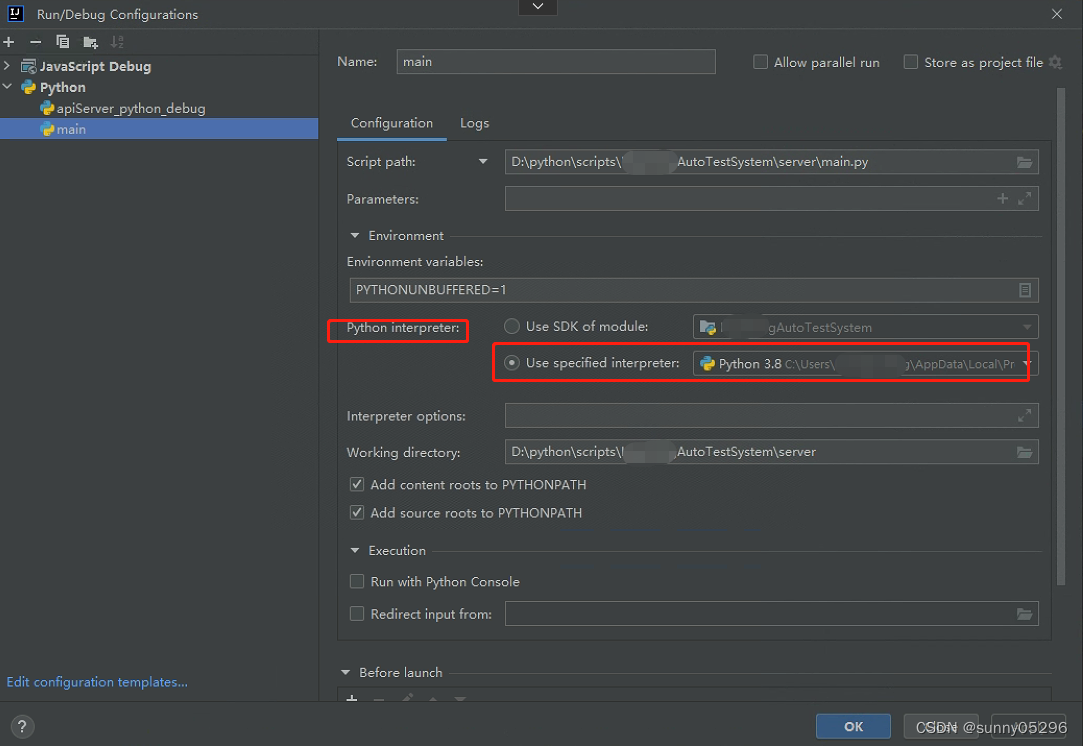
idea中Run/Debug Python项目报错 Argument for @NotNull parameter ‘module‘ of ...
idea中Run/Debug Python项目报错 Argument for NotNull parameter module of ... idea中运行Python项目main.py时报错: Error running main: Argument for NotNull parameter module of com/intellij/openapi/roots/ModuleRootManager.getInstance must not be nu…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
