数据结构和算法——用C语言实现所有图状结构及相关算法
文章目录
- 前言
- 图的基本概念
- 图的存储方式
- 邻接矩阵
- 邻接表
- 十字链表
- 临界多重表
- 图的遍历
- 最小生成树
- 普里姆算法(Prim)
- 克鲁斯卡尔算法(Kruskal)
- 最短路径
- BFS求最短路径
- 迪杰斯特拉算法(Dijkstra)
- 弗洛伊德算法(Floyd)
- 有向无环图
- AOV网的拓扑结构
- 拓扑排序
- 逆拓扑排序
- AOE网的关键路径
前言
本文所有代码均在仓库中,这是一个完整的由纯C语言实现的可以存储任意类型元素的数据结构的工程项目。

- 首先是极好的工程意识,该项目是一个中大型的CMake项目,结构目录清晰,通过这个项目可以遇见许多工程问题并且可以培养自己的工程意识。
- 其次是优秀的封装性(每个数据结构的头文件中只暴漏少量的信息),以及优秀的代码风格和全面的注释,通过这个项目可以提升自己的封装技巧:
- 异常处理功能:在使用C语言编写代码的时候不能使用类似Java的异常处理机制是非常难受的,所以我也简单实现了一下。详情可看在C语言中实现类似面向对象语言的异常处理机制
最后也是最重要的一点,数据结构的通用性和舒适的体验感,下面以平衡二叉树为例:
- 第一步:要想使用平衡二叉树,只需要引入其的头文件:
#include "tree-structure/balanced-binary-tree/BalancedBinaryTree.h"
- 第二步:定义自己任意类型的数据,并构造插入数据(以一个自定义的结构体为例):
#include "tree-structure/balanced-binary-tree/BalancedBinaryTree.h"int dataCompare(void *, void *);typedef struct People {char *name;int age;
} *People;int main(int argc, char **argv) {struct People dataList[] = {{"张三", 15},{"李四", 3},{"王五", 7},{"赵六", 10},{"田七", 9},{"周八", 8},};BalancedBinaryTree tree = balancedBinaryTreeConstructor(NULL, 0, dataCompare);for (int i = 0; i < 6; ++i) {balancedBinaryTreeInsert(&tree, dataList + i, dataCompare);}return 0;
}/*** 根据人的年龄比较*/
int dataCompare(void *data1, void *data2) {int sub = ((People) data1)->age - ((People) data2)->age;if (sub > 0) {return 1;} else if (sub < 0) {return -1;} else {return 0;}
}
- 第三步:打印一下平衡二叉树:
#include "tree-structure/balanced-binary-tree/BalancedBinaryTree.h"int dataCompare(void *, void *);void dataPrint(void *);typedef struct People {char *name;int age;
} *People;int main(int argc, char **argv) {struct People dataList[] = {{"张三", 15},{"李四", 3},{"王五", 7},{"赵六", 10},{"田七", 9},{"周八", 8},};BalancedBinaryTree tree = balancedBinaryTreeConstructor(NULL, 0, dataCompare);for (int i = 0; i < 6; ++i) {balancedBinaryTreeInsert(&tree, dataList + i, dataCompare);balancedBinaryTreePrint(tree, dataPrint);printf("-------------\n");}return 0;
}/*** 根据人的年龄比较*/
int dataCompare(void *data1, void *data2) {int sub = ((People) data1)->age - ((People) data2)->age;if (sub > 0) {return 1;} else if (sub < 0) {return -1;} else {return 0;}
}/*** 打印人的年龄* @param data*/
void dataPrint(void *data) {People people = (People) data;printf("%d", people->age);
}
打印的结果如下:

最后期待大佬们的点赞。
图的基本概念
图 G G G由顶点集 V V V和边集 E E E组成,记为:
G = ( V , E ) G=(V,E) G=(V,E)
若 V = { v 1 , v 2 , … , v n } V=\{v_1,v_2,\dots,v_n\} V={v1,v2,…,vn}则用 ∣ V ∣ |V| ∣V∣表示图 G G G中顶点的个数,也称为图 G G G的阶;若 E = { ( a , b ) ∣ a ∈ V , b ∈ V } E=\{(a,b)|a\in V,b\in V\} E={(a,b)∣a∈V,b∈V}则用 ∣ E ∣ |E| ∣E∣表示图 G G G中边的条数。不存在空图,即一个图的点集是非空的。图的分类如下:
- 无向图:若 E E E为无向边(简称边)的有限集合,则 G G G为无向图。
- 0 < ∣ E ∣ < ∣ V ∣ ( ∣ V ∣ − 1 ) 2 0<|E|<\frac{|V|(|V|-1)}{2} 0<∣E∣<2∣V∣(∣V∣−1)
- 有向图:若 E E E为有向边(简称弧)的有限集合,则 G G G为有向图.
- 0 < ∣ E ∣ < ∣ V ∣ ( ∣ V ∣ − 1 ) 0<|E|<|V|(|V|-1) 0<∣E∣<∣V∣(∣V∣−1)
- 简单图和多重图:如果一个图不存在重复边和顶点到自身的边,那么称图为简单图,否则称为多重图。
图有关的术语如下:
-
顶点的度、入度和出度:
- 对于无向图而言:
- 顶点 v v v的度是指依附于该顶点的边的数目,记为 T D ( v ) TD(v) TD(v)
- ∑ i = 1 n T D ( v i ) = 2 ∣ E ∣ \sum_{i=1}^n TD(v_i)=2|E| i=1∑nTD(vi)=2∣E∣
- 对于有向图而言:
- 入度是指以顶点 v v v为终点的弧的数目,记为 I D ( v ) ID(v) ID(v);
- 出度是以顶点为起点的弧的数目,记为 O D ( v ) OD(v) OD(v);
- 顶点 v v v的度等于其入度和出度之和。
- ∑ i = 1 n I D ( v i ) = ∑ i = 1 n O D ( v i ) = ∣ E ∣ \sum_{i=1}^n ID(v_i)=\sum_{i=1}^n OD(v_i)=|E| i=1∑nID(vi)=i=1∑nOD(vi)=∣E∣
- 对于无向图而言:
-
路径、路径长度和回路:
- 从一个顶点到另一个顶点之间经过的所有顶点的序列称为路径;
- 起点和终点为同一个顶点的路径称为回路。
-
简单路径和简单回路:
- 顶点不重复的路径称为简单路径;
- 除第一个和最后一个顶点外,其余顶点不重复的回路称为简单回路。
-
路径长度:路径上边的数目称为路径长度。
-
距离:两个顶点之间的最短路径长度称为距离,路径不存在则距离为无穷。
-
连通、连通图和连通分量:
- 在无向图中,两个不同顶点之间存在至少一条路径,则称这两个顶点是连通的。若图中任意两个顶点都是连通的,则称该图为连通图,否则称为非连通图;
- 无向图中的极大连通子图称为连通分量。
- 若图是连通的,则 ∣ E ∣ ≥ ∣ V ∣ − 1 |E|\geq|V|-1 ∣E∣≥∣V∣−1
- 若图是非连通的,则 ∣ E ∣ ≤ C ∣ V ∣ − 1 2 |E|\leq C^2_{|V|-1} ∣E∣≤C∣V∣−12
-
强连通图和强连通分量:
- 在有向图中,两个不同顶点之间存在至少一条路径,则称这两个顶点是强连通的。若图中任意两个顶点都是连通的,则称该图为强连通图,否则称为非强连通图;
- 有向图中的极大连通子图称为强连通分量。
- 若图是连通的,则 ∣ E ∣ ≥ ∣ V ∣ |E|\geq|V| ∣E∣≥∣V∣
-
子图和生成子图:
- 顶点集和边集分别是某图顶点集和边集子集的图称为某图的子图。
- 包含某图所有顶点的子图称为生成子图。
-
完全图:任意两个顶点之间都有一条边相连的图称为完全图。
- 对于无向图而言, 0 ≤ ∣ E ∣ ≤ C ∣ V ∣ 2 0\leq|E|\leq C^2_{|V|} 0≤∣E∣≤C∣V∣2
- 对于有向图而言, 0 ≤ ∣ E ∣ ≤ 2 C ∣ V ∣ 2 0\leq |E|\leq 2C^2_{|V|} 0≤∣E∣≤2C∣V∣2
-
连通图的生成树和非连通图的生成森林:
- 包含所有顶点的极小连通子图称为连通图的生成树。
- 连通分量的生成树称为非连通图的生成森林。
-
边的权、网和带权路径长度:
- 为每条边标记的具有一定意义的数值称为边的权值
- 边上带有权值的图称为网
- 一条路径上所有边的权值之和称为该路径的带权路径长度
-
树和有向树:
- 不存在回路且连通的无向图称为树
- 一个顶点的入度为零,其余顶点的入度均为一的有向图称为有向树。
图的存储方式
图一般有以下几种存储方式:
- 邻接矩阵法
- 邻接表法
- 十字链表法
- 邻接多重表
邻接矩阵
邻接矩阵法用一个一维数组存储图中的顶点信息,用一个二维数组存储图中边的信息(即顶点之间的邻接关系),这个二维数组就是邻接矩阵。邻接矩阵法适合存储稠密图。
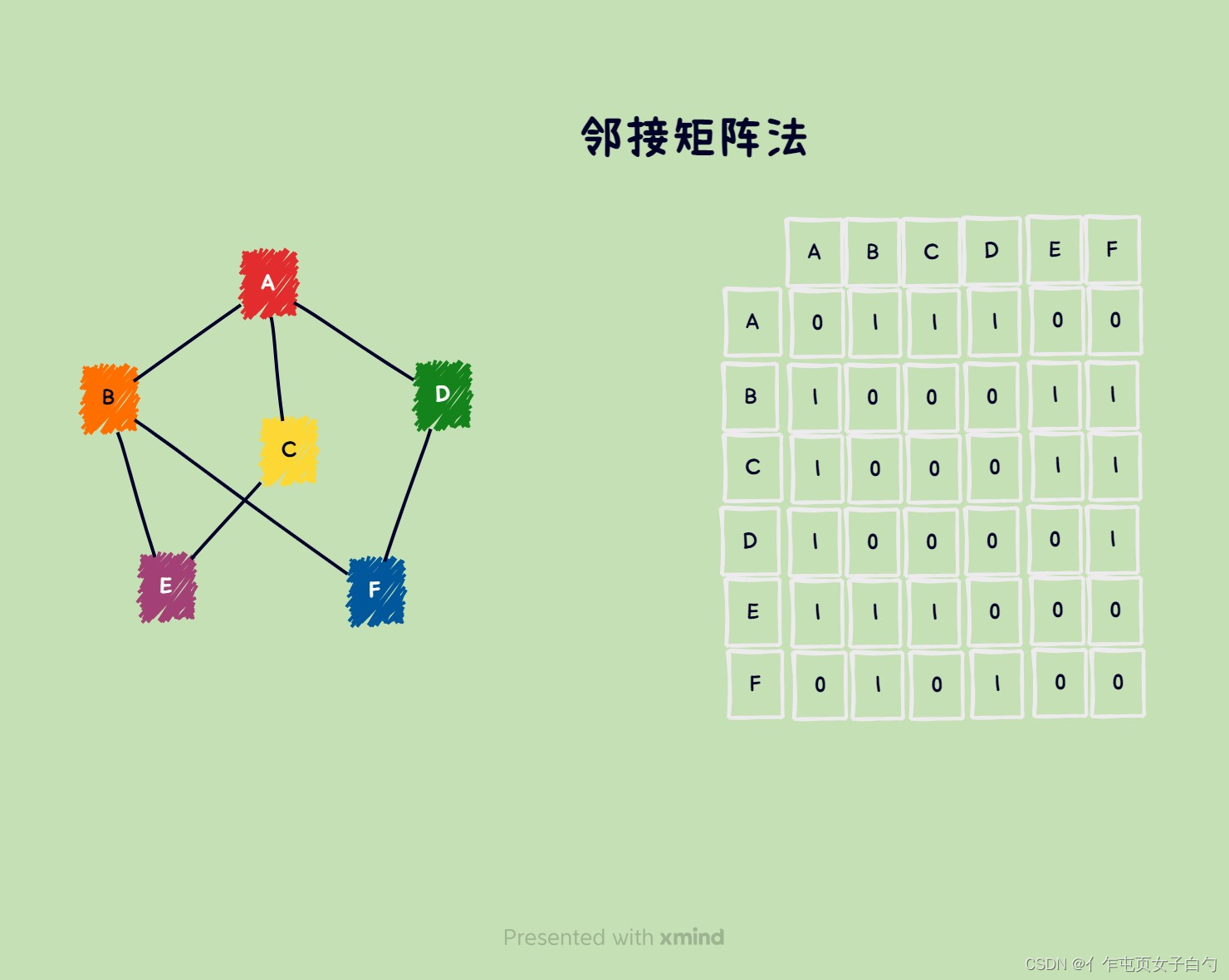
struct AdjacentMatrixGraph {void **vertexList;int **edgeMatrix;int vertexCount;int edgeCount;int size;int (*compare)(void *, void *);
};
对于图而言:
- e d g e M a t r i x [ i ] [ j ] = { 1 若 ( v i , v j ) 或 ( v j , v i ) 是 G 的边 0 若 ( v i , v j ) 或 ( v j , v i ) 不是 G 的边 edgeMatrix[i][j]= \begin{cases} 1&若(v_i,v_j)或(v_j,v_i)是G的边\\ 0&若(v_i,v_j)或(v_j,v_i)不是G的边 \end{cases} edgeMatrix[i][j]={10若(vi,vj)或(vj,vi)是G的边若(vi,vj)或(vj,vi)不是G的边
- 无向图的邻接矩阵是一个对称矩阵,因此在存储时可以使用压缩矩阵存储。
对于网而言:
- e d g e M a t r i x [ i ] [ j ] = { 权值 若 ( v i , v j ) 或 ( v j , v i ) 是 G 的边 0 或 ∞ 若 ( v i , v j ) 或 ( v j , v i ) 不是 G 的边 edgeMatrix[i][j]= \begin{cases} 权值&若(v_i,v_j)或(v_j,v_i)是G的边\\ 0或\infty&若(v_i,v_j)或(v_j,v_i)不是G的边 \end{cases} edgeMatrix[i][j]={权值0或∞若(vi,vj)或(vj,vi)是G的边若(vi,vj)或(vj,vi)不是G的边
邻接表
邻接表法为每个顶点建立一个单链表,这个链表中的结点表示依附于该顶点的边,这个单链表称为顶点的边表。邻接表法适合存储稀疏图。
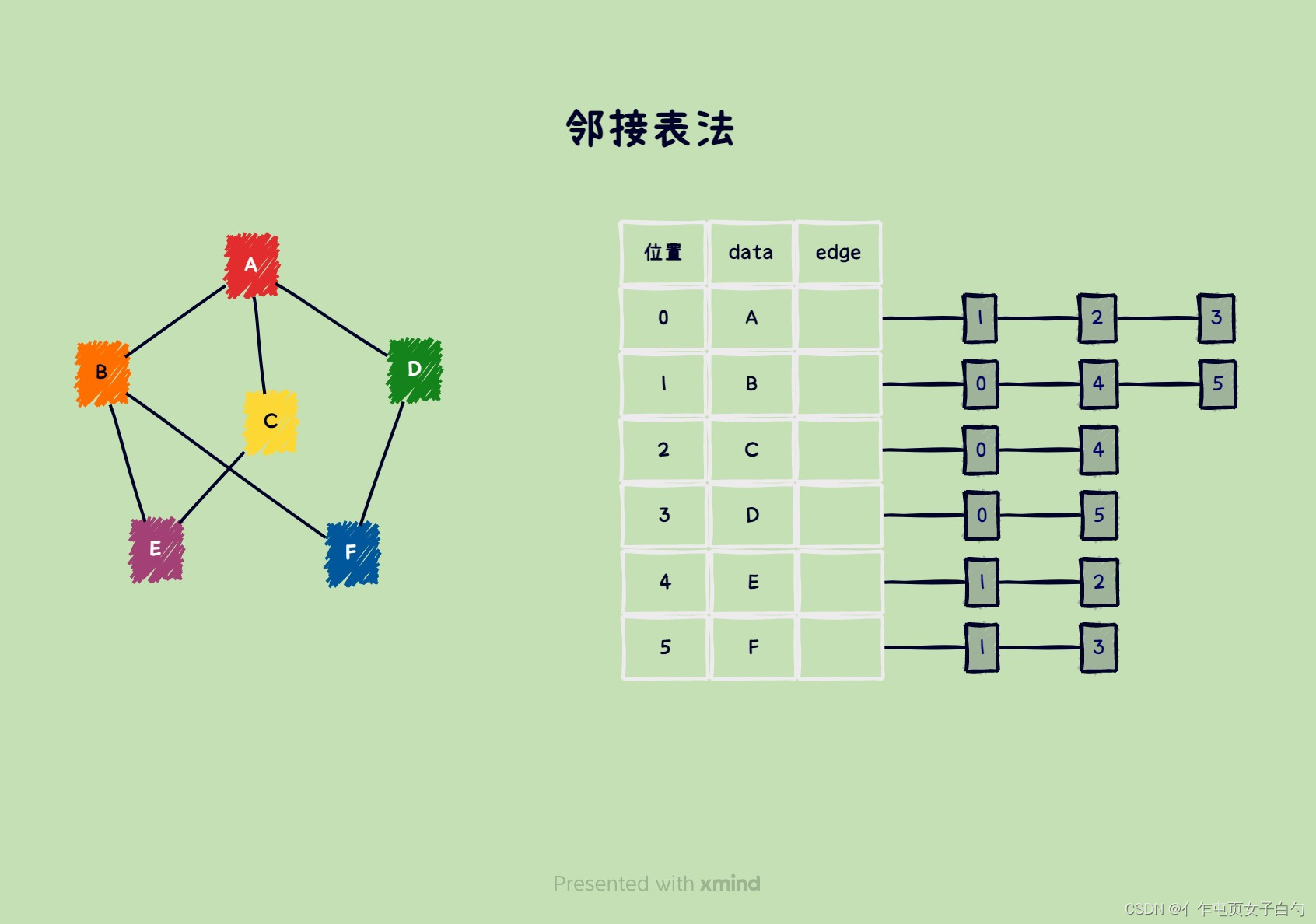
typedef struct Edge {int weight;int vertexIndex;struct Edge *next;
} *Edge;typedef struct Vertex {void *data;Edge firstEdge;
} *Vertex, *VertexList;struct AdjacentListGraph {VertexList *vertexList;int vertexCount;int edgeCount;int size;int (*compare)(void *, void *);
};
十字链表
十字链表法是有向图的一种链式存储结构,一个十字链表可以唯一确定一个图。
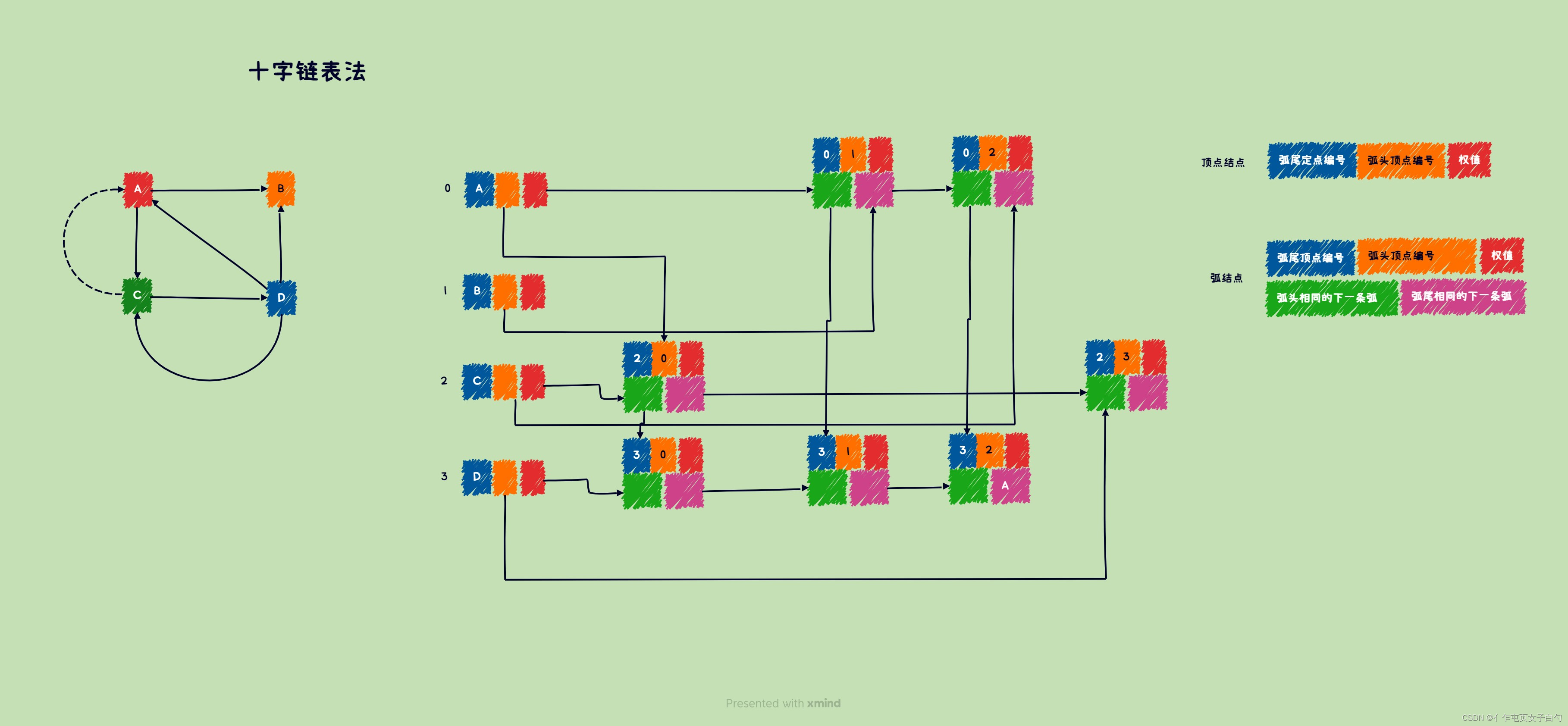
typedef struct ArcNode{ArcType data;int tailVex; //弧头顶点位置int headVex; //弧尾顶点位置int headLink; //弧头相同的下一条弧int tailLink; //弧尾相同的下一条弧
}ArcNode;typedef struct VexNode {VertexType data;ArcNode * firstIn; //以该顶点为弧头的第一个弧顶点ArcNode * firstOut; //以该顶点为为弧尾的第一个弧顶点
}VexNode,* VexList;typedef struct OLGraph{VexList vexList;int vexNum;int arcNum;
}* OLGraph;
临界多重表
邻接多重表是无向图的一种链式存储结构。
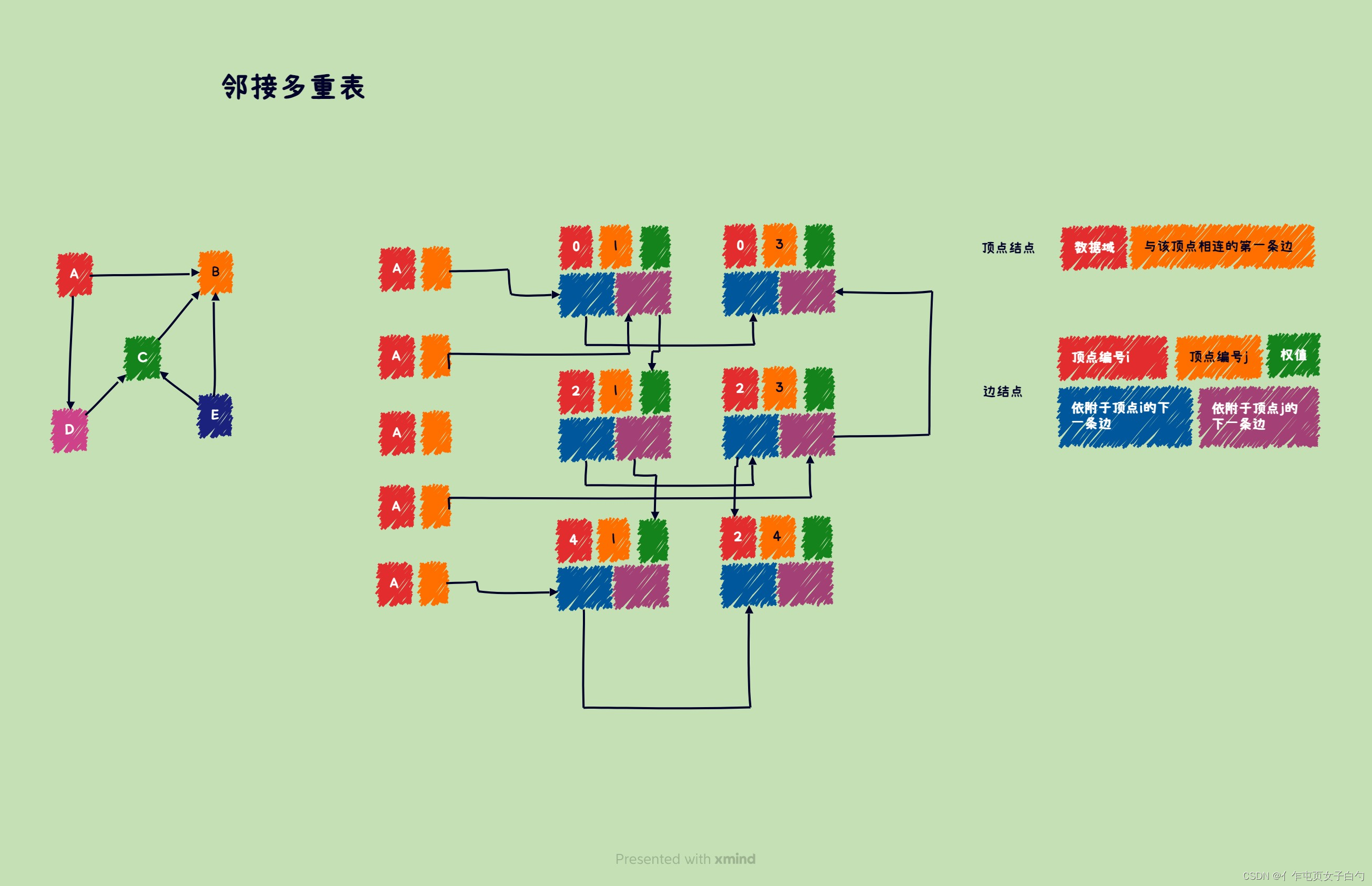
typedef struct EdgeNode {bool mark; //是否被搜搜过int iVex; //该边依附的一个顶点位置int jVex; //该边依附的另一个顶点位置int iLink; //下一个依附顶点iVex的边int jLink; //下一个依附顶点jVex的边
} EdgeNode;typedef struct VexNode {VexType data;EdgeNode *firstEdge; //第一个依附该顶点的边
} VexNode, *VexList;typedef struct AMLGraph {VexList vexList;int vexNum;int edgeNum;
} *AMLGraph;
图的遍历
图的遍历是指从图中的某一顶点出发,按照某种搜索方法沿着图中的边对图中的所有顶点访问一次且仅访问一次的过程。图的遍历方式主要有以下两种:
- 广度优先搜索(BFS):
- 从图的某一顶点出发,依次访问该顶点的所有邻接顶点;
- 再从这些访问过的邻接顶点出发,依次访问它们的邻接顶点,直到图中所有顶点都被访问为止;
- 若图中还有顶点尚未被访问,则选择一个尚未被访问的顶点重复上述过程。
void BFS(AdjacentListGraph graph, bool isVisited[], LinkedQueue queue, LinkedQueue BFSDataQueue) {while (!linkedQueueIsEmpty(queue)) {Vertex vertex = linkedQueueDeQueue(queue);linkedQueueEnQueue(BFSDataQueue, vertex->data);isVisited[getVertexIndex(graph, vertex->data) - 1] = true;for (Vertex j = firstVertex(graph, vertex->data); j != NULL; j = nextVertex(graph, vertex->data, j->data)) {if (!isVisited[getVertexIndex(graph, j->data) - 1]) {linkedQueueEnQueue(queue, j);}}}
}/*** 广度优先遍历* @param graph* @param BFSDataQueue*/
void BFSTraverse(AdjacentListGraph graph, void *data, LinkedQueue BFSDataQueue) {bool *isVisited = calloc(graph->vertexCount, sizeof(bool));LinkedQueue queue = linkedQueueConstructor();linkedQueueEnQueue(queue, graph->vertexList[getVertexIndex(graph, data) - 1]);BFS(graph, isVisited, queue, BFSDataQueue);for (int i = 1; i <= graph->vertexCount; ++i) {if (!isVisited[i - 1]) {BFS(graph, isVisited, queue, BFSDataQueue);}}
}
- 深度优先搜索(DFS):
- 从图的某一顶点出发,访问它的任一邻接顶点;再从邻接顶点出发,访问邻接顶点的任一邻接顶点;如此往复直到访问到一个所有邻接顶点都被访问的顶点为止;
- 接着回退一步,看看前一次访问的顶点是否还有其它没有被访问的邻接顶点;如果有,则访问此邻接顶点,之后再进行前述过程;如果没有,则再回退一步,重复上述过程,直到连通图中所顶点都被访问过为止。
void DFS(AdjacentListGraph graph, int vertexIndex, bool isVisited[], LinkedQueue DFSDataQueue) {Vertex vertex = graph->vertexList[vertexIndex - 1];linkedQueueEnQueue(DFSDataQueue, vertex->data);isVisited[vertexIndex - 1] = true;for (Vertex j = firstVertex(graph, vertex->data); j != NULL; j = nextVertex(graph, vertex->data, j->data)) {int index = getVertexIndex(graph, j->data);if (!isVisited[index - 1]) {DFS(graph, index, isVisited, DFSDataQueue);}}
}/*** 深度优先遍历* @param graph* @param data* @param DFSDataQueue*/
void DFSTraverse(AdjacentListGraph graph, void *data, LinkedQueue DFSDataQueue) {bool *isVisited = calloc(graph->vertexCount, sizeof(bool));int index = getVertexIndex(graph, data);DFS(graph, index, isVisited, DFSDataQueue);for (int i = 1; i <= graph->vertexCount; ++i) {if (!isVisited[i - 1]) {DFS(graph, i, isVisited, DFSDataQueue);}}
}
最小生成树
对于一个带权连通无向图 G G G,生成树不同,每棵树的权值也可能不同,若 T T T为权值最小的生成树,则 T T T称为 G G G的最小生成树(MST)。最小生成树的性质如下:
- 如果 G G G中有权值相等的边,则最小生成树不是唯一的,若 G G G的边数比顶点数少一,则 G G G的生成树就是它本身。
- 最小生成树的边的权值是唯一的,且是最小的。
- 最小生成树的边数为顶点数减一。
- U U U是V的一个子集,若 ( u , v ) (u,v) (u,v)是一条具有最小权值的边,其中 u ∈ U , v ∈ V − U u∈U,v∈V-U u∈U,v∈V−U,则必存在一棵包含 ( u , v ) (u,v) (u,v)的最小生成树。
普里姆算法(Prim)
普里姆算法的步骤:
- 初始时从图中选择一个顶点加入树 T T T,此时树中只有这一个顶点;
- 之后选择一个与当前 T T T中顶点集合距离最近的顶点,并将该顶点和相应的边加入 T T T;
- 以此类推,直到图中所有的顶点都加入 T T T,得到的 T T T就是最小生成树。
/*** Prim算法* @param graph* @return*/
AdjacentListGraph Prim(AdjacentListGraph graph) {AdjacentListGraph MST = adjacentListGraphConstructor(graph->vertexCount, graph->compare);//是否加入最小生成树bool isJoin[graph->vertexCount];//路径长度int distance[graph->vertexCount];//路径前驱int path[graph->vertexCount];for (int i = 0; i < graph->vertexCount; ++i) {isJoin[i] = false;distance[i] = INFINITY;path[i] = -1;}while (MST->size != graph->vertexCount) {int fromIndex = -1, toIndex = -1, minDistance = 0;if (MST->vertexCount == 0) {toIndex = 1;} else {for (int i = 1; i <= graph->vertexCount; ++i) {if (isJoin[i - 1] == false && distance[i - 1] < minDistance) {fromIndex = path[i - 1];toIndex = i;minDistance = distance[i - 1];}}if (toIndex == -1) {break;}}isJoin[toIndex - 1] = true;distance[toIndex - 1] = minDistance;path[toIndex - 1] = fromIndex;for (Edge edge = graph->vertexList[toIndex - 1]->firstEdge; edge != NULL; edge = edge->next) {if (edge->weight < distance[edge->vertexIndex - 1]) {distance[edge->vertexIndex - 1] = edge->weight;path[edge->vertexIndex - 1] = toIndex;}}insertVertex(MST, graph->vertexList[toIndex - 1]->data);MST->vertexCount++;addEdge(MST, graph->vertexList[fromIndex - 1]->data, graph->vertexList[toIndex - 1]->data);MST->edgeCount++;fromIndex = -1;toIndex = -1;minDistance = 0;}return MST;
}
克鲁斯卡尔算法(Kruskal)
克鲁斯卡尔算法的步骤:
- 将所有顶点都加入树 T T T,但是不加入边信息;
- 然后在图中寻找权值最小的边,若该边依附的顶点落在树 T T T的顶点上,且不形成环,那么就把该边加入到树 T T T中,否则就舍弃该边;
- 依次类推,直至T中所有顶点都连通。
/*** 克鲁斯卡尔算法* @param graph * @return */
AdjacentListGraph Kruskal(AdjacentListGraph graph) {AdjacentListGraph MST = adjacentListGraphConstructor(graph->vertexCount, graph->compare);PriorityQueue queue = priorityQueueConstructor(graph->compare);DisjointSet set = disjointSetConstructor(graph->vertexCount, graph->compare);for (int i = 1; i <= graph->vertexCount; ++i) {Vertex vertex = graph->vertexList[i - 1];disjointSetInsert(set, vertex->data);insertVertex(MST, vertex->data);for (Edge edge = graph->vertexList[i - 1]->firstEdge; edge != NULL; edge = edge->next) {int *tuple = calloc(3, sizeof(int));tuple[0] = i;tuple[1] = edge->vertexIndex;tuple[2] = edge->weight;priorityQueueEnQueue(queue, tuple);}}while (!priorityQueueIsEmpty(queue)) {int *tuple = priorityQueueDeQueue(queue);Vertex fromVertex = graph->vertexList[tuple[0] - 1];Vertex toVertex = graph->vertexList[tuple[1] - 1];int weight = tuple[2];if (graph->compare(disjointSetFind(set, fromVertex->data), disjointSetFind(set, toVertex->data)) != 0) {addEdge(MST, fromVertex->data, toVertex->data);setWeight(MST, fromVertex->data, toVertex->data, weight);disjointSetUnion(set, fromVertex, toVertex);}}return MST;
}
最短路径
在图中,把一个顶点到另一个顶点的一条路径所经过边上的权值 (无权图视为权为 1 1 1)之和称为该路径的带权路径长度,带权路径长度最短的路径称为最短路径。两点之间的最短路径一定包含路径上其它顶点之间的最短路径。其中:
- 无权图的单源最短路径问题可由 B F S BFS BFS算法和 D i j k s t r a Dijkstra Dijkstra算法解决
- 带权图的单源最短路径问题可由 D i j k s t r a Dijkstra Dijkstra算法解决
- 带权图和无权图的各顶点最短路径问题可由 F l o y d Floyd Floyd算法解决
BFS求最短路径
/*** BFS求无权图最短路径* @param graph * @param startVertex * @param endVertex * @param stack */
void BFSMinPath(AdjacentListGraph graph, void *startVertex, void *endVertex, SequenceStack stack) {//起始顶点到各个顶点的最短路径int distance[graph->vertexCount];//最短路径从哪个顶点过来int path[graph->vertexCount];bool isVisited[graph->vertexCount];for (int i = 0; i < graph->vertexCount; ++i) {distance[i] = INFINITY;path[i] = -1;isVisited[i] = false;}int startIndex = getVertexIndex(graph, startVertex);LinkedQueue queue = linkedQueueConstructor();distance[startIndex - 1] = 0;isVisited[startIndex - 1] = true;linkedQueueEnQueue(queue, startVertex);while (linkedQueueIsEmpty(queue)) {Vertex vertex = linkedQueueDeQueue(queue);for (Vertex near = firstVertex(graph, vertex->data); near != NULL; near = nextVertex(graph, vertex->data, near->data)) {int nearIndex = getVertexIndex(graph, near->data);if (!isVisited[nearIndex - 1]) {distance[nearIndex - 1] = distance[startIndex - 1] + 1;path[nearIndex - 1] = startIndex;isVisited[nearIndex - 1] = true;linkedQueueEnQueue(queue, near);}}}int minPath = getVertexIndex(graph, endVertex);while (path[minPath - 1] != -1) {sequenceStackPush(stack, graph->vertexList[minPath - 1]);minPath = path[minPath - 1];}
}
迪杰斯特拉算法(Dijkstra)
算法思想:
- 首先找出源顶点到达其它顶点的直达路径,不能直达记为无穷大。
- 从这些路径中挑选一条长度最短的路径。并将该顶点加入集合S。
- 对其余的路径进行调整,若能经过找到的最短路径到达其它顶点并且该路径之和比直达路径小,那么就是用该路径替代原来的直达路径。并将该顶点加入集合S。
- 之后重复上述步骤直到所有顶点都加入到S集合。
缺陷:不适用于负权值带权图
/*** 迪杰斯特拉算法* @param graph* @param startVertex* @param endVertex* @param stack*/
void Dijkstra(AdjacentListGraph graph, void *startVertex, void *endVertex, SequenceStack stack) {int findCount = 0;//标记各顶点是否找到最短路径bool isFind[graph->vertexCount];//最短路径长度int distance[graph->vertexCount];//路径前驱int path[graph->vertexCount];for (int i = 0; i < graph->vertexCount; ++i) {isFind[i] = false;distance[i] = INFINITY;path[i] = -1;}while (findCount != graph->vertexCount) {int fromIndex = -1, toIndex = -1, minDistance = 0;if (findCount == 0) {toIndex = getVertexIndex(graph, startVertex);} else {for (int i = 1; i <= graph->vertexCount; ++i) {if (isFind[i - 1] == false && distance[i - 1] < minDistance) {fromIndex = path[i - 1];toIndex = i;minDistance = distance[i - 1];}}if (toIndex == -1) {break;}}isFind[toIndex - 1] = true;distance[toIndex - 1] = minDistance;path[toIndex - 1] = fromIndex;for (Edge edge = graph->vertexList[toIndex - 1]->firstEdge; edge != NULL; edge = edge->next) {if (distance[toIndex - 1] + edge->weight < distance[edge->vertexIndex - 1]) {distance[edge->vertexIndex - 1] = distance[toIndex - 1] + edge->weight;path[edge->vertexIndex - 1] = toIndex;}}findCount++;fromIndex = -1;toIndex = -1;minDistance = 0;}int minPath = getVertexIndex(graph, endVertex);while (path[minPath - 1] != -1) {sequenceStackPush(stack, graph->vertexList[minPath - 1]);minPath = path[minPath - 1];}
}
弗洛伊德算法(Floyd)
- 逐个顶点试探,选出一条路径长度最短的。
- 初始时用一个矩阵存储各个顶点之间的距离,如果存在直达路径则记录直达路径,否则记录为无穷大。
- 逐步在原直接路径中增加中间顶点,若加入中间顶点后路径变短,则修改矩阵中的值,否则矩阵中的值不变。
- 所有顶点试探完毕,算法结束。
有向无环图
若一个有向图中不存在环,则称该图为有向无环图,简称DAG图。若用DAG图表示一个工程的各个子工程及其相互制约的关系:
-
其中以顶点表示活动,弧表示活动之间的优先制约关系。则将这样的图称为AOV网。AOV网的特点如下:
- 若从A到B有一条有向路径,则A是B的前驱,B是A的后继。
- 若AB是网中的有向边,则A是B的直接前驱,B是A的直接后继。
-
其中以弧表示活动,顶点表示活动之的开始和结束事件。则将这样的图称为AOE网。AOE网的性质如下:
- 只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始。
- 只有在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发生。
AOV网的拓扑结构
在AOV网中,我们将全部活动排列成一个线性序列,使得若AOV网中有边AB存在,则在这个序列中,A一定排在B的前面,具有这种性质的线性序列称为拓扑有序序列。即做事的先后顺序。用于求解拓扑序列的算法称为拓扑排序算法,拓扑排序算法可以用于检测图中是否含有环:如果拓扑序列中含有所有图中的结点,那么该图就没有环,否则就含有环。
拓扑排序
拓扑排序的算法思想如下:
- 在AOV网中选一个没有前驱的顶点,然后从图网中删除该顶点以及以这个顶点为起点的边。
- 重复上面的步骤,直到网为空或网中不存在无前驱的顶点为止。
/*** 拓扑排序* @param graph* @param queue*/
void topologicalSort(AdjacentListGraph graph, LinkedQueue queue) {SequenceStack stack = sequenceStackConstructor(graph->vertexCount);int inDegreeList[graph->vertexCount];for (int i = 1; i <= graph->vertexCount; ++i) {inDegreeList[i - 1] = getInDegree(graph, graph->vertexList[i - 1]->data);if (inDegreeList[i - 1] == 0) {sequenceStackPush(stack, graph->vertexList[i - 1]);}}while (!sequenceStackIsEmpty(stack)) {Vertex vertex = sequenceStackPop(stack);linkedQueueEnQueue(queue, vertex->data);for (Edge edge = vertex->firstEdge; edge != NULL; edge = edge->next) {if (--inDegreeList[edge->vertexIndex - 1] == 0) {sequenceStackPush(stack, graph->vertexList[edge->vertexIndex - 1]);}}}
}
逆拓扑排序
逆拓扑排序的算法思想如下:
- 在AOV网中选一个没有后继的顶点,然后从图网中删除该顶点以及以这个顶点为终点的边。
- 重复上面的步骤,直到网为空或网中不存在无后继的顶点为止。
void DFS(AdjacentListGraph graph, int index, int isVisited[], LinkedQueue queue) {isVisited[index - 1] += 2;Vertex vertex = graph->vertexList[index - 1];for (Edge edge = vertex->firstEdge; edge != NULL; edge = edge->next) {if (isVisited[edge->vertexIndex - 1] == 0) {DFS(graph, edge->vertexIndex, isVisited, queue);}if (isVisited[edge->vertexIndex - 1] == 2) {throw Error(CYCLIC_GRAPH_ERROR, "图中含有环,逆拓扑排序失败");}}isVisited[index - 1]--;linkedQueueEnQueue(queue, vertex->data);
}/*** 深度优先算法求逆拓扑排序* @param graph* @param queue*/
void DFSInTopologicalSort(AdjacentListGraph graph, LinkedQueue queue) {int *isVisited = calloc(graph->vertexCount, sizeof(bool));for (int i = 1; i <= graph->vertexCount; ++i) {if (isVisited[i - 1] == 0) {DFS(graph, i, isVisited, queue);}}
}
AOE网的关键路径
在AOE网中,入度为零的顶点称为源点,出度为零的顶点称为汇点,关键路径是指从源点到汇点路径长度最长的路径。关键路径上的活动称为关键活动。完成整个工程最短的时间就是关键路径的长度。
相关文章:

数据结构和算法——用C语言实现所有图状结构及相关算法
文章目录 前言图的基本概念图的存储方式邻接矩阵邻接表十字链表临界多重表 图的遍历最小生成树普里姆算法(Prim)克鲁斯卡尔算法(Kruskal) 最短路径BFS求最短路径迪杰斯特拉算法(Dijkstra)弗洛伊德算法&…...

JavaScript一些数据类型介绍
JavaScript一些数据类型介绍 1)数字类型(Number):可以表示整数和浮点数,例如:42、3.14159。 var x 42; // x 的类型是 Number var y 3.14159; // y 的类型是 Number2)字符串类型(…...

正向代理和反向代理与负载均衡
自存用 什么是反向代理,反向代理与正向代理的区别 一文帮你梳理清楚「正向代理和反向代理的区别与联系」 什么是反向代理服务器 正向代理为用户服务,给用户换个ip使其能访问其他网站 反向代理为服务器服务,使用户访问特定网站服务器。反向代…...

制造执行系统(MES)的核心功能是什么?
“一般来讲,制造执行系统(MES)的功能模块包括过程监控,质量管理,设备监控,计划执行等功能模块。” 为了深入探讨MES的核心功能,本文将从以下3个方面展开说明: 首先,从概…...
uniapp如何使用mumu模拟器
模拟器安装 下载地址:MuMu模拟器 模拟器相关设置 1.在设置-显示中选中手机版,设置手机分辨率 2.设置-关于手机-版本号快速点击,将其设置为开发者模式 3.选择多开器 4.打开hbuilderx,找到adb设置 5.配置adb路径及端口号&#x…...
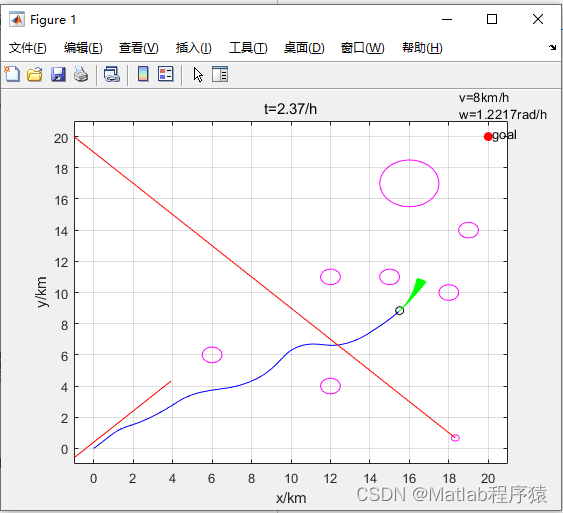
【MATLAB源码-第64期】matlab基于DWA算法的机器人局部路径规划包含动态障碍物和静态障碍物。
操作环境: MATLAB 2022a 1、算法描述 动态窗口法(Dynamic Window Approach,DWA)是一种局部路径规划算法,常用于移动机器人的导航和避障。这种方法能够考虑机器人的动态约束,帮助机器人在复杂环境中安全、…...
阿里云国际版和国内版的区别是什么,为什么很多人喜欢选择国际版?
阿里云国际版和国内版区别如下: 谈到区别,我们不妨先来对比下相同点与不同点,才能清晰明确的知道二者区别 下面先介绍不同点: 面向市场更广泛 阿里云国际版主要是面向国际(全球)客户的,而国内…...

监听redis过期业务处理
配置类: package com.testimport org.springframework.beans.factory.annotation.Autowired; import org.springframework.cache.annotation.CachingConfigurerSupport; import org.springframework.cache.annotation.EnableCaching; import org.springframework.c…...

计算机网络与技术——数据链路层
😊计算机网络与技术——数据链路层 🚀前言☃️基本概念🥏封装成帧🥏透明传输🥏差错检测 ☃️点对点协议PPP🥏PPP协议的特点🥏PPP协议的帧格式🔍PPP异步传输时透明传输(字…...
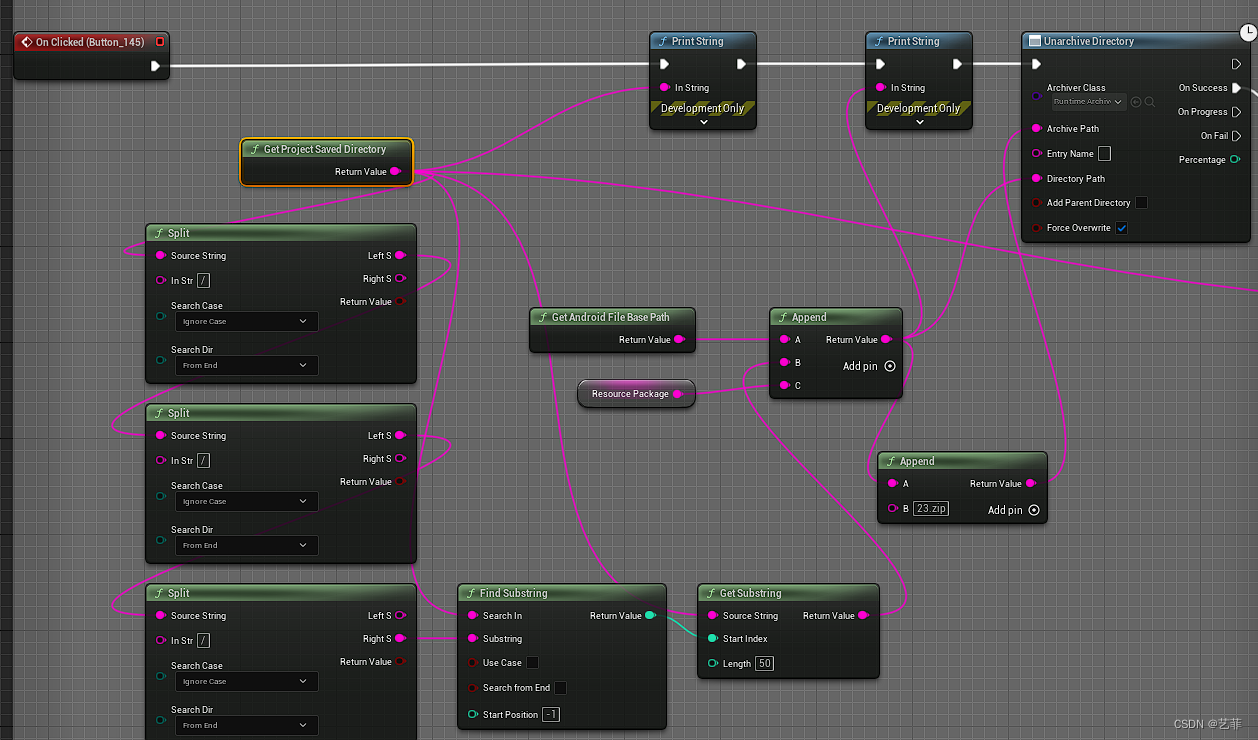
UE5 Android下载zip文件并解压缩到指定位置
一、下载是使用市场的免费插件 二、解压缩是使用市场的免费插件 三、Android路径问题 windows平台下使用该插件没有问题,只是在Android平台下,只有使用绝对路径才能进行解压缩,所以如何获得Android下的绝对路径?增加C文件获得And…...
CSS3盒模型
CSS3盒模型规定了网页元素的显示方式,包括大小、边框、边界和补白等概念。2015年4月,W3C的CSS工作组发布了CSS3基本用户接口模块,该模块负责控制与用户接口界面相关效果的呈现方式。 1、盒模型基础 在网页设计中,经常会听到内容…...
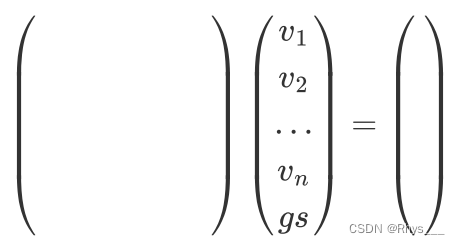
VINS-Mono-VIO初始化 (五:视觉惯性对齐求解)
整体思想就是根据预积分的公式,把已知量和未知量各放到一边,因为前面的数据都是变换到 c 0 c_{0} c0下的,不是真正意义上和重力对齐的世界坐标,然后位移和速度的预积分中会用到加速度计获取的重力加速度g,但是这个重…...

详解Vue——的双向数据绑定是如何实现的?
引言 在现代的Web开发中,数据绑定是一个非常重要的概念。Vue.js是一种流行的JavaScript框架,它提供了一种简单而强大的方式来实现双向数据绑定。本文将介绍Vue的双向数据绑定原理,并提供相关代码示例。 什么是双向数据绑定? 双向…...
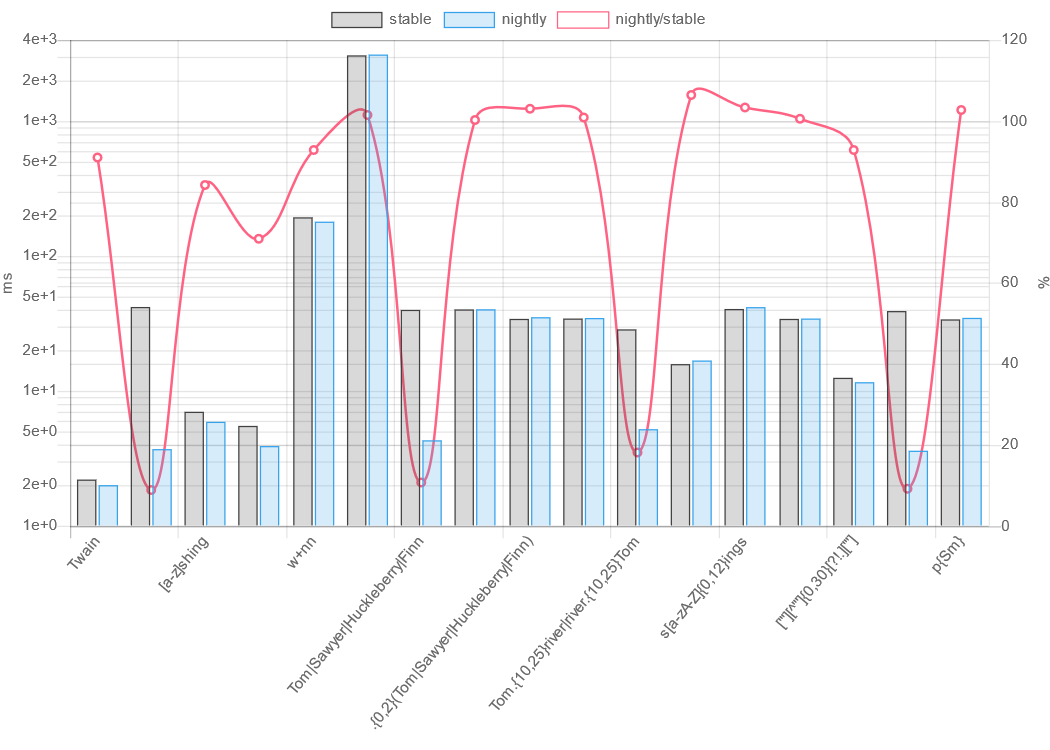
正则表达式引擎比较(翻译自:A comparison of regex engines)
原文: A comparison of regex engines – Rust Leipzig 引言 正则表达式(或简称regex)通常用于模式搜索算法。 有许多不同的正则表达式引擎提供不同的表达式支持、性能约束和语言绑定。 基于 John Maddock 之前的工作 (regex comparison)和…...

后端Linux软件安装大全[JDK、Tomcat、MySQL、Irzsz、Git、Maven、Redis、Nginx...持续更新中]
文章目录 前言1.软件安装方式2.安装jdk3.安装Tomcat4.安装MySQL5.安装lrzsz6. 安装Git7. 安装Maven8. 安装Redis9. 安装Nginx 总结 前言 为了巩固所学的知识,作者尝试着开始发布一些学习笔记类的博客,方便日后回顾。当然,如果能帮到一些萌新…...

C++ Dijkstra 最短路径求解算法的两种实现方案
迪杰斯特拉算法(Diikstra) 是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。 核心思想,搜索到某一个顶点后,更新与其相邻顶点的权重。顶点权重的数据含义表示从起始点到此点的最短路径长度(也就是经过的…...

因存在色情内容,夸克被罚50万元
媒体经济的繁荣、自媒体、直播等各种形式的信息传播疯狂发展,但是各种形式的信息资源大规模生产时,“色情”,“暴力”的图像和视频不可控的滋生,特别是某些 APP 或浏览器。一旦打开,满屏都是“哥哥,快来啊”…...
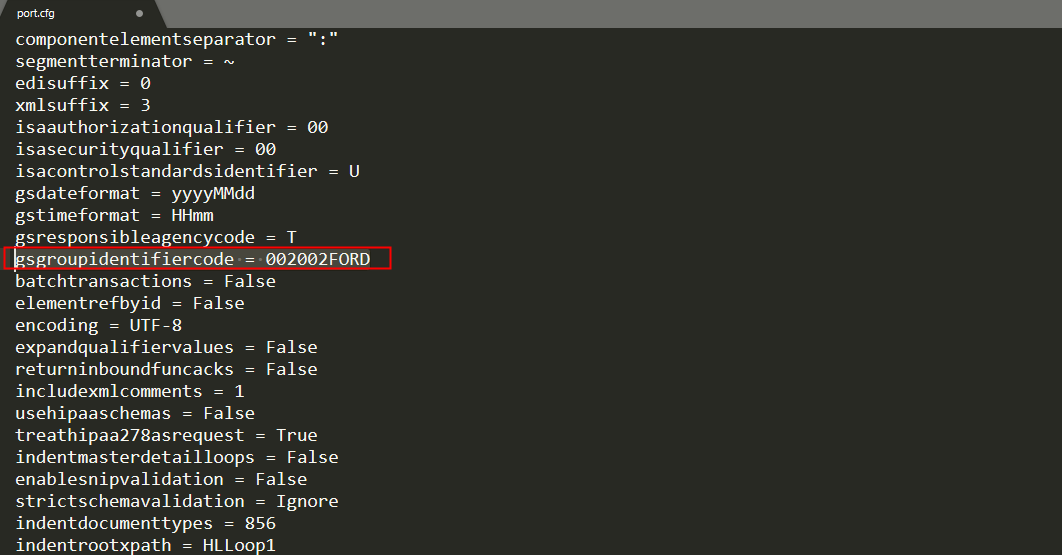
汽车EDI:福特Ford EDI项目案例
项目背景 福特(Ford)是世界著名的汽车品牌,为美国福特汽车公司(Ford Motor Company)旗下的众多品牌之一。此前的文章福特FORD EDI需求分析中,我们已经了解了福特Ford EDI 的大致需求,本文将会介…...

正则表达式的使用实例
正则表达式的使用实例 1- 表示2- 实例 1- 表示 1, [:digit:] 表示0-9全部十个数字 //等价于 0123456789, 而不等价于[0123456789] 2, [[:digit:]] 表示任意一个数字 \{m,n\} 表示其前面的字符出现最少m次,最多n次的情况 \{3,\} 其前面的字符出…...
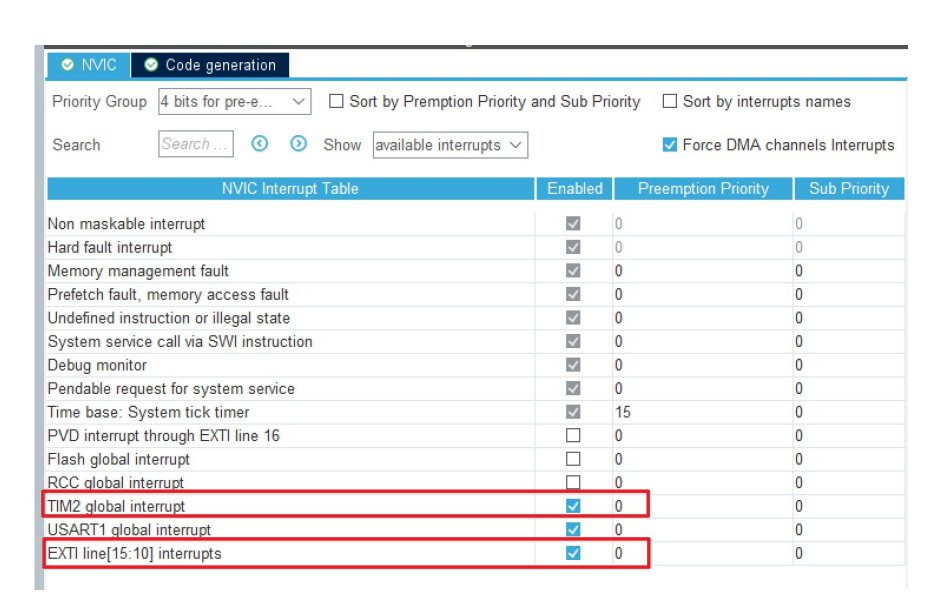
STM智能小车——OLED实现测速小车
目录 1. 测速模块 2. 测试原理和单位换算 3. 定时器和中断实现测速开发和调试代码 4. 小车速度显示在OLED屏 1. 测速模块 用途:广泛用于电机转速检测,脉冲计数,位置限位等。有遮挡,输出高电平;无遮挡,输出低电平接线…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
