VINS-Mono-VIO初始化 (五:视觉惯性对齐求解)
整体思想就是根据预积分的公式,把已知量和未知量各放到一边,因为前面的数据都是变换到 c 0 c_{0} c0下的,不是真正意义上和重力对齐的世界坐标,然后位移和速度的预积分中会用到加速度计获取的重力加速度g,但是这个重力g是没有和世界的重力方向对齐的,所以里面就存在了未知量,通过每组预积分的数据联立起来构成一个大矩阵对重力向量进行求解,这里是求解了重力方向(对于起始帧 c 0 c_{0} c0的重力方向),重力大小也有,不过不准确,所以后续还会利用重力先验对方向进行调整
有个小问题:这个预积分前面不是也会涉及重力吗,是直接不理会当作影响不大来进行处理?那这个已知量里面也包含里一定的未知量的积分影响在里面,待我看下代码确定一下整体的初始化流程和思想,后续会出篇整体初始化思想流程
关于位移的预积分量的定义,把 c 0 c_{0} c0 换成 w w w 就是之前的式子了,因为重力还没对齐所以只转换到 c 0 c_{0} c0 坐标系下,就是系统开始的第一帧下
先对平移进行推导

上一节零偏估计里面推导出这个式子

代入进去则有
R c 0 b k ( s P c k + 1 c 0 − R b k + 1 c 0 ⋅ P c b ) = R c 0 b k [ s P c k c 0 − R b k c 0 ⋅ P c b + R c 0 b k ⋅ v b k ⋅ Δ t − 1 2 g c 0 Δ t 2 + α ] R^{b_{k}}_{c_{0}}(sP^{c_{0}}_{c_{k+1}}-R^{c_{0}}_{b_{k+1}}·P^{b}_{c})=R^{b_{k}}_{c_{0}}[sP^{c_{0}}_{c_{k}}-R^{c_{0}}_{b_{k}}·P^{b}_{c}+R^{b_{k}}_{c_{0}}·v^{b_{k}}·Δt-\frac{1}{2}g^{c_{0}}Δt^{2}+α] Rc0bk(sPck+1c0−Rbk+1c0⋅Pcb)=Rc0bk[sPckc0−Rbkc0⋅Pcb+Rc0bk⋅vbk⋅Δt−21gc0Δt2+α]
原本的 v b k c 0 v^{c_{0}}_{b_{k}} vbkc0 指的是再 c 0 c_{0} c0 坐标系下 b k b_{k} bk 的速度,现在直接拿在 b k b_{k} bk 系下的速度通过旋转矩阵进行变换,其实意思是一样的。
现在把已知量放左边,未知量放右边
α − P c b ⋅ R c 0 b k ⋅ R b k + 1 c 0 ⋅ P c b = R c 0 b k ( P c k + 1 c 0 − P c k c 0 ) s − v b k Δ t + 1 2 R c 0 b k g c 0 Δ t 2 α-P^{b}_{c}·R^{b_{k}}_{c_{0}}·R^{c_{0}}_{b_{k+1}}·P^{b}_{c}=R^{b_{k}}_{c_{0}}(P^{c_{0}}_{c_{k+1}}-P^{c_{0}}_{c_{k}})s-v^{b_{k}}Δt+\frac{1}{2}R^{b_{k}}_{c_{0}}g^{c_{0}}Δt^{2} α−Pcb⋅Rc0bk⋅Rbk+1c0⋅Pcb=Rc0bk(Pck+1c0−Pckc0)s−vbkΔt+21Rc0bkgc0Δt2
左边都是已知量,最后是一个 3 × 1 3×1 3×1 的一个向量
上面的式子就和论文中的公式对应了


对速度进行推导
根据原始预积分的定义有
R c 0 b k ⋅ V b k + 1 c 0 = R c 0 b k ( V b k c 0 − g c 0 ⋅ Δ t ) + β R^{b_{k}}_{c_{0}}·V^{c_{0}}_{b_{k+1}}=R^{b_{k}}_{c_{0}}(V^{c_{0}}_{b_{k}}-g^{c_{0}}·Δt)+β Rc0bk⋅Vbk+1c0=Rc0bk(Vbkc0−gc0⋅Δt)+β
然后变换一下表达方式,含义是不变的
= > R c 0 b k ⋅ R b k + 1 c 0 ⋅ V b k + 1 = R c 0 b k ( R b k c 0 ⋅ V b k − g c 0 ⋅ Δ t ) + β =>R^{b_{k}}_{c_{0}}·R^{c_{0}}_{b_{k+1}}·V^{b_{k+1}}=R^{b_{k}}_{c_{0}}(R^{c_{0}}_{b_{k}}·V^{b_{k}}-g^{c_{0}}·Δt)+β =>Rc0bk⋅Rbk+1c0⋅Vbk+1=Rc0bk(Rbkc0⋅Vbk−gc0⋅Δt)+β
同样把已知量放左边,未知量放右边
= > β = − V b k + R c 0 b k ⋅ R b k + 1 c 0 ⋅ V b k + 1 + R c 0 b k ⋅ g c 0 ⋅ Δ t =>β=-V^{b_{k}}+R^{b_{k}}_{c_{0}}·R^{c_{0}}_{b_{k+1}}·V^{b_{k+1}}+R^{b_{k}}_{c_{0}}·g^{c_{0}}·Δt =>β=−Vbk+Rc0bk⋅Rbk+1c0⋅Vbk+1+Rc0bk⋅gc0⋅Δt
第 k 到 k+1 都会产生上面两个式子,会有很多个这种式子拼起来
构成 H x = b Hx=b Hx=b 的矩阵方程,代码中就是一些矩阵拼接的操作
x = [ v k , v k + 1 , g , s ] ∈ 10 × 1 x=[v_{k},v_{k+1},g,s]∈10×1 x=[vk,vk+1,g,s]∈10×1,所以 H 属于 10 × 10 H属于10×10 H属于10×10 , b ∈ 10 × 1 b∈10×1 b∈10×1,实际上由于有多组数据,10 会变成 N,速度,重力都是3维的,尺度因子是1,所以每一组就是 10
有多个数据则矩阵写为,通过对每一组数据进行矩阵分块填入这个大矩阵里面,然后一次性求解出所有速度、重力和尺度
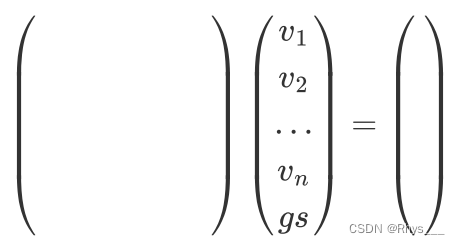
求解后获得重力向量
然后根据当地的重力先验来对刚才算出来的重力进行修正
相关文章:

VINS-Mono-VIO初始化 (五:视觉惯性对齐求解)
整体思想就是根据预积分的公式,把已知量和未知量各放到一边,因为前面的数据都是变换到 c 0 c_{0} c0下的,不是真正意义上和重力对齐的世界坐标,然后位移和速度的预积分中会用到加速度计获取的重力加速度g,但是这个重…...

详解Vue——的双向数据绑定是如何实现的?
引言 在现代的Web开发中,数据绑定是一个非常重要的概念。Vue.js是一种流行的JavaScript框架,它提供了一种简单而强大的方式来实现双向数据绑定。本文将介绍Vue的双向数据绑定原理,并提供相关代码示例。 什么是双向数据绑定? 双向…...
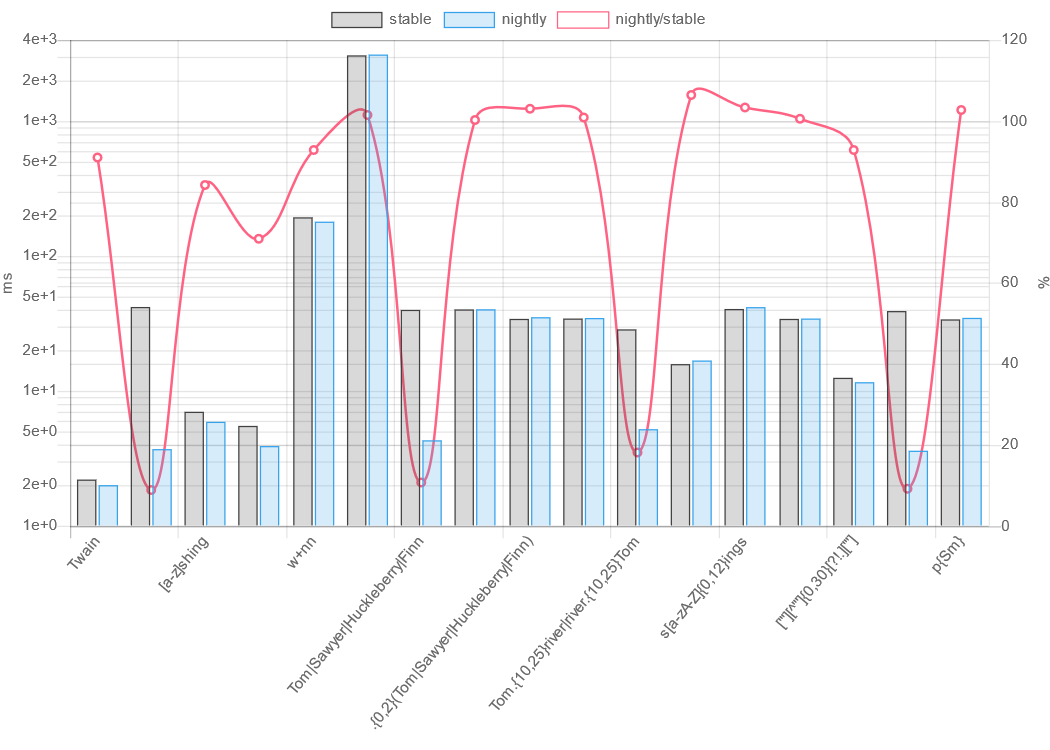
正则表达式引擎比较(翻译自:A comparison of regex engines)
原文: A comparison of regex engines – Rust Leipzig 引言 正则表达式(或简称regex)通常用于模式搜索算法。 有许多不同的正则表达式引擎提供不同的表达式支持、性能约束和语言绑定。 基于 John Maddock 之前的工作 (regex comparison)和…...

后端Linux软件安装大全[JDK、Tomcat、MySQL、Irzsz、Git、Maven、Redis、Nginx...持续更新中]
文章目录 前言1.软件安装方式2.安装jdk3.安装Tomcat4.安装MySQL5.安装lrzsz6. 安装Git7. 安装Maven8. 安装Redis9. 安装Nginx 总结 前言 为了巩固所学的知识,作者尝试着开始发布一些学习笔记类的博客,方便日后回顾。当然,如果能帮到一些萌新…...

C++ Dijkstra 最短路径求解算法的两种实现方案
迪杰斯特拉算法(Diikstra) 是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。 核心思想,搜索到某一个顶点后,更新与其相邻顶点的权重。顶点权重的数据含义表示从起始点到此点的最短路径长度(也就是经过的…...

因存在色情内容,夸克被罚50万元
媒体经济的繁荣、自媒体、直播等各种形式的信息传播疯狂发展,但是各种形式的信息资源大规模生产时,“色情”,“暴力”的图像和视频不可控的滋生,特别是某些 APP 或浏览器。一旦打开,满屏都是“哥哥,快来啊”…...
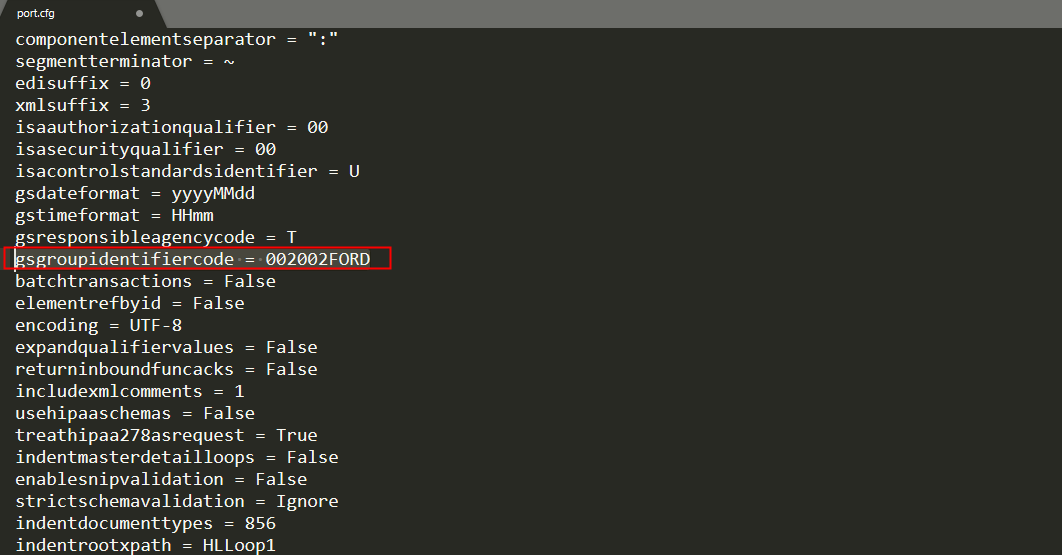
汽车EDI:福特Ford EDI项目案例
项目背景 福特(Ford)是世界著名的汽车品牌,为美国福特汽车公司(Ford Motor Company)旗下的众多品牌之一。此前的文章福特FORD EDI需求分析中,我们已经了解了福特Ford EDI 的大致需求,本文将会介…...

正则表达式的使用实例
正则表达式的使用实例 1- 表示2- 实例 1- 表示 1, [:digit:] 表示0-9全部十个数字 //等价于 0123456789, 而不等价于[0123456789] 2, [[:digit:]] 表示任意一个数字 \{m,n\} 表示其前面的字符出现最少m次,最多n次的情况 \{3,\} 其前面的字符出…...
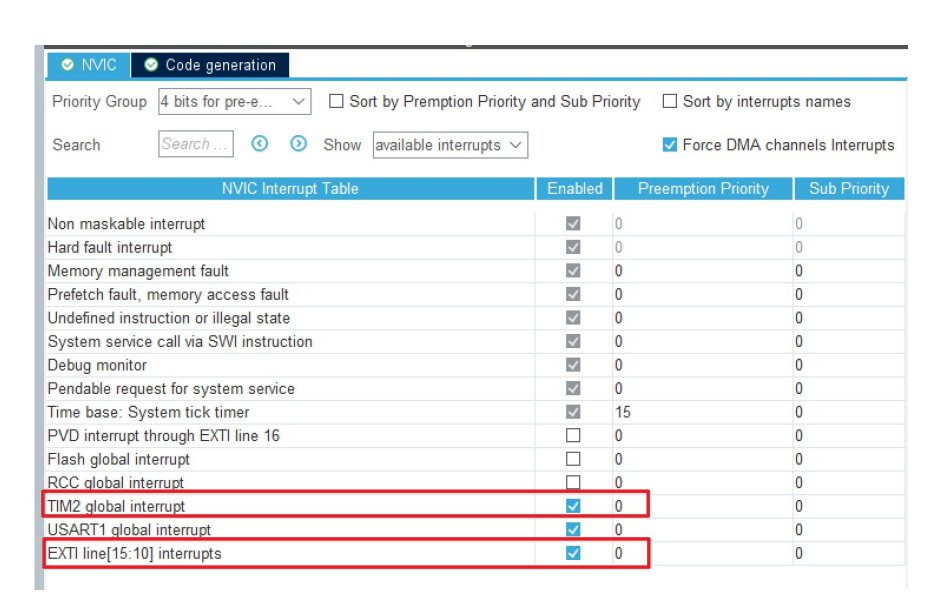
STM智能小车——OLED实现测速小车
目录 1. 测速模块 2. 测试原理和单位换算 3. 定时器和中断实现测速开发和调试代码 4. 小车速度显示在OLED屏 1. 测速模块 用途:广泛用于电机转速检测,脉冲计数,位置限位等。有遮挡,输出高电平;无遮挡,输出低电平接线…...

pod基本概念
目录 pod基本概念 pause容器 Pod分类: Pod容器的分类 1、基础容器(infrastructure container) 2、初始化容器(initcontainers) 3、应用容器(Maincontainer) 镜像拉取策略(im…...

SQL Server 中定时调度调用存储过程
要在SQL中定时调度调用存储过程,你可以使用SQL Server代理(如果你正在使用SQL Server数据库)。下面是一些步骤来配置SQL Server代理以定时调度调用存储过程: 打开SQL Server Management Studio (SSMS) 并连接到你的SQL Server实例…...

SpringCloud(三) Ribbon负载均衡
SpringCloud(二) Eureka注册中心的使用-CSDN博客 在SpringCloud(二)中学习了如何通过Eureka实现服务的注册和发送,从而通过RestTemplate实现不同微服务之间的调用,加上LoadBalance注解之后实现负载均衡,那负载均衡的原理是什么呢? 目录 一, 负载均衡 1.1 负载均衡原理 1.2 源…...

vue2:路由前置守卫无法获取到this.$store.state.xxx
在获取到vuex的数据时候,想在router目录下的index.js文件去获取到vuex仓库中声明的全局变量,但是通过this.$store.stote.xxx去获取的时候,报错提示:$store未定义 一、store/index.js const store new Vuex.Store({state: {// 属…...

Unity的碰撞检测(五)
温馨提示:本文基于前一篇“Unity的碰撞检测(四)”继续探讨两个游戏对象具备刚体的BodyType均为Dynamic,但是Collision Detection属性不同的碰撞检测,阅读本文则默认已阅读前文。 (一)测试说明 在基于两…...
管理)
Flutter笔记:Flutter的应用生命周期状态(lifecycleState)管理
Flutter笔记 Flutter的应用生命周期状态(lifecycleState)管理 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/…...
)
代碼隨想錄算法訓練營|第五十四天|300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组。刷题心得(c++)
讀題 300.最长递增子序列 看完代码随想录之后的想法 思想上很簡單,dp[i]表示i之前的包括i的numbers[i]節尾的最長上升子序列的長度 並且透過兩層迴圈,一層遍歷全部,一層遍歷到i,透過比較當前dp[i]還是dp[j] 1哪個比較大&…...

正点原子嵌入式linux驱动开发——Linux 串口RS232/485/GPS 驱动
串口是很常用的一个外设,在Linux下通常通过串口和其他设备或传感器进行通信,根据 电平的不同,串口分为TTL和RS232。不管是什么样的接口电平,其驱动程序都是一样的,通过外接RS485这样的芯片就可以将串口转换为RS485信号…...
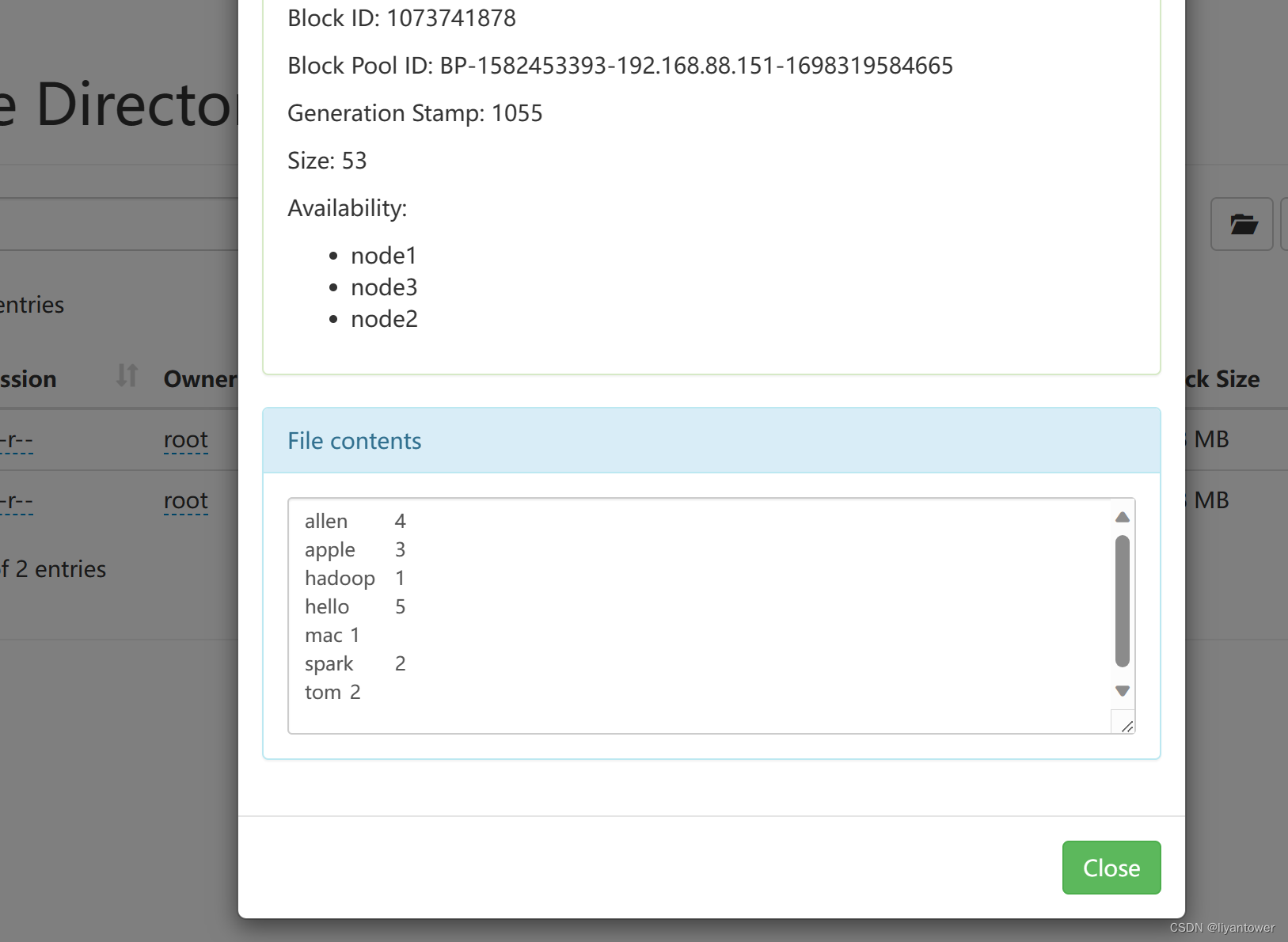
HDFS工作流程和机制
HDFS写数据流程(上传文件) 核心概念--Pipeline管道 HDFS在上传文件写数据过程中采用的一种传输方式。 线性传输:客户端将数据写入第一个数据节点,第一个数据节点保存数据之后再将快复制到第二个节点,第二节点复制给…...

CMMI/ASPICE认证咨询及工具服务
服务概述 质量专家戴明博士的名言“如果你不能描述做事情的过程,那么你不知道你在做什么”。过程是连接有能力的工程师和先进技术的纽带,因此产品开发过程直接决定了产品的质量和研发的效率。 经纬恒润可结合多体系要求,如IATF16949\ISO26262…...
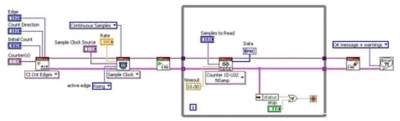
【NI-DAQmx入门】计数器
1.计数器的作用 NI产品的计数器一般来说兼容TTL信号,定义如下:0-0.8V为逻辑低电平,2~5V为高电平,0.8-2V为高阻态,最大上升下降时间为50ns。 计数器可以感测上升沿(从逻辑低到逻辑高的转变)和下降…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...
