当前位置： 首页 > news >正文

CMMI/ASPICE认证咨询及工具服务

news 2025/8/27 16:00:22

服务概述
质量专家戴明博士的名言“如果你不能描述做事情的过程，那么你不知道你在做什么”。过程是连接有能力的工程师和先进技术的纽带，因此产品开发过程直接决定了产品的质量和研发的效率。
经纬恒润可结合多体系要求，如IATF16949\ISO26262\ISO21434等，梳理业务流程、进行过程定义、与CMMI和ASPICE标准对标、进行差距分析、给出改进建议，建立“可视化”的过程。同时，我们结合IBM的ELM \PTC的CodeBeamer\Method Park by UL 的Stages过程管理工具将已定义的企业过程在平台中固化。

在这里插入图片描述

业务范围

  • 培训：ASPICE标准培训、助理评估师培训、满足ASPICE要求的需求工程、架构设计/建模、测试技能培训
  • ASPICE咨询：满足功能安全/网络安全的ASPICE流程搭建及试运行指导
  • ASPICE评估：潜在供应商审核及ASPICE过程能力评估

在这里插入图片描述

经纬恒润ASPICE咨询优势

在这里插入图片描述

应用案例
经纬恒润已帮助多家主机厂、供应商基于ASPICE的要求进行过程改进并通过评估。也帮助某客户基于CMMI3级要求，改进控制系统软件研制过程，实现了客户的软件研制过程符合CMMI和DO-178C的要求，同时提高了控制系统软件研制的效率和质量。

在这里插入图片描述

相关文章：

CMMI/ASPICE认证咨询及工具服务

服务概述 质量专家戴明博士的名言“如果你不能描述做事情的过程，那么你不知道你在做什么”。过程是连接有能力的工程师和先进技术的纽带，因此产品开发过程直接决定了产品的质量和研发的效率。 经纬恒润可结合多体系要求，如IATF16949\ISO26262…...

编程日记 2023/11/1 7:48:16

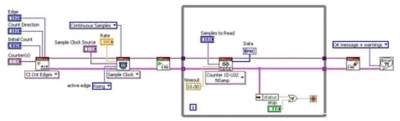
【NI-DAQmx入门】计数器

1.计数器的作用 NI产品的计数器一般来说兼容TTL信号，定义如下：0-0.8V为逻辑低电平，2~5V为高电平，0.8-2V为高阻态，最大上升下降时间为50ns。 计数器可以感测上升沿（从逻辑低到逻辑高的转变）和下降…...

编程日记 2023/11/1 7:47:15

Python爬取读书网的图片链接和书名并保存在数据库中

一个比较基础且常见的爬虫，写下来用于记录和巩固相关知识。 一、前置条件 本项目采用scrapy框架进行爬取，需要提前安装 pip install scrapy# 国内镜像 pip install scrapy -i https://pypi.douban.com/simple 由于需要保存数据到数据库，因…...

编程日记 2023/11/1 7:46:15

js解决加油站

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。 给定两个整数数组 gas 和 cost &…...

编程日记 2023/11/1 7:45:14

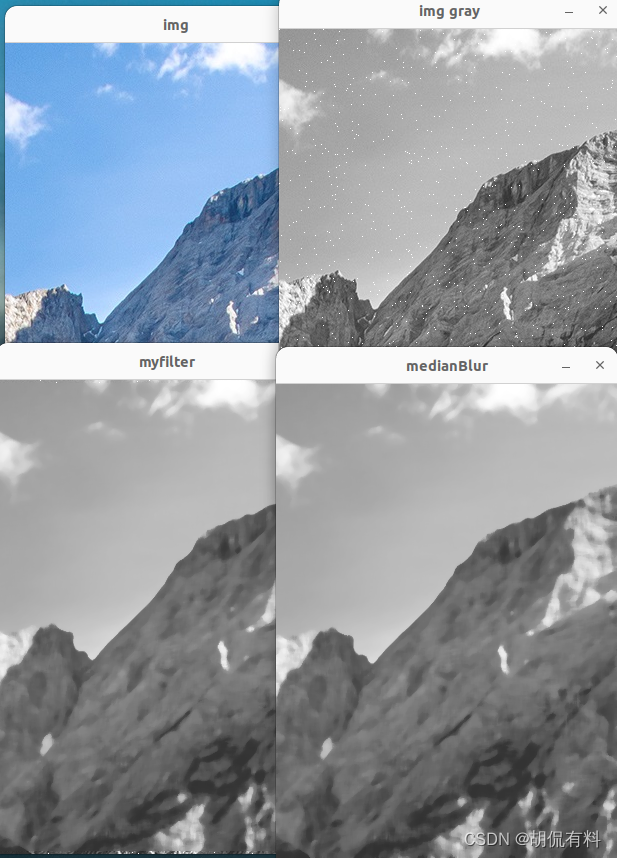
【c++|opencv】二、灰度变换和空间滤波---5.中值滤波

every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 1. 中值滤波 #include<iostream> #include<opencv2/opencv.hpp> #include"Salt.h"using namespace cv; using namespace std;voi…...

编程日记 2023/11/1 7:44:13

python之pytorch多进程

目录 1、创建并运行并行进程 2、使用队列&#xff08;Queue&#xff09;来共享数据 3、进程池 4、进程锁 5、比较使用多进程和使用单进程执行一段代码的时间消耗 6、共享变量 多进程是计算机科学中的一个术语&#xff0c;它是指同时运行多个进程&#xff0c;这些进程可以…...

编程日记 2023/11/1 7:43:12

sqoop 抽数报错com.mysql.cj.exceptions.WrongArgumentException: HOUR_OF_DAY: 2 -＞ 3

文章目录 1.sqoop 抽数报错: Caused by: com.mysql.cj.exceptions.WrongArgumentException: HOUR_OF_DAY: 2 -> 3 at sun.reflect.NativeConstructorAccessorImpl.newInstance0(Native Method) at sun.reflect.NativeConstructorAccessorImpl.newInstance(NativeConstructor…...

编程日记 2023/11/1 7:42:11

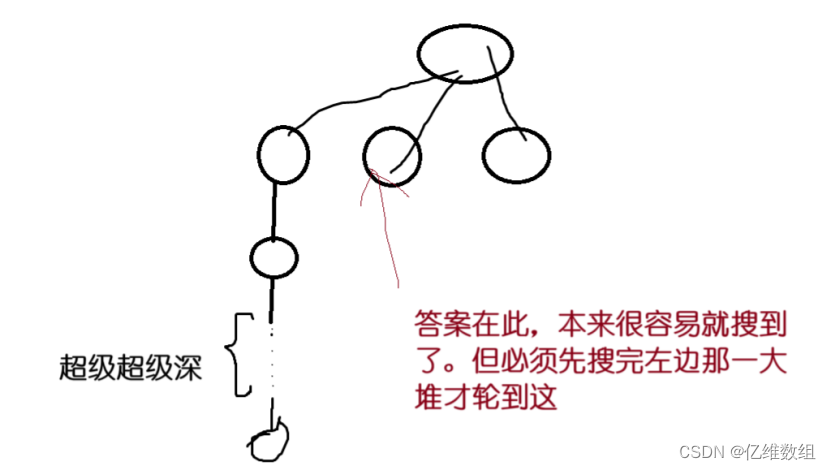
【Acwing170】加成序列（dfs+迭代加深+剪枝）题解和一点感想

本思路来自acwing算法提高课 题目描述 看本文需要准备的知识 1.dfs算法基本思想 2.对剪枝这个词有个简单的认识 迭代加深思想和此题分析 首先&#xff0c;什么是迭代加深呢&#xff1f;当一个问题的解有很大概率出现在递归树很浅的层&#xff0c;但是这个问题的解本身存在…...

编程日记 2023/11/1 7:41:10

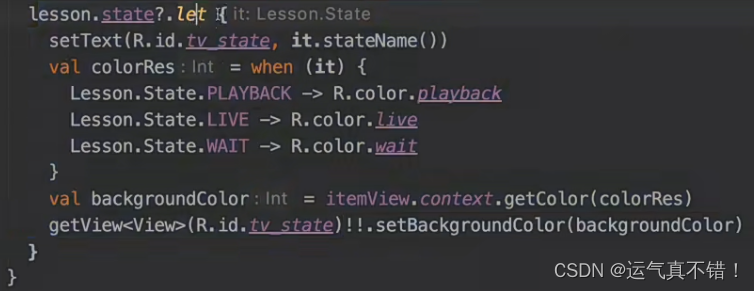
Android开发知识学习——Kotlin进阶

文章目录 次级构造主构造器init 代码块构造属性data class相等性解构Elvis 操作符when 操作符operatorLambdainfix 函数嵌套函数注解使用处目标函数简化函数参数默认值扩展函数类型内联函数部分禁用用内联具体化的类型参数抽象属性委托属性委托类委托 Kotlin 标准函数课后题 次…...

编程日记 2023/11/1 7:40:09

iOS使用AVCaptureSession实现音视频采集

AVCaptureSession配置采集行为并协调从输入设备到采集输出的数据流。要执行实时音视频采集&#xff0c;需要实例化采集会话并添加适当的输入和输出。 AVCaptureSession&#xff1a;管理输入输出音视频流AVCaptureDevice&#xff1a;相机硬件的接口&#xff0c;用于控制硬件特性…...

编程日记 2023/11/1 7:39:07

springboot和flask整合nacos，使用openfeign实现服务调用，使用gateway实现网关的搭建（附带jwt续约的实现）

环境准备&#xff1a; 插件版本jdk21springboot 3.0.11 springcloud 2022.0.4 springcloudalibaba 2022.0.0.0 nacos2.2.3&#xff08;稳定版&#xff09;python3.8 nacos部署&#xff08;docker&#xff09; 先创建目录&#xff0c;分别创建config&#xff0c;logs&#xf…...

编程日记 2023/11/1 7:38:06

深入浅出排序算法之基数排序

目录 1. 前言 1.1 什么是基数排序⭐⭐⭐ 1.2 执行流程⭐⭐⭐⭐⭐ 2. 代码实现⭐⭐⭐ 3. 性能分析⭐⭐ 3.1 时间复杂度 3.2 空间复杂度 1. 前言 一个算法&#xff0c;只有理解算法的思路才是真正地认识该算法&#xff0c;不能单纯记住某个算法的实现代码&#xff01; 1.…...

编程日记 2023/11/1 7:37:04

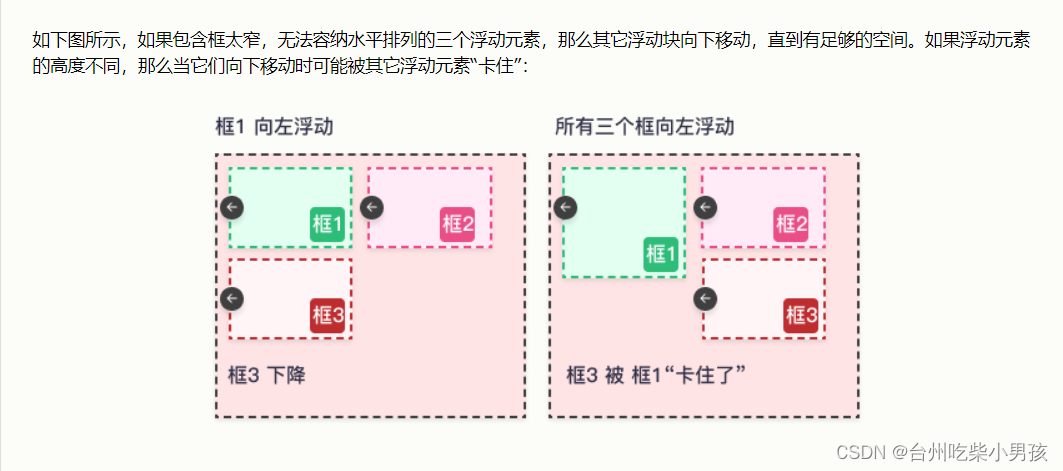
CSS选择器、CSS属性相关

CSS选择器 CSS属性选择器 通过标签的属性来查找标签&#xff0c;标签都有属性 <div class"c1" id"d1"></div>id值和class值是每个标签都自带的属性&#xff0c;还有另外一种&#xff1a;自定义属性 <div class"c1" id"d1&…...

编程日记 2023/11/1 7:36:03

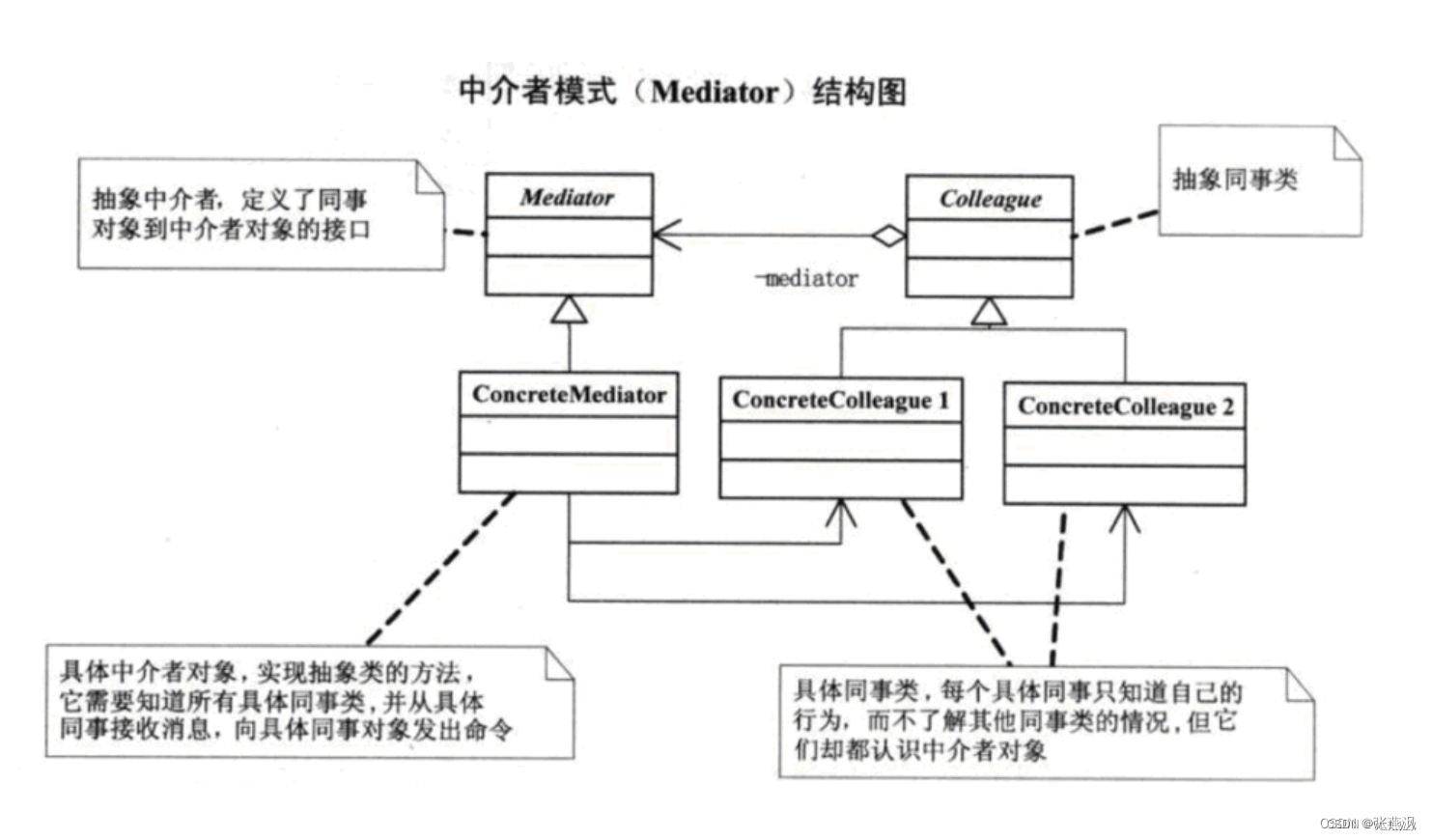
设计模式（21）中介者模式

一、介绍&#xff1a; 1、定义&#xff1a;中介者模式&#xff08;Mediator Pattern&#xff09;是一种行为型设计模式&#xff0c;它通过引入一个中介者对象来降低多个对象之间的耦合度。在中介者模式中&#xff0c;各个对象之间不直接进行通信&#xff0c;而是通过中介者对象…...

编程日记 2023/11/1 7:35:02

JVM虚拟机：通过一个例子解释JVM中栈结构的使用

代码 代码解析 main方法执行&#xff0c;创建栈帧并压栈。 int d8&#xff0c;d为局部变量&#xff0c;是基础类型&#xff0c;它位于虚拟机栈的局部变量表中 然后创建了一个TestDemo的对象&#xff0c;这个对象在堆中&#xff0c;并且这个对象的成员变量&#xff08;day&am…...

编程日记 2023/11/1 7:34:01

会自动写代码的AI大模型来了！阿里云推出智能编码助手通义灵码

用大模型写代码是什么样的体验&#xff1f;10月31日&#xff0c;杭州云栖大会上&#xff0c;阿里云对外展示了一款可自动编写代码的 AI 助手&#xff0c;在编码软件的对话窗口输入“帮我用 python 写一个飞机游戏”&#xff0c;短短几秒&#xff0c;这款名为“通义灵码”的 AI …...

编程日记 2023/11/1 7:33:00

如何公网远程访问本地WebSocket服务端

本地websocket服务端暴露至公网访问【cpolar内网穿透】 文章目录 本地websocket服务端暴露至公网访问【cpolar内网穿透】1. Java 服务端demo环境2. 在pom文件引入第三包封装的netty框架maven坐标3. 创建服务端,以接口模式调用,方便外部调用4. 启动服务,出现以下信息表示启动成功…...

编程日记 2023/11/1 7:31:58

python 练习 在列表元素中合适的位置插入 输入值

目的&#xff1a; 有一列从小到大排好的数字元素列表&#xff0c; 现在想往其插入一个值&#xff0c;要求&#xff1a; 大于右边数字小于左边数字 列表元素&#xff1a; [1,4,6,13,16,19,28,40,100] # 方法&#xff1a; 往列表中添加一个数值&#xff0c;其目的方便元素位置往后…...

编程日记 2023/11/1 7:30:58

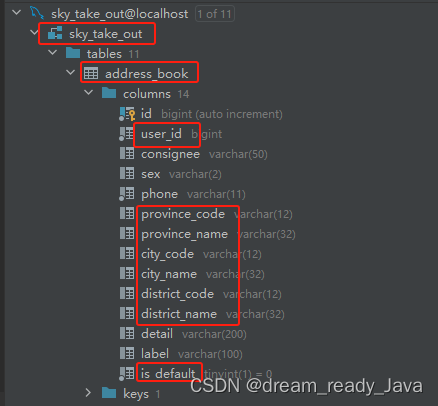
企业级JAVA、数据库等编程规范之命名风格 —— 超详细准确无误

&#x1f9f8;欢迎来到dream_ready的博客&#xff0c;&#x1f4dc;相信你对这两篇博客也感兴趣o (ˉ▽ˉ&#xff1b;) &#x1f4dc; 表白墙/留言墙 —— 初级SpringBoot项目&#xff0c;练手项目前后端开发(带完整源码) 全方位全步骤手把手教学 &#x1f4dc; 用户登录前后端…...

编程日记 2023/11/1 7:29:55

有什么可以自动保存微信收到的图片和视频的方法么

8-1 在一些有外勤工作的公司里&#xff0c;经常会需要在外面工作的同事把工作情况的图片发到指定微信或者指定的微信群里&#xff0c;以记录工作进展等&#xff0c;或者打卡等&#xff0c;对于外勤人员来说&#xff0c;也就发个图片的事&#xff0c;但是对于在公司里收图片的人…...

编程日记 2023/11/1 7:28:54

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的？

&#x1f9e0; 智能合约中的数据是如何在区块链中保持一致的&#xff1f; 为什么所有区块链节点都能得出相同结果&#xff1f;合约调用这么复杂&#xff0c;状态真能保持一致吗&#xff1f;本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里&#xf…...

编程新知 2025/7/12 23:55:04

第19节 Node.js Express 框架

Express 是一个为Node.js设计的web开发框架&#xff0c;它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用&#xff0c;和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

编程新知 2025/8/27 10:41:47

脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）

一、数据处理与分析实战 &#xff08;一&#xff09;实时滤波与参数调整 基础滤波操作 60Hz 工频滤波&#xff1a;勾选界面右侧 “60Hz” 复选框&#xff0c;可有效抑制电网干扰&#xff08;适用于北美地区&#xff0c;欧洲用户可调整为 50Hz&#xff09;。 平滑处理&…...

编程新知 2025/7/31 5:34:43

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2025/7/5 11:03:11

shell脚本--常见案例

1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件&#xff1a; 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

编程新知 2025/8/22 22:09:57

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一）

CSI-2 协议详细解析 (一&#xff09; 1. CSI-2层定义&#xff08;CSI-2 Layer Definitions&#xff09; 分层结构 &#xff1a;CSI-2协议分为6层&#xff1a; 物理层&#xff08;PHY Layer&#xff09; &#xff1a; 定义电气特性、时钟机制和传输介质&#xff08;导线&#…...

编程新知 2025/8/22 3:51:45

UE5 学习系列（三）创建和移动物体

这篇博客是该系列的第三篇&#xff0c;是在之前两篇博客的基础上展开&#xff0c;主要介绍如何在操作界面中创建和拖动物体&#xff0c;这篇博客跟随的视频链接如下&#xff1a; B 站视频&#xff1a;s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

编程新知 2025/8/21 4:46:16

linux 错误码总结

1，错误码的概念与作用 在Linux系统中，错误码是系统调用或库函数在执行失败时返回的特定数值，用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递，errno由操作系统维护，保存最近一次发生的错误信息。值得注意的是，errno的值在每次系统调用或函数调用失败时…...

编程新知 2025/8/11 15:02:00

P3 QT项目----记事本（3.8）

3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2025/8/27 3:30:23

三体问题详解

从物理学角度&#xff0c;三体问题之所以不稳定&#xff0c;是因为三个天体在万有引力作用下相互作用&#xff0c;形成一个非线性耦合系统。我们可以从牛顿经典力学出发&#xff0c;列出具体的运动方程&#xff0c;并说明为何这个系统本质上是混沌的&#xff0c;无法得到一般解…...

编程新知 2025/8/18 17:38:23