C++ Dijkstra 最短路径求解算法的两种实现方案
迪杰斯特拉算法(Diikstra) 是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。
核心思想,搜索到某一个顶点后,更新与其相邻顶点的权重。顶点权重的数据含义表示从起始点到此点的最短路径长度(也就是经过的所有边的权重之和)。DJ 算法搜索时,每次选择的下一个顶点是所有权重值最小的顶点,其思想是保证每一次选择的顶点和当前顶点权重都是最短的。所以,DJ是基于贪心思想。
矩阵存储
常规时间复杂度:O(n),可以使用堆优化优先队列,时间复杂度降低到O(logN)。缺点是对于稀疏图而言空间浪费严重。
#include <bits/stdc++.h>
using namespace std;//矩阵,存储图
int graph[100][100];
//顶点、边数
int v,e;
//优先队列,使用数组
int pri[100];
//存储起点到其它顶点之间的最短距离
int dis[100];
//设置无穷大常量
int const INF =INT_MAX;/*
*初始化函数
*/
void init()
{//初始化图中顶点之间的关系for(int i=1; i<=v; i++){for(int j=1; j<=v; j++){if( i==j ){//自己和自己的关系(权重)为 0graph[i][j]=0;}else{//任意两点间的距离为无穷大graph[i][j]=INF;}}}//交互式确定图中顶点之间的关系int f,t,w;for( int i=1; i<=e; i++ ){cin>>f>>t>>w;graph[f][t]=w;}//初始设编号为 1 的顶点为起始点,根据顶点的关系初始化起点到其它顶点之间的距离for(int i=1; i<=v; i++){dis[i]=graph[1][i];}//初始化优先队列(也称为候选队列)for(int i=1; i<=v; i++ ){if(i==1){//起始顶点默认为已经候选pri[i]=1;continue;}//其它顶点都可候选pri[i]=0;}}/*
*
*Dijkstra算法
*/
void dijkstra()
{for(int i=1; i<=v; i++){//从候选队列中选择一个顶点,要求到起始顶点的距离为最近的int u=-1;int mi=INF;for( int j=1; j<=v; j++ ){if(pri[j]==0 && dis[j]<mi){mi=dis[j];u=j;}}if(u!=-1)//找到后设置为已经候选pri[u]=1;else //找不到就结束break;//查找与此候选顶点相邻的顶点,且更新邻接点与起点之间的距离//相当于在此顶点基础上向后延长for( int j=1; j<=v; j++ ){if( graph[u][j]!=INF ){//找到相邻顶点if(dis[j]>dis[u]+graph[u][j] ){//更新dis[j]=dis[u]+graph[u][j];}}}}}/*
*
*显示最后的结果
*/
void show()
{for(int i=1; i<=v; i++){cout<<dis[i]<<"\t";}
}int main()
{cin>>v>>e;init();dijkstra();show();return 0;
}
//测试用例
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
//输出
0 1 8 4 13 17
邻接表
整个时间复杂度可以优化到O(M+N)logN。在最坏的情况下M(边数)就是N(顶点数),这样的话(M+M)logN要比N还要大。但是大多数情况下并不会有那么多边,因此(M+M)logN要比N小很多。
#include <bits/stdc++.h>using namespace std;
/*
* 顶点类型
*/
struct Ver
{//顶点编号int vid=0;//第一个邻接点int head=0;//起点到此顶点的距离(顶点权重),初始为 0 或者无穷大int dis=0;//重载函数bool operator<( const Ver & ver ) const{return this->dis<ver.dis;}void desc(){cout<<vid<<" "<<dis<<endl;}
};/*
* 边
*/
struct Edge
{//邻接点int to;//下一个int next=0;//权重int weight;
};class Graph
{
private:const int INF=INT_MAX;//存储所有顶点Ver vers[100];//存储所有边Edge edges[100];//顶点数,边数int v,e;//起点到其它顶点之间的最短距离int dis[100];//优先队列priority_queue<Ver> proQue;public:Graph( int v,int e ){this->v=v;this->e=e;init();}void init(){for(int i=1;i<=v;i++){//重置顶点信息vers[i].vid=i;vers[i].dis=INF;vers[i].head=0;}int f,t,w;for(int i=1; i<=e; i++){cin>>f>>t>>w;//设置边的信息edges[i].to=t;edges[i].weight=w;//头部插入edges[i].next=vers[f].head;vers[f].head=i;}for(int i=1; i<=v; i++){dis[i]=vers[i].dis;}}void dijkstra(int start){//初始化优先队列,起点到起点的距离为 0vers[start].dis=0;dis[start]=0;proQue.push(vers[start]);while( !proQue.empty() ){//出队列Ver ver=proQue.top();ver.desc();proQue.pop();//找到邻接顶点 i 是边集合索引号for( int i=ver.head; i!=0; i=edges[i].next){int v=edges[i].to;//更新距离if( vers[ v ].dis > ver.dis + edges[i].weight ){vers[ v ].dis = ver.dis+edges[i].weight;dis[ v ]= vers[ v ].dis;//入队列proQue.push( vers[v] );}}}}void show(){for(int i=1; i<=v; i++){cout<<dis[i]<<"\t";}}};int main()
{int v,e;cin>>v>>e;Graph graph(v,e);int s;cin>>s;graph.dijkstra(s);graph.show();return 0;
}
相关文章:

C++ Dijkstra 最短路径求解算法的两种实现方案
迪杰斯特拉算法(Diikstra) 是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。 核心思想,搜索到某一个顶点后,更新与其相邻顶点的权重。顶点权重的数据含义表示从起始点到此点的最短路径长度(也就是经过的…...

因存在色情内容,夸克被罚50万元
媒体经济的繁荣、自媒体、直播等各种形式的信息传播疯狂发展,但是各种形式的信息资源大规模生产时,“色情”,“暴力”的图像和视频不可控的滋生,特别是某些 APP 或浏览器。一旦打开,满屏都是“哥哥,快来啊”…...
汽车EDI:福特Ford EDI项目案例
项目背景 福特(Ford)是世界著名的汽车品牌,为美国福特汽车公司(Ford Motor Company)旗下的众多品牌之一。此前的文章福特FORD EDI需求分析中,我们已经了解了福特Ford EDI 的大致需求,本文将会介…...

正则表达式的使用实例
正则表达式的使用实例 1- 表示2- 实例 1- 表示 1, [:digit:] 表示0-9全部十个数字 //等价于 0123456789, 而不等价于[0123456789] 2, [[:digit:]] 表示任意一个数字 \{m,n\} 表示其前面的字符出现最少m次,最多n次的情况 \{3,\} 其前面的字符出…...
STM智能小车——OLED实现测速小车
目录 1. 测速模块 2. 测试原理和单位换算 3. 定时器和中断实现测速开发和调试代码 4. 小车速度显示在OLED屏 1. 测速模块 用途:广泛用于电机转速检测,脉冲计数,位置限位等。有遮挡,输出高电平;无遮挡,输出低电平接线…...

pod基本概念
目录 pod基本概念 pause容器 Pod分类: Pod容器的分类 1、基础容器(infrastructure container) 2、初始化容器(initcontainers) 3、应用容器(Maincontainer) 镜像拉取策略(im…...

SQL Server 中定时调度调用存储过程
要在SQL中定时调度调用存储过程,你可以使用SQL Server代理(如果你正在使用SQL Server数据库)。下面是一些步骤来配置SQL Server代理以定时调度调用存储过程: 打开SQL Server Management Studio (SSMS) 并连接到你的SQL Server实例…...

SpringCloud(三) Ribbon负载均衡
SpringCloud(二) Eureka注册中心的使用-CSDN博客 在SpringCloud(二)中学习了如何通过Eureka实现服务的注册和发送,从而通过RestTemplate实现不同微服务之间的调用,加上LoadBalance注解之后实现负载均衡,那负载均衡的原理是什么呢? 目录 一, 负载均衡 1.1 负载均衡原理 1.2 源…...

vue2:路由前置守卫无法获取到this.$store.state.xxx
在获取到vuex的数据时候,想在router目录下的index.js文件去获取到vuex仓库中声明的全局变量,但是通过this.$store.stote.xxx去获取的时候,报错提示:$store未定义 一、store/index.js const store new Vuex.Store({state: {// 属…...

Unity的碰撞检测(五)
温馨提示:本文基于前一篇“Unity的碰撞检测(四)”继续探讨两个游戏对象具备刚体的BodyType均为Dynamic,但是Collision Detection属性不同的碰撞检测,阅读本文则默认已阅读前文。 (一)测试说明 在基于两…...
管理)
Flutter笔记:Flutter的应用生命周期状态(lifecycleState)管理
Flutter笔记 Flutter的应用生命周期状态(lifecycleState)管理 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/…...
)
代碼隨想錄算法訓練營|第五十四天|300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组。刷题心得(c++)
讀題 300.最长递增子序列 看完代码随想录之后的想法 思想上很簡單,dp[i]表示i之前的包括i的numbers[i]節尾的最長上升子序列的長度 並且透過兩層迴圈,一層遍歷全部,一層遍歷到i,透過比較當前dp[i]還是dp[j] 1哪個比較大&…...

正点原子嵌入式linux驱动开发——Linux 串口RS232/485/GPS 驱动
串口是很常用的一个外设,在Linux下通常通过串口和其他设备或传感器进行通信,根据 电平的不同,串口分为TTL和RS232。不管是什么样的接口电平,其驱动程序都是一样的,通过外接RS485这样的芯片就可以将串口转换为RS485信号…...
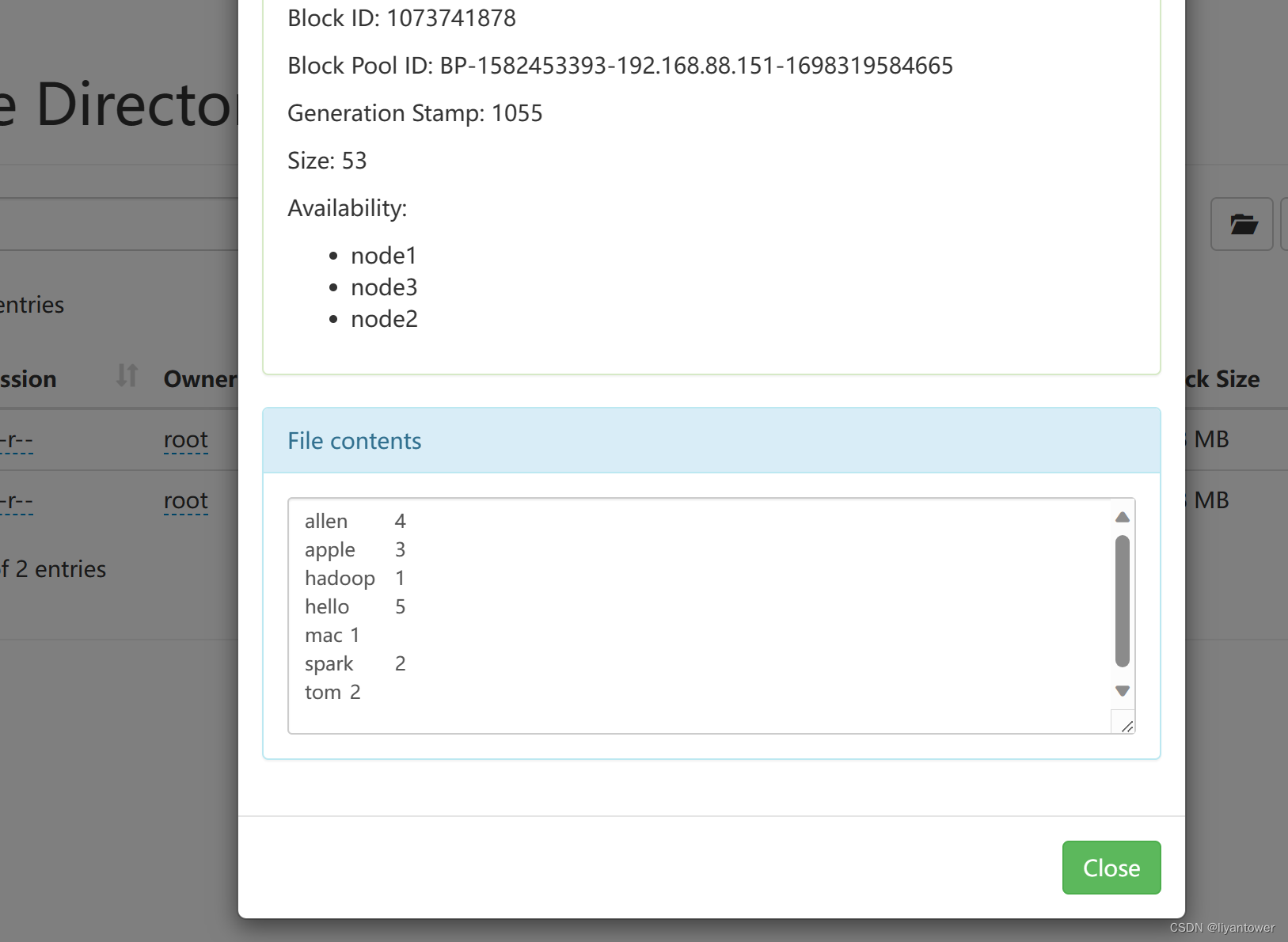
HDFS工作流程和机制
HDFS写数据流程(上传文件) 核心概念--Pipeline管道 HDFS在上传文件写数据过程中采用的一种传输方式。 线性传输:客户端将数据写入第一个数据节点,第一个数据节点保存数据之后再将快复制到第二个节点,第二节点复制给…...

CMMI/ASPICE认证咨询及工具服务
服务概述 质量专家戴明博士的名言“如果你不能描述做事情的过程,那么你不知道你在做什么”。过程是连接有能力的工程师和先进技术的纽带,因此产品开发过程直接决定了产品的质量和研发的效率。 经纬恒润可结合多体系要求,如IATF16949\ISO26262…...
【NI-DAQmx入门】计数器
1.计数器的作用 NI产品的计数器一般来说兼容TTL信号,定义如下:0-0.8V为逻辑低电平,2~5V为高电平,0.8-2V为高阻态,最大上升下降时间为50ns。 计数器可以感测上升沿(从逻辑低到逻辑高的转变)和下降…...

Python爬取读书网的图片链接和书名并保存在数据库中
一个比较基础且常见的爬虫,写下来用于记录和巩固相关知识。 一、前置条件 本项目采用scrapy框架进行爬取,需要提前安装 pip install scrapy# 国内镜像 pip install scrapy -i https://pypi.douban.com/simple 由于需要保存数据到数据库,因…...

js解决加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。 给定两个整数数组 gas 和 cost &…...
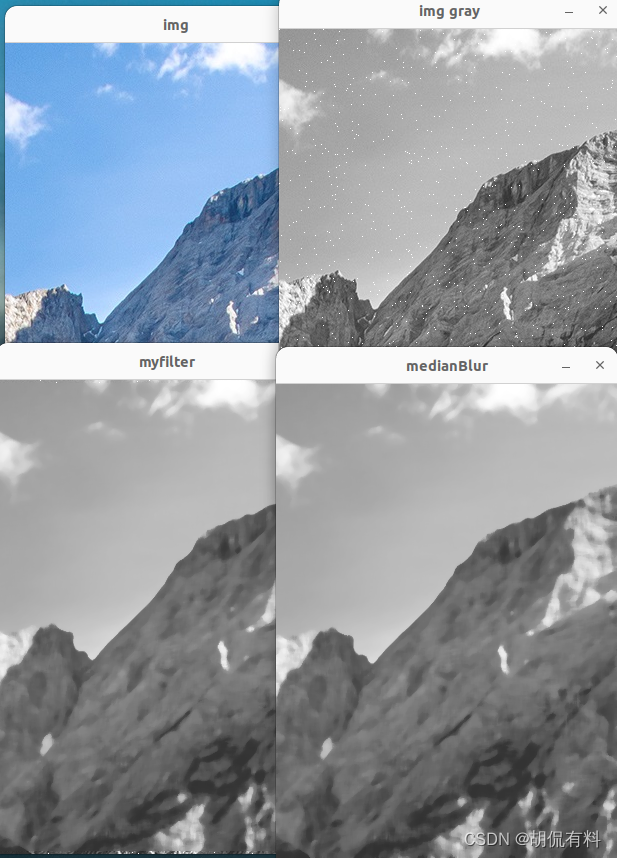
【c++|opencv】二、灰度变换和空间滤波---5.中值滤波
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 1. 中值滤波 #include<iostream> #include<opencv2/opencv.hpp> #include"Salt.h"using namespace cv; using namespace std;voi…...

python之pytorch多进程
目录 1、创建并运行并行进程 2、使用队列(Queue)来共享数据 3、进程池 4、进程锁 5、比较使用多进程和使用单进程执行一段代码的时间消耗 6、共享变量 多进程是计算机科学中的一个术语,它是指同时运行多个进程,这些进程可以…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
