陪诊系统|挂号陪护搭建二开陪诊师入驻就医小程序
我们的陪诊小程序拥有丰富多样的功能,旨在最大程度满足现代人的需求。首先,我们采用了智能排队系统,通过扫描二维码获取排号信息,让您从繁琐的排队过程中解放出来。其次,我们提供了多种支付方式,不仅可以实现挂号费、药费等的在线支付,还可以方便记录和报销相关费用。此外,我们的小程序还提供了医生资讯查询、病历查看、预约挂号等功能,让您能够轻松地获取所需的信息并进行预约。下面小编就给大家介绍下陪诊小程序系统功能。
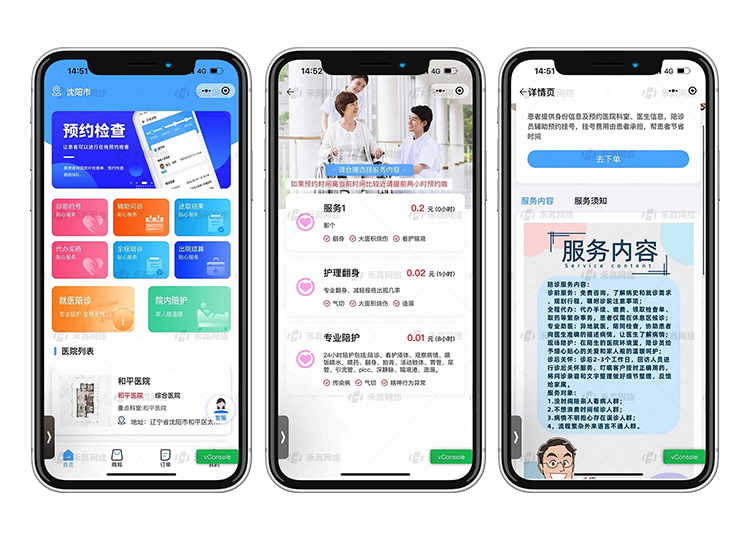
cms后台(系统数据管理):
1、商品管理
2、一级项目二级子项目管理(服务管理)
3、陪诊员信息管理
4、医院管理
5、主管管理
6、陪诊师审核管理
7、订单管理
陪诊小程序客户下单小程序:客户端(用户下单):
1、商品下单,后台发货,收货
2、项目下单(通过地区来选择想要去的医院)
3、订单查看(可看到是否被接单)
4、商品订单查看 陪诊小程序接单小程序:主管,管理员,
陪诊师端:
1、登录,头像昵称获取
2、管理员
3、管理员可指定主管,指定陪诊师
4、审核陪诊师入驻
5、医院信息管理
6、主管
7、派单
8、陪诊师
9、查看指派的单
10、自己接单
陪诊小程序开发设计方面,我们注重用户的使用体验,采用简洁清晰的界面风格,使陪诊小程序的操作更加直观和易用。特别的是,我们还提供了个性化设置,可以根据不同用户的偏好调整界面和功能,让您的陪诊体验更加舒适和贴心。
相关文章:

陪诊系统|挂号陪护搭建二开陪诊师入驻就医小程序
我们的陪诊小程序拥有丰富多样的功能,旨在最大程度满足现代人的需求。首先,我们采用了智能排队系统,通过扫描二维码获取排号信息,让您从繁琐的排队过程中解放出来。其次,我们提供了多种支付方式,不仅可以实…...
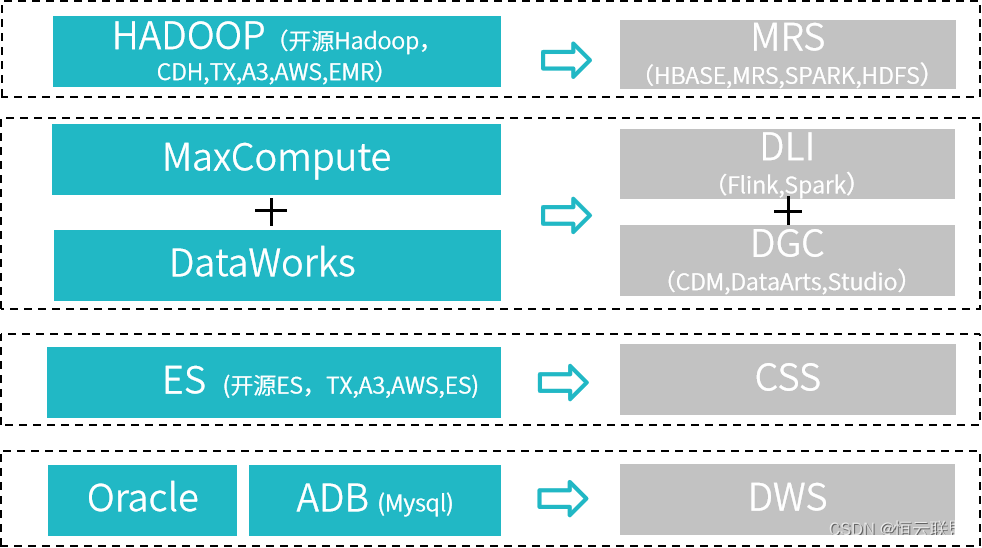
恒驰服务 | 华为云数据使能专家服务offering之大数据建设
恒驰大数据服务主要针对客户在进行智能数据迁移的过程中,存在业务停机、数据丢失、迁移周期紧张、运维成本高等问题,通过为客户提供迁移调研、方案设计、迁移实施、迁移验收等服务内容,支撑客户实现快速稳定上云,有效降低时间成本…...
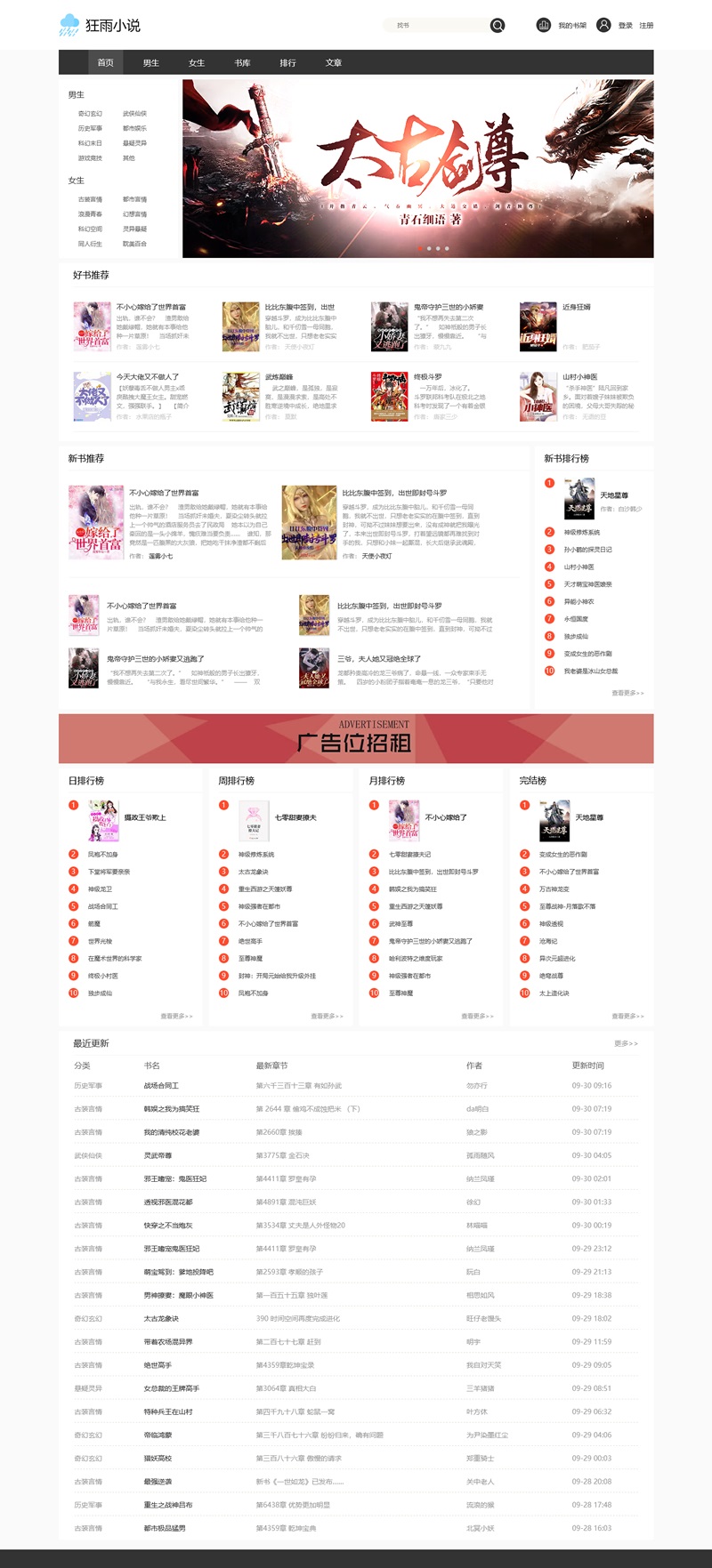
轻量级狂雨小说cms系统源码 v1.5.2 基于ThinkPHP5.1+MySQL
轻量级狂雨小说cms系统源码 v1.5.2 基于ThinkPHP5.1MySQL的技术开发 狂雨小说cms提供一个轻量级小说网站解决方案,基于ThinkPHP5.1MySQL的技术开发。 KYXSCMS,灵活,方便,人性化设计简单易用是最大的特色,是快速架设小说类网站首选…...
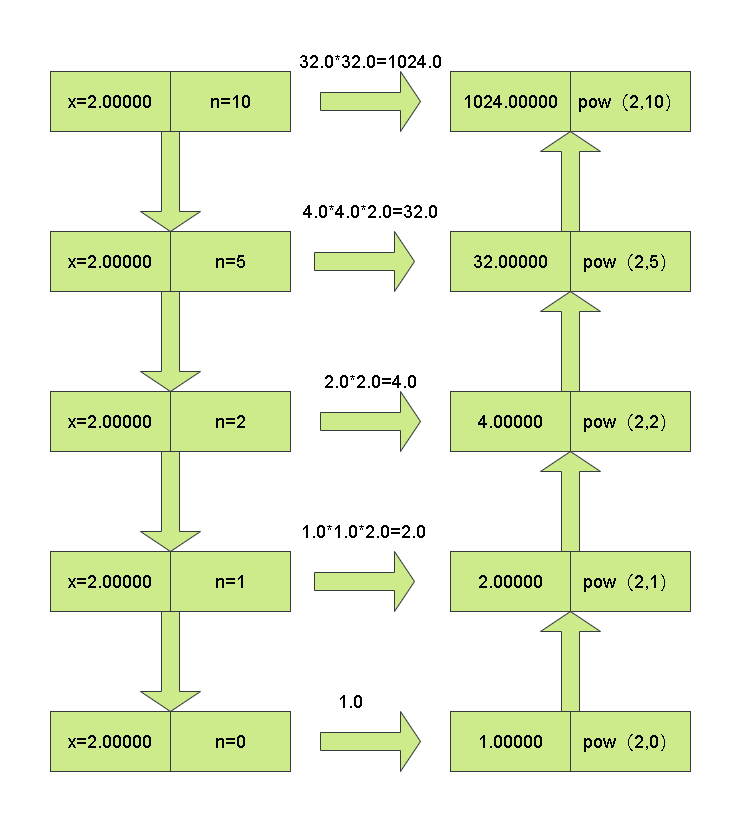
Leetcode刷题详解——Pow(x, n)
1. 题目链接:50. Pow(x, n) 2. 题目描述: 实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。 示例 1: 输入:x 2.00000, n 10 输出:1024.00000示例 2:…...

计算机毕业设计选题推荐-校园失物招领微信小程序/安卓APP-项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

人工智能基础_机器学习011_梯度下降概念_梯度下降步骤_函数与导函数求解最优解---人工智能工作笔记0051
然后我们来看一下梯度下降,这里先看一个叫 无约束最优化问题,,值得是从一个问题的所有可能的备选方案中选最优的方案, 我们的知道,我们的正态分布这里,正规的一个正态分布,还有我们的正规方程,他的这个x,是正规的,比如上面画的这个曲线,他的这个x,就是大于0的对吧,而现实生活…...

开放式耳机能保护听力吗,开放式耳机跟骨传导耳机哪个更好?
如果从严格意义上来讲的话,开放式耳机中的骨传导耳机是能保护听力,现如今的开放式耳机是一个统称,将所有不入耳的类目全部规划到一块。因此在开放式耳机中存在着一些耳机是只能够保持周边环境音,而不是保护听力的。 下面让我来给…...
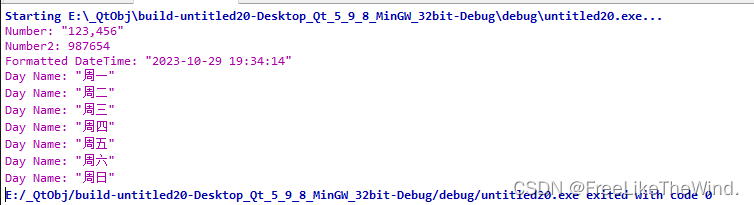
【Qt之QLocale】使用
描述 QLocale类可以在多种语言之间进行数字和字符串的转换。 QLocale类在构造函数中使用语言/国家对进行初始化,并提供类似于QString中的数字转字符串和字符串转数字的转换函数。 示例: QLocale egyptian(QLocale::Arabic, QLocale::Egypt);QString s1 …...
维修服务预约小程序的效果如何
生活服务中维修项目绝对是需求量很高的,如常见的保洁、管道疏通、数码维修、安装、便民服务等,可以说每天都有生意,而对相关维修店企业来说,如何获得更多生意很重要。 接下来让我们看看通过【雨科】平台制作维修服务预约小程序能…...
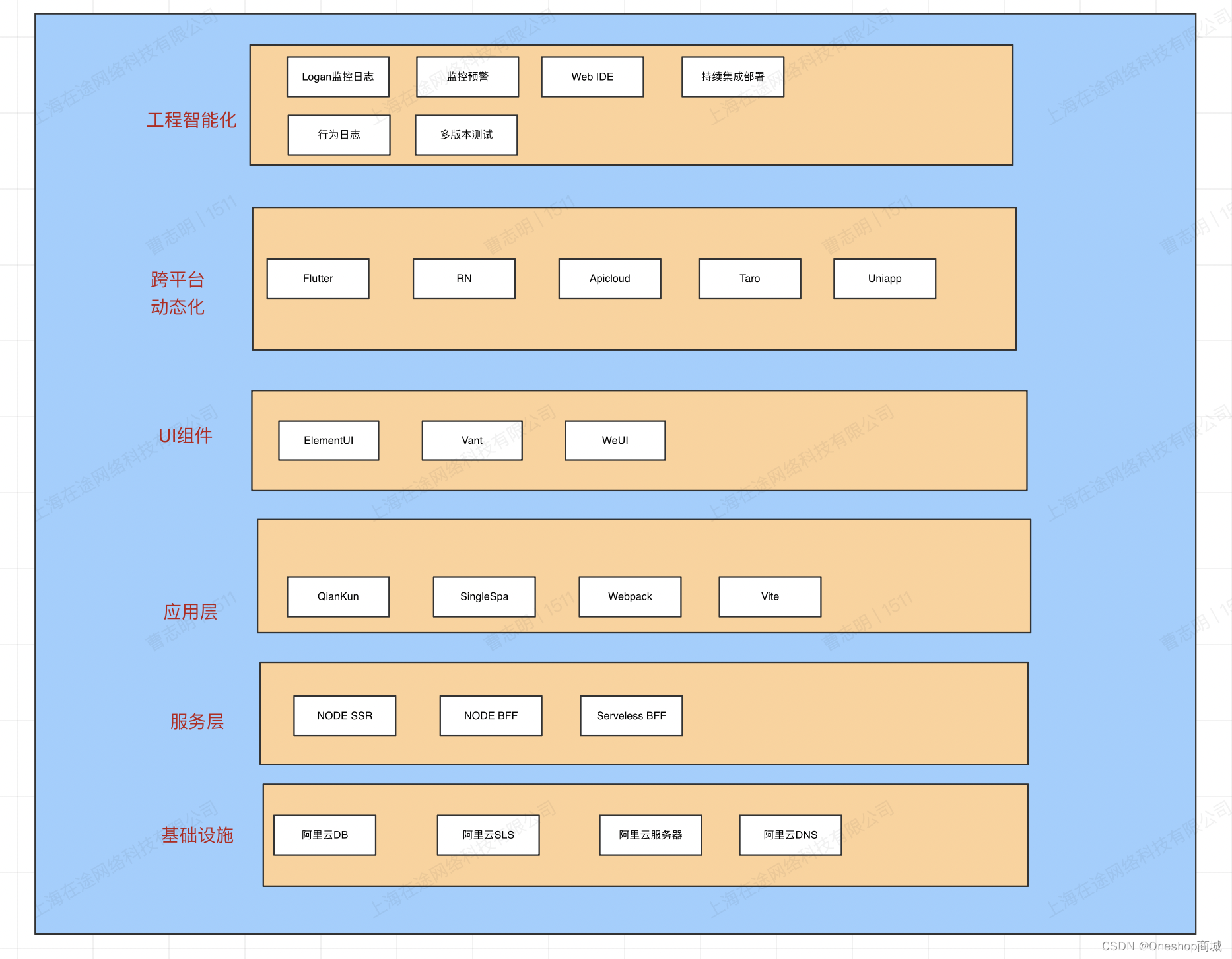
前端架构体系调研整理汇总
1.公司研发人数与前端体系 小型创业公司 前端人数: < 3 人 产品类型: 产品不是非常成熟,比较新颖。 项目流程:不完善,快、紧促,没有固定的时间排期。 技术栈: 没有历史包袱,技…...

DrawerLayout的点击事件会穿透到底部,如何拦截?
DrawerLayout实现侧后,发现了一个问题。点击DrawerLayout的画面,会触发覆盖的底层页面的控件。由此说明点击事件穿透到了底部。但是我只需要触发抽屉布局里的控件,不想触发底层被覆盖的看不见的按钮,由此我想到的时让抽屉页面拦截…...
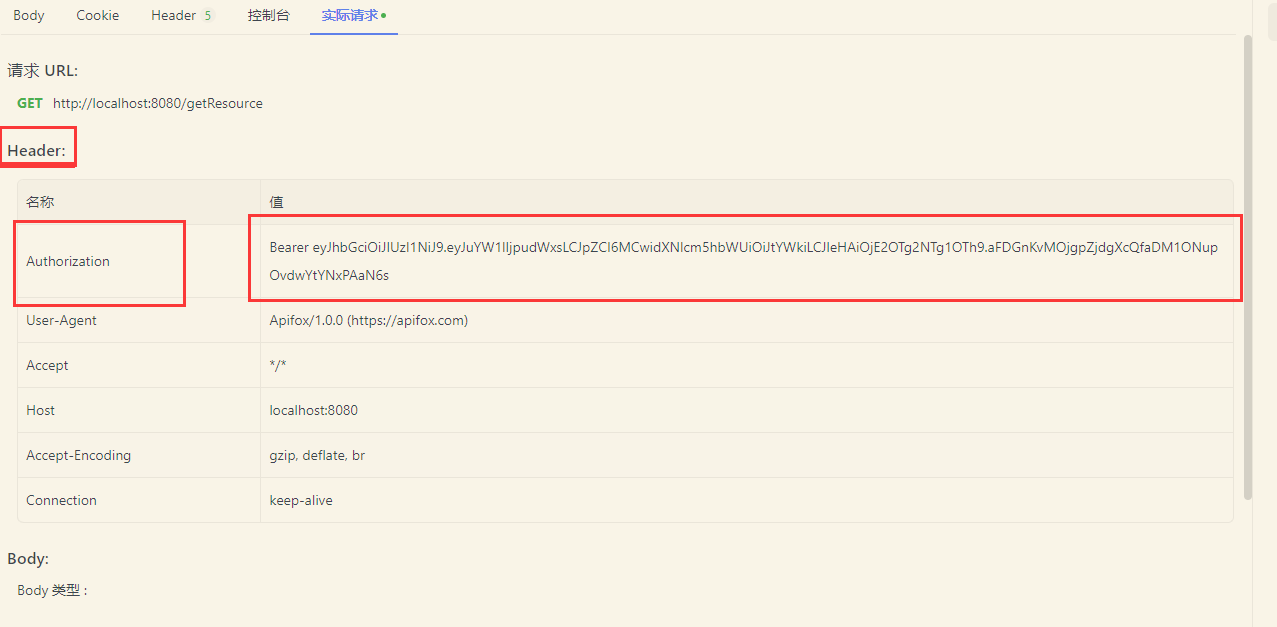
在Spring boot中 使用JWT和过滤器实现登录认证
在Spring boot中 使用JWT和过滤器实现登录认证 一、登录获得JWT 在navicat中运行如下sql,准备一张user表 -- ---------------------------- -- Table structure for t_user -- ---------------------------- DROP TABLE IF EXISTS t_user; CREATE TABLE t_user (id int(11) …...

天堂2如何对版本里面的内容进行修改
天堂2写装备属性的问题 早一点的版本属性都是写在armor文件夹 xml档里,不再写armor里了 armor文件夹里只有防御 HP MP增加量,套装的属性都用一个技能形式写在 skills里了 在配合数据库里一个叫armorsets实现套装属性,拿皇家套做说明。 id 43…...
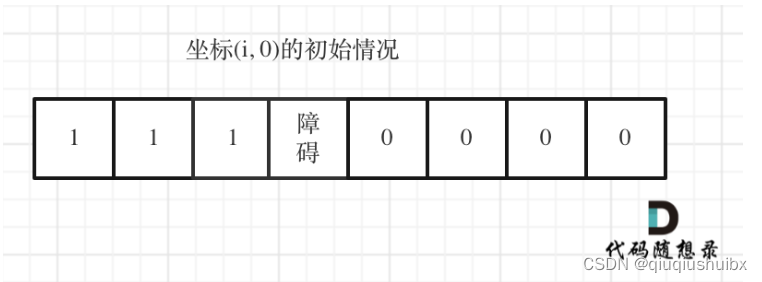
代码随想录Day33 LeetCode T62不同路径 LeetCode T63 不同路径II
前言 动规五部曲 1.确定dp数组含义 2.确定递推公式 3.初始化数组 4.确定遍历方式 5.打印dp数组查看分析问题 LeetCode T62 不同路径 题目链接:62. 不同路径 - 力扣(LeetCode) 题目思路: 注:n行m列而不是m行n列 1.确定dp数组含义 代表到达此下标有多少条…...
【计算机网络】分层模型和应用协议
网络分层模型和应用协议 1. 分层模型 1.1 五层网络模型 网络要解决的问题是:两个程序之间如何交换数据。 四层?五层?七层? 2. 应用层协议 2.1 URL URL(uniform resource locator,统一资源定位符&#…...
Python框架之Flask入门和视图
一、Flask入门和视图 需要安装Pycharm专业版 1. Flask简介 Python后端的2个主流框架 Flask 轻量级框架Django 重型框架 Flask是一个基于Python实现的web开发微框架 官方文档:https://flask.palletsprojects.com/ 中文文档:https://dormousehole.readthe…...

streamWriter.WriteLine
streamWriter.WriteLine写入文件有回车行 using (System.IO.StreamWriter streamWriter new System.IO.StreamWriter("D:\123.txt", false, System.Text.Encoding.Default)) { streamWriter.Write(str.Replace("…...

一键添加色彩变幻效果,视频剪辑从未如此简单!
在视频制作过程中,给视频添加特效是必不可少的环节。而其中,色彩变幻效果作为一种常用的特效,能够为视频增添独特的氛围和视觉冲击力。然而,对于许多初学者来说,如何批量给视频添加色彩变幻效果特效功能却是一个难题。…...
Linux的简介和环境搭建
简介 Linux是一套免费使用和自由传播的类Unix操作系统,是一个基于POSIX和Unix的多用户、多任务、支持多线程和多CPU的操作系统。它能运行主要的Unix工具软件、应用程序和网络协议。它支持32位和64位硬件。Linux继承了Unix以网络为核心的设计思想,是一个…...

你看现在的程序员,是怎么解bug的
大家好,我是伍六七。 干程序员的都会碰到各种各样的 bug,有的 bug 我们看一眼、或者多看几眼就能看出来问题。 但是,也有很多问题,我们看不出来,这个时候,我们不妨把我们的代码扔给 GPT,看看它…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
