06 MIT线性代数-线性无关,基和维数Independence, basis, and dimension
1. 线性无关 Independence
Suppose A is m by n with m<n (more unknowns than equations)
Then there are nonzero solutions to Ax=0
Reason: there will be free variables! A中具有至少一个自由变量,那么Ax=0一定具有非零解。A的列向量可以线性组合得到零向量,所以A的列向量是线性相关的。
independence:vectors X1, X2,...,Xn are independent if no combination gives zero vectors (expect the zero comb. all Ci =0)
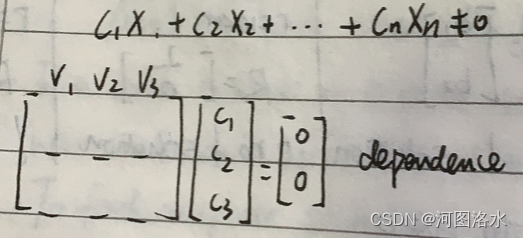
Repeat when v1,v2,..., vn are columns of A
they are independent if nullspace of A is zero vector , rank=n , N(A)={0}, no free variables 若这些向量作为列向量构成矩阵A,则方程Ax=0只有零解x=0,或称矩阵A的零空间只有零向量
they are dependent if Ac=0 for some nonzero C, rank<n , Yes free variables
结论:
此矩阵构成的方程Ax=0必有非零解,即三个向量线性相关
矩阵A的列向量为线性无关,则A所有的列均为主元列,没有自由列,矩阵的秩为n。
若A的列向量为线性相关,则矩阵的秩小于n,并且存在自由列
2. 张成空间 Spanning a space
vectors v1, v2, v3, ..., vn span a space means: The space consists of all combs. of those vectors
3. 基与维数Basis &Dimension
Basis for a space is a sequance of vectors v1, v2, ..., vd with 2 properties:
1. they are independent
2. they span the space
空间的基告诉我们了空间的一切信息
Example: Space is R3
standard: one basis 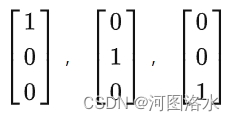
Rn : n vectors give basis if the nxn matrix with those cols is invertible
3.1 子空间的基 Basis for a subspace
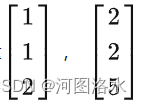 可以张成R3中的一个平面,但是它们无法成为R3空间的一组基
可以张成R3中的一个平面,但是它们无法成为R3空间的一组基
Given a space: Every basis for the space has the same number of vectors (dimension of the space)
3.2 列空间和零空间的基 Basis of a column space and nullspace
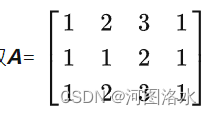
讨论列空间:
矩阵A的四个列向量张成了矩阵A的列空间,其中第3列和第4列与前两列线性相关,而前两个列向量线性无关。因此前两列为主元列。他们组成了列空间C(A)的一组基。矩阵的秩为2。
rank矩阵的秩r=# of pivot columns 矩阵主元列的数目=dimension of C(A)列空间的维数
讨论零空间:
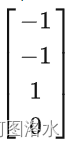 必然在零空间N(A)之内
必然在零空间N(A)之内
dim N(A)零空间的维数=自由列的数目# of free variables=n-r
相关文章:

06 MIT线性代数-线性无关,基和维数Independence, basis, and dimension
1. 线性无关 Independence Suppose A is m by n with m<n (more unknowns than equations) Then there are nonzero solutions to Ax0 Reason: there will be free variables! A中具有至少一个自由变量,那么Ax0一定具有非零解。A的列向量可以线性组合得到零向…...
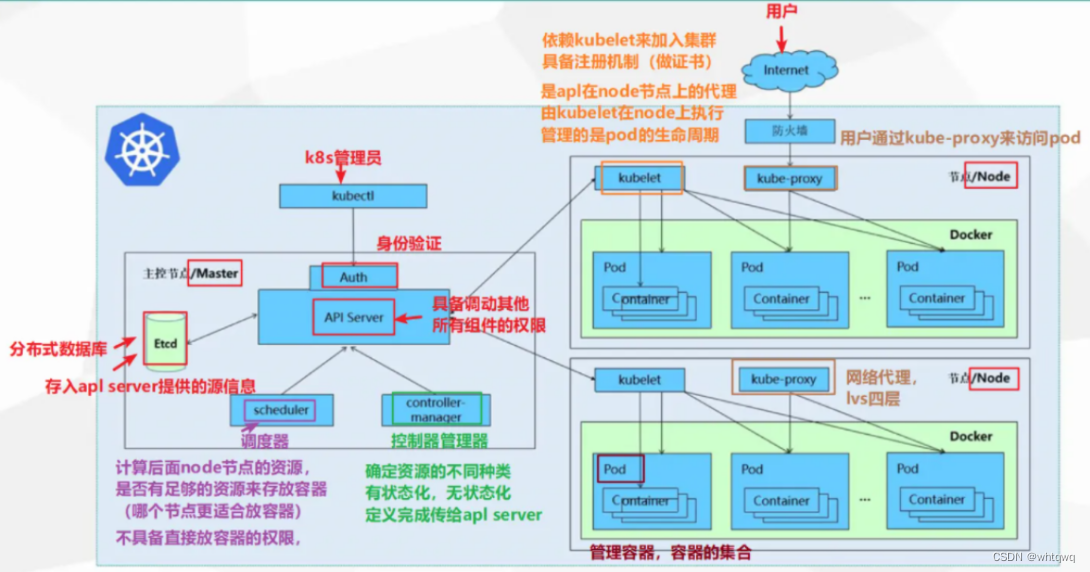
Kubernetes 概述以及Kubernetes 集群架构与组件
目录 Kubernetes概述 K8S 是什么 为什么要用 K8S K8S 的特性 Kubernetes 集群架构与组件 核心组件 Master 组件 Node 组件 编辑 Kubernetes 核心概念 常见的K8S按照部署方式 Kubernetes概述 K8S 是什么 K8S 的全称为 Kubernetes,Kubernetes 是一个可移植、可扩…...

GZ035 5G组网与运维赛题第9套
2023年全国职业院校技能大赛 GZ035 5G组网与运维赛项(高职组) 赛题第9套 一、竞赛须知 1.竞赛内容分布 竞赛模块1--5G公共网络规划部署与开通(35分) 子任务1:5G公共网络部署与调试(15分) 子…...

使用Jasypt3.0.3版本对SpringBoot配置文件加密
时间 2023-11-01 使用Jasypt3.0.3版本对SpringBoot配置文件加密 目录 引入依赖使用密钥生成密文配置yml验证是否自动解密 引入依赖 <!--yml 文件加解密--><dependency><groupId>com.github.ulisesbocchio</groupId><artifactId>jasypt-spring-b…...

生成一篇博客,详细讲解springboot的单点登录功能,有流程图,有源码demo
SpringBoot是目前非常流行的一个Java开发框架,它以简洁的配置和快速的开发效率著称。在实际应用中,单点登录是一个非常重要的功能,它可以让用户在多个应用系统中使用同一个账号登录,提高用户体验和安全性。本文将详细讲解如何在Sp…...
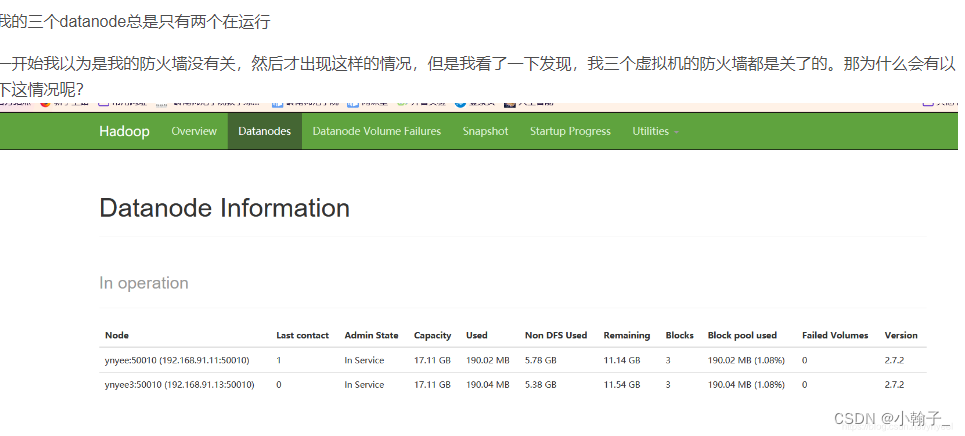
Hadoop、Hive安装
一、 工具 Linux系统:Centos,版本7.0及以上 JDK:jdk1.8 Hadoop:3.1.3 Hive:3.1.2 虚拟机:VMware mysql:5.7.11 工具下载地址: https://pan.baidu.com/s/1JYtUVf2aYl5–i7xO6LOAQ 提取码: xavd…...

PHP自定义函数--输入起始日期和解算日期返回日期差几天和 上一个周期的起始结束日期
/** 日期差几天* param beginDate:2018-01-26 endDatee:2018-01-26* return int days* */ function dateDiff($beginDate, $endDate) {$diff date_diff(date_create($beginDate), date_create($endDate))->format(%R%a);return (int)$diff; }/** 返回上一周期的起始和结束日…...

.net 7 上传文件踩坑
(Name “file”) 没加上这个传不进文件 /// <summary>/// 上传单个文件/// </summary>/// <param name"formFile"></param>/// <returns></returns>[HttpPost("UploadFiles")][FunctionAttribute(MuType.Btn, "…...
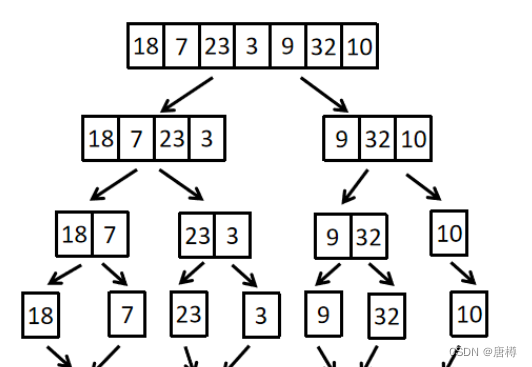
C++基础算法④——排序算法(快速、归并附完整代码)
快速排序 快速排序是对冒泡排序的一种改进。 它的基本思想是:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行快速排序,以达到整个序列有序。 假设我们现在对 …...

高防CDN如何在防护cc上大显神通
高级防御CDN(Content Delivery Network)在对抗CC(HTTP Flood)攻击方面扮演着关键的角色,具备以下重要职能和作用: 流量分散:CC攻击的目标是通过大规模的HTTP请求使服务器过载,从而导…...

解决CSS中height:100%失效的问题
出现BUG的场景,点击退出到登录页面,发现高度不对 上面出现了一种只是占了内容的高度,没有占满100%,为什么会出现这种情况呐? 让div的height"100%",执行网页时,css先执行到࿰…...

小红书穿搭类种草营销怎么做?纯干货
在众多营销方式中,穿搭类种草营销以其独特的优势在小红书平台上崭露头角。穿搭类种草营销,以其独特的优势,成为了品牌和商家推广产品的重要方式。其优势主要体现在以下几个方面: 1. 高度相关性:小红书平台的用户主要是…...

什么是ARFF文件,以.arff结尾
关于arff,主要涉及三个输入类:概念、实例和属性。 1.概念简单而言就是需要被处理的东西, 2. 实例这个词有些陌生,但是可以大致认为其为样本, 3. 属性就是数据表中的一列。 为什么要用arff?(arff介绍&#x…...

华为OD机考算法题:计算疫情扩散时间
题目部分 题目计算疫情扩散时间难度难题目说明在一个地图中(地图由 n * n 个区域组成)有部分区域被感染病菌感染区域每天都会把周围(上下左右)的4个区域感染。 请根据给定的地图计算多少天以后,全部区域都会被感染。 如果初始地图上所有区域全部都被感染࿰…...
29岁从事功能测试5年被辞,面试4个月还没到工作......
最近一个32岁的老同学因为被公司辞退,聊天过程中找我倾诉,所以写下了这篇文章。 他是15年二本毕业,学的园林专业,人属于比较懒的那种,不爱学习,专业学的也一般。实习期间通过校招找到了一份对口的工作。但…...

再记【fatal error C1001: 内部编译器错误】的一个原因
平台:Windows 11、Visual Studio 2022 报错信息 已启动生成... 1>------ 已启动生成: 项目: PointMatchingModel, 配置: Debug x64 ------ 1>PointMatchingModel.cpp 1>C:\tools\vcpkg\installed\x64-windows\include\pcl\registration\impl\ia_fpcs.hpp…...

数据分析、大数据分析和人工智能之间的区别
数据分析、大数据分析和人工智能近年来十分热门,三者之间看起来有相似之处,也有不同之处。今天就来谈谈三者间的区别。 数据分析 数据分析是指对数据进行分析,从中提取有价值的信息,以支持企业或组织的决策制定。数据分析可以针对…...
Spring系列之基础
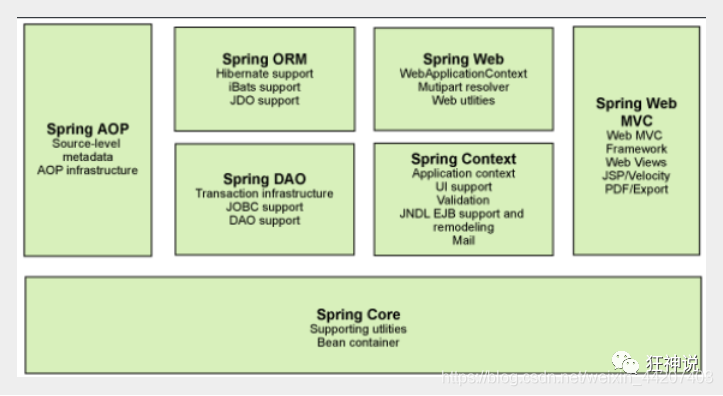
目录 Spring概述 Spring的优点 Spring Framework的组成 总结 Spring概述 Spring 是目前主流的 Java Web 开发框架,是 Java 世界最为成功的框架。该框架是一个轻量级的开源框架,具有很高的凝聚力和吸引力。它以Ioc(控制反转)和…...
Android开发知识学习——TCP / IP 协议族
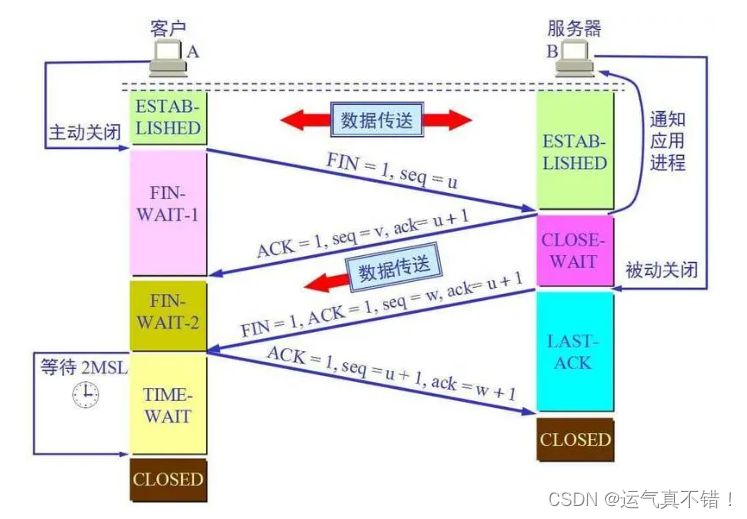
文章目录 学习资源来自:扔物线TCP / IP 协议族TCP连接TCP 连接的建立与关闭TCP 连接的建立为什么要三次握手? TCP 连接的关闭为什么要四次挥手? 为什么要⻓连接? 常见面试题课后题 学习资源来自:扔物线 TCP / IP 协议…...

思维训练 第四课 省略句
系列文章目录 文章目录 系列文章目录前言一、省略的十五种情况1.并列复合句中某些相同成分的省略2.在用when, while, if, as if, though, although, as ,until, whether等连词引导的状语从句中,如果谓语有be,而主语又跟主句的主语相同或是(从句主语是&am…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
