【数据结构】数组和字符串(七):特殊矩阵的压缩存储:三元组表的转置、加法、乘法操作
文章目录
- 4.2.1 矩阵的数组表示
- 4.2.2 特殊矩阵的压缩存储
- a. 对角矩阵的压缩存储
- b~c. 三角、对称矩阵的压缩存储
- d. 稀疏矩阵的压缩存储——三元组表
- 4.2.3三元组表的转置、加法、乘法、操作
- 转置
- 加法
- 乘法
- 算法测试
- 实验结果
- 代码整合
4.2.1 矩阵的数组表示
【数据结构】数组和字符串(一):矩阵的数组表示
4.2.2 特殊矩阵的压缩存储
矩阵是以按行优先次序将所有矩阵元素存放在一个一维数组中。但是对于特殊矩阵,如对称矩阵、三角矩阵、对角矩阵和稀疏矩阵等, 如果用这种方式存储,会出现大量存储空间存放重复信息或零元素的情况,这样会造成很大的空间浪费。为节约存储空间和算法(程序)运行时间,通常会采用压缩存储的方法。
- 对角矩阵:指除了主对角线以外的元素都为零的矩阵,即对 任意 i ≠ j (1≤ i , j ≤n),都有M(i, j)=0。由于只有主对角线上有非零元素,只需存储主对角线上的元素即可。
- 三角矩阵:指上三角或下三角的元素都为零的矩阵。同样地,只需存储其中一部分非零元素,可以节省存储空间。
- 对称矩阵:指矩阵中的元素关于主对角线对称的矩阵。由于对称矩阵的非零元素有一定的规律,可以只存储其中一部分元素,从而减少存储空间。
- 稀疏矩阵:指大部分元素为零的矩阵。传统的按行优先次序存储方法会浪费大量空间来存储零元素,因此采用压缩存储的方法更为合适。常见的压缩存储方法有:压缩稠密行(CSR)、压缩稠密列(CSC)、坐标列表(COO)等。
a. 对角矩阵的压缩存储
【数据结构】数组和字符串(二):特殊矩阵的压缩存储:对角矩阵——一维数组
b~c. 三角、对称矩阵的压缩存储
【数据结构】数组和字符串(三):特殊矩阵的压缩存储:三角矩阵、对称矩阵——一维数组
d. 稀疏矩阵的压缩存储——三元组表
对于稀疏矩阵的压缩存储,由于非零元素的个数远小于零元素的个数,并且非零元素的分布没有规律,无法简单地利用一维数组和映射公式来实现压缩存储。针对稀疏矩阵,通常采用特定的数据结构来进行压缩存储,以减少存储空间的占用。
一种常见的稀疏矩阵压缩存储方法是使用"三元组"表示法,也称为COO(Coordinate)格式,只存储非零元素的值以及它们的行列坐标。通过使用三元组(Triplet)来表示非零元素的位置和值,每个三元组包含三个信息:非零元素的行索引、非零元素的列索引以及非零元素的值。
【数据结构】数组和字符串(四):特殊矩阵的压缩存储:稀疏矩阵——三元组表
4.2.3三元组表的转置、加法、乘法、操作
转置
假设稀疏矩阵存储在一个三元组表a中,且A的非零元素个数为count,算法Transpose求A的转置矩阵并将其保存在三元组表b中。
- 算法的主要思想是针对每个列号k(k=0, 2,… , n-1)对a进行扫描,考察a中是否有列号为k的结点(注意:列号为k的结点可能不止一个),若有,记为a[u](假定a[u]在a中的行号为i ),将a[u]依次保存在b的b[w] 中,则row(b[w])=k,col(b[w])=i,value(b[w]) =value(a[u]).

TripletTable matrixTranspose(TripletTable* table) {TripletTable result;initTable(&result, table->cols, table->rows); // 转置后的矩阵行列互换int j = 0;for (int k = 0; k < table->cols; k++) {for (int i = 0; i < table->length; i++) {Triple* element = &(table->data[i]);if (element->col == k) {insertElement(&result, k, element->row, element->value);
// result.data[j].row = k; // 该元素在result中的行号应为k
// result.data[j].col = element->row; // 该元素在result中的列号应为其在table中的行号
// result.data[j].value = element->value;j++; // 考察result中的下一个结点result.length = j; // 更新result的长度}}
// printf("\n");
// displayMatrix(&result);}return result;
}
matrixTranspose函数实现稀疏矩阵的转置操作:
- 首先,创建一个新的
TripletTable变量result,用于存储输入矩阵的转置。 - 使用
initTable函数初始化result,将其行数设置为输入矩阵的列数,列数设置为输入矩阵的行数。 - 使用一个循环遍历输入矩阵的所有元素:
- 对于每个元素,将其行号作为转置后矩阵中的列号,列号作为转置后矩阵中的行号,并将值保持不变。
- 将转置后的元素插入到
result中。
- 返回
result作为输入矩阵的转置。
加法
TripletTable matrixAddition(TripletTable* table1, TripletTable* table2) {TripletTable result;initTable(&result, table1->rows, table1->cols);int i = 0, j = 0;while (i < table1->length && j < table2->length) {Triple* element1 = &(table1->data[i]);Triple* element2 = &(table2->data[j]);if (element1->row < element2->row || (element1->row == element2->row && element1->col < element2->col)) {insertElement(&result, element1->row, element1->col, element1->value);i++;} else if (element1->row > element2->row || (element1->row == element2->row && element1->col > element2->col)) {insertElement(&result, element2->row, element2->col, element2->value);j++;} else {int sum = element1->value + element2->value;if (sum != 0) {insertElement(&result, element1->row, element1->col, sum);}i++;j++;}}while (i < table1->length) {Triple* element1 = &(table1->data[i]);insertElement(&result, element1->row, element1->col, element1->value);i++;}while (j < table2->length) {Triple* element2 = &(table2->data[j]);insertElement(&result, element2->row, element2->col, element2->value);j++;}return result;
}
matrixAddition函数实现稀疏矩阵的加法操作:
- 创建一个新的
TripletTable变量result,用于存储两个输入矩阵的和。 - 使用
initTable函数初始化result,将其行数和列数设置为与输入矩阵相同。 - 使用两个指针
i和j分别指向两个输入矩阵的元素。 - 通过比较当前元素的行号和列号,以及使用循环遍历的方式,将两个输入矩阵的元素逐个比较并进行相应的操作:
- 如果第一个矩阵的元素在行号和列号上小于第二个矩阵的元素,将第一个矩阵的元素插入到
result中,并增加指向第一个矩阵元素的指针i。 - 如果第一个矩阵的元素在行号和列号上大于第二个矩阵的元素,将第二个矩阵的元素插入到
result中,并增加指向第二个矩阵元素的指针j。 - 如果两个矩阵的元素在行号和列号上相等,将它们的值相加,并将结果插入到
result中。然后,增加指向两个矩阵元素的指针i和j。
- 如果第一个矩阵的元素在行号和列号上小于第二个矩阵的元素,将第一个矩阵的元素插入到
- 处理完所有元素后,将剩余的未处理元素插入到
result中。 - 返回
result作为两个输入矩阵的和。
乘法
TripletTable matrixMultiplication(TripletTable* table1, TripletTable* table2) {TripletTable result;initTable(&result, table1->rows, table2->cols);int matrix[table1->rows][table2->cols];for (int i = 0; i < table1->rows; i++) {for (int j = 0; j < table2->cols; j++) {matrix[i][j] = 0;}}for (int i = 0; i < table1->length; i++) {Triple* element1 = &(table1->data[i]);for (int j = 0; j < table2->length; j++) {Triple* element2 = &(table2->data[j]);if (element1->col == element2->row) {matrix[element1->row][element2->col] += element1->value * element2->value;}}}for (int i = 0; i < table1->rows; i++) {for (int j = 0; j < table2->cols; j++) {if (matrix[i][j] != 0) {insertElement(&result, i, j, matrix[i][j]);}}}return result;
}
matrixMultiplication函数实现稀疏矩阵的乘法操作:
- 创建一个新的
TripletTable变量result,用于存储两个输入矩阵的乘积。 - 使用
initTable函数初始化result,将其行数设置为第一个输入矩阵的行数,列数设置为第二个输入矩阵的列数。 - 创建一个临时的二维数组
matrix,用于存储两个输入矩阵相乘的结果。 - 将
matrix中的所有元素初始化为0。 - 使用两个嵌套的循环遍历第一个输入矩阵的所有元素:
- 对于每个元素,使用另一个嵌套的循环遍历第二个输入矩阵的所有元素。
- 如果第一个矩阵的元素的列号等于第二个矩阵的元素的行号,将它们的值相乘,并将结果累加到
matrix中对应位置的元素上。
- 遍历
matrix中的所有元素,将非零元素插入到result中。 - 返回
result作为两个输入矩阵的乘积。
算法测试
int main() {TripletTable matrixA, matrixB;initTable(&matrixA, 3, 3);initTable(&matrixB, 3, 3);// Insert elements into matrix AinsertElement(&matrixA, 0, 0, 1);insertElement(&matrixA, 0, 2, 2);insertElement(&matrixA, 1, 1, 3);insertElement(&matrixA, 2, 0, 4);insertElement(&matrixA, 2, 2, 5);// Insert elements into matrix BinsertElement(&matrixB, 0, 1, 6);insertElement(&matrixB, 1, 0, 7);insertElement(&matrixB, 1, 2, 8);insertElement(&matrixB, 2, 1, 9);printf("Matrix A:\n");displayMatrix(&matrixA);printf("\nMatrix B:\n");displayMatrix(&matrixB);TripletTable matrixC = matrixAddition(&matrixA, &matrixB);printf("\nMatrix A + B:\n");displayMatrix(&matrixC);TripletTable matrixD = matrixTranspose(&matrixA);printf("\nTranspose of Matrix A:\n");displayMatrix(&matrixD);TripletTable matrixE = matrixMultiplication(&matrixA, &matrixB);printf("\nMatrix A * B:\n");displayMatrix(&matrixE);return 0;
}
实验结果
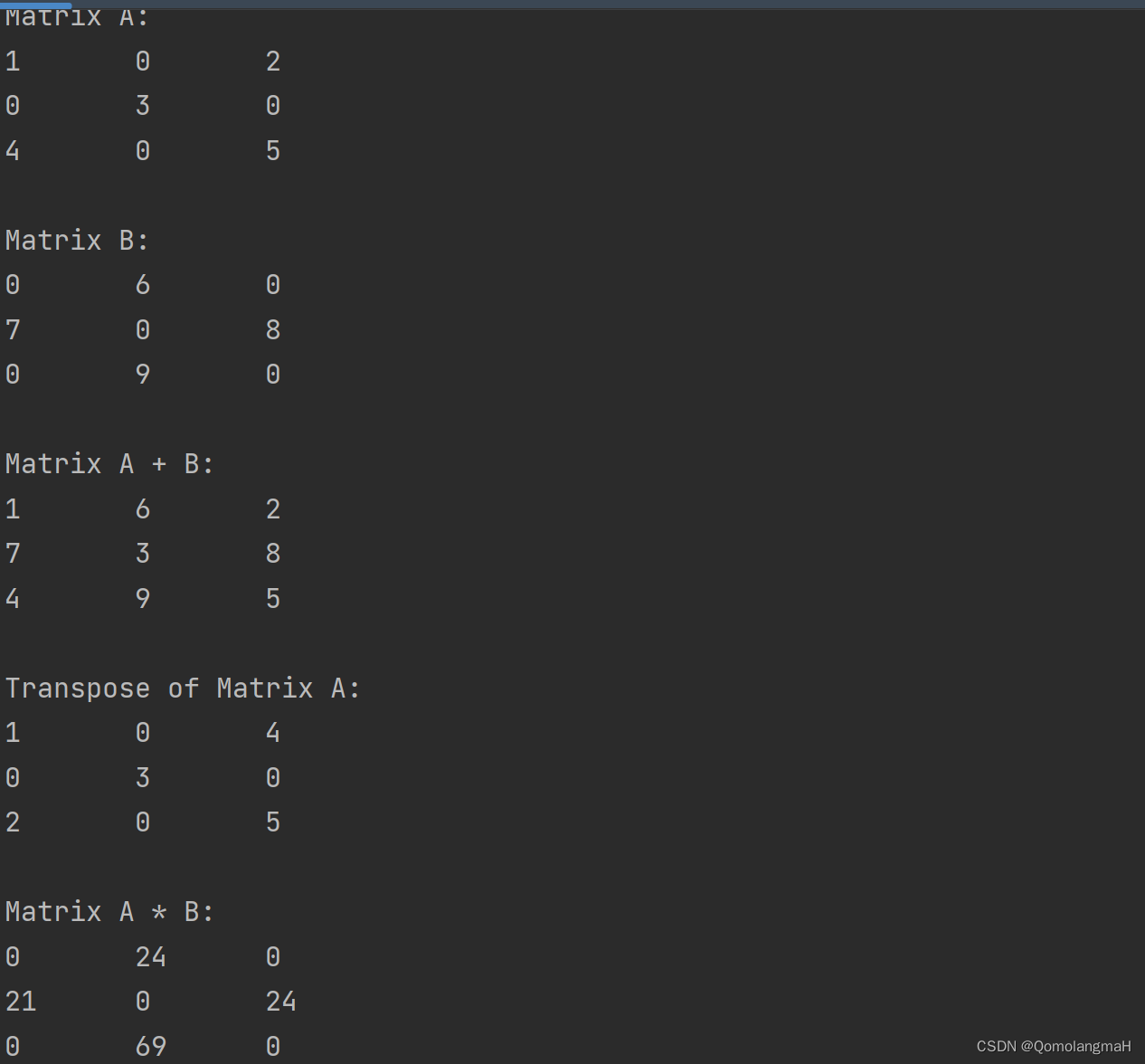
代码整合
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_SIZE 10typedef struct {int row;int col;int value;
} Triple;typedef struct {Triple data[MAX_SIZE];int rows;int cols;int length;
} TripletTable;void initTable(TripletTable* table, int rows, int cols) {table->rows = rows;table->cols = cols;table->length = 0;memset(table->data, 0, sizeof(Triple) * MAX_SIZE); // 新添加
}void insertElement(TripletTable* table, int row, int col, int value) {if (table->length >= MAX_SIZE) {printf("Table is full. Cannot insert more elements.\n");return;}Triple* element = &(table->data[table->length]);element->row = row;element->col = col;element->value = value;table->length++;
}void displayMatrix(TripletTable* table) {int matrix[table->rows][table->cols];for (int i = 0; i < table->rows; i++) {for (int j = 0; j < table->cols; j++) {matrix[i][j] = 0;}}
// printf("Row\tColumn\tValue\n");for (int i = 0; i < table->length; i++) {Triple* element = &(table->data[i]);
// printf("%d\t%d\t%d\n", element->row, element->col, element->value);matrix[element->row][element->col] = element->value;}// printf("Matrix:\n");for (int i = 0; i < table->rows; i++) {for (int j = 0; j < table->cols; j++) {printf("%d\t", matrix[i][j]);}printf("\n");}
}
TripletTable matrixAddition(TripletTable* table1, TripletTable* table2) {TripletTable result;initTable(&result, table1->rows, table1->cols);int i = 0, j = 0;while (i < table1->length && j < table2->length) {Triple* element1 = &(table1->data[i]);Triple* element2 = &(table2->data[j]);if (element1->row < element2->row || (element1->row == element2->row && element1->col < element2->col)) {insertElement(&result, element1->row, element1->col, element1->value);i++;} else if (element1->row > element2->row || (element1->row == element2->row && element1->col > element2->col)) {insertElement(&result, element2->row, element2->col, element2->value);j++;} else {int sum = element1->value + element2->value;if (sum != 0) {insertElement(&result, element1->row, element1->col, sum);}i++;j++;}}while (i < table1->length) {Triple* element1 = &(table1->data[i]);insertElement(&result, element1->row, element1->col, element1->value);i++;}while (j < table2->length) {Triple* element2 = &(table2->data[j]);insertElement(&result, element2->row, element2->col, element2->value);j++;}return result;
}TripletTable matrixMultiplication(TripletTable* table1, TripletTable* table2) {TripletTable result;initTable(&result, table1->rows, table2->cols);int matrix[table1->rows][table2->cols];for (int i = 0; i < table1->rows; i++) {for (int j = 0; j < table2->cols; j++) {matrix[i][j] = 0;}}for (int i = 0; i < table1->length; i++) {Triple* element1 = &(table1->data[i]);for (int j = 0; j < table2->length; j++) {Triple* element2 = &(table2->data[j]);if (element1->col == element2->row) {matrix[element1->row][element2->col] += element1->value * element2->value;}}}for (int i = 0; i < table1->rows; i++) {for (int j = 0; j < table2->cols; j++) {if (matrix[i][j] != 0) {insertElement(&result, i, j, matrix[i][j]);}}}return result;
}TripletTable matrixTranspose(TripletTable* table) {TripletTable result;initTable(&result, table->cols, table->rows); // 转置后的矩阵行列互换int j = 0;for (int k = 0; k < table->cols; k++) {for (int i = 0; i < table->length; i++) {Triple* element = &(table->data[i]);if (element->col == k) {insertElement(&result, k, element->row, element->value);
// result.data[j].row = k; // 该元素在result中的行号应为k
// result.data[j].col = element->row; // 该元素在result中的列号应为其在table中的行号
// result.data[j].value = element->value;j++; // 考察result中的下一个结点result.length = j; // 更新result的长度}}
// printf("\n");
// displayMatrix(&result);}return result;
}int main() {TripletTable matrixA, matrixB;initTable(&matrixA, 3, 3);initTable(&matrixB, 3, 3);// Insert elements into matrix AinsertElement(&matrixA, 0, 0, 1);insertElement(&matrixA, 0, 2, 2);insertElement(&matrixA, 1, 1, 3);insertElement(&matrixA, 2, 0, 4);insertElement(&matrixA, 2, 2, 5);// Insert elements into matrix BinsertElement(&matrixB, 0, 1, 6);insertElement(&matrixB, 1, 0, 7);insertElement(&matrixB, 1, 2, 8);insertElement(&matrixB, 2, 1, 9);printf("Matrix A:\n");displayMatrix(&matrixA);printf("\nMatrix B:\n");displayMatrix(&matrixB);TripletTable matrixC = matrixAddition(&matrixA, &matrixB);printf("\nMatrix A + B:\n");displayMatrix(&matrixC);TripletTable matrixD = matrixTranspose(&matrixA);printf("\nTranspose of Matrix A:\n");displayMatrix(&matrixD);TripletTable matrixE = matrixMultiplication(&matrixA, &matrixB);printf("\nMatrix A * B:\n");displayMatrix(&matrixE);return 0;
}
相关文章:

【数据结构】数组和字符串(七):特殊矩阵的压缩存储:三元组表的转置、加法、乘法操作
文章目录 4.2.1 矩阵的数组表示4.2.2 特殊矩阵的压缩存储a. 对角矩阵的压缩存储b~c. 三角、对称矩阵的压缩存储d. 稀疏矩阵的压缩存储——三元组表4.2.3三元组表的转置、加法、乘法、操作转置加法乘法算法测试实验结果代码整合 4.2.1 矩阵的数组表示 【数据结构】数组和字符串…...

Spring底层原理(四)
Spring底层原理(四) 本章内容 模拟实现Spring中的几个常见BeanFactory后置处理器 常见的BeanFactory后置处理器 GenericApplicationContext context new GenericApplicationContext(); context.registerBean("config",Config.class); context.registerBean(Conf…...

Android 14 rook替代Postern进行中间人抓包
以下是关于使用Brook替代Postern进行中间人抓包的说明: 先来解释下,为什么用Postern而不用fd,fd属于代理抓包。Postern属于是模拟出来一张虚拟网卡抓包。性质不一样,所以害怕大哥问我。我就先放在这里 在Android 14及之前的版本中…...

[rancher] rancher部署和使用的一些思考
最近因为工作需要,学习调研rancher的使用 k8s作为主流微服务部署的基础,已经逐渐在工作中普及。但是k8s dashboard用于生产管理,还是有所欠缺:我们需要一个k8s之上的管理平台。经过调研,目前rancher已经迭代开发至v2.8…...

迅镭激光董事长颜章健荣膺“2023年如皋市科技强企人物”!
10月28日,2023如皋科技人才洽谈会开幕式在如皋隆重举行。江苏省科学技术厅副厅长、党组成员蒋洪,江苏省商务厅副厅长、党组成员孙津,中共南通市委副书记、政法委书记沈雷,中共如皋市市委书记何益军,中共如皋市委副书记…...

专业医学病例翻译公司推荐
我们知道,医学病例翻译在涉外看病的患者中具有广泛的应用,它可以帮助医生快速了解患者的病情,为治疗和药物处方提供关键信息。因此,对于出国看病的患者,医学病例翻译便成了不可或缺的重要工具。 翻译医学病例不仅要求译…...
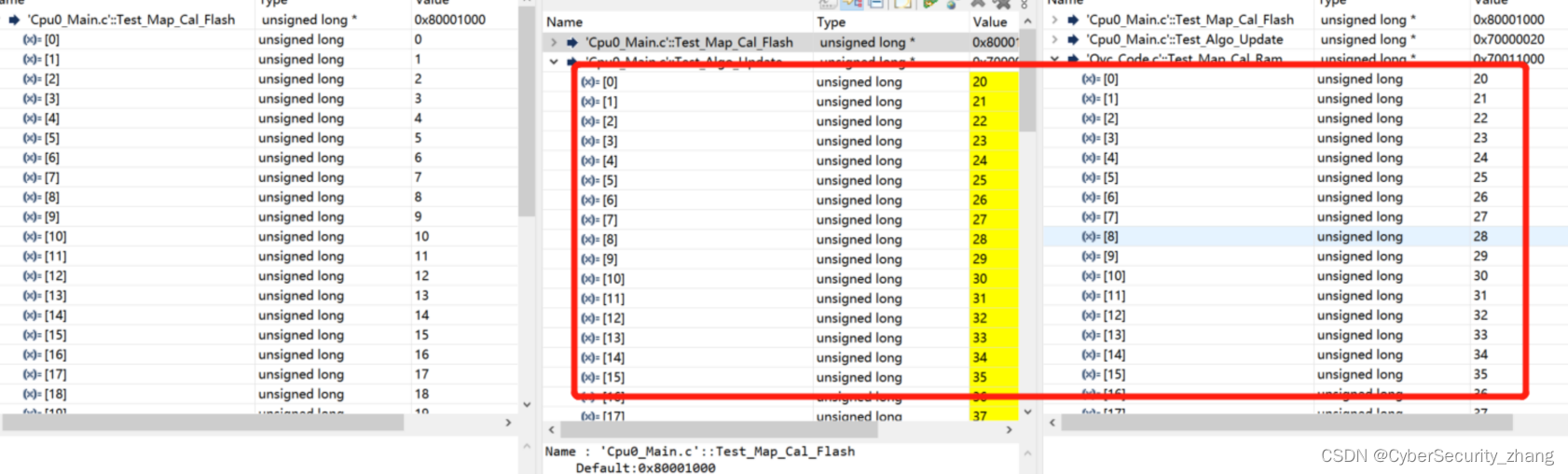
英飞凌TC3xx-Overlay
目录 1.数据访问重定向 2.寄存器说明 3.Overlay功能配置 3.1 确认用于重定向的CPU 3.2 配置重定向Block大小 3.3 配置目标地址和重定向地址 4.结果验证 5.小结 今天说要开个专栏讲讲XCP标定,但在将标定之前,先把英飞凌专门为标定功能设计overlay…...

Win10系统有几种复制文件的命令,哪种最强大?
环境: Win10 专业版 问题描述: Win10系统有几种复制文件的命令,哪种最强大? 解决方案: 在 Windows 10 中,复制文件的命令有以下几种: 使用 xcopy 命令:xcopy 是一个功能强大的…...

力扣202.快乐数
原题链接:202.快乐数 要记住的就是,需要判断元素是否出现过,或者是否在集合里存在,就可以考虑用哈希法去做 因为是每一位都进行平方后相加得到新的数,所以需要单独写一个函数进行每位相加的运算得到最终的sum 不断重…...
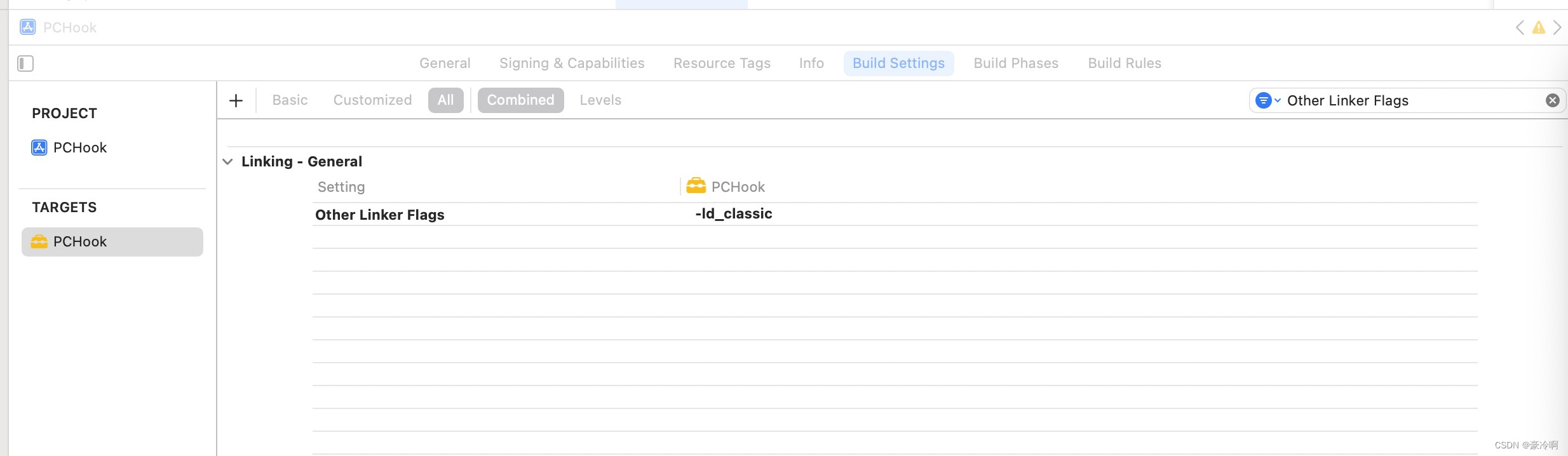
iOS Xcode15 适配:Other Linker Flags:-ld_classic
0x00 适配是一条没有尽头的路 Xcode 14 毛问题都没有,Xcode 15 崩溃 看图说话 0x01 解决方案 Other Linker Flags 添加 -ld_classic 即可 0x02 我的小作品 欢迎体验我的作品之一:小挑战-XGame 拼图游戏,渐变色游戏,经典24点游…...
)
springboot苍穹外卖实战:六、redis(Spring Data Redis)
Spring Data Redis 简介 网址:https://spring.io/projects/spring-data-redis Spring Data Redis中提供了一个高度封装的类:RedisTemplate,对相关api进行了归类封装,将同一类型操作封装为operation接口,具体分类如下࿱…...
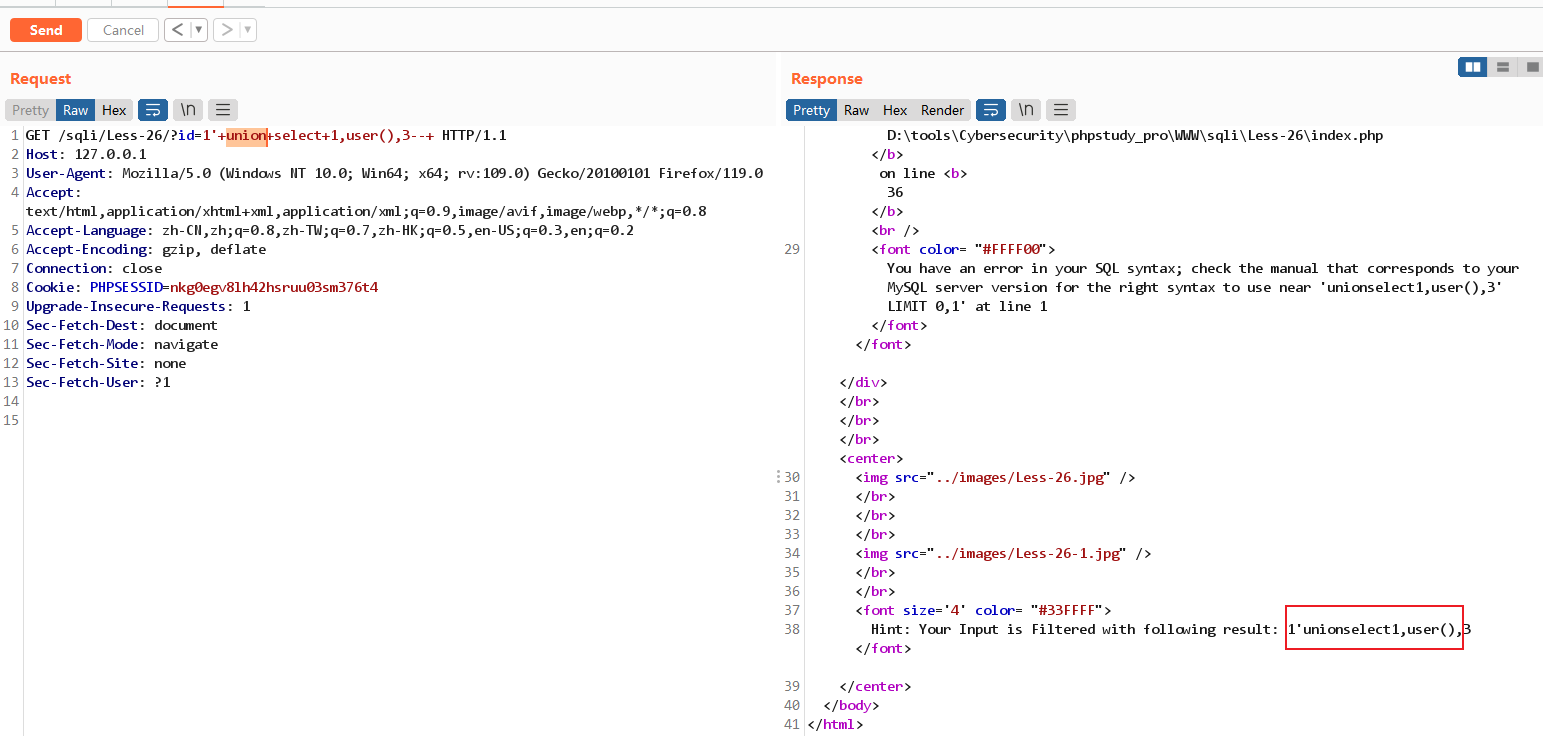
sqli 靶场 Level23-Level30 wp
level-23 (注释被过滤) 抓包,查看正常请求和响应。 略 尝试是否存在注入 id1’,id1’,成周期性变化 尝试 POC POC: id1andextractValue(1,concat(0x7e,user()))-- 结果:failed。怀疑–被过滤掉了,尝试…...

《完蛋!我被美女包围了》突然火了!世界首个开源贡献榜出炉丨 RTE 开发者日报 Vol.75
开发者朋友们大家好: 这里是 「RTE 开发者日报」 ,每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE (Real Time Engagement) 领域内「有话题的 新闻 」、「有态度的 观点 」、「有意思的 数据 」、「有思考的 文…...

C++ Qt 学习(一):Qt 入门
Qt6 安装教程 0. 基础知识 0.1 qmake 和 cmake 对比 qmake:qt 独有的代码构建工具cmake:C 通用的代码构建工具,绝大部分 C 开源项目都使用 cmake 管理代码qt 项目,没有特殊要求,使用 qmake 即可 0.2 Qt 3 个窗口类的…...

高性能消息中间件 - Kafka3.x(三)
文章目录 高性能消息中间件 - Kafka3.x(三)Kafka Broker ⭐Kafka Broker概念Zookeeper(新版本可以不使用zk了)⭐Zookeeper的作用 Kafka的选举1:Broker选举Leader⭐Broker核心参数⭐案例:服役新节点和退役旧…...

【八】Linux成神之路
Linux成神之路 简介:最近梳理了一下自己linux系统的学习历程,感觉整个成长过程就很顺利,并没有走弯路,于是想着可以不可以把自己linux系统学习的路线记录下来,能够在大家成长的路上有一点帮助,就在这样的一…...

功能测试用例,需要详细到什么程度?
📢专注于分享软件测试干货内容,欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢交流讨论:欢迎加入我们一起学习!📢资源分享:耗时200小时精选的「软件测试」资…...
VScode远程连接错误:进程试图写入不存在的管道
使用VScode连接树莓派时,出现远程连接错误:进程试图写入不存在的管道 解决方案: (1)可以进入config所在文件夹,删除文件 (2)无法解决的化尝试下述方法 输入 Remotting-SSH:Settin…...
Python测试之Pytest详解
概要 当涉及到python的测试框架时,pytest是一个功能强大且广泛应用的第三方库。它提供简洁而灵活的方式来编写和执行测试用例,并具有广泛的应用场景。下面是pytest的介绍和详细使用说明: pytest是一个用于python单元测试的框架,它…...
uni-app微信小程序打开第三方地图
需求 小程序中有个按钮点击以后会调用手机中第三方地图进行导航。参数 位置信息 经度 与纬度。 实现方法 uni.openLocation({latitude: Number(地址纬度),longitude: Number(地址经度),name: 地址名称,address: 地址详情,success: function (res) {console.log(打开系统位置地…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
