AM@微分方程相关概念@线性微分方程@一阶线性微分方程的通解
文章目录
- abstract
- 引言
- 一般的微分方程
- 常微分方程
- 微分方程的解
- 隐式解
- 通解和特解
- 初始条件
- 初值问题
- 微分方程的积分曲线
- 线性微分方程
- 一阶线性微分方程
- 一阶齐次和非齐次线性微分方程
- 一阶齐次线性微分方程的解
- 一阶非齐次线性微分方程的解
abstract
- AM@微分方程相关概念@线性微分方程@一阶线性微分方程的通解
引言
- 经验表明,获得微分方程的一般性数学理论是困难的
- 有少数类型的微分方程,比如线性微分方程具有一般的求解理论
- 还有一些一阶的简单的微分方程类型
一般的微分方程
-
含有未知函数,未知函数的导数与自变量之间的关系的方程,称为微分方程;
-
未知函数导数的最高阶数称为该微分方程的阶
-
方程 F ( x , y , y ′ , ⋯ , y n ) = 0 F(x,y,y',\cdots,y^{n})=0 F(x,y,y′,⋯,yn)=0
(1)或方程 y ( n ) y^{(n)} y(n)= f ( x , y , y ′ , ⋯ , y ( n − 1 ) ) f(x,y,y',\cdots,y^{(n-1)}) f(x,y,y′,⋯,y(n−1))(1-1)成为 n n n阶微分方程(形式(1-1)是一种常见的微分方程形式) -
其中 x , y , y ′ ⋯ , y ( n − 1 ) x,y,y'\cdots,y^{(n-1)} x,y,y′⋯,y(n−1)可以没有,但必须有最高阶导数 y ( n ) y^{(n)} y(n)
-
当 n = 1 n=1 n=1时,方程(1)称为一阶微分方程
-
常微分方程
- 未知函数是一元函数的微分方程称为常微分方程
微分方程的解
- 设 y = ϕ ( x ) y=\phi(x) y=ϕ(x)在区间 I = ( a , b ) I=(a,b) I=(a,b)上连续且 n n n阶可导,使得 F ( x , ϕ ( x ) , ϕ ′ ( x ) , ⋯ , ϕ ( n ) ( x ) ) = 0 F(x,\phi(x),\phi'(x),\cdots,\phi^{(n)}(x))=0 F(x,ϕ(x),ϕ′(x),⋯,ϕ(n)(x))=0,
(2)即式(1)恒成立,则称 y = ϕ ( x ) y=\phi(x) y=ϕ(x)为该微分方程在区间 I I I上的一个解
隐式解
- 若关系 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0
(3)确定的隐函数 y = ϕ ( x ) y=\phi(x) y=ϕ(x)是(1)的解,则称(3)是(1)的隐式解 - 例如: x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1
(4)是一阶微分方程 y ′ = − x y y'=-\frac{x}{y} y′=−yx(4-1)的隐式解- 对(4)求导, 2 x + 2 y y ′ = 0 2x+2yy'=0 2x+2yy′=0,变形得(4-1)式
通解和特解
- 若含有 n n n个独立任意常数的函数 y = ϕ ( x , C 1 , ⋯ , C n ) y=\phi(x,C_1,\cdots,C_n) y=ϕ(x,C1,⋯,Cn), x ∈ I x\in{I} x∈I
(5)是 n n n阶微分方程(1)的解,则称(5)是(1)的通解 - 不含任意常数的解称为特解
- 详见函数线性相关性
初始条件
- 关系式: y ( i ) ( x 0 ) = y 0 ( i ) y^{(i)}(x_0)=y_0^{(i)} y(i)(x0)=y0(i), ( i = 0 , 1 , 2 , ⋯ , n ) (i=0,1,2,\cdots,n) (i=0,1,2,⋯,n)称为 n n n阶微分方程的初始条件
- 其中 y 0 i y_{0}^{i} y0i, ( i = 0 , 1 , 2 , ⋯ , n ) (i=0,1,2,\cdots,n) (i=0,1,2,⋯,n)为 n n n个给定的数
初值问题
-
一般地,由初始条件确定通解中的任意常数,就得到相应的一个特解
-
上述方式确定特解的问题称为初值问题
-
利用初始条件定义特解:微分方程中,满足初始条件的解称为特解
微分方程的积分曲线
- 微分方程的解(函数)的图形是一条曲线,称为微分方程的积分曲线
- 一阶微分方程的初值问题
- y ′ = f ( x , y ) y'=f(x,y) y′=f(x,y); y ′ ∣ x = x 0 = y 0 y'|_{x=x_0}=y_0 y′∣x=x0=y0的几何意义,就是求通过点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的那条积分曲线
线性微分方程
-
方程 ∑ i = 0 n a i ( x ) y ( i ) \sum_{i=0}^{n}a_{i}(x)y^{(i)} ∑i=0nai(x)y(i)= f ( x ) f(x) f(x),
(1);式(1)展开写为: y ( n ) + a 1 ( x ) y ( n − 1 ) + ⋯ + a n − 1 ( x ) y ′ + a n ( x ) y y^{(n)}+a_1(x)y^{(n-1)}+\cdots+a_{n-1}(x)y^{'}+a_n(x)y y(n)+a1(x)y(n−1)+⋯+an−1(x)y′+an(x)y= f ( x ) f(x) f(x);该方程称为** n n n阶线性微分方程** -
若式(1)中 f ( x ) = 0 f(x)=0 f(x)=0,此时方程(1)作 ∑ i = 1 n a i ( x ) y ( i ) = 0 \sum_{i=1}^{n}a_{i}(x)y^{(i)}=0 ∑i=1nai(x)y(i)=0
(2),称为** n n n阶线性齐次微分方程**,并且称(2)是(1)对应的齐次方程 -
若式(1)中 f ( x ) ≠ 0 f(x)\neq{0} f(x)=0,其中系数 a i ( x ) a_i(x) ai(x)是已知函数,并假设 a i ( x ) a_i(x) ai(x), f ( x ) f(x) f(x)在某个区间 ( a , b ) (a,b) (a,b)内连续,则式(1)为** n n n阶线性非齐次微分方程**, f ( x ) f(x) f(x)称为自由项
一阶线性微分方程
-
形如 d y d x + P ( x ) y = Q ( x ) \frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x) dxdy+P(x)y=Q(x)
(1)的方程称为一阶线性微分方程 -
其通解为
-
y = C e − ∫ P ( x ) d x + e − ∫ P ( x ) d x ⋅ ∫ Q ( x ) e ∫ P ( x ) d x d x y=Ce^{-\int{P(x)}\mathrm{d}x}+{e^{-\int{P(x)}\mathrm{d}x}}\cdot\int{Q(x)e^{\int{P(x)\mathrm{d}x}}\mathrm{d}x} y=Ce−∫P(x)dx+e−∫P(x)dx⋅∫Q(x)e∫P(x)dxdx
-
另一种表示方式: y = exp ( − ∫ P ( x ) d x ) ( ∫ [ Q ( x ) exp ( ∫ P ( x ) d x ) d x ] + C ) y=\exp\left(-\int{P(x)\mathrm{d}x}\right) \left(\int{[Q(x)}\exp\left(\int{P(x)\;\mathrm{d}x}\right)\;\mathrm{d}x]+C \right) y=exp(−∫P(x)dx)(∫[Q(x)exp(∫P(x)dx)dx]+C)
-
一阶齐次和非齐次线性微分方程
- 若 Q ( x ) ≡ 0 Q(x)\equiv{0} Q(x)≡0,则称 d y d x + P ( x ) y = 0 \frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=0 dxdy+P(x)y=0
(2)为对应于(1)的齐次线性方程 - 若 Q ( x ) ≢ 0 Q(x)\not\equiv{0} Q(x)≡0(函数 Q ( x ) Q(x) Q(x)不总是取 0 0 0,这不同于函数 Q ( x ) ≠ 0 Q(x)\neq{0} Q(x)=0(不取0)),则称 d y d x + P ( x ) y = Q ( x ) ≢ 0 \frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)\not\equiv{0} dxdy+P(x)y=Q(x)≡0
(3)为非齐次线性方程
一阶齐次线性微分方程的解
- 方程(2)是可分离变量的: d y y \frac{\mathrm{d}y}{y} ydy= − P ( x ) d x -P(x)\mathrm{d}x −P(x)dx
(4),两边积分,得 ln ∣ y ∣ \ln|y| ln∣y∣= − ∫ P ( x ) d x + C 1 -\int{P(x)\mathrm{d}x}+C_1 −∫P(x)dx+C1(4-1) - 两边取指数: ∣ y ∣ |y| ∣y∣= e − ∫ P ( x ) d x + C 1 e^{-\int{P(x)\mathrm{d}x}+C_1} e−∫P(x)dx+C1= e − ∫ P ( x ) d x ⋅ e C 1 e^{-\int{P(x)\mathrm{d}x}}\cdot{e^{C_1}} e−∫P(x)dx⋅eC1
(5),为了便于书写复杂指数,使用 exp x \exp{x} expx表示 e x e^{x} ex,则式(5)可以表示为 ∣ y ∣ |y| ∣y∣= exp ( − ∫ P ( x ) d x + C 1 ) \exp{(-\int{P(x)}\mathrm{d}x+C_1)} exp(−∫P(x)dx+C1)= exp ( C 1 ) ⋅ exp ( − ∫ P ( x ) d x ) \exp(C_1)\cdot\exp{(-\int{P(x)}\mathrm{d}x)} exp(C1)⋅exp(−∫P(x)dx) - y = ± exp ( C 1 ) ⋅ exp ( − ∫ P ( x ) d x ) y=\pm{\exp(C_1)\cdot\exp{(-\int{P(x)}\mathrm{d}x)}} y=±exp(C1)⋅exp(−∫P(x)dx)= C exp ( − ∫ P ( x ) d x ) C\exp{(-\int{P(x)}\mathrm{d}x)} Cexp(−∫P(x)dx)
(6),其中 C = ± exp ( C 1 ) C=\pm{\exp(C_1)} C=±exp(C1) - 式(6)就是方程(3)的通解
一阶非齐次线性微分方程的解
- 显然方程(2)是方程(1)的特殊情况,两者存在一定的联系
- 对方程(3)进行变形: d y y \mathrm{d}y\over{y} ydy= ( − P ( x ) + 1 y Q ( x ) ) d x (-P(x)+\frac{1}{y}Q(x))\mathrm{d}x (−P(x)+y1Q(x))dx
(7),两边积分 ln ∣ y ∣ \ln|y| ln∣y∣= ∫ ( − P ( x ) + 1 y Q ( x ) ) d x + C 1 \int{(-P(x)+\frac{1}{y}Q(x))\mathrm{d}x}+C_1 ∫(−P(x)+y1Q(x))dx+C1= ∫ ( − P ( x ) + 1 y Q ( x ) ) d x + ln ∣ C ∣ \int{(-P(x)+\frac{1}{y}Q(x))\mathrm{d}x}+\ln{|C|} ∫(−P(x)+y1Q(x))dx+ln∣C∣(7-1),其中 C 1 = ln ∣ C ∣ C_1=\ln{|C|} C1=ln∣C∣, C 1 C_1 C1可以取任何常数,但为了得到 y y y,我们要对(7-1)两边取指数, exp ln ∣ C ∣ \exp{\ln|C|} expln∣C∣= ∣ C ∣ |C| ∣C∣,是一个简单的值,继续展开(7-1), − ∫ P ( x ) d x + ∫ 1 y Q ( x ) d x + ln ∣ C ∣ -\int{P(x)}\mathrm{d}x+\int{\frac{1}{y}Q(x)\mathrm{d}x}+\ln{|C|} −∫P(x)dx+∫y1Q(x)dx+ln∣C∣(7-2) - 取指数, ∣ y ∣ |y| ∣y∣= exp ( − ∫ P ( x ) d x + ∫ 1 y Q ( x ) d x + ln ∣ C ∣ ) \exp{(-\int{P(x)}\mathrm{d}x+\int{\frac{1}{y}Q(x)\mathrm{d}x}+\ln{|C|})} exp(−∫P(x)dx+∫y1Q(x)dx+ln∣C∣)
(8),即 y = ± ∣ C ∣ exp ( − ∫ P ( x ) d x ) exp ( ∫ 1 y Q ( x ) d x ) y=\pm{|C|\exp(-\int{P(x)\mathrm{d}x})}\exp{(\int{\frac{1}{y}Q(x)\mathrm{d}x})} y=±∣C∣exp(−∫P(x)dx)exp(∫y1Q(x)dx)= C exp ( − ∫ P ( x ) d x ) exp ( ∫ 1 y Q ( x ) d x ) C{\exp(-\int{P(x)\mathrm{d}x})}\exp{(\int{\frac{1}{y}Q(x)\mathrm{d}x})} Cexp(−∫P(x)dx)exp(∫y1Q(x)dx)(9)- 其中 C = ± ∣ C ∣ C=\pm{|C|} C=±∣C∣
- C exp ( − ∫ P ( x ) d x ) C{\exp(-\int{P(x)\mathrm{d}x})} Cexp(−∫P(x)dx),这就是式(6),即式(9)包含一阶齐次线性微分方程的通解
- 记 T = exp ( ∫ 1 y Q ( x ) d x ) T=\exp{(\int{\frac{1}{y}Q(x)\mathrm{d}x})} T=exp(∫y1Q(x)dx)
- 其中 C = ± ∣ C ∣ C=\pm{|C|} C=±∣C∣
- T T T是关于 x x x的函数( y y y是关于 x x x的一元函数,所以 T T T是 x x x的函数,可以表示为 T ( x ) T(x) T(x)),
- 式(9)也是关于 x x x的函数,但其表达式包含 y y y,下面的工作是化去式等号右边的 y y y,使之仅含有已知的关于 x x x的函数式
- 因此,比较式(9),(6),利用常数变易法,将方程(6)中的 C C C变易为 x x x的待定函数 C ( x ) C(x) C(x),使之满足方程(1),从而求出 C ( x ) C(x) C(x)(其表示的是 C T ( x ) CT(x) CT(x)
- 令 y = C ( x ) exp ( − ∫ P ( x ) d x ) y=C(x)\exp{(-\int{P(x)}\mathrm{d}x)} y=C(x)exp(−∫P(x)dx);
(10),对其两边求导 - d y d x \frac{\mathrm{d}y}{\mathrm{d}x} dxdy= C ′ ( x ) exp ( − ∫ P ( x ) d x ) C'(x)\exp{(-\int{P(x)}\mathrm{d}x)} C′(x)exp(−∫P(x)dx)+ C ( x ) exp ( − ∫ P ( x ) d x ) ( − P ( x ) ) C(x)\exp{(-\int{P(x)}\mathrm{d}x)}(-P(x)) C(x)exp(−∫P(x)dx)(−P(x))
- = C ′ ( x ) exp ( − ∫ P ( x ) d x ) C'(x)\exp{(-\int{P(x)}\mathrm{d}x)} C′(x)exp(−∫P(x)dx)- C ( x ) P ( x ) exp ( − ∫ P ( x ) d x ) ) C(x)P(x)\exp{(-\int{P(x)}\mathrm{d}x)}) C(x)P(x)exp(−∫P(x)dx))
(11)
- = C ′ ( x ) exp ( − ∫ P ( x ) d x ) C'(x)\exp{(-\int{P(x)}\mathrm{d}x)} C′(x)exp(−∫P(x)dx)- C ( x ) P ( x ) exp ( − ∫ P ( x ) d x ) ) C(x)P(x)\exp{(-\int{P(x)}\mathrm{d}x)}) C(x)P(x)exp(−∫P(x)dx))
- 将(10),(11)代入方程(1),得 C ′ ( x ) exp ( − ∫ P ( x ) d x ) C'(x)\exp{(-\int{P(x)}\mathrm{d}x)} C′(x)exp(−∫P(x)dx)- C ( x ) P ( x ) exp ( − ∫ P ( x ) d x ) ) C(x)P(x)\exp{(-\int{P(x)}\mathrm{d}x)}) C(x)P(x)exp(−∫P(x)dx))+ P ( x ) C ( x ) exp ( − ∫ P ( x ) d x ) P(x)C(x)\exp{(-\int{P(x)}\mathrm{d}x)} P(x)C(x)exp(−∫P(x)dx)= Q ( x ) Q(x) Q(x);
- 即得 C ′ ( x ) exp ( − ∫ P ( x ) d x ) C'(x)\exp{(-\int{P(x)}\mathrm{d}x)} C′(x)exp(−∫P(x)dx)= Q ( x ) Q(x) Q(x),
(11-1),整理可得 C ′ ( x ) C'(x) C′(x)= Q ( x ) exp ( ∫ ( P ( x ) d x ) ) Q(x)\exp{(\int(P(x)\mathrm{d}x))} Q(x)exp(∫(P(x)dx))(11-2),两边积分,就求得函数 C ( x ) C(x) C(x)= ∫ [ Q ( x ) exp ( ∫ ( P ( x ) d x ) ) ] d x + C \int{[Q(x)\exp{(\int(P(x)\mathrm{d}x))}]\mathrm{d}x}+C ∫[Q(x)exp(∫(P(x)dx))]dx+C(12) - 将式(12)代入到(10),得方程(3)的通解: y = [ ∫ [ Q ( x ) exp ( ∫ ( P ( x ) d x ) ) ] d x + C ] y=[\int{[Q(x)\exp{(\int(P(x)\mathrm{d}x))}]\mathrm{d}x} +C] y=[∫[Q(x)exp(∫(P(x)dx))]dx+C] ⋅ \cdot ⋅ [ exp ( − ∫ P ( x ) d x ) ] [\exp{(-\int{P(x)}\mathrm{d}x)]} [exp(−∫P(x)dx)]
(13),习惯上把指数式放在前面,即 y y y= [ exp ( − ∫ P ( x ) d x ) ] [\exp{(-\int{P(x)}\mathrm{d}x)]} [exp(−∫P(x)dx)] ⋅ \cdot ⋅ [ ∫ [ Q ( x ) exp ( ∫ ( P ( x ) d x ) ) ] d x + C ] [\int{[Q(x)\exp{(\int(P(x)\mathrm{d}x))}]\mathrm{d}x} +C] [∫[Q(x)exp(∫(P(x)dx))]dx+C](13-1),或者展开成两项和:- y y y= C [ exp ( − ∫ P ( x ) d x ) ] C[\exp{(-\int{P(x)}\mathrm{d}x)]} C[exp(−∫P(x)dx)]+ [ exp ( − ∫ P ( x ) d x ) ] [\exp{(-\int{P(x)}\mathrm{d}x)]} [exp(−∫P(x)dx)] [ ∫ [ Q ( x ) exp ( ∫ ( P ( x ) d x ) ) ] d x ] [\int{[Q(x)\exp{(\int(P(x)\mathrm{d}x))}]\mathrm{d}x}] [∫[Q(x)exp(∫(P(x)dx))]dx]
(14) - 式(14)中第一项(包含任意常数)就是齐次方程(2)的解,第二项(不包含任意常数)是非齐次方程(3)的一个特解
- y y y= C [ exp ( − ∫ P ( x ) d x ) ] C[\exp{(-\int{P(x)}\mathrm{d}x)]} C[exp(−∫P(x)dx)]+ [ exp ( − ∫ P ( x ) d x ) ] [\exp{(-\int{P(x)}\mathrm{d}x)]} [exp(−∫P(x)dx)] [ ∫ [ Q ( x ) exp ( ∫ ( P ( x ) d x ) ) ] d x ] [\int{[Q(x)\exp{(\int(P(x)\mathrm{d}x))}]\mathrm{d}x}] [∫[Q(x)exp(∫(P(x)dx))]dx]
- 总之,一阶非齐次线性微分方程的通解等于对应的齐次方程的通解加上非齐次方程的一个特解之和;这一点和线性代数中非齐次线性方程组解的结构结论相仿
- 令 y = C ( x ) exp ( − ∫ P ( x ) d x ) y=C(x)\exp{(-\int{P(x)}\mathrm{d}x)} y=C(x)exp(−∫P(x)dx);
相关文章:

AM@微分方程相关概念@线性微分方程@一阶线性微分方程的通解
文章目录 abstract引言 一般的微分方程常微分方程微分方程的解隐式解通解和特解初始条件初值问题微分方程的积分曲线 线性微分方程一阶线性微分方程一阶齐次和非齐次线性微分方程一阶齐次线性微分方程的解一阶非齐次线性微分方程的解 abstract AM微分方程相关概念线性微分方程…...

基于深度学习的安全帽识别检测系统(python OpenCV yolov5)
收藏和点赞,您的关注是我创作的动力 文章目录 概要 一、研究的内容与方法二、基于深度学习的安全帽识别算法2.1 深度学习2.2 算法流程2.3 目标检测算法2.3.1 Faster R-CNN2.3.2 SSD2.3.3 YOLO v3 三 实验与结果分析3.1 实验数据集3.1.1 实验数据集的构建3.1.2 数据…...
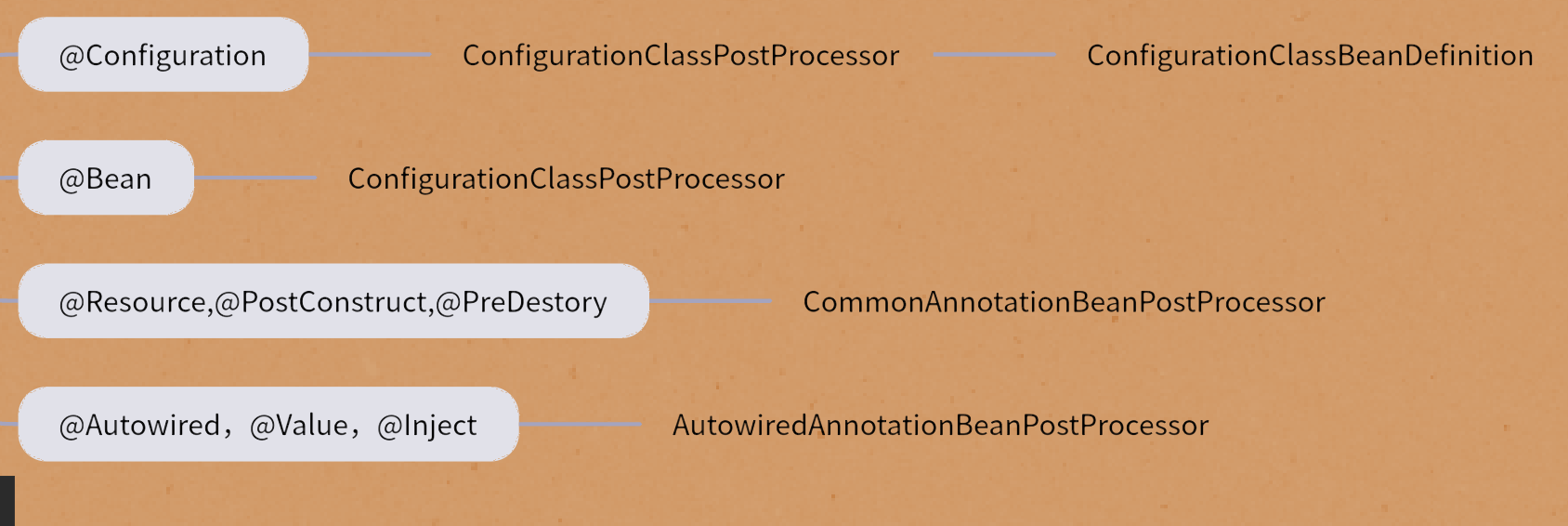
Spring源码分析篇一 @Autowired 是怎样完成注入的?究竟是byType还是byName亦两者皆有
1. 五种不同场景下 Autowired 的使用 第一种情况 上下文中只有一个同类型的bean 配置类 package org.example.bean;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration;Configuration public class FruitCo…...

Goby 漏洞发布|F5 BIG-IP AJP 身份认证绕过漏洞(CVE-2023-46747)
漏洞名称:F5 BIG-IP AJP 身份认证绕过漏洞(CVE-2023-46747) English Name:F5 BIG-IP AJP authentication bypass vulnerability (CVE-2023-46747) CVSS core: 10 影响资产数: 307282 漏洞描述: Cisco …...

Vue中watch侦听器用法
watch 需要侦听特定的数据源,并在单独的回调函数中执行副作用 watch第一个参数监听源 watch第二个参数回调函数cb(newVal,oldVal) watch第三个参数一个options配置项是一个对象{ immediate:true //是否立即调用一次 deep:true //是否开启…...

[算法前沿]--054-大语言模型的学习材料
大语言模型的学习材料 Other Papers If you’re interested in the field of LLM, you may find the above list of milestone papers helpful to explore its history and state-of-the-art. However, each direction of LLM offers a unique set of insights and contribut…...

DWA算法,仿真转为C用于无人机避障
DWA算法,仿真转为C用于无人机避障 链接: 机器人局部避障的动态窗口法(dynamic window approach) 链接: 机器人局部避障的动态窗口法DWA (dynamic window approach)仿真源码详细注释版 链接: 常见路径规划算法代码-Matlab (纯代码篇) …...

现阶段的主流数据库分别是哪几种?
关系型数据库 1. MySQL数据库 MySQL是最受欢迎的开源SQL数据库管理系统,它由 MySQL AB开发、发布和支持。MySQL AB是一家基于MySQL开发人员的商业公司,它是一家使用了一种成功的商业模式来结合开源价值和方法论的第二代开源公司。MySQL是MySQL AB的注册商…...
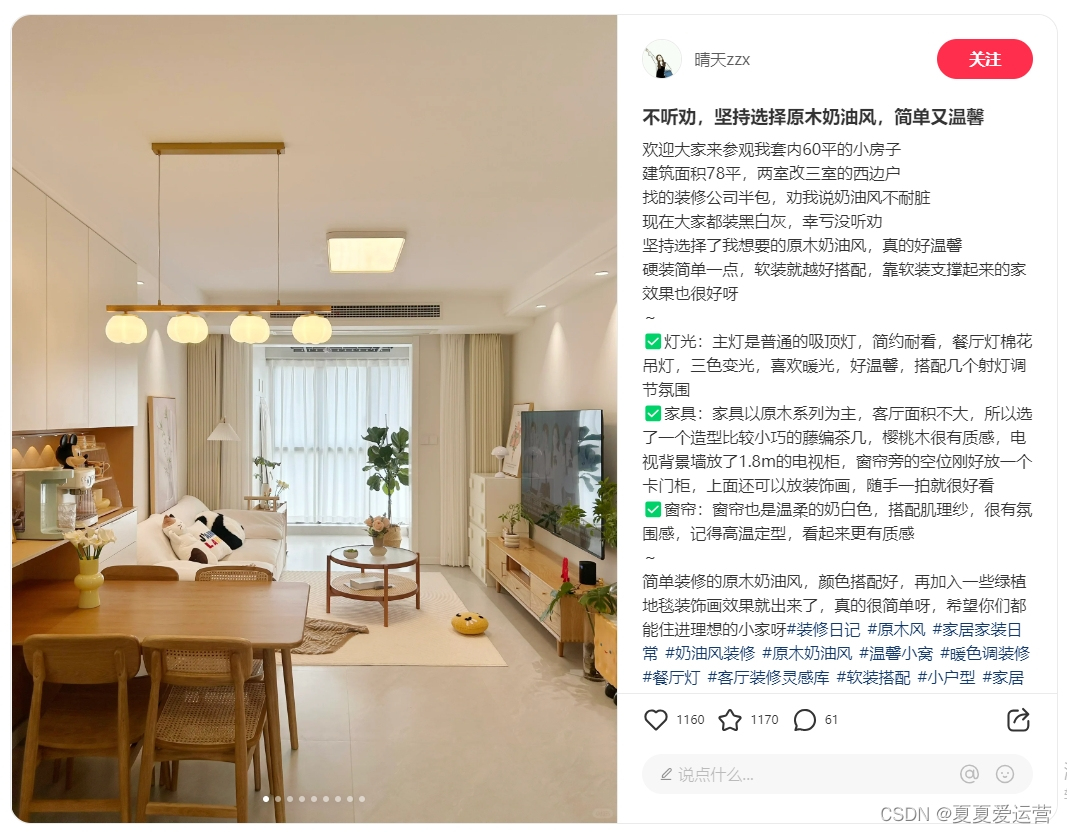
“原生感”暴涨311%,这届年轻人不再爱浓妆?丨小红书数据分析
近年来,越来越多美妆博主在社交媒体平台安利“原生感妆容”,即我们所熟知的“伪素颜妆”、“裸妆”、“白开水妆”,显然,追求“原生感”成为当代妆容主流。通过小红书数据分析工具,查看#原生感妆容 话题,近…...
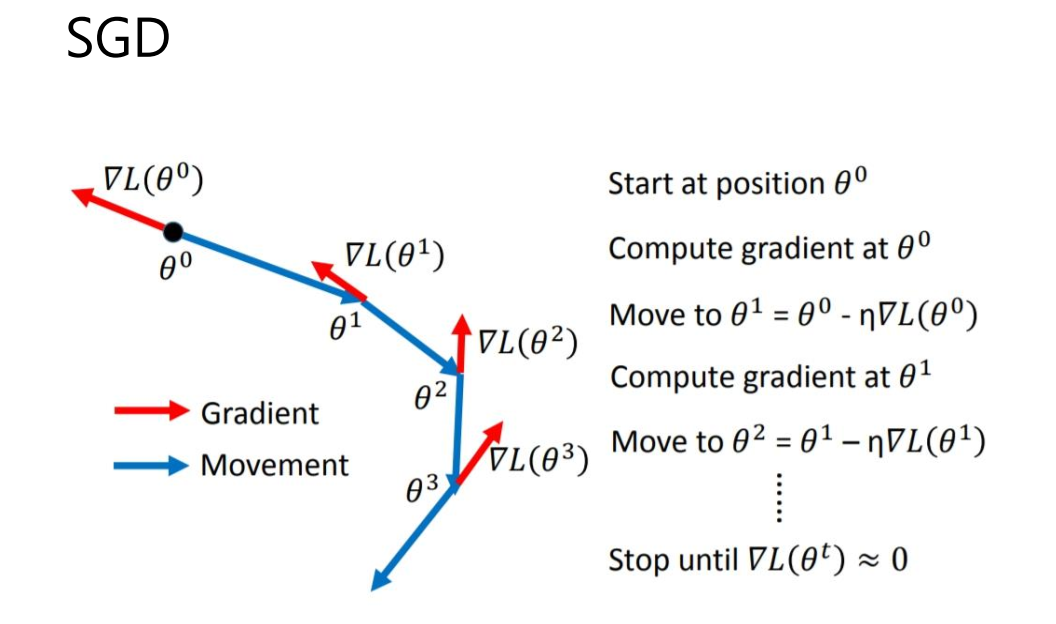
基于深度学习的植物识别算法 - cnn opencv python 计算机竞赛
文章目录 0 前言1 课题背景2 具体实现3 数据收集和处理3 MobileNetV2网络4 损失函数softmax 交叉熵4.1 softmax函数4.2 交叉熵损失函数 5 优化器SGD6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习的植物识别算法 ** …...
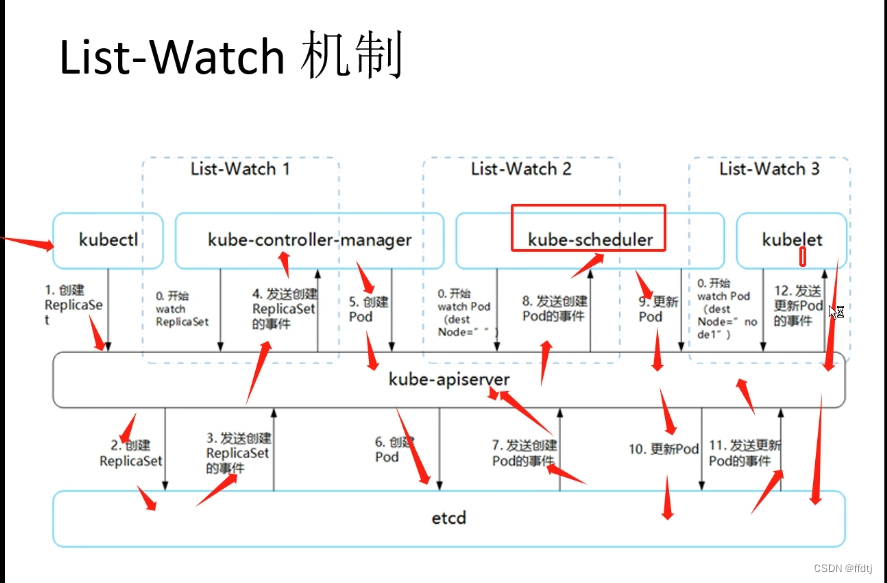
k8s调度约束
List-Watch Kubernetes 是通过 List-Watch的机制进行每个组件的协作,保持数据同步的,每个组件之间的设计实现了解耦。 List-Watch机制 工作机制:用户通过 kubectl请求给 APIServer 来建立一个 Pod。APIServer会将Pod相关元信息存入 etcd 中…...
面经(面试经验)第一步,从自我介绍开始说起
看到一位同学讲自己的面试步骤和过程,我心有所感,故此想整理下面试的准备工作。以便大家能顺利应对面试,通过面试... 求职应聘找工作,面试是必然的关卡,如今竞争激烈呀,想要得到自己喜欢的工作,…...
S/4 HANA 中的 Email Template
1 如何创建Email Template? 没有特定的事务用于创建电子邮件模板,我们可以将其创建为 SE80 事务中的存储库对象,如下所示: 1,选择包(或本地对象)并右键单击。 2,选择“创建”->“更多”->“电子邮件模板” 尽管如此,对于已有的Email Template,可以使用程序…...

\r\n和\n的区别 回车/换行 在不同系统下的区别
文章目录 1 \r\n和\n的区别2 什么是 回车/换行3 \r\n和\n 故事 1 \r\n和\n的区别 \r\n和\n是两个常见的控制字符符号,它们在计算机领域中有着不同的作用和用途。 \r\n在Windows系统中被广泛使用,而\n在Unix和Linux系统中更为常见。 在Windows操作系统中…...

机械应用笔记
1. 螺纹转换头:又名金属塞头,例如M20-M16;适合于大小螺纹转换用; 2. 螺纹分英制和公制,攻丝同样也有英制和公制之分; 3. DB9头制作,M6.5的线,用M6.5的钻头扩线孔,在根…...

机房精密空调发生内部设备通信故障不一会压缩机就停止工作,怎么处理?
环境: 山特AT-DA810U 精密空调 问题描述: 机房精密空调发生内部设备通信故障不一会压缩机就停止工作,怎么处理? 回风处不显示温湿度 解决方案: 1.进入诊断模式工程师密码333333 看到压缩机关闭了,强制输出测试一下压缩机正常 2.尝试更换温湿度传感器模块网口,重启…...

手机端运维管理系统——图扑 HT for Web
随着信息技术的快速发展,网络技术的应用涉及到人们生活的方方面面。其中,手机运维管理系统可提供数字化、智能化的方式,帮助企业和组织管理监控企业的 IT 环境,提高运维效率、降低维护成本、增强安全性、提升服务质量,…...

中期科技:智慧公厕打造智能化城市设施,提升公共厕所管理与服务体验
智慧公厕是利用先进的技术和创新的解决方案来改进公厕的设施和管理。借助物联网、互联网、5G/4G通信、人工智能、大数据、云计算等新兴技术的集成,智慧公厕具备了一系列令人惊叹的应用功能。从监测公厕内部人体活动状态、人体存在状态,到空气质量情况、环…...

innovus: set_ccopt_property的基本用法
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 clock route clock route的net type分为三种,分别是root、trunk和leaf,其中root是指fanout超过routing_top_fanout_count约束的net,leaf是指…...

打造美团外卖新体验,HarmonyOS SDK持续赋能开发者共赢鸿蒙生态
从今年8月起,所有升级到HarmonyOS 4的手机用户在美团外卖下单后,可通过屏幕上的一个“小窗口”,随时追踪到“出餐、取餐、送达”等订单状态。这个能让用户实时获悉订单进度的神奇“小窗口”,就是实况窗功能。 实况窗:简…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
