【力扣】2127. (分类讨论 + 拓扑排序)参加会议的最多员工数
【力扣】2127. (分类讨论 + 拓扑排序)参加会议的最多员工数
文章目录
- 【力扣】2127. (分类讨论 + 拓扑排序)参加会议的最多员工数
- 1. 题目介绍
- 2. 思路(**分类讨论 + 拓扑排序**)
- 3. 解题代码
- 4. Danger
- 参考
1. 题目介绍
一个公司准备组织一场会议,邀请名单上有 n 位员工。公司准备了一张 圆形 的桌子,可以坐下 任意数目 的员工。
-
要求:员工编号为 0 到 n - 1 。每位员工都有一位 喜欢 的员工,每位员工当且仅当他被安排在喜欢员工的旁边,他才会参加会议。每位员工喜欢的员工 不会 是他自己。
-
给你一个下标从 0 开始的整数数组 favorite ,其中 favorite[i] 表示第 i 位员工喜欢的员工。
-
请你返回参加会议的 最多员工数目 。
示例:
- 1

- 2

- 3

提示:

2. 思路(分类讨论 + 拓扑排序)
首先需要简单了解一下 基环内向树。在了解了树的基础上来解释基环树——树加一条边使之成环(也就是说,在严格意义上来说,基环树并不是树,就像老婆饼没有老婆一样,基环树是个图)。首先它是一个有向图,它构成类似基环树的结构。
- 最重要的特点就是每个点都有且只有一个出度,并且环外的节点方向指向环内。

针对这道题,我们可以把每个员工看成图上的一个节点,如果员工 x 喜欢员工 y,就在从 x 对应的节点到 y 对应的节点连一条边,那么形成的图则是会由若干颗「基环内向树」组成,就是形如下图所示的结构:

原因如下:
- 我们从任意一个节点 x 开始在图上进行「游走」,由于每个员工只有一位喜欢的员工,因此每个节点在图上只会有一条出边,即「游走」的过程是唯一的。由于图上有 n 个节点,因此在 n+1 步以内,一定会走到一个重复的节点,那么在第一次经过该节点之后,到第二次经过该节点之前的所有节点,以及该节点本身,就组成了一个环,如上图的蓝色节点所示。
- 对于不在环上的节点,我们已经说明了从它们开始「游走」也一定会进入到环中。在到达环上的节点之前,它们不会重复经过节点(否则就有两个环了,我们可以证明一个连通分量中是不可能有两个环的:因为每个节点只有一条出边,因此如果有两个环并且它们连通,那么必然某个环上有一个点有两条出边,一条出边指向同一个环上的节点,另一条出边可以使得它到达另一个环,这就产生了矛盾),那么它们就形成了类似树的结构,如上图的绿色节点所示。
- 需要注意的是,一个单独的环也是「基环内向树」,它是一种特殊情况,即没有绿色的节点。
思路与算法:既然我们知道了图由若干颗「基环内向树」组成,那么我们只需要计算每一颗「基环内向树」的哪一部分可以被安排参加会议,就可以来接这道题目。
- 1)首先讨论特殊的情况,即一个单独的环(或若干个环),并且所有环的大小都 ≥3。可以发现,我们按照环上的顺序给对应的员工安排座位是满足要求的,因为对于每一个环上的员工,它喜欢的员工就在它的旁边。并且,我们必须安排环上的所有员工,因为如果有缺失,那么喜欢那位缺失了的员工的员工就无法满足要求了。
- 但如果我们已经安排了某一个环上的所有员工,剩余的环就没有办法安排了。这是因为已经安排的那个环是没有办法被「断开」的:断开的本质就是相邻位置员工的缺失。因此,我们可以得出一个重要的结论:
- 如果我们想安排大小 ≥3 的环,我们最多只能安排一个,并且环需要是完整的。
- 但如果我们已经安排了某一个环上的所有员工,剩余的环就没有办法安排了。这是因为已经安排的那个环是没有办法被「断开」的:断开的本质就是相邻位置员工的缺失。因此,我们可以得出一个重要的结论:
- 2)接下来是,形成的图是 环大小 ≥3 的「基环内向树」,如果我们安排了不在环上的节点,那么从该节点开始,我们需要不断安排当前节点喜欢的员工,这实际上就是「游走」的过程。
- 而当我们游走到环上并到达环上最后一个未经过的节点时,该节点的下一个节点(即喜欢的员工)已经被安排过,所以最后一个未经过的节点就无法被安排(因为下一个节点不是他的喜欢节点),不满足要求。因此,我们不能安排任何不在环上的节点,只能安排在环上的节点,就得出了另一个的结论:
- 所有环大小 ≥3 的「基环内向树」与一个大小相同(指环的部分)的环是等价的。
- 而当我们游走到环上并到达环上最后一个未经过的节点时,该节点的下一个节点(即喜欢的员工)已经被安排过,所以最后一个未经过的节点就无法被安排(因为下一个节点不是他的喜欢节点),不满足要求。因此,我们不能安排任何不在环上的节点,只能安排在环上的节点,就得出了另一个的结论:
- 3)最后,需要考虑大小 =2 的环或者「基环内向树」了。
- 这里的特殊之处在于,大小 =2 的环可以安排多个:因为环上的两个点是互相喜欢的,因此只需要它们相邻即可,而没有其它的要求。
- 而对于环大小 =2 的「基环内向树」,如果我们安排了不在环上的节点,那么游走完环上两个节点之后,同样是满足要求的,并且我们甚至可以继续延伸(反向「游走」),到另一个不在环上的节点为止。如下图所示,包含 X 的节点就是可以安排参加会议的节点。

- 并且同样地,对于每一棵环大小 =2 的「基环内向树」,我们都可以取出这样一条「双向游走」路径进行安排,它们之间不会影响。
综上所述,原问题的答案即为下面二者中的最大值:
- 最大的环的大小;
- 所有环大小 =2 的「基环内向树」上的最长的「双向游走」路径之和。
为了求解「基环内向树」上的最长的「双向游走」路径,我们可以使用拓扑排序 + 动态规划的方法。记 f[i] 表示到节点 i 为止的最长「游走」路径经过的节点个数,那么状态方程即为:

- 即我们考虑节点 i 的上一个节点 j,在图中必须有从 j 到 i 的一条有向边,这样我们就可以从 j 转移到 i。如果不存在满足要求的 j(例如「基环内向树」退化成一个大小 =2 的环),那么 f[i]=1。状态转移可以和拓扑排序同时进行。
- 在拓扑排序完成后,剩余没有被弹出过队列的节点就是环上的节点。我们可以找出每一个环。如果环的大小 ≥3,我们就用其来更新最大的环的大小;如果环的大小 =2,设环上的两个节点为 x 和 y,那么该「基环内向树」上最长的「双向游走」的路径长度就是 f[x]+f[y]。
时间复杂度:O(n)。图中有 n 个节点和 n 条边,拓扑排序需要的时间为 O(n),后续找出所有环的时间也为 O(n)。
空间复杂度:O(n)。我们需要若干个长度为 n 的数组。
3. 解题代码
class Solution:def maximumInvitations(self, favorite: List[int]) -> int:n = len(favorite)# 统计入度,便于进行拓扑排序indeg = [0] * nfor i in range(n):indeg[favorite[i]] += 1used = [False] * nf = [1] * nq = deque(i for i in range(n) if indeg[i] == 0)while q:u = q.popleft()used[u] = Truev = favorite[u]# 状态转移f[v] = max(f[v], f[u] + 1)indeg[v] -= 1if indeg[v] == 0:q.append(v)# ring 表示最大的环的大小# total 表示所有环大小为 2 的「基环内向树」上的最长的「双向游走」路径之和ring = total = 0for i in range(n):if not used[i]:j = favorite[i]# favorite[favorite[i]] = i 说明环的大小为 2if favorite[j] == i:total += f[i] + f[j]used[i] = used[j] = True# 否则环的大小至少为 3,我们需要找出环else:u = icnt = 0while True:cnt += 1u = favorite[u]used[u] = Trueif u == i:breakring = max(ring, cnt)return max(ring, total)
4. Danger
力扣(LeetCode)是领扣网络旗下专注于程序员技术成长和企业技术人才服务的品牌。源自美国硅谷,力扣为全球程序员提供了专业的IT技术职业化提升平台,有效帮助程序员实现快速进步和长期成长。此外,力扣(LeetCode)致力于解决程序员技术评估、培训、职业匹配的痛点,逐步引领互联网技术求职和招聘迈向专业化。
- 据了解到的情况,Easy题和Medium 题在面试中比较常见,通常会以手写代码之类的形式出现,您需要对问题进行分析并给出解答,并于面试官进行交流沟通,有时还会被要求分析时间复杂度8与空间复杂度°,面试官会通过您对题目的分析解答,了解您对常用算法的熟悉程度和您的程序实现功底。
- 而在一些对算法和程序实现功底要求较高的岗位,Hard 题也是很受到面试官的青睐,如果您在面试中成功Bug-Free出一道Hard题,我们相信您一定会给面试官留下很深刻的印象,并极大增加拿到Offer的概率,据相关人士统计,如果您在面试成功解出一道Hard题,拿不到Offer的概率无限接近于0。
- 所以,力扣中Easy和Medium相当于面试中的常规题,而Hard 则相当于面试中较难的题,解出—道Hard题,Offer可以说是囊中之物。
参考
【1】https://leetcode.cn/problems/maximum-employees-to-be-invited-to-a-meeting/?envType=daily-question&envId=2023-11-01
【2】https://leetcode.cn/problems/maximum-employees-to-be-invited-to-a-meeting/solutions/1190222/can-jia-hui-yi-de-zui-duo-yuan-gong-shu-u8e8u/
相关文章:

【力扣】2127. (分类讨论 + 拓扑排序)参加会议的最多员工数
【力扣】2127. (分类讨论 拓扑排序)参加会议的最多员工数 文章目录 【力扣】2127. (分类讨论 拓扑排序)参加会议的最多员工数1. 题目介绍2. 思路(**分类讨论 拓扑排序**)3. 解题代码4. Danger参考 1. 题…...
使用教程)
Flutter——最详细(Map)使用教程
Map简介 键值对的集合,您可以使用其关联的键从中检索值。 普通的 HashMap是无序的(不保证顺序),LinkedHashMap 按键插入顺序迭代,而像 SplayTreeMap 这样的排序映射按排序顺序迭代键。 1,添加元素 addEntri…...

vue的入门第一课
Vue.js是一款流行的JavaScript框架,用于构建交互式Web应用程序。本文将详细介绍Vue.js的基础知识,包括Vue.js的历史、设计模式、构造函数参数、el、data、computed、method、watch以及差值的使用。 Vue.js是什么? Vue.js是一款用于构建用户…...

已解决:conda找不到对应版本的cudnn如何解决?
1.解决方法 配置深度学习环境时,打算安装cudatoolkit11.2和cudnn8.1,当使用conda install cudnn8.0时,却搜索不到这个版本的包,解决方法如下: conda search cudnn -c conda-forge然后就可以使用如下命令进行安装对应…...

大语言模型的学习路线和开源模型的学习材料《二》
第三层 LLMs to Artifact 第一重 langchain 【LLMs 入门实战 —— 十二 】基于 本地知识库 的高效 🤖langchain-ChatGLM 介绍:langchain-ChatGLM是一个基于本地知识的问答机器人,使用者可以自由配置本地知识,用户问题的答案也是基于本地知识生成的。【LLMs 入门实战 ——…...

Flask-SQLAlchemy事件钩子介绍
一、前言 前几天在搜资料的时候无意中看到有介绍SQLAlchemy触发器,当时感觉挺奇怪的,触发器不是数据库层面的概念吗,怎么flask-SQLAlchemy这个ORM框架会有这玩意。 二、SQLAlchemy触发器一个简单例子 考虑到效率博客表中有两个字段…...

C++——list
目录 list介绍 list的函数接口 构造函数 push_front和pop_front push_back和pop_back insert erase 迭代器 front和back size resize empty clear list::sort unique reverse 迭代器的实现 list介绍 list是一种可以在常数范围内在任意位置进行插入和删除的序列…...

【Linux】第九站:make和makefile
文章目录 一、 Linux项目自动化构建工具make/Makefile1.make/makefile工作现象2.依赖关系与依赖方法3.如何清理4.为什么这里我们需要带上clean5.连续的make6.特殊符号 二、Linux下实现一个简单的进度条1.回车换行2.缓冲区3.倒计时的实现 一、 Linux项目自动化构建工具make/Make…...

一文了解什么是WebSocket
WebSocket 允许我们创建“实时”应用程序,与传统 API 协议相比,该应用程序速度更快且开销更少。 一、WebSocket 是如何工作的 按照传统的定义,WebSocket是一种双工协议,主要用于客户端-服务器通信通道。它本质上是双向的&…...

redis是什么
redis是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的API。和Memcached类似。redis支持存储的value类型相对更多,包括string(字符串)、list(链表)、set(集合)和zset(有序集合)。 一、 基本…...

基于深度学习的人脸专注度检测计算系统 - opencv python cnn 计算机竞赛
文章目录 1 前言2 相关技术2.1CNN简介2.2 人脸识别算法2.3专注检测原理2.4 OpenCV 3 功能介绍3.1人脸录入功能3.2 人脸识别3.3 人脸专注度检测3.4 识别记录 4 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于深度学习的人脸专注度…...

跨境电商的新引擎:崛起的网红经济
随着全球数字化时代的崛起,跨境电商成为了国际贸易的新引擎,而在这个巨大的变革浪潮中,网红经济正在崭露头角,成为这一引擎的有力推动者。在这篇文章中,我们将深入探讨网红经济如何催生跨境电商的新动力,以…...

P2006 赵神牛的游戏 python解法
赵神牛的游戏 题目描述 在 DNF 中,赵神牛有一个缔造者,他一共有 k k k 点法力值,一共有 m m m 个技能,每个技能耗费的法力值为 a i a_i ai,可以造成的伤害为 b i b_i bi,而 boss 的体力值为 n n…...

Unity的碰撞检测(六)
温馨提示:本文基于前一篇“Unity的碰撞检测(五)”继续探讨两个游戏对象具备刚体的BodyType均为Dynamic,但是Collision Detection属性不同的碰撞检测,阅读本文则默认已阅读前文。 (一)测试说明 在基于两个游戏对象都具…...

从前序与中序遍历序列构造二叉树
代码如下,开袋即食 class Solution {private Map<Integer,Integer> map;public TreeNode buildTree(int[] preorder, int[] inorder) {map new HashMap<>();for(int i 0;i<preorder.length;i){map.put(inorder[i],i);}return build(preorder,inord…...

antd5上传图片显示405解决
antd5上传图片,默认使用上传方式会调用本地的接口。 405 Method Not Allowed 状态码 405 Method Not Allowed 表明服务器禁止了使用当前 HTTP 方法的请求。 Upload {...props}beforeUpload{(file) > {//自定义上传图片的逻辑//最后返回falsereturn false }} &…...
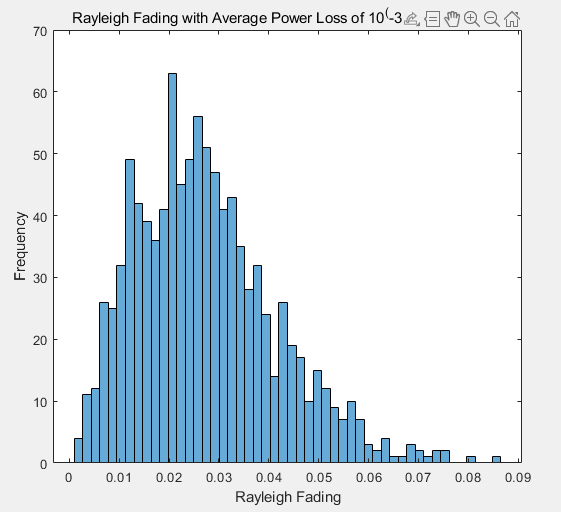
生成瑞利信道(Python and Matlab)
channel h k h_k hk is modeled as independent Rayleigh fading with average power loss set as 10^−3 Python import numpy as np# Set the parameters average_power_loss 1e-3 # Average power loss (10^(-3)) num_samples 1000 # Number of fading samples to …...

数据结构Demo——简单计算器
简单计算器 一、项目介绍二、技术使用三、具体代码实现1.前端部分2.后端部分 一、项目介绍 本项目实现了一个通过网页访问的简单计算器,它可以对带括号的加减乘除表达式进行计算并将计算结果返回给用户,并且可以对用户输入的表达式进行合法性判断&#…...

java实现多文件打包压缩,导出zip文件
一.实现多文件打包压缩 Testpublic void testZipFile() throws IOException {String filePath "D:\\导出压缩文件.zip";OutputStream outputStream new FileOutputStream(filePath);try (ZipOutputStream zipOutputStream new ZipOutputStream(outputStream)) {//…...

java-枚举类的使用
public enum MyEnum {ONE("一"),TWO("二"),THREE("三");private final String myNum;MyEnum(String myNum) {this.myNum myNum;}public String getMyEnum() {return myNum;} }调用 MyEnum num MyEnum.ONE; System.err.println(num.getMyEnum…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
