【机器学习】四、计算学习理论
1 基础知识
计算学习理论(computational learning theory):关于通过“计算”来进行“学习”的理论,即关于机器学习的理论基础,其目的是分析学习任务的困难本质,为学习算法体统理论保证,并根据结果指导算法设计。
对于二分类问题,给定样本集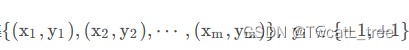
假设所有样本服从一个隐含未知的分布D DD,所有样本均独立同分布(independent and identically distributed)。
令h为样本到{ − 1 , + 1 } 上的一个映射,其泛化误差为
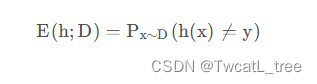
h在D 的经验误差为
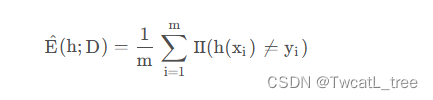
由于D是D的独立同分布采样,因此h hh的经验误差的期望等于其泛化误差。 在上下文明确时,我们将E ( h ; D ) 和E ^ ( h ; D ) 分别简记为E ( h )和E ^ ( h ) 。 令ϵ为E ( h ) 的上限,即E ( h ) ≤ ϵ E(h);我们通常用ϵ表示预先设定的学得模型所应满足的误差要求,亦称“误差参数”。
我们将研究经验误差和泛化误差之间的逼近程度;若h在数据集上的经验误差为0,则称h与D一致,否则称其不一致。对于任意两个映射h 1 , h 2 ∈ X → Y h_1,h_2,用不合(disagreement)来度量他们之间的差别:
d ( h 1 , h 2 ) = P x ∼ D ( h 1 ( x ) ≠ h 2 ( x ) )
我们将会用到几个常见的不等式:
Jensen不等式:对任意凸函数,有
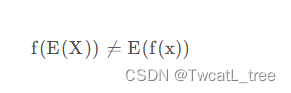
Hoeffding不等式:若x 1 , x 2 , … , x m
为m 个独立随机变量,且满足0 ≤ x i ≤ 1,对任意ϵ > 0,有
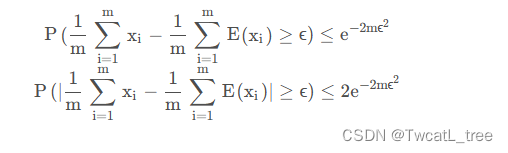
McDiarmid不等式:

2 PAC学习
概率近似正确理论(Probably Approximately Correct,PAC):
首先介绍两个概念:
C:概念类。表示从样本空间到标记空间的映射,对任意样例,都能使得c ( x ) = y 。
H :假设类。学习算法会把认为可能的目标概念集中起来构成H。
若c ∈ H ,则说明假设能将所有示例按真实标记一致的方式完全分开,称为该问题对学习算法而言是”可分的“;否则,称为”不可分的“
对于训练集,我们希望学习算法学习到的模型所对应的假设h hh尽可能接近目标概念c。我们是希望以比较大的把握学得比较好的模型,也就是说,以较大的概率学得误差满足预设上限的模型,这就是"概率近似正确"的含义。形式化地说,令δ 表示置信度,可定义:
PAC辨识:对0 ≤ ϵ , δ < 1 ,所有的c ∈ C 和分布D ,若存在学习算法,其输出假设h ∈ H 满足:



3 有限假设空间
3.1 可分情形

3.2 不可分情形

4 VC维

5 Rademacher复杂度

6 稳定性


相关文章:

【机器学习】四、计算学习理论
1 基础知识 计算学习理论(computational learning theory):关于通过“计算”来进行“学习”的理论,即关于机器学习的理论基础,其目的是分析学习任务的困难本质,为学习算法体统理论保证,并根据结…...
spring解决后端显示时区的问题
spring解决后端显示时区的问题 出现的问题: 数据库中的数据: 解决方法 spring:jackson:date-format: yyyy-MM-dd HH:mm:sstime-zone: Asia/Shanghai...

大模型冷思考:企业“可控”价值创造空间还有多少?
文 | 智能相对论 作者 | 叶远风 毫无疑问,大模型热潮正一浪高过一浪。 在发展进程上,从最开始的技术比拼到现在已开始全面强调商业价值变现,百度、科大讯飞等厂商都喊出类似“不能落地的大模型没有意义”等口号。 在模型类型上࿰…...

ctfshow-web入门37-52
include($c);表达式包含并运行指定文件。 使用data伪协议 ?cdata://text/plain;base64,PD9waHAgc3lzdGVtKCdjYXQgZmxhZy5waHAnKTs/Pg PD9waHAgc3lzdGVtKCdjYXQgZmxhZy5waHAnKTs/Pg 是<?php system(cat flag.php);?> base64加密 源代码查看得到flag 38 多禁用了ph…...

前端项目部署后,需要刷新页面才能看到更新内容
问题背景 前端项目部署更新后,通知业务验证,业务点击收藏的标签,打开网页后没有看到修改的内容,每次都需要手动刷新,用户体验非常不好。 问题原因:缓存未过期,浏览器直接读取本地缓存…...
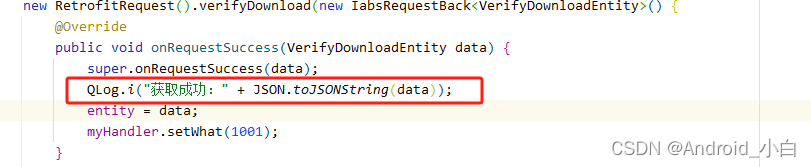
android 13 write javaBean error at *** 错误
报错代码:红框处。 注意:android10 不会报错,运行正常。android13就报错 错误原因:对象中VerifyDownloadEntity,有个Bitmap成员变量 public class VerifyDownloadEntity {private Bitmap bitmap;private String cooki…...

Only fullscreen opaque activities can request orientation
出现Only fullscreen opaque activities can request orientation是谷歌爸爸在安卓8.0版本时为了支持全面屏,增加了一个限制:如果是透明的Activity,则不能固定它的方向,因为它的方向其实是依赖其父Activity的(因为透明…...
前端实验(一)单页面应用的创建
实验目的 掌握使用vite创建vue3单页面程序命令熟悉所创建程序的组织结构熟悉单页面程序运行原理能够编写简单的单页面程序 实验内容 创建一个名为vue-demo的单页面程序编写简单的单页面程序页面运行单页面程序 实验步骤 使用vite创建单页面程序 创建项目名为目录vue-demo的…...

数字人小灿:始于火山语音,发于 B 端百业
火爆的数字人市场又有新消息来袭:火山语音的数字人小灿来了! 数字人小灿首曝视频 今年以来,在生成式AI浪潮的助推下,大量企业争相布局数字人赛道。市场之所以如此火热,是因为AI数字人已被视为人工智能时代智能交互的入…...

蓝桥杯刷题
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析(3) 👉🏻最大降雨量 原题链接࿱…...
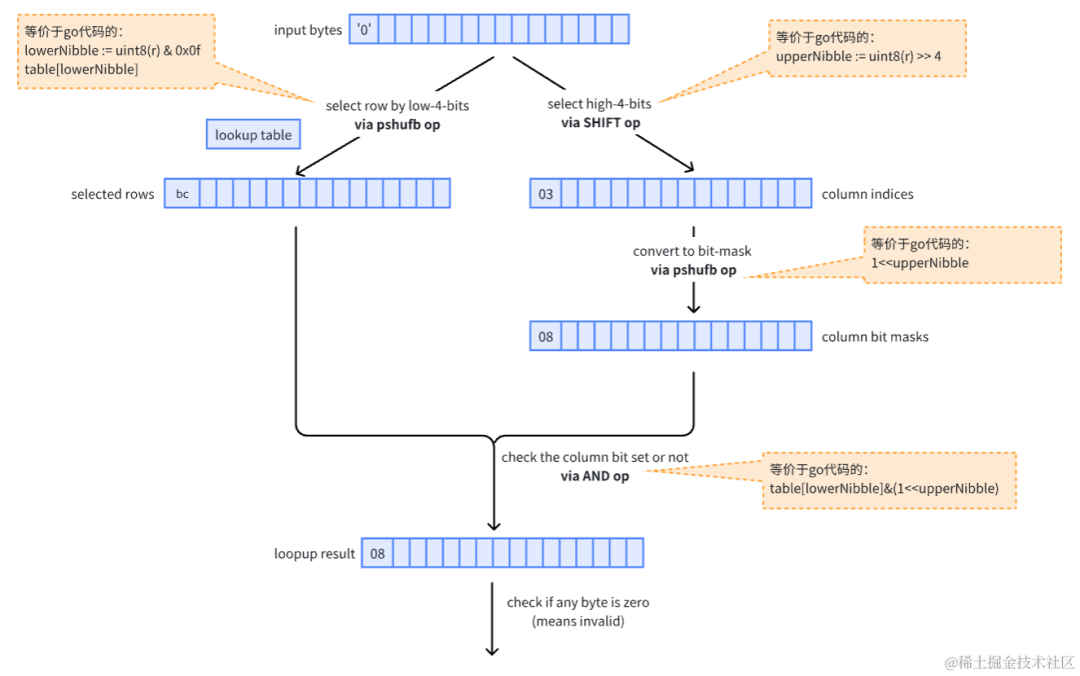
Go Metrics SDK Tag 校验性能优化实践
背景 Metrics SDK 是与字节内场时序数据库 ByteTSD 配套的用户指标打点 SDK,在字节内数十万服务中集成,应用广泛,因此 SDK 的性能优化是个重要和持续性的话题。本文主要以 Go Metrics SDK 为例,讲述对打点 API 的 hot-path 优化的…...
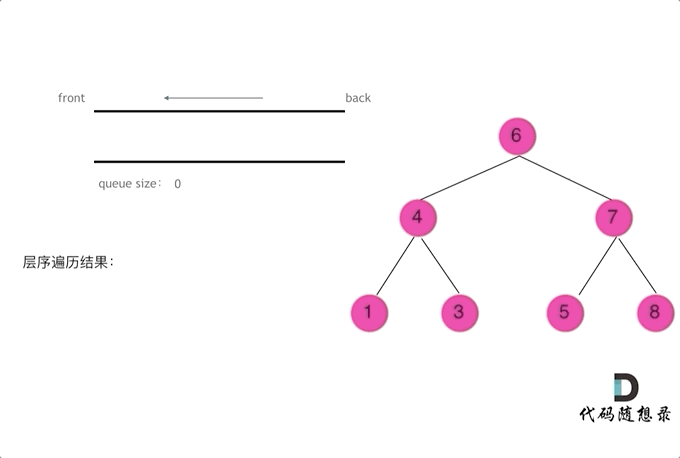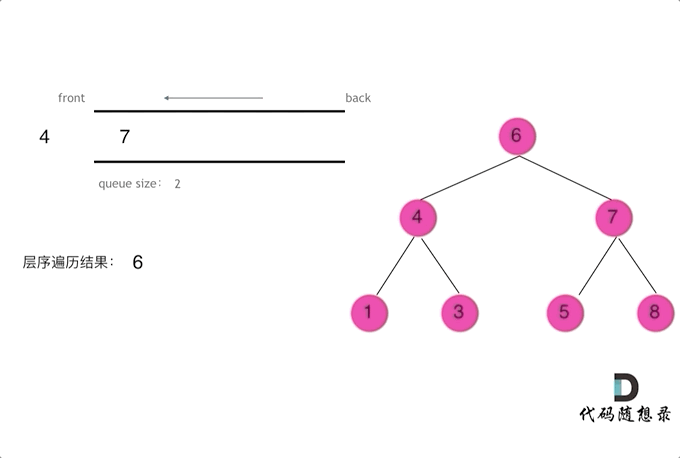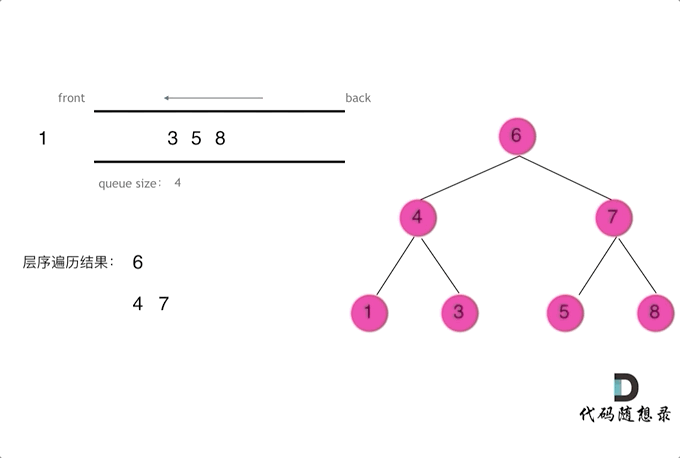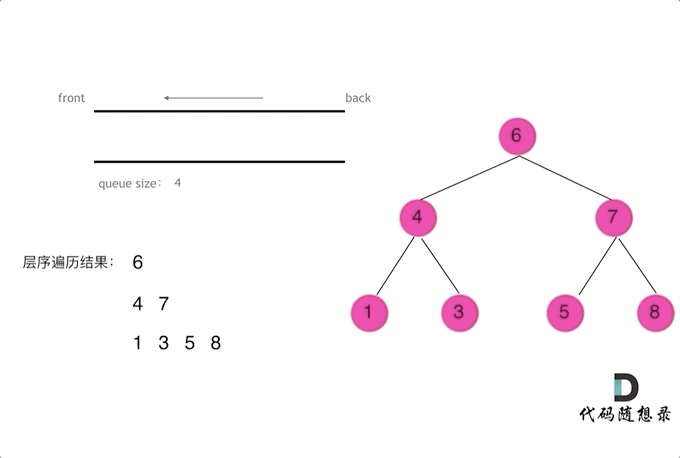
二叉树问题——前/中/后/层遍历问题(递归与栈)
摘要 博文主要介绍二叉树的前/中/后/层遍历(递归与栈)方法 一、前/中/后/层遍历问题 144. 二叉树的前序遍历 145. 二叉树的后序遍历 94. 二叉树的中序遍历 102. 二叉树的层序遍历 103. 二叉树的锯齿形层序遍历 二、二叉树遍历递归解析 // 前序遍历递归LC144_二叉树的前…...
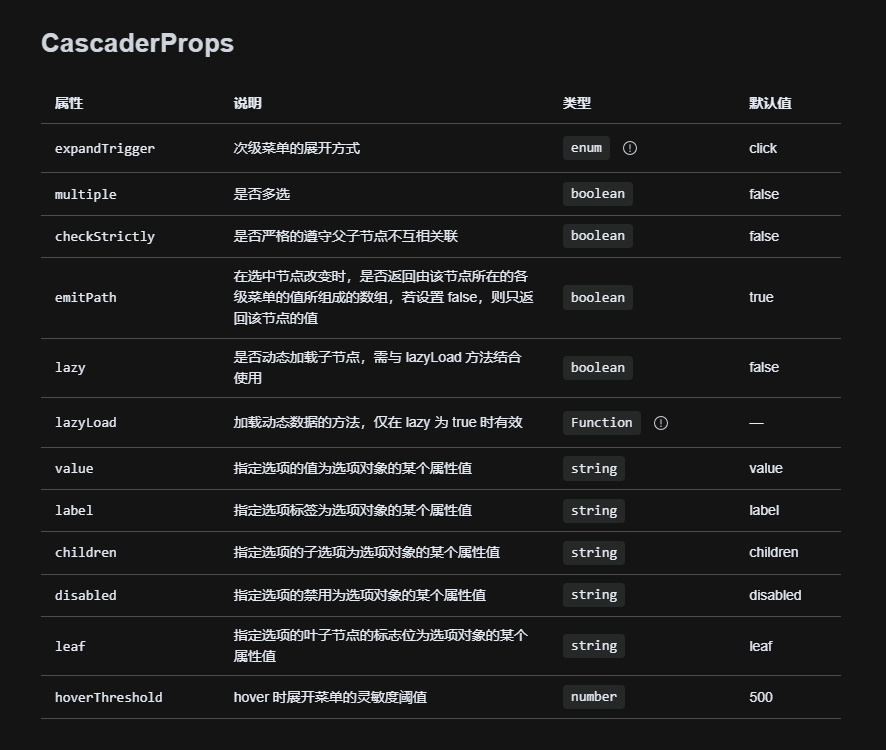
Vue3问题:如何实现级联菜单的数据懒加载?
前端功能问题系列文章,点击上方合集↑ 序言 大家好,我是大澈! 本文约3100字,整篇阅读大约需要5分钟。 本文主要内容分三部分,第一部分是需求分析,第二部分是实现步骤,第三部分是问题详解。 …...
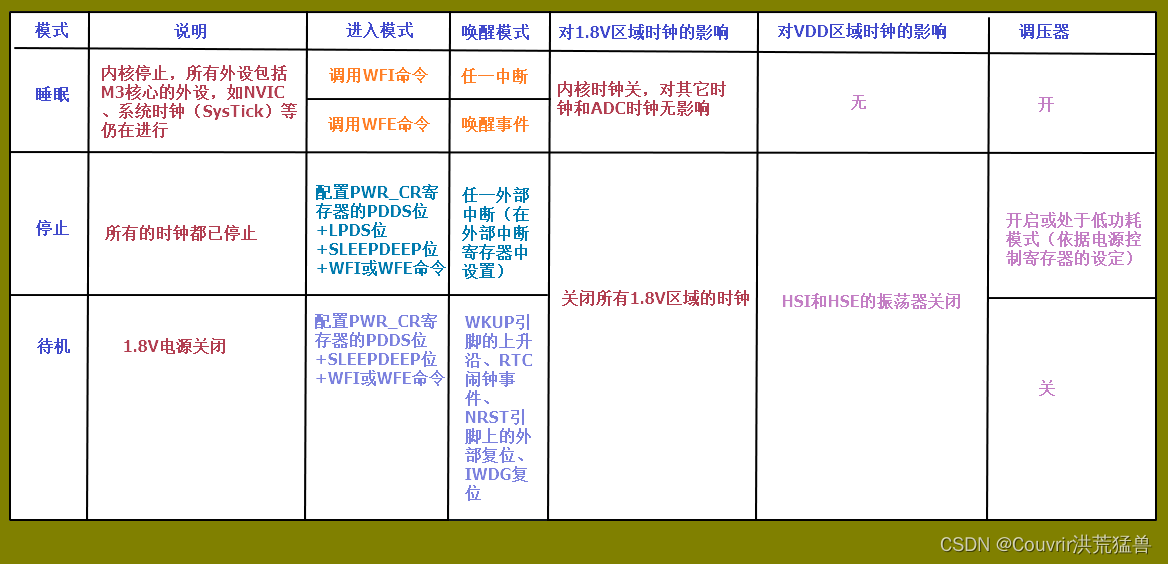
STM32-电源管理(实现低功耗)
电源管理 STM32 HAL库对电源管理提供了完善的函数和命令。 工作模式(高功耗->低功耗):运行、睡眠、停止、待机。 若备份域电源正常供电,备份域内的RTC都可以正常运行,备份域内的寄存器的数据会被保存,不…...
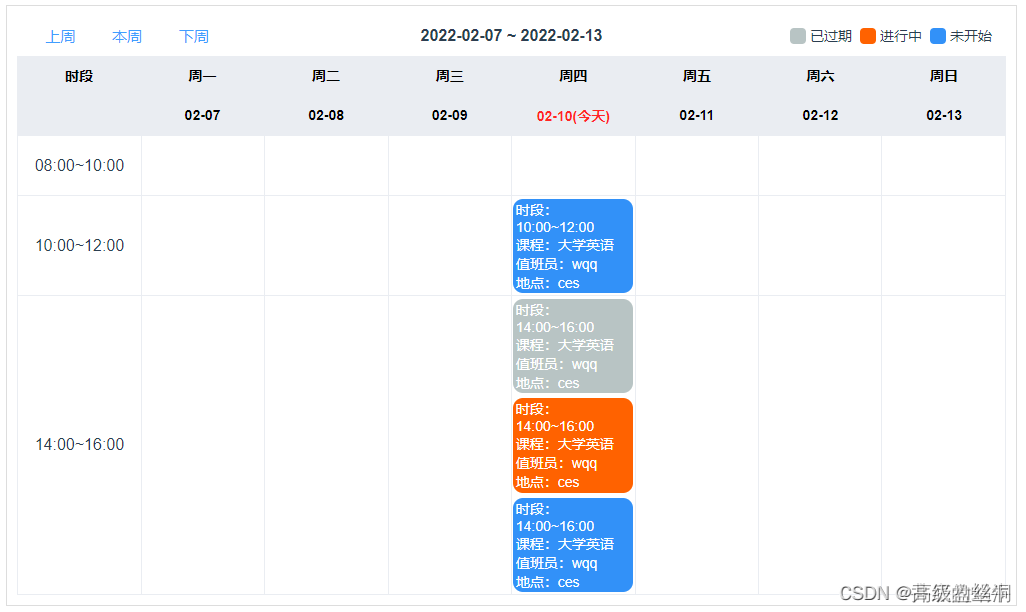
vue 自己捣鼓周日程日历组件
需求:想要一个周日程表,记录每天的计划,点击可查看详情。可自定义时间段通过后台获取时间段显示 分析: 通过需求,超级课程表app这款软件其中课表和这个需求很像,只不过这个需求第一列的时间段是自定义的,不是上午下午两个,但是原理都差不多 原本想找一些第三方插件使…...

【力扣】2127. (分类讨论 + 拓扑排序)参加会议的最多员工数
【力扣】2127. (分类讨论 拓扑排序)参加会议的最多员工数 文章目录 【力扣】2127. (分类讨论 拓扑排序)参加会议的最多员工数1. 题目介绍2. 思路(**分类讨论 拓扑排序**)3. 解题代码4. Danger参考 1. 题…...
使用教程)
Flutter——最详细(Map)使用教程
Map简介 键值对的集合,您可以使用其关联的键从中检索值。 普通的 HashMap是无序的(不保证顺序),LinkedHashMap 按键插入顺序迭代,而像 SplayTreeMap 这样的排序映射按排序顺序迭代键。 1,添加元素 addEntri…...

vue的入门第一课
Vue.js是一款流行的JavaScript框架,用于构建交互式Web应用程序。本文将详细介绍Vue.js的基础知识,包括Vue.js的历史、设计模式、构造函数参数、el、data、computed、method、watch以及差值的使用。 Vue.js是什么? Vue.js是一款用于构建用户…...

已解决:conda找不到对应版本的cudnn如何解决?
1.解决方法 配置深度学习环境时,打算安装cudatoolkit11.2和cudnn8.1,当使用conda install cudnn8.0时,却搜索不到这个版本的包,解决方法如下: conda search cudnn -c conda-forge然后就可以使用如下命令进行安装对应…...

大语言模型的学习路线和开源模型的学习材料《二》
第三层 LLMs to Artifact 第一重 langchain 【LLMs 入门实战 —— 十二 】基于 本地知识库 的高效 🤖langchain-ChatGLM 介绍:langchain-ChatGLM是一个基于本地知识的问答机器人,使用者可以自由配置本地知识,用户问题的答案也是基于本地知识生成的。【LLMs 入门实战 ——…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
