容斥原理,多步容斥
- 容斥意义法
设计状态表示容斥的过程。比较简单的容斥题目一般可以容斥意义。
如果我们要求方案数的话,通常情况下我们的把限制视为两个方面,一方面是总限制,一方面是对于每个物品的限制,这样设集合 S i S_i Si表示满足总限制以及对第 i i i个限制的方案构成的集合,若答案为 ∣ ⋃ n i = 1 S i ∣ \left| {\underset{i=1}{\overset{n}\bigcup}}S_i\right| i=1⋃nSi 或 ∣ ⋂ n i = 1 S i ∣ \left| {\underset{i=1}{\overset{n}\bigcap}}S_i\right| i=1⋂nSi ,则可以使用容斥原理求解。 - 容斥符号法
如果认为这个题是容斥,并且没什么太好的容斥想法,可以尝试容斥符号,例如把 = = =为 ≤ \leq ≤或 ≥ \geq ≥, = = =为 ⊆ , ⊇ \subseteq,\supseteq ⊆,⊇(例如把双射容斥为子集), ⊂ \subset ⊂为 ⊆ \subseteq ⊆ - 修正法
可以先编一个错误的答案,然后再考虑如何容斥掉多余的部分。很多较为复杂的题都可以修正。
容斥原理
一般的容斥原理就是设出集合,使得集合的并/交为答案,然后利用容斥原理求解的过程。
如果设不出集合,或者难以求解,则可以考虑更加复杂的计数方式,例如反演。
容斥原理:
补集转换 : S = U − S ‾ 补集转换:S=U-\overline{ S} 补集转换:S=U−S
德 ⋅ 摩根定律 : ⋃ n i = 1 S i ‾ = ⋂ n i = 1 S i ‾ , ⋂ n i = 1 S i ‾ = ⋃ n i = 1 S i ‾ 德·摩根定律:\overline{\underset{i=1}{\overset{n}{\bigcup}}S_i}=\underset{i=1}{\overset{n}{\bigcap}}\overline{S_i},\overline{\underset{i=1}{\overset{n}{\bigcap}}S_i }=\underset{i=1}{\overset{n}{\bigcup}}\overline{S_i} 德⋅摩根定律:i=1⋃nSi=i=1⋂nSi,i=1⋂nSi=i=1⋃nSi
集合的并 : ∣ ⋃ n i = 1 S i ∣ = ∑ ∅ ≠ T ⊆ [ n ] ( − 1 ) ∣ T ∣ − 1 ∣ ⋂ i ∈ T S i ∣ 集合的并:\left|\underset{i=1}{\overset{n}{\bigcup}}S_i \right|={\underset{\varnothing\not=T\subseteq [n]}{\overset{}\sum}}(-1)^{|T|-1}\left |{\underset{i\in T}{\overset{}\bigcap}}S_i\right | 集合的并: i=1⋃nSi =∅=T⊆[n]∑(−1)∣T∣−1 i∈T⋂Si
集合的交 : ∣ ⋂ n i = 1 S i ∣ = ∑ T ⊆ [ n ] ( − 1 ) ∣ T ∣ ∣ ⋂ i ∈ T S i ‾ ∣ 集合的交:\left| {\underset{i=1}{\overset{n}\bigcap}}S_i\right|={\underset{T\subseteq [n]}{\overset{}\sum}}(-1)^{|T|}\left|{\underset{i\in T}{\bigcap}\overline{S_i}}\right| 集合的交: i=1⋂nSi =T⊆[n]∑(−1)∣T∣ i∈T⋂Si
事实上求解集合的交的式子是由两步构成,根据德·摩根定律, ∣ ⋂ n i = 1 S i ∣ = U − ∣ ⋃ n i = 1 S i ‾ ∣ \left| {\underset{i=1}{\overset{n}\bigcap}}S_i\right|=U-\left| {\underset{i=1}{\overset{n}\bigcup}}\overline{S_i}\right| i=1⋂nSi =U− i=1⋃nSi
这说明集合的交=全集-补集的并,但是并集往往都比交集更难求解(除非集合之间没有交时,并集才好求解,但是我们在求解补集的并时,如果各个补集之间没有交,说明原集的并为全集,这样就不用求解了),因此我们注意到 ∣ ⋃ n i = 1 S i ‾ ∣ \left| {\underset{i=1}{\overset{n}\bigcup}}\overline{S_i}\right| i=1⋃nSi 也是集合的交集的形式,因此我们套用容斥原理进行求解,这样的过程叫做有人称为多步容斥。
补集转化
补集转化较简单。
有标号连通图计数
求 n n n个节点的无向连通图有多少个,节点有标号,编号为 [ 1 , n ] [1,n] [1,n]
n < = 5000 n<=5000 n<=5000
这个题是朴素容斥,即考虑如何用容斥原理来修正答案。
设 f i f_i fi表示大小为 i i i的连通图数量,一个想法是首先连出一棵树,但是不太好搞,考虑补集转换,总边数为 i ( i − 1 ) 2 \frac{i(i-1)}2 2i(i−1),总可能性为 h ( i ) = 2 i ( i − 1 ) 2 h(i)=2^{\frac {i(i-1)}2} h(i)=22i(i−1)种,减去不连通的情况即可,那我们枚举 1 1 1号点所在的连通块大小 j j j,然后从剩下的 i − 1 i-1 i−1个点中选出 j − 1 j-1 j−1个点,情况数量为: f j ( i − 1 j − 1 ) f_j \begin{pmatrix}i-1\\ j-1\end{pmatrix} fj(i−1j−1),剩下 i − j i-j i−j个点随意连边,转移方程为:
f i = h ( i ) − ∑ j < i f j ( i − 1 j − 1 ) h ( i − j ) f_i=h(i)-\underset{j<i}\sum f_j \begin{pmatrix}i-1\\ j-1\end{pmatrix}h(i-j) fi=h(i)−j<i∑fj(i−1j−1)h(i−j)
集合的交
容斥原理求解集合的交比较多,求解并反而比较少,因为题目往往要求同时遵守所有限制,而不是只遵守其中一个,这符合交的形式。
CF451E
限制 f i f_i fi是难以求解的,去掉 f i f_i fi的限制是好做的,很容易想到把它容斥掉。
容斥意义法:我们把选择 s s s朵花看做总限制,对第 i i i个花瓶的限制设出集合,则 S i S_i Si表示满足总共选了 s s s朵花,并且第 i i i个花瓶的花 ≤ f i \leq f_i ≤fi的方案的集合,则答案为 ∣ ⋂ n i = 1 S i ∣ \left| {\underset{i=1}{\overset{n}\bigcap}}S_i\right| i=1⋂nSi ,容易想到用容斥原理来求解。
则: ∣ ⋂ n i = 1 S i ∣ = ∑ T ⊆ [ n ] ( − 1 ) ∣ T ∣ ∣ ⋂ i ∈ T S i ‾ ∣ \left| {\underset{i=1}{\overset{n}\bigcap}}S_i\right|={\underset{T\subseteq [n]}{\overset{}\sum}}(-1)^{|T|}\left|{\underset{i\in T}{\bigcap}\overline{S_i}}\right| i=1⋂nSi =T⊆[n]∑(−1)∣T∣ i∈T⋂Si ,对于 T T T,我们要求出限制 i ∈ T i\in T i∈T均不合法的方案数,则我们指定物品 i i i至少选择了 f i + 1 f_i+1 fi+1次,剩下的次数为 s − ∑ i ∈ T ( f i + 1 ) s-\underset{i\in T}\sum (f_i+1) s−i∈T∑(fi+1),我们将它们划分到 n n n个花瓶中,根据集合的定义,我们不需要管这些花瓶的限制,这是隔板法问题,即 ( s − ∑ i ∈ T ( f i + 1 ) + n − 1 n − 1 ) \begin{pmatrix}s-\underset{i\in T}\sum (f_i+1)+n-1\\n-1\end{pmatrix} (s−i∈T∑(fi+1)+n−1n−1)。因此最终的式子就是: ∣ ⋂ n i = 1 S i ∣ = ∑ T ⊆ [ n ] ( − 1 ) ∣ T ∣ ( s − ∑ i ∈ T ( f i + 1 ) + n − 1 n − 1 ) \left| {\underset{i=1}{\overset{n}\bigcap}}S_i\right|={\underset{T\subseteq [n]}{\overset{}\sum}}(-1)^{|T|}\begin{pmatrix}s-\underset{i\in T}\sum (f_i+1)+n-1\\n-1\end{pmatrix} i=1⋂nSi =T⊆[n]∑(−1)∣T∣(s−i∈T∑(fi+1)+n−1n−1)
注:部分题解当中提到了“多重集的组合数”,很容易看成是“多重组合数”,但其实两者没啥关系。
代码(值域很大的组合数很难直接求解,我们把组合数转化为下降幂求解):
#include<iostream>
using namespace std;
const int N=20;
const long long M=1e9+7;
long long pow(long long a,long long b,long long c) {long long ans=1;while(b) {if(b&1) (ans=ans*a)%=M;(a=a*a)%=M;b>>=1;}return ans;
}
long long inv(long long x) {return pow(x,M-2,M);
}
long long a[N+5];
int n;
long long m;
long long d(long long x,long long k) {if(k==0) return 1;else return x%M*d(x-1,k-1)%M;
}
long long calc(int s) {long long sum=0;for(int i=1;i<=n;i++) if(s>>i-1&1) sum+=a[i]+1;if(m-sum<0) return 0;return d(m-sum+n-1,n-1)*inv(d(n-1,n-1))%M;
}
int main() {cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];long long ans=0;for(int s=0;s<1<<n;s++) (ans+=calc(s)*(__builtin_popcount(s)&1?-1:1))%=M;cout<<(ans%M+M)%M;
}
P1450
容易想到把 d i d_i di容斥掉。
容斥意义:我们把购买了价值为 s s s的物品作为总限制,把对硬币 i i i的数量的限制作为集合,则设 S i S_i Si表示满足对第 i i i个硬币数量限制,且购买了价值为 s s s的物品的方案的集合,则答案为 ∣ ⋂ 4 i = 1 S i ∣ \left| {\underset{i=1}{\overset{4}\bigcap}}S_i\right| i=1⋂4Si ,接下来根据 ∣ ⋂ n i = 1 S i ∣ = ∑ T ⊆ [ n ] ( − 1 ) ∣ T ∣ ∣ ⋂ i ∈ T S i ‾ ∣ \left| {\underset{i=1}{\overset{n}\bigcap}}S_i\right|={\underset{T\subseteq [n]}{\overset{}\sum}}(-1)^{|T|}\left|{\underset{i\in T}{\bigcap}\overline{S_i}}\right| i=1⋂nSi =T⊆[n]∑(−1)∣T∣ i∈T⋂Si ,我们要求解补集的交,即对于一些硬币的限制不满足的方案数。
如果硬币 i ∈ T i\in T i∈T的限制不满足,显然它选了至少 d i + 1 d_i+1 di+1个,我们提前dp出 f x f_x fx表示购买了价值为 s s s物品的完全背包方案数,则此时的方案数量为 f s − ∑ i ∈ T ( d i + 1 ) f_{s-\underset{i\in T}\sum(d_i+1)} fs−i∈T∑(di+1)。
则本次询问的答案为: ∣ ⋂ 4 i = 1 S i ∣ = ∑ T ⊆ [ 4 ] ( − 1 ) ∣ T ∣ f s − ∑ i ∈ T ( d i + 1 ) \left| {\underset{i=1}{\overset{4}\bigcap}}S_i\right|={\underset{T\subseteq [4]}{\overset{}\sum}}(-1)^{|T|}f_{s-\underset{i\in T}\sum(d_i+1)} i=1⋂4Si =T⊆[4]∑(−1)∣T∣fs−i∈T∑(di+1)
每做一次询问,我们就进行一次容斥,复杂度为 O ( 2 4 ) O(2^4) O(24),因此总复杂度为 ( n ⋅ 2 4 ) (n\cdot 2^4) (n⋅24)
#include<iostream>
#include<algorithm>
using namespace std;
const int R=100000;
long long f[R+5];
int a[10],b[10];
long long calc(int s,int x) {int t=1;while(s) x-=(s&1)*a[t]*(b[t]+1),s>>=1,t++;if(x<0) return 0;else return f[x];
}
int main() {int n;cin>>a[1]>>a[2]>>a[3]>>a[4]>>n;f[0]=1;for(int i=1;i<=4;i++)for(int j=a[i];j<=R;j++) f[j]+=f[j-a[i]];while(n--) {int x;cin>>b[1]>>b[2]>>b[3]>>b[4]>>x;long long ans=0;for(int i=0;i<1<<4;i++) ans+=calc(i,x)*(__builtin_popcount(i)&1?-1:1);
// cout<<"***";cout<<ans<<endl;}
}
UVA11806
将 k 个棋子放在 n × m n\times m n×m 的棋盘上。我们将连续的紧贴棋盘边界的放置棋子位置称为边缘。问上下左右四个边缘上都至少放置一个棋子的棋子放置方案共有多少种.
可以做到 n × m ≤ 1 0 5 , k ≤ 1 0 5 n\times m\leq 10^5,k\leq 10^5 n×m≤105,k≤105
容斥意义:我们总共四个边缘,我们设 S i S_i Si表示第 i i i个边缘有棋子的所有方案构成的集合,则答案为 ∣ ⋂ S ∣ \left|\bigcap S\right| ∣⋂S∣,求解补集相当于指定一些边缘没有棋子,剩下位置随意,容斥原理求解即可。
互质问题1
给出一个整数 n n n和一个整数 m m m,求 [ 1 , m ] [1,m] [1,m]之中有多少个数与 n n n互质。
1 ≤ n , m ≤ 1 0 18 1\leq n,m\leq 10^{18} 1≤n,m≤1018
首先我们会分析出来,如果与 n n n互质,则说明这个数不含有 n n n的任何一个质因子,因此可以容斥意义:设 S i S_i Si表示 [ 1 , m ] [1,m] [1,m]中不含有 n n n的第 i i i个本质不同质因子的数的集合,则答案为 ∣ ⋂ S i ∣ |\bigcap S_i| ∣⋂Si∣,对应的 T T T相当于求出 [ 1 , m ] [1,m] [1,m]之中有多少个数含有质因子集合 T T T,则方案数为 ⌊ m ∏ i ∈ T p i ⌋ \left\lfloor\frac m{\underset{i\in T}\prod p_i}\right\rfloor ⌊i∈T∏pim⌋。
这个容斥的时间复杂度为 O ( 2 ∣ P ∣ ) O\left(2^{|P|}\right) O(2∣P∣),其中 P P P表示 n n n的本质不同质因子构成的集合,则 ∣ P ∣ = O ( ln ln n ) |P|=O(\ln\ln n) ∣P∣=O(lnlnn)
互质问题2
给出一个整数 m m m,一个具有 n n n个元素的数组,求出 [ 1 , m ] [1,m] [1,m]中有多少个数与 n n n的所有元素互质:
n ≤ 20 , m ≤ 2 62 n\leq 20,m\leq 2^{62} n≤20,m≤262
首先会考虑到,与 n n n中所有元素互质,相当于没有 n n n中任何一个元素的任何一个质因子,因此我们可以将求出 n n n中的本质不同质因子集合,设为 P P P,则问题转化为求出 [ 1 , n ] [1,n] [1,n]当中有多少个数与 ∏ P \prod P ∏P互质。
POJ1091
给定 n n n个数,其数值取值范围为 [ 1 , m ] [1,m] [1,m],请问有多少种情况使得这 n n n个数与 m m m的最大公约数为 1 1 1。
n , m = 1 0 5 n,m=10^5 n,m=105
相当于对序列计数,满足: { a n } , a i ∈ [ 1 , m ] , gcd ( gcd n i = 1 { a i } , m ) = 1 \{a_n\},a_i\in[1,m],\gcd\left(\underset{i=1}{\overset n\gcd}\{a_i\},m\right)=1 {an},ai∈[1,m],gcd(i=1gcdn{ai},m)=1
我们会发现,如果序列的 gcd \gcd gcd与 m m m不互质,说明它含有 m m m的某些质因子,则说明序列中的每个数都含有这些质因子。因此我们可以用容斥意义来做这个题:设 S i S_i Si表示 m m m的第 i i i个本质不同质因子不出现在序列最大公约数的方案的集合,则答案为 ∣ ⋂ S i ∣ |\bigcap S_i| ∣⋂Si∣,那么补集为指定 m m m的质因子集合的子集 T T T是序列每一个元素的约数,也就是说序列每一个数都是 ∏ i ∈ T p i \underset{i\in T}\prod p_i i∈T∏pi的倍数,那这样的序列共有 ⌊ m ∏ i ∈ T p i ⌋ n \left\lfloor\frac m{\underset{i\in T}\prod p_i}\right\rfloor^n ⌊i∈T∏pim⌋n,容斥原理求解即可。
集合的并
HDU1796
题意简述:给出一个具有 n n n个元素的数组和一个整数 m m m,求出 [ 1 , m ] [1,m] [1,m]中有多少个数至少能整除 a a a数组中的一个数。
n ≤ 10 , a i , m ≤ 2 31 n\leq 10,a_i,m\leq 2^{31} n≤10,ai,m≤231
可以想到,能够整除 x x x的数的数量为 σ 0 ( x ) \sigma_0(x) σ0(x),能够整除 y y y的数量为 σ 0 ( y ) \sigma_0(y) σ0(y),还要在减去算重的数量,也就是既整除 x x x又整除 y y y的数,数量为 σ 0 ( gcd ( x , y ) ) \sigma_0(\gcd(x,y)) σ0(gcd(x,y))
其中 σ 0 \sigma_0 σ0表示约数个数函数。
容斥意义:我们把值域为 [ 1 , m ] [1,m] [1,m]作为总限制,对“能够整除 a i a_i ai”设计集合,则 S i S_i Si表示能够整除 a i a_i ai的数的集合,答案为 ∣ ⋃ n i = 1 S i ∣ \left|\underset{i=1}{\overset{n}{\bigcup}}S_i \right| i=1⋃nSi ,则我们根据 ∣ ⋃ n i = 1 S i ∣ = ∑ ∅ ≠ T ⊆ [ n ] ( − 1 ) ∣ T ∣ − 1 ∣ ⋂ i ∈ T S i ∣ \left|\underset{i=1}{\overset{n}{\bigcup}}S_i \right|={\underset{\varnothing\not=T\subseteq [n]}{\overset{}\sum}}(-1)^{|T|-1}\left |{\underset{i\in T}{\overset{}\bigcap}}S_i\right | i=1⋃nSi =∅=T⊆[n]∑(−1)∣T∣−1 i∈T⋂Si ,只需要求解集合的交即可。
也就是对于 T T T来说,求出是所有能够整除 i ∈ T i\in T i∈T的数的数量,也就是 σ 0 ( gcd i ∈ T { a i } ) \sigma_0\left({\underset{i\in T}\gcd \{a_i\}}\right) σ0(i∈Tgcd{ai}),因此答案为 ∣ ⋃ n i = 1 S i ∣ = ∑ ∅ ≠ T ⊆ [ n ] ( − 1 ) ∣ T ∣ − 1 σ 0 ( gcd i ∈ T { a i } ) \left|\underset{i=1}{\overset{n}{\bigcup}}S_i \right|={\underset{\varnothing\not=T\subseteq [n]}{\overset{}\sum}}(-1)^{|T|-1}\sigma_0\left({\underset{i\in T}\gcd \{a_i\}}\right) i=1⋃nSi =∅=T⊆[n]∑(−1)∣T∣−1σ0(i∈Tgcd{ai})
约数个数函数可以通过预处理质因子等手段求出。
时间复杂度为 O ( 2 n ) O(2^n) O(2n)
P3349
这个题还可以子集反演,本质上是一样的。不过这个题完全可以直接容斥。
我们要建立一个从树节点到图节点的映射 f f f,使得 f f f为一个双射,这是不好限制的,我们把它转化为, f f f共有 n n n个不同的像。
那我们设 S i S_i Si表示第 i i i个图节点是像的方案的集合,则答案为 ∣ ⋂ n i = 1 S i ∣ = ∑ T ⊆ [ n ] ( − 1 ) ∣ T ∣ ∣ ⋂ i ∈ T S i ‾ ∣ \left| {\underset{i=1}{\overset{n}\bigcap}}S_i\right|={\underset{T\subseteq [n]}{\overset{}\sum}}(-1)^{|T|}\left|{\underset{i\in T}{\bigcap}\overline{S_i}}\right| i=1⋂nSi =T⊆[n]∑(−1)∣T∣ i∈T⋂Si ,这样 T T T相当于求解指定一些图节点不能使用,剩下的节点随便。
设 s = [ n ] ⊕ T s=[n]\oplus T s=[n]⊕T,此时这个交集的大小是可以树形dp出来的,设 f u , i f_{u,i} fu,i表示dp到了树节点 u u u,节点 u u u对应图节点 i i i的方案数,则转移就是,对于 u u u的儿子 v v v对应的图节点为 j j j,只要 ( i , j ) (i,j) (i,j)在图上有连边,并且 i , j ∈ s i,j\in s i,j∈s,就可以转移:
void dfs(int u,int fa) {for(int v=1;v<=n;v++)if(b[u][v]&&(v^fa)) {dfs(v,u);for(int i=1; i<=n; i++)if(s>>i-1&1) {long long sum=0;for(int j=1; j<=n; j++)if(s>>j-1&1)if(a[i][j])sum+=f[v][j];f[u][i]*=sum;}}
}
显然初值为 f u , i ∈ s = 1 f_{u,i\in s}=1 fu,i∈s=1
模拟赛题

其中 n ≤ 20 , m ≤ 150 , k ≤ 7 , d ≤ 1 0 9 n\leq 20,m\leq 150,k\leq 7,d\leq 10^9 n≤20,m≤150,k≤7,d≤109
这个形式看起来非常的容斥,首先考虑没有 k k k的限制怎么做。这是个经典问题,设 f i , j f_{i,j} fi,j表示第 i i i秒在 j j j节点的方案数,就可以写出转移,观察到 n n n特别小, d d d特别大,因此可以矩阵快速幂加速转移。
那有了 k k k怎么做呢?首先可以子集反演,但是容斥意义还是更简单一点的。
设 S i S_i Si表示经过 i i i节点,到了第 d d d天的所有方案的集合,则答案为 ∣ ⋂ S i ∣ |\bigcap S_i| ∣⋂Si∣,补集相当于指定一些节点不能走,也就是禁止关于它们的转移,对于每个 T T T跑一次dp即可。
时间复杂度 O ( 2 k ⋅ n 3 ) O(2^k\cdot n^3) O(2k⋅n3)
后记
于是皆大欢喜。
相关文章:

容斥原理,多步容斥
容斥意义法 设计状态表示容斥的过程。比较简单的容斥题目一般可以容斥意义。 如果我们要求方案数的话,通常情况下我们的把限制视为两个方面,一方面是总限制,一方面是对于每个物品的限制,这样设集合 S i S_i Si表示满足总限制以及…...
vue(32) : win10创建vue2基础前端框架
vue2element-uiaxios 1.创建vue2项目 开发工具为HBuilderX 3.7.3 1.1.新建项目 1.2.普通项目-vue项目(2.6.10) 等待创建项目 2.安装element-ui组件 2.1右键左下角开始图标 2.2.cd进入项目目录,执行安装element-ui npm i element-ui -S 2.3.main.js引入配置 import {Paginat…...

如何制作一款资源网站app
简介 平时生活学习中我们会经常登录各种网站,比如看电影,看视频学习,找资料等等。有时想找到一个靠谱的网站,花了很长时间也找不到。我自己收集了很多好的网站,主要是找资源的,然后我做了一个导航app软件&…...
解决在Win7下运行一些老游戏花屏或色彩异常问题的方法
有一些喜欢回顾经典老游戏的玩家们,在目前最新的windows7的操作系统下,运行某些游戏会出现花屏,问题的原因是因为win7对这些游戏的DirectDraw不兼容,一种方法是改游戏配置文件,把游戏色彩8bit改成16bit,当然…...

使用vue3+vite+elctron构建小项目介绍Electron进程间通信
进程间通信 (IPC) 是在 Electron 中构建功能丰富的桌面应用程序的关键部分之一。 由于主进程和渲染器进程在 Electron 的进程模型具有不同的职责,因此 IPC 是执行许多常见任务的唯一方法,例如从 UI 调用原生 API 或从原生菜单触发 Web 内容的更改。 在 …...

家政APP开发服务同城预约维修接单管理系统软件小程序
家政服务小程序是一个基于移动端的家政服务平台,为用户提供方便快捷的家政服务。以下是小程序的主要功能: 1. 家政服务内容展示:商家可以在小程序中展示各种家政服务项目,如清洁、保洁、保姆、月嫂、钟点工等。用户可以浏览服务信…...

NOIP2023模拟8联测29 C. 蛋糕
NOIP2023模拟8联测29 C. 蛋糕 文章目录 NOIP2023模拟8联测29 C. 蛋糕题目大意思路code 题目大意 你现在得到了一个二维蛋糕,它从左到右可以分成 n n n 列,每列高为 a i a_i ai 。对于每一列,又可以从下到上分为 a i a_i ai 块&#x…...

echarts的图表立体感——实现立体柱状图和立体饼图的详细教程
😂博主:小猫娃来啦 😂文章核心:使用echarts实现立体柱状图和立体饼图的详细教程 文章目录 简单介绍立体柱状图和立体饼图环境配置实现立体柱状图实现立体饼图总结 简单介绍立体柱状图和立体饼图 立体柱状图和立体饼图是数据可视化…...

解决VSCode使用SSH远程连接时无法指定用户名的问题
Windows 11自带OpenSSH客户端,和VSCode配合得很好,没有这个问题。 今天要说的是旧版本Windows 7/8/10系统遇到的问题。 PS: Windows 7可以运行的最后版本是VSCode 1.80.2 由于Windows 7/8/10没有自带的OpenSSH客户端,但可以调用MSYS环境下的…...

Vue Camera是什么,如何用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 一、Vue Camera是什么? Vue Camera是一个基于Vue.js的相机组件库,…...

ORANGE室内高尔夫—韩国室内模拟高尔夫原装进口真实体验身临其境
ORANGE室内高尔夫—韩国室内模拟高尔夫 真实体验 身临其境 室内高尔夫的产品优势: 1. 实际高尔夫球场的限制:室内高尔夫可以弥补室外高尔夫球场数量有限的问题,使得更多人能够享受高尔夫运动。 2. 天气和季节的限制:室内高尔夫可…...

【观察】从口袋到云端全景式AI创新,联想“全栈智能”再升级
知名科技杂志《连线》创始主编凯文凯利曾预测:“在未来的 100 年里,人工智能将超越任何一种人工力量,将人类引领到一个前所未有的时代。” 确实如此,犹如历史上蒸汽机、电力、计算机和互联网等通用技术一样,近20年来&a…...

linux 实用命令搜集 —— 筑梦之路
1. xargs命令 # 找出 / 目录下以 .conf 结尾的文件,并进行文件分类find / -name *.conf -type f -print | xargs file# 找出文件并打包find / -name *.conf -type f -print | xargs tar cjf test.tar.gz 2. 查找内存使用量较高的进程 ps -aux | sort -rnk 4 | he…...
08-Docker-网络管理
Docker 在网络管理这块提供了多种的网络选择方式,他们分别是桥接网络、主机网络、覆盖网络、MACLAN 网络、无桥接网络、自定义网络。 1-无桥接网络(None Network) 当使用无桥接网络时,容器不会分配 IP 地址,也不会连…...

【VS Code】使用 VS Code 登陆远程服务器上的 Docker 容器
以下命令默认已经构建了一个 Docker Image。 # 在服务器上启动 docker (-p 端口映射,用于后续的 ssh 连接) docker run -itd -v /mnt/mount/:/home -p 8124:22 --name container-name --gpus all image-name# 进入容器中 docker exec -it container-name /bin/bas…...

用Python做数据分析之数据统计
接下来说说数据统计部分,这里主要介绍数据采样,标准差,协方差和相关系数的使用方法。 1、数据采样 Excel 的数据分析功能中提供了数据抽样的功能,如下图所示。Python 通过 sample 函数完成数据采样。 2、数据抽样 Sample 是进行…...
智慧工地建造平台源码、智慧化工地云平台源码
概述:智慧工地管理平台充分运用数字化技术,聚焦施工现场岗位一线,依托物联网、互联网、AI等技术,围绕施工现场管理的人、机、料、法、环五大维度,以及施工过程管理的进度、质量、安全三大体系为基础应用,实…...
Spring Cloud Alibaba中Nacos的安装(Windows平台)以及服务的发现
Spring Cloud Alibaba中Nacos的安装(Windows平台)以及服务的发现 下载安装Nacos解压启动验证是否启动搭建一个简单的Spring Cloud Alibaba项目Spring Cloud Alibaba 以及 Nacos的引入如何选择对应的版本 服务的注册Nacos相关组件的说明 下载安装Nacos G…...

QR码应用实战:Spring Boot与ZXing完美结合
🎏:你只管努力,剩下的交给时间 🏠 :小破站 QR码应用实战:Spring Boot与ZXing完美结合 前言第一: 介绍QR码和ZXing第二:springboot整合zxing添加ZXing依赖生成二维码生成条形码 前言 …...
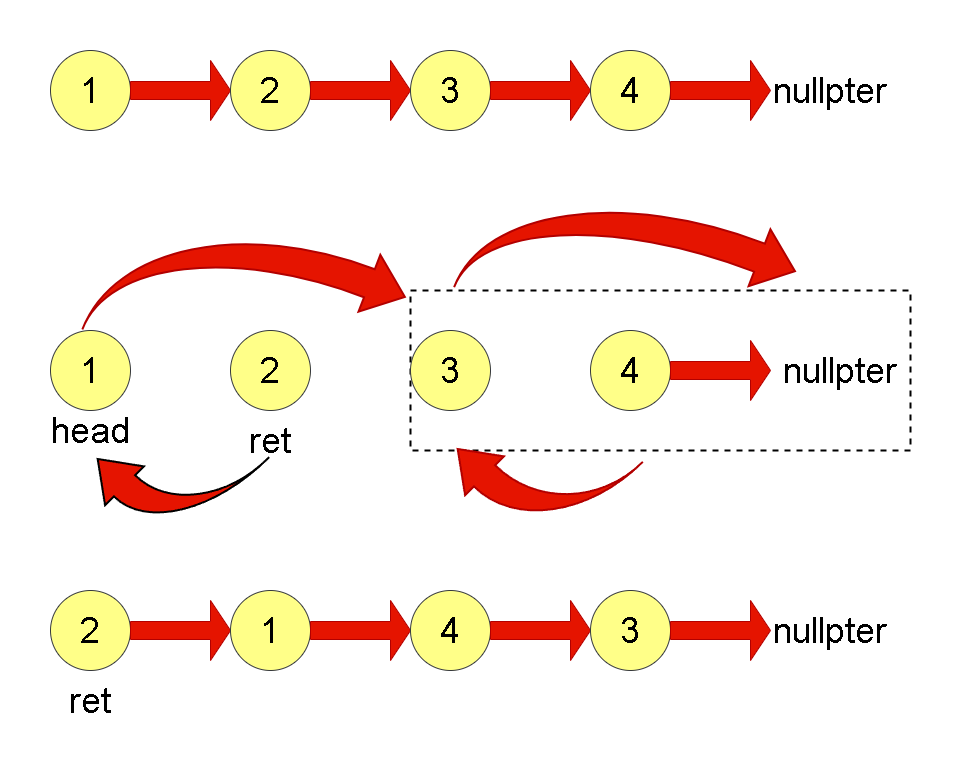
Leetcode刷题详解——两两交换链表中的节点
1. 题目链接:24. 两两交换链表中的节点 2. 题目描述: 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...

Qt/C++学习系列之列表使用记录
Qt/C学习系列之列表使用记录 前言列表的初始化界面初始化设置名称获取简单设置 单元格存储总结 前言 列表的使用主要基于QTableWidget控件,同步使用QTableWidgetItem进行单元格的设置,最后可以使用QAxObject进行单元格的数据读出将数据进行存储。接下来…...

八、【ESP32开发全栈指南:UDP客户端】
1. 环境准备 安装ESP-IDF v4.4 (官方指南)确保Python 3.7 和Git已安装 2. 创建项目 idf.py create-project udp_client cd udp_client3. 完整优化代码 (main/main.c) #include <string.h> #include "freertos/FreeRTOS.h" #include "freertos/task.h&…...
