NOIP2023模拟8联测29 C. 蛋糕
NOIP2023模拟8联测29 C. 蛋糕
文章目录
- NOIP2023模拟8联测29 C. 蛋糕
- 题目大意
- 思路
- code
题目大意
你现在得到了一个二维蛋糕,它从左到右可以分成 n n n 列,每列高为 a i a_i ai 。对于每一列,又可以从下到上分为 a i a_i ai 块,并且最上面一块权值为 1 1 1 ,从上到下权值依次加 。每一列的最上面的权值为 的块的上表面有“奶油”。
你现在要把这一个蛋糕分成若干个矩形,要求每一个矩形上都要有“奶油”,也即每个矩形要包含至少一个权值为 1 1 1 的块。显然蛋糕中的每一格都必须被划分到恰好一个矩形内,且矩形不能包含没有蛋糕的格子。
定义每一块矩形的代价为其每一行的最大值之和,即 ∑ i = l r ( max j − = d u v i , j ) \sum_{i = l}^r(\max_{j -= d}^u v_{i , j}) ∑i=lr(maxj−=duvi,j) 。特别地,对于宽(列数)为 1 1 1 的矩形,代价为矩形内权值的最大值。请你最小化划分整个蛋糕的代价。
n ≤ 3000 n\le 3000 n≤3000
思路
考虑维护区间最大值和最小值的位置。
然后搞一个 d p l , r , k dp_{l , r , k} dpl,r,k 表示区间 [ l , r ] [l , r] [l,r] 内从下往上前 k k k 层的最小代价。
通过一通推理发现,对于一个区间 [ l , r ] [l , r] [l,r] 的最优策略就是删除最高的那一列或者把区间的所有蛋糕删到最矮的那一列那么高。
搞一个记忆化就好了
code
#include <bits/stdc++.h>
#define LL long long
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
const int N = 3005;
int n , min1[N][N] , max1[N][N];
LL a[N];
map<LL , LL> dp;
LL gt (LL l , LL r , LL k) { return (l * (N + 1) + r) * N + k; }
LL getsum (LL x , LL y) { return (x + y) * (y - x + 1) / 2; }
LL solve (int l , int r , LL k) {LL id = gt (l , r , k);if (dp.count (id)) return dp[id];int mxd = max1[l][r] , mnd = min1[l][r];LL ans = a[mxd] - k;if (mxd > l) ans += solve (l , mxd - 1 , k);if (mxd < r) ans += solve (mxd + 1 , r , k);if (l != r) {LL ans1 = getsum (a[mxd] - a[mnd] + 1 , a[mxd] - k);if (l < mnd) ans1 += solve (l , mnd - 1 , a[mnd]);if (mnd < r) ans1 += solve (mnd + 1 , r , a[mnd]);ans = min (ans , ans1);}return dp[id] = ans;
}
int main () {freopen ("cake.in" , "r" , stdin);freopen ("cake.out" , "w" , stdout);scanf ("%d" , &n); fu (i , 1 , n) {scanf ("%lld" , &a[i]);}fu (l , 1 , n) {min1[l][l] = max1[l][l] = l;fu (r , l + 1 , n) {min1[l][r] = min1[l][r - 1] , max1[l][r] = max1[l][r - 1];if (a[min1[l][r - 1]] > a[r]) min1[l][r] = r;if (a[max1[l][r - 1]] < a[r]) max1[l][r] = r;}}
// return 0;printf ("%lld" , solve (1 , n , 0));return 0;
}相关文章:

NOIP2023模拟8联测29 C. 蛋糕
NOIP2023模拟8联测29 C. 蛋糕 文章目录 NOIP2023模拟8联测29 C. 蛋糕题目大意思路code 题目大意 你现在得到了一个二维蛋糕,它从左到右可以分成 n n n 列,每列高为 a i a_i ai 。对于每一列,又可以从下到上分为 a i a_i ai 块&#x…...

echarts的图表立体感——实现立体柱状图和立体饼图的详细教程
😂博主:小猫娃来啦 😂文章核心:使用echarts实现立体柱状图和立体饼图的详细教程 文章目录 简单介绍立体柱状图和立体饼图环境配置实现立体柱状图实现立体饼图总结 简单介绍立体柱状图和立体饼图 立体柱状图和立体饼图是数据可视化…...

解决VSCode使用SSH远程连接时无法指定用户名的问题
Windows 11自带OpenSSH客户端,和VSCode配合得很好,没有这个问题。 今天要说的是旧版本Windows 7/8/10系统遇到的问题。 PS: Windows 7可以运行的最后版本是VSCode 1.80.2 由于Windows 7/8/10没有自带的OpenSSH客户端,但可以调用MSYS环境下的…...

Vue Camera是什么,如何用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 一、Vue Camera是什么? Vue Camera是一个基于Vue.js的相机组件库,…...

ORANGE室内高尔夫—韩国室内模拟高尔夫原装进口真实体验身临其境
ORANGE室内高尔夫—韩国室内模拟高尔夫 真实体验 身临其境 室内高尔夫的产品优势: 1. 实际高尔夫球场的限制:室内高尔夫可以弥补室外高尔夫球场数量有限的问题,使得更多人能够享受高尔夫运动。 2. 天气和季节的限制:室内高尔夫可…...

【观察】从口袋到云端全景式AI创新,联想“全栈智能”再升级
知名科技杂志《连线》创始主编凯文凯利曾预测:“在未来的 100 年里,人工智能将超越任何一种人工力量,将人类引领到一个前所未有的时代。” 确实如此,犹如历史上蒸汽机、电力、计算机和互联网等通用技术一样,近20年来&a…...

linux 实用命令搜集 —— 筑梦之路
1. xargs命令 # 找出 / 目录下以 .conf 结尾的文件,并进行文件分类find / -name *.conf -type f -print | xargs file# 找出文件并打包find / -name *.conf -type f -print | xargs tar cjf test.tar.gz 2. 查找内存使用量较高的进程 ps -aux | sort -rnk 4 | he…...
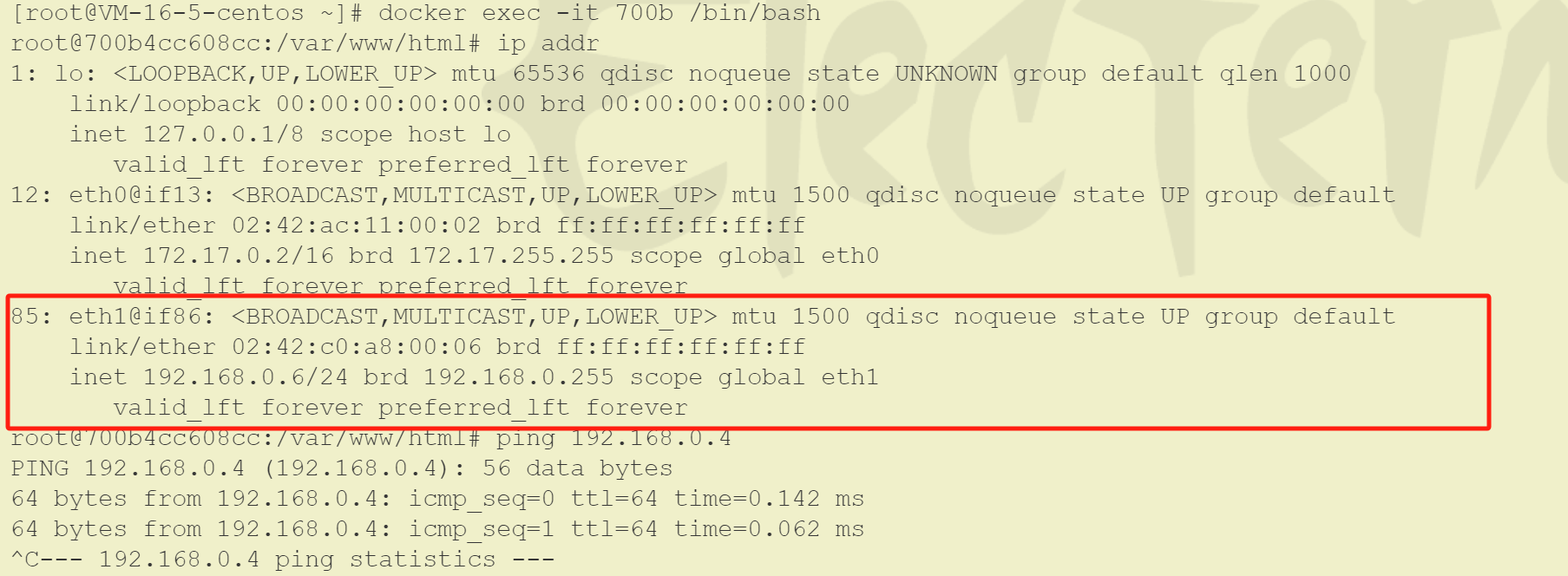
08-Docker-网络管理
Docker 在网络管理这块提供了多种的网络选择方式,他们分别是桥接网络、主机网络、覆盖网络、MACLAN 网络、无桥接网络、自定义网络。 1-无桥接网络(None Network) 当使用无桥接网络时,容器不会分配 IP 地址,也不会连…...

【VS Code】使用 VS Code 登陆远程服务器上的 Docker 容器
以下命令默认已经构建了一个 Docker Image。 # 在服务器上启动 docker (-p 端口映射,用于后续的 ssh 连接) docker run -itd -v /mnt/mount/:/home -p 8124:22 --name container-name --gpus all image-name# 进入容器中 docker exec -it container-name /bin/bas…...

用Python做数据分析之数据统计
接下来说说数据统计部分,这里主要介绍数据采样,标准差,协方差和相关系数的使用方法。 1、数据采样 Excel 的数据分析功能中提供了数据抽样的功能,如下图所示。Python 通过 sample 函数完成数据采样。 2、数据抽样 Sample 是进行…...
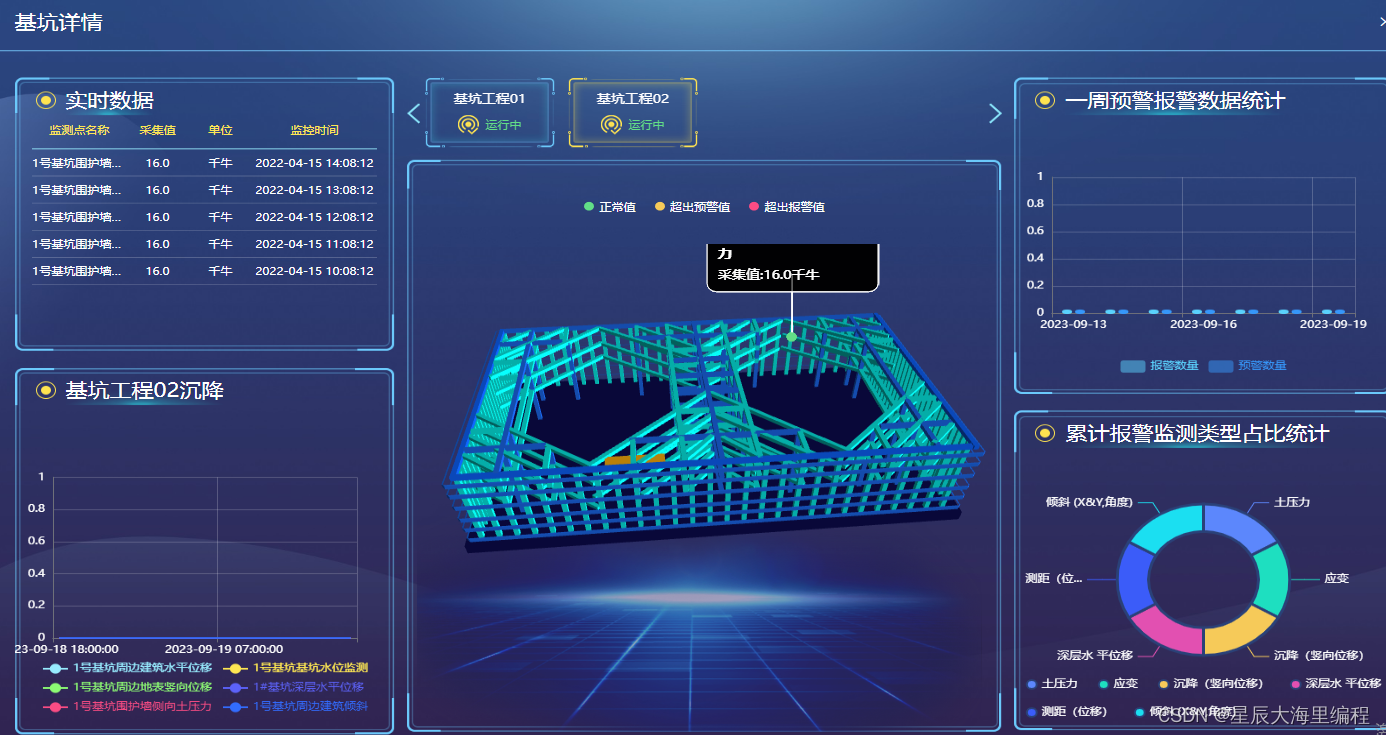
智慧工地建造平台源码、智慧化工地云平台源码
概述:智慧工地管理平台充分运用数字化技术,聚焦施工现场岗位一线,依托物联网、互联网、AI等技术,围绕施工现场管理的人、机、料、法、环五大维度,以及施工过程管理的进度、质量、安全三大体系为基础应用,实…...
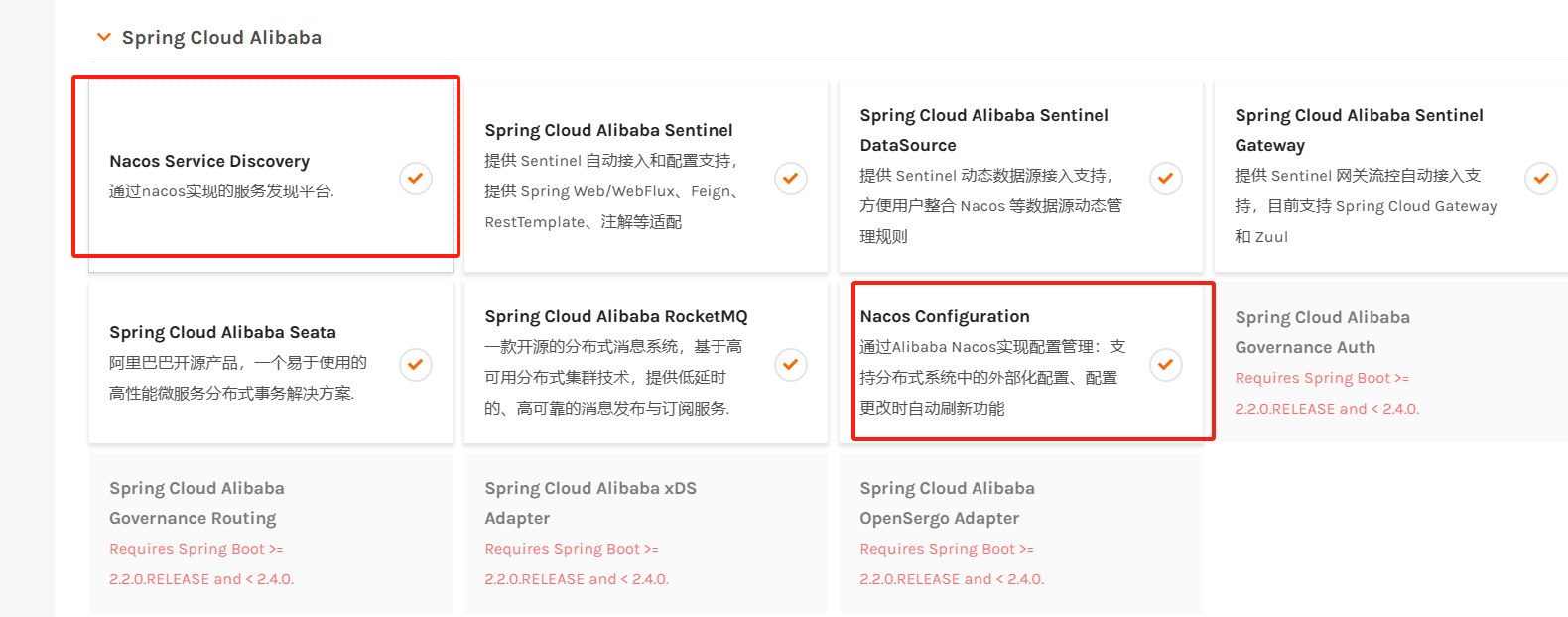
Spring Cloud Alibaba中Nacos的安装(Windows平台)以及服务的发现
Spring Cloud Alibaba中Nacos的安装(Windows平台)以及服务的发现 下载安装Nacos解压启动验证是否启动搭建一个简单的Spring Cloud Alibaba项目Spring Cloud Alibaba 以及 Nacos的引入如何选择对应的版本 服务的注册Nacos相关组件的说明 下载安装Nacos G…...

QR码应用实战:Spring Boot与ZXing完美结合
🎏:你只管努力,剩下的交给时间 🏠 :小破站 QR码应用实战:Spring Boot与ZXing完美结合 前言第一: 介绍QR码和ZXing第二:springboot整合zxing添加ZXing依赖生成二维码生成条形码 前言 …...
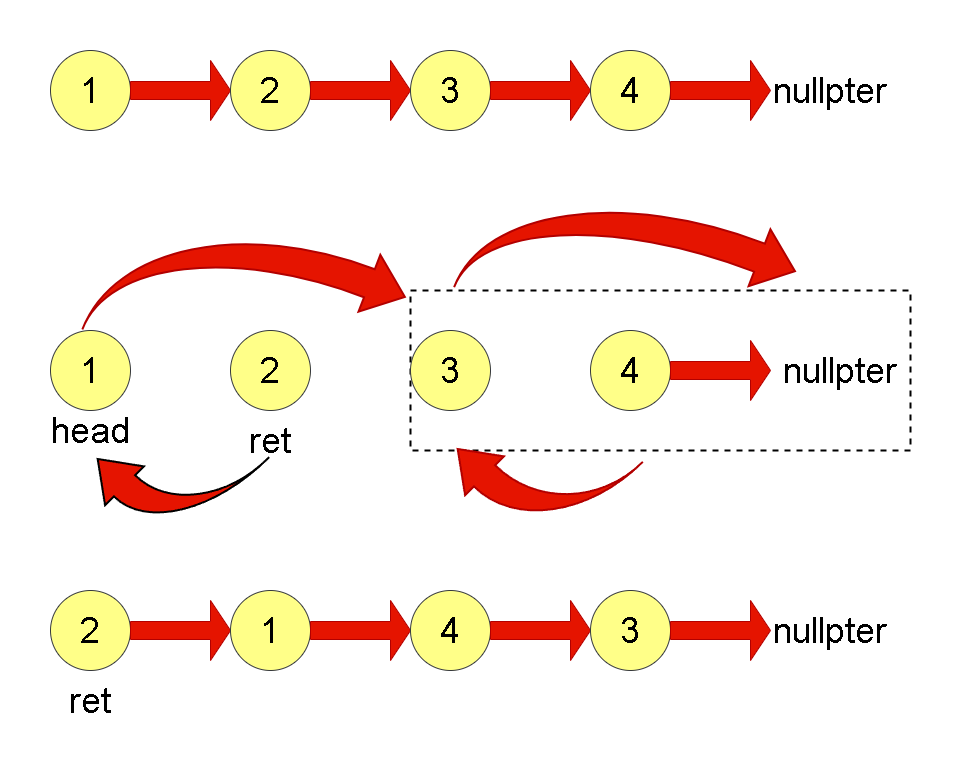
Leetcode刷题详解——两两交换链表中的节点
1. 题目链接:24. 两两交换链表中的节点 2. 题目描述: 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 …...
Openssl数据安全传输平台019:外联接口类的封装以及动态库的制作 - Bug未解决,感觉不是代码的问题
文章目录 1 外联接口1.1 接口类的封装1.2 共享内存与配置文件 2 json格式配置文件的定义2.1 共享内存中存储的节点结构2.2 服务器端配置文件2.3 客户端配置文件2.4 改进配置文件 3 共享内存类修改4 将接口打包成库(静态/动态)4.1 相关的指令4.1.1 静态库4.1.2 动态库 4.2 外联接…...

YOLO目标检测——安全帽佩戴检测数据集【含对应voc、coco和yolo三种格式标签】
实际项目应用:安全帽佩戴检测数据集可以用于实时检测工作人员是否按照要求佩戴了安全帽,以保障他们的安全数据集说明:安全帽佩戴检测数据集,真实场景的高质量图片数据,数据场景丰富,图片分为带头盔和没带头…...

P4345 [SHOI2015] 超能粒子炮·改 题解---------Lucas定理
题面: 题目 题意概括: T T T 次询问,每次给出 n , k n,k n,k,求 ∑ i 0 k C n i % 2333 \sum_{i 0}^{k} C_{n}^{i} \ \% \ 2333 ∑i0kCni % 2333。 1 ≤ T ≤ 1 0 5 , 1 ≤ n , k ≤ 1 0 18 1\leq T \leq10^5…...

http代理和ip代理的区别,代理IP带来了哪些好处?
随着互联网的快速发展,代理IP和HTTP代理已成为网络爬虫、网络营销、数据抓取等领域中不可或缺的一部分。但是,很多人在使用代理IP和HTTP代理时并不清楚两者的区别,以及代理IP所带来的好处。本文将详细介绍这两者之间的差异,以及代…...

浅谈电动汽车充电桩检测技术的实现
叶根胜 安科瑞电气股份有限公司 上海嘉定 201801 摘要: 关键词:电动直流和交流充电桩是我国电动汽车充电桩中运行量较大的一种。为了保持正常运行和使用,应高度重视检测、运行和维护工作。因此,有关部门应做好充电桩的检测工作…...

20 分钟搭建一个串流服务器
步骤1:准备Nginx RTMP容器 首先,您可以使用官方的Nginx RTMP Docker镜像来创建Nginx RTMP容器。运行以下命令: docker run -d -p 1935:1935 --name nginx-rtmp tiangolo/nginx-rtmp 这将在后台运行Nginx RTMP容器,将本地1935端…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...
