16. 机器学习 - 决策树

Hi,你好。我是茶桁。
在上一节课讲SVM之后,再给大家将一个新的分类模型「决策树」。我们直接开始正题。
决策树
我们从一个例子开始,来看下面这张图:

假设我们的x1 ~ x4是特征,y是最终的决定,打比方说是买东西和不买东西,0为不买,1为买东西,假设现在y是[0,0,1,0,1]。
那么,我们应该以哪个特征为准去判断到底y是0还是1呢?
如果关注x3,那么x3为A的时候,即有0也有1,我们先放一边找找看有没有更合适的。
如果是x4的话,肉眼可见的,区分度是最准确的对吧?B的都是都是0,C的时候都是1,那么x4也就是区分度最大的。
我们现在换成人的思维过程来说,肯定是期望先找到那个最能区分它的,就是最能识别的特征。这个最能识别的特征在数学里面有一个专门的定义:Salient feature, 就是显著特征。
如果我们更改一下x4的值,变成[B,C,C,B,B], 那x4也就不那么显著了。这个时候最能区分的就是x2了,只在x2[1]的位置上判断错了一个。
这个时候,我们就需要客观的衡量一下,什么叫做最能区分,或者说是最能分割,最显著的区别。这就需要一个专门的数值来计算。
那我们就来看看,到底怎么样来做区分。我们现在根据一个值,将我们的数据分成了两堆,那咱们的期望就是这两堆数据尽可能是一样的。比如极端情况下,一堆全是0, 一堆全是1,当然,中间混进去一个不一样的也行,但是尽可能的「纯」:

好,那我们该怎么定义这个「纯」呢?
我们大家应该都知道物理里有一个定义:「熵」,那熵在物理里是衡量物体的混乱程度的。
比如说一个组织、一个单位、公司或者个人,其内部的熵都是在呈现越来越混乱,而且熵的混乱具有不可逆性。这个呢,就是熵增定律,也叫「热力学第二定律」。是德国人克劳修斯提出的理论,最初用于揭示事物总是向无序的方向的发展、以及“孤立系统下热量从高温物体流向低温不可逆”的热力学定律(要不说看我的文章涨学问呢是吧)。
信息熵
好,说回咱们的机器学习。后来有一个叫「香农」的人要衡量一堆新息的混乱程度,就起了一个名字「信息熵」,也就成了衡量信息的复杂程度。
那么信息熵怎么求呢?
E n t r o p y = ∑ i = 1 n − p ( c i ) l o g 2 ( p ( c i ) ) \begin{align*} Entropy = \sum_{i=1}^n-p(c_i)log_2(p(c_i)) \end{align*} Entropy=i=1∑n−p(ci)log2(p(ci))
这个值越大,就说明了这个新息越混乱,相反的,越小就说明越有秩序。来,我们看一下代码演示,定义一个熵的方法:
import numpy as np
from icecream import ic
from collections import Counterdef pr(e, elements):counter = Counter(elements)return counter[e] / len(elements)# 信息熵
def entropy(elements):return -np.sum(pr(e, element) * np.log(pr(e, elements)) for e in elements)
然后我们具体的来看几组数据:
ic(entropy([1,1,1,1,1,0]))
ic(entropy([1,1,1,1,1,1]))
ic(entropy([1,2,3,4,5,8]))
ic(entropy([1,2,3,4,5,9]))
ic(entropy(['a','b','c','c','c','c','c']))
ic(entropy(['a','b','c','c','c','c','d']))---
ic| entropy([1,1,1,1,1,0]): 1.05829973151282
ic| entropy([1,1,1,1,1,1]): -0.0
ic| entropy([1,2,3,4,5,8]): 1.7917594692280547
ic| entropy([1,2,3,4,5,9]): 1.7917594692280547
ic| entropy(['a','b','c','c','c','c','c']): 1.7576608876629927
ic| entropy(['a','b','c','c','c','c','d']): 2.1130832934475294
我们可以看到,最「纯」的是第二行数据,然后是第一行,第三行和第四行是一样的。5,6行就更混乱一些。
那接下来的知识点是只关于Python的,我们看上面的代码是不是有点小问题?这个代码里有很多的冗余。一般情况下,会将counter改成全局变量,但是一般如果想要代码质量好一些,尽量不要轻易定义全局变量。我们来简单的修改一下:
def entropy(elements):# 信息熵def pr(es):counter = Counter(es)def _wrap(e):return counter[e] / len(elements)return _wrapp = pr(elements)return -np.sum(p(e) * np.log(p(e)) for e in elements)
这样写之后,我们再用刚才的数据来进行调用会看到结果完全一样。不过如果这样写之后,如果我们数据量很大的情况下,会发现会快很多。
Gini系数
除了上面这个信息熵之外,还有一个叫Gini系数,和信息熵很类似:
G i n i = 1 − ∑ i = 1 n p 2 ( C i ) \begin{align*} Gini = 1 - \sum_{i=1}^np^2(C_i) \\ \end{align*} Gini=1−i=1∑np2(Ci)
假如说probability都是1,也就是最纯的情况,那么1减去1就等于0。如果它特别长,特别混乱,都很分散,那probability就会越接近于0,那么1减去0,那结果也就是越接近于1。
那么代码实现一下就是这样:
def geni(elements):return 1-np.sum(pr(e) ** 2 for e in set(elements))
好吧,这个时候我发现一个问题,之前我们将probability函数定义到熵函数内部了,为了让Gini函数能够调用,我们还得拿出来。在我们之前修改的初衷不变的情况下,我们来这样进行修改:
def pr(es):counter = Counter(es)def _wrap(e):return counter[e] / len(es)return _wrapdef entropy(elements):# 信息熵p = pr(elements)return -np.sum(p(e) * np.log(p(e)) for e in elements)
哎,这样就对了。优雅…
然后我们来修改Gini函数,让其调用pr函数:
def gini(elements):p = pr(elements)return 1 - np.sum(p(e) ** 2 for e in set(elements))
然后我们写一个衡量的方法:
pure_func = gini
然后我们将之前的调用都修改一下:
ic(pure_func([1,1,1,1,1,0]))
ic(pure_func([1,1,1,1,1,1]))
ic(pure_func([1,2,3,4,5,8]))
ic(pure_func([1,2,3,4,5,9]))
ic(pure_func(['a','b','c','c','c','c','c']))
ic(pure_func(['a','b','c','c','c','c','d']))---
ic| pure_func([1,1,1,1,1,0]): 0.2777777777777777
ic| pure_func([1,1,1,1,1,1]): 0.0
ic| pure_func([1,2,3,4,5,8]): 0.8333333333333333
ic| pure_func([1,2,3,4,5,9]): 0.8333333333333333
ic| pure_func(['a','b','c','c','c','c','c']): 0.44897959183673464
ic| pure_func(['a','b','c','c','c','c','d']): 0.6122448979591837
我们可以看到,Gini系数是把整个纯度压缩到了0~1之间,越接近于1就是越混乱,越接近0呢就是越有秩序。
其实除了数组之外,字符串也是一样可以衡量的:
ic(pure_func("probability"))
ic(pure_func("apple"))
ic(pure_func("boom"))---
ic| pure_func("probability"): 0.8760330578512396
ic| pure_func("apple"): 0.72
ic| pure_func("boom"): 0.625
在能够定义纯度之后,现在如果我们有很多数据,就比方说是我们最之前定义数据再增多一些:[x1, x2, x3, ..., xn],那么我们决策树会做什么呢?
根据x1对y做了分类,根据x2对y做了分类,做了分类之后,通过x1把y分成了两堆,一堆我们称呼其为m_left, 另外一堆我们称呼其为m_right,然后我们来定义一个loss函数:
l o s s = m l e f t n ⋅ G l e f t + m r i g h t m ⋅ G r i g h t \begin{align*} loss = \frac{m_{left}}{n} \cdot G_{left} + \frac{m_{right}}{m} \cdot G_{right} \end{align*} loss=nmleft⋅Gleft+mmright⋅Gright
现在要让这个loss函数的值最小。在整个式子中,G代表的是纯度函数,这个纯度函数可以是Entropy,也可以是Gini。
loss函数的值最小的时候,就可以实现左右两边分的很均匀。我们把这个算法就叫做CART。

CART算法其实就是classification and regression tree Algorithm, 也称为「分类和回归树算法」。
上面我们讲的所有内容可以实现分类问题,那么回归问题怎么解决呢?CART里可是包含了Regression的。
好,还是我们最之前给的数据,我们现在的y不是[0,0,1,0,1]了,我们将其更改为[1.3,1.4,0.5,0.8,1.9]。我们人类大脑中的直觉会怎么分类?会将[1.3,1.4,1.9]分为一类,而[0.5,0.8]分为一类对吧?(我说的是大部分人,少部分「天才」忽略)。
那么为了完成这样的一个分类,我们将之前公式里的纯度函数替换成MSE,那么函数就会变成如下这个样子:
J ( k , t k ) = m l e f t m ⋅ M S E l e f t + m r i g h t m M S E r i g h t J(k, t_k) = \frac{m_{left}}{m} \cdot MSE_{left} + \frac{m_{right}}{m}MSE_{right} J(k,tk)=mmleft⋅MSEleft+mmrightMSEright
MSE是什么呢?其实就是均方误差。
M S E n o d e = ∑ i ∈ n o d e ( y ^ n o d e − y ( i ) ) 2 y ^ n o d e = 1 m n o d e ∑ i ∈ n o d e y ( i ) \begin{align*} MSE_{node} & = \sum_{i \in node}(\hat y_{node} - y^{(i)})^2 \\ \hat y_{node} & = \frac{1}{m_{node}}\sum_{i\in node}y^{(i)} \end{align*} MSEnodey^node=i∈node∑(y^node−y(i))2=mnode1i∈node∑y(i)
我们要取的,就是最小的那一个MSE。
决策树最大的优点就是在决策上我们需要更大的解释性的时候很直观,决策树可以将其分析过程以树的形式展现出来。一般在商业、金融上进行决策的时候我们都需要很高的解释性。就比如下面这个例子:
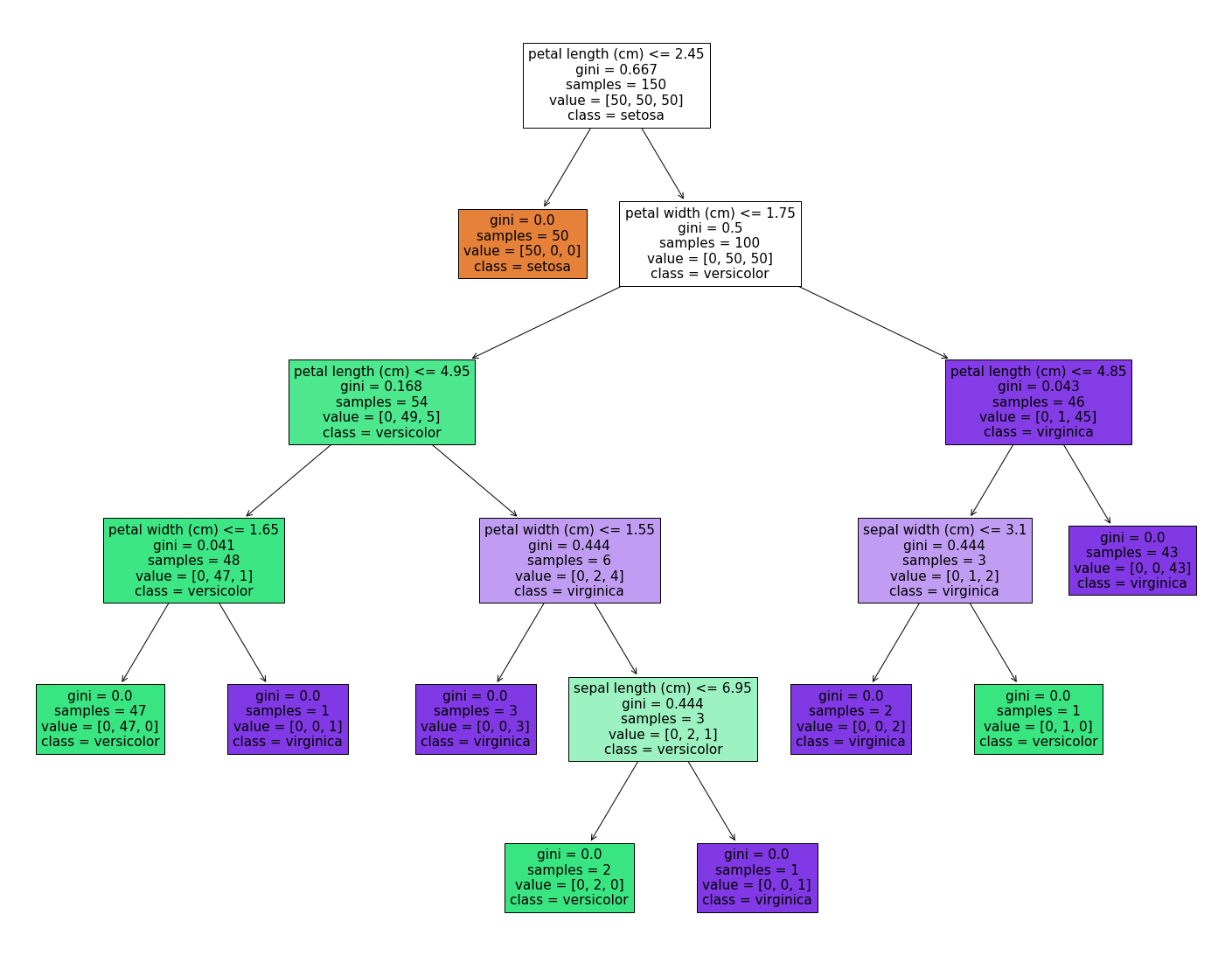
第二呢,它可以来提取重要特征。决策术可能某一类问题上效果假设最多只能做到85%的准确度,我们期望换一种模型,希望用到的维度少一点。
比方说要做逻辑回归,我们期望的w.x+b乘以一个Sigmoid,原来的x是10维的,我们期望把它降到5维。那这个时候决策树的构建过程就从最显著的特征开始逐渐构建,我们就可以把它前五个特征给他保留下来,前五个特征就是最salience的feature。我们假如把它用到逻辑回归上,直接用这五个维度就可以了。
接着我们来个问题:本来是10维的我们期望把它变成5维,为什么我们希望降维呢?
还记得我们「拟合」这一节么?我们说过,过拟合最主要的原因是数据量过少或者模型过于复杂,那为什么数据量过少呢?不知道是否还记得我讲过的维度灾难。
多个维度就需要多个数量级的数据。在仅有这么多数据的情况下,维度越多需要更多数据来拟合,但是大部分时候我们并没有那么多数据。
这个问题其实是一个很经典的问题,为什么我们做各种机器学习的时候期望降维。如果能把这个仔仔细细的想清楚,其实机器学习原理基本上已经能够掌握清楚了。
接下来我们再说说它的缺点,其实也很明显,它的分类规则太过于简单。所以它最大的缺点就是因为简单,所以好解释,但正是因为简单,所以解决不了复杂问题。
和SVM一样,也可以给决策树加核函数,曾经有一段时间这也是很重要的一个研究领域。
好,在结束之前我们预告一下下一节课内容,我们还是讲决策树,讲讲决策树中的Adaboost等,以及决策树的升级版:随机森林。
相关文章:

16. 机器学习 - 决策树
Hi,你好。我是茶桁。 在上一节课讲SVM之后,再给大家将一个新的分类模型「决策树」。我们直接开始正题。 决策树 我们从一个例子开始,来看下面这张图: 假设我们的x1 ~ x4是特征,y是最终的决定,打比方说是…...

将多余的内存,当作虚拟内存。修改edge缓存路径到虚拟内存中
一、下载工具,把内存映射成硬盘 软媒内存盘 v1.1.3.0 软媒内存盘下载-软媒内存盘 v1.1.3.0 - 下载吧 (xiazaiba.com) 二、映射edge的缓存路径 到新建的虚拟硬盘中 mklink /D "C:\Users\Administrator\AppData\Local\Microsoft\Edge\User Data" "V:\…...

【从0到1设计一个网关】过滤器链的实现---实现负载均衡过滤器
文章目录 什么是过滤器?编写负载均衡过滤器负载均衡的定义与实现负载均衡算法设计实现效果演示链接 自研网关整合Nacos,实现服务注册和配置变更 源码链接 什么是过滤器? 再前面的几个章节中我们已经实现了将我们的网关服务注册到注册中心,并且成功的从配置中心拉取了配置…...

科技云报道:打造生成式AI应用,什么才是关键?
科技云报道原创。 生成式AI作为当前人工智能的前沿领域,全球多家科技企业都在加大生成式AI的研发投入力度。 随着技术、产品及应用等方面不断推出重要成果,如今有更多的行业用户在思考该如何将生成式AI应用落地。 但开发生成式AI应用是一个充满挑战的…...

可回馈式电子负载的工作原理
可回馈式电子负载是一种用于模拟负载并测试电源或电子设备性能的工具。其工作原理如下: 控制回路:可回馈式电子负载内部有一个控制回路,用于监测和控制负载的电流、电压和功率等参数。这个控制回路可以根据用户设定的参数,自动调整…...
基于Vite使用VitePress搭建静态站点博客
使用VitePress搭建静态站点博客 官方文档什么是VitePress?一、初始化项目1.安装依赖包VitePress可以单独使用,也可以安装到现有的项目中。在这两种情况下,您都可以安装它: (也可以全局安装,建议:当前项目内安装) 2.初始…...

湖南互联网医院-让患者随时随地接受医疗服务
打造移动互联网医院,就是,通过移动互联网将医院与患者、医院内部(医生、护士、领导层)、医院与生态链上的各类组织机构连接起来。以患者为中心,优化医院业务流程,提升医疗服务质量与医院资源能效࿰…...
【建议收藏】免费体验的AI论文写作网站-「智元兔 AI」
在当今技术飞速发展的时代,越来越多的领域开始应用人工智能(Artificial Intelligence,简称AI)。其中,AI写作工具备受瞩目,备受推崇。 在众多的选择中,智元兔AI是一款在笔者使用过程中非常有帮助…...
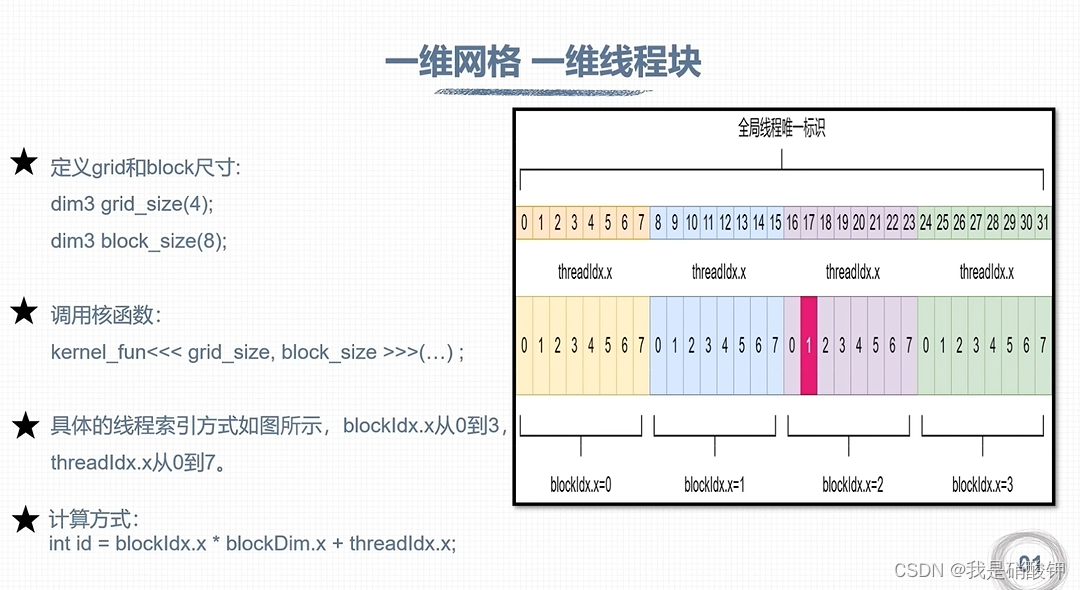
CUDA编程
线程全局索引计算方式 一维网格和一维的线程块 计算方法:...

gorilla/websocket的chat示例代码简单分析
代码地址:https://github.com/gorilla/websocket/tree/main/examples/chat 文件包含:main.go、hub.go、client.go、home.html main.go文件 func main() {flag.Parse()hub : newHub() // 实例化Hubgo hub.run() // 使用chan处理 增删Hub的连接 和 广播消…...

地图坐标展示工具folium
参考:https://github.com/python-visualization/folium https://zhuanlan.zhihu.com/p/384078185?utm_id0 https://www.w3cschool.cn/article/37568875.html 其他还有baidu:echarts 安装: pip install folium代码(离线地图&a…...

Ruby 之方法委托
ruby 方法委托的优点在于,可以将多个不同实例(或类)的方法组织在一起,然后进行统一调用,方便各类方法的统一管理。比如下边示例中的 color 和 username,本来是不同类里边的方法,但最后都可以统一…...
[论文笔记]RetroMAE
引言 RetroMAE,中文题目为 通过掩码自编码器预训练面向检索的语言模型。 尽管现在已经在许多重要的自然语言处理任务上进行了预训练,但对于密集检索来说,仍然需要探索有效的预训练策略。 本篇工作,作者提出RetroMAE,一个新的基于掩码自编码器(Masked Auto-Encoder,MAE)…...

服务熔断保护实践--Sentinal
目录 概述 环境说明 步骤 Sentinel服务端 Sentinel客户端 依赖 在客户端配置sentinel参数 测试 保护规则设置 设置资源名 设置默认的熔断规则 RestTemplate的流控规则 Feign的流控规则 概述 微服务有很多互相调用的服务,构成一系列的调用链路…...

页面淘汰算法模拟实现与比较
1.实验目标 利用标准C 语言,编程设计与实现最佳淘汰算法、先进先出淘汰算法、最近最久未使用淘汰算法、简单 Clock 淘汰算法及改进型 Clock 淘汰算法,并随机发生页面访问序列开展有关算法的测试及性能比较。 2.算法描述 1. 最佳淘汰算法(Op…...

FPGA实现HDMI转LVDS视频输出,纯verilog代码驱动,提供4套工程源码和技术支持
目录 1、前言免责声明 2、目前我这里已有的图像处理方案3、本 LVDS 方案的特点4、详细设计方案设计原理框图视频源选择静态彩条IT6802解码芯片配置及采集ADV7611解码芯片配置及采集silicon9011解码芯片配置及采集纯verilog的HDMI 解码模块奇偶场分离并串转换LVDS驱动 5、vivado…...

JAVA-easyexcel多sheet页导入
今天给宝子带来一套多sheet页导入的模板,话不多说直接上代码 String localFilePath "file.xlsx";JSONObject jsonObject JSON.parseObject(file);String useFile jsonObject.getString("file");useFileuseFile.replace("\\\\",&qu…...
)
Java——比较器(一文搞懂比较器Comparable和Comparator)
基于Comparable的接口类基于Comparator的接口类 1、比较器的Comparable接口类 Comparable类的定义: public interface Comparable<T>{ public int compareTo(T o); }2、Comparable比较器的返回值: 此方法返回一个int类型的数据,但是此int的值…...

企业直播招聘抖音报白如何实现?怎么样才能报白成功?
现在每天几亿人都在使用抖音等短视频平台进行娱乐或者工作学习,也有很多商家和企业利用抖音等短视频平台进行盈利和企业宣传相关的服务,其中比较典型的就是通过抖音直播等功能为自身企业进行招聘。 但是通过抖音等短视频平台进行招聘时,很多…...

【考研数学】概率论与数理统计 —— 第七章 | 参数估计(2,参数估计量的评价、正态总体的区间估计)
文章目录 一、参数估计量的评价标准1.1 无偏性1.2 有效性1.3 一致性 二、一个正态总体参数的双侧区间估计2.1 对参数 μ \mu μ 的双侧区间估计 三、一个正态总体的单侧置信区间四、两个正态总体的双侧置信区间写在最后 一、参数估计量的评价标准 1.1 无偏性 设 X X X 为总…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
