动态规划算法实现------转换(编辑、变换)问题
目录
一、字符串转换问题
1.1问题
1.2确定动态规则(DP、状态转移方程)、初始值
(1)插入操作实现状态转移
(2)删除操作实现状态转移
(3)替换操作实现状态转移
(4)初始值
1.3动态规划算法代码实现
(1)完整代码
(2)程序速度优化
二、矩阵变换问题
2.1问题
2.2矩阵乘法
(1)矩阵相乘的条件
(2)矩阵乘法原理
(3)矩阵乘法符合结合律
(4)两个矩阵相乘的乘法运算个数(次数)
(5)结合律下的多个矩阵相乘的乘法运算个数(次数)
(6)多个矩阵连乘所得矩阵的行、列数
2.3确定动态规则(DP、状态转移方程)
1、子状态空间与子状态
2、动态规则(DP、状态转移方程)
2.4确定初始值
2.5状态转移的因素
2.6动态规划算法代码实现
动态规划算法实现------转换(编辑、变换)问题
一、字符串转换问题
1.1问题
编辑距离(Edit Distance),又叫Levenshtein距离(Levenshtein Distance),对于两个字符串(或单词),把一个字符串转换成另一个字符串所需的最少操作次数。
1.2确定动态规则(DP、状态转移方程)、初始值
记A=’kitten’,B=’ sitting’,求A字符串转换成B字符串需要的最少操作次数。一个字符串转换为另一个字符串有三种操作:插入(Insertion)、删除(Deletion)、替换(Substitution)。
A转换成B,对于计算机来讲,比较适合依靠循环逐步把A中的字符转换成与B匹配成功的字符,在这个过程中使用插入、删除或替换操作来实现,比如:A中’k’转换成B中’s’, A中’k’转换成B中’i’,…,A中’i’转换为B中’s’, A中’i’转换为B中’i’,…,类似这样逐个依靠循环实现,显然这与人直接判断哪些位置需要修改是有区别的,若让人修改,直接把首尾改动即可,我们也可以让计算机做这种修改,但这种方式只能解决一种情形,不能推广到其它情形,不适合题目的普遍性的求解问题。既然计算机更适合这种逐步的判断,我们的算法必须也要符合这种计算特点,而且算法应该适合普遍性,这样的算法才有泛化能力。我们需要找到一种普遍的规律,适合计算机对所有字符串之间的转换。
这种操作是依靠循环来实现的,一般是在循环的索引所到的位置进行插入、删除和替换的操作,而不是随意的位置进行这三个操作。在计算机循环判断中,把一个字符串转换成另一个字符串,就是通过插入、删除或替换来改变前者,最后与后者长度一致,且对应位置的字符相同。下面的分析也实际是基于计算机的这些特点来描述的。
A[0:i]表示字符串A的前i个字符构成的局部字符串,B[0:j] 表示字符串B的前j个字符构成的局部字符串。在计算过程中i,j是随着循环而取值的,我们可以记dp[i][j]是把A[0:i]转换为B[0:j] 所需的最少操作次数,i,j取到当A[0:i]、B[0:j]分别代表各自整个字符串时,就是最终状态,这也是我们要所求的问题。dp[i][j]可以看作是第ij状态的值。由于下面第ij状态是唯一的,不是多个状态,为了方便表述,把第ij状态也称为dp[i][j]状态,严格来讲,两者应该区分开,特别在有的动态规划中第ij状态有多个子状态时,应该区分开,这样概念更清晰。
在本例中,插入、删除或替换是实现状态的方式,这三种方式决定了当前状态dp[i][j]是由直接相关的三个状态dp[i][j-1]、dp[i-1][j]、dp[i-1][j-1]参与计算。
dp[i][j]的计算与直接相关状态有关。在本例中,插入、删除或替换是实现状态的方式,这三种方式决定了当前状态dp[i][j]的直接相关的三个状态为dp[i][j-1]、dp[i-1][j]、dp[i-1][j-1]。插入对应了对dp[i][j-1]状态的操作,删除对应了对dp[i-1][j]状态的操作,替换对应了对dp[i-1][j-1]状态的操作。
从一个状态到另一个状态都是靠插入、删除或替换中任何一个来实现的。dp[i][j]与直接相关状态有关,它的已产生的直接相关状态有dp[i][j-1]、dp[i-1][j]、dp[i-1][j-1],而达到某个状态都是靠插入、删除或替换来实现的。
(1)插入操作实现状态转移
插入操作实现状态转移,dp[i][j]状态只能是由dp[i][j-1]转移过来。由 dp[i][j-1]到dp[i][j]状态,i不变,而j-1到j增加了一个字符,说明状态转移中,A[0:i]的长度不变,而B[0:j]字符窜长度增加了1,因而只能插入操作,才有它们的长度可能一致且出现最佳情况:在A[0:i]末尾插入一个字符就实现了dp[i][j]状态下与B[0:j]转换成功。因此,由dp[i][j-1]状态到dp[i][j]状态最少操作次数是dp[i][j]=dp[i][j-1]+1,其它删除或替换操作都会大于这个次数。
(2)删除操作实现状态转移
删除操作实现状态转移,dp[i][j]状态只能是由dp[i-1][j]转移过来。由 dp[i-1][j]到dp[i][j]状态, i-1变成了i,而j不变,说明状态转移中,A[1:i]的长度增加了1,而B[0:j]字符窜长度不变,因而只能删除操作,才有它们的长度可能一致且出现最佳情况:删除A[0:i]末尾一个字符就实现了dp[i][j]状态下与B[0:j]转换成功。因此,由dp[i-1][j]状态到dp[i][j]状态最少操作次数是dp[i][j]=dp[i-1][j]+1,其它插入或替换操作都会大于这个次数。
(3)替换操作实现状态转移
替换操作实现状态转移,dp[i][j]状态只能是由dp[i-1][j-1]转移过来。由 dp[i-1][j-1]到dp[i][j]状态, i-1变成了i,而j-1变成了j,两者都是增加1,说明状态转移中,A[0:i]、B[0:j]的长度在原来基础上都增加了1,因而只能替换操作,它们的长度可能一致且出现最佳情况:替换A[0:i]末尾一个字符就实现了dp[i][j]状态下与B[0:j]转换成功,当A[0:i]中的字符A[i]与B[0:j]中的字符B[j]不相同时,A[i]需要被替换为B[j],dp[i][j]= dp[i-1][j-1]+1,但当A[i]与B[j]相同时,不需要替换,此时,dp[i][j]= dp[i-1][j-1],其它插入或删除操作都会大于这个次数。
dp[i][j]可以由上述三个直接相关状态之一转化而来,因而可以取三个直接相关状态中的最小值min,即为我们所需的最少转换操作次数。上面的描述内容也即是普通情况下的动态规则DP,根据这个DP,我们可以计算出新的状态。
(4)初始值
下面我们再来确定初始状态。初始状态的源头是空字符转换为非空字符,若A为空字符,B不是空字符,A转换为B[0:j],用0表示空字符的索引,也即表示初始状态的情形,显然,dp[0][j]=j,相当于不断的插入字符,j为插入字符的个数;若A为非空字符,B为空字符,A[0:i] 转换为B,显然,dp[i][0]=i,相当于不断的删除字符,i为删除字符的个数。当然,我们可以把初始状态从1个字符开始,显然,没有从空字符手动计算方便,初始值一般是手动计算的。
本例中的初始状态是一种特别情况,需要单独处理,我们可以把初始值和上面的普遍情况统一为下面动态规则DP(状态转移方程):

简化为:

上面简化的数学表达式中,①式可以看作是问题的特别情况,单独处理,②式可以看作是问题的普通情况,也即为动态规则DP(也即状态方程)。
前面我们是从字符串A、B都不为空进行分析,dp[i][j]的索引与字符串的索引是一致的,这种不影响分析,但现在加上刚才增加了空字符这种初始状态,要注意dp[i][j]的索引变成比字符串的索引多一个,如图2-5所示。因此,在代码中注意i、j索引表达的变化,否则,使用不当容易产生异常提示string index out of range。
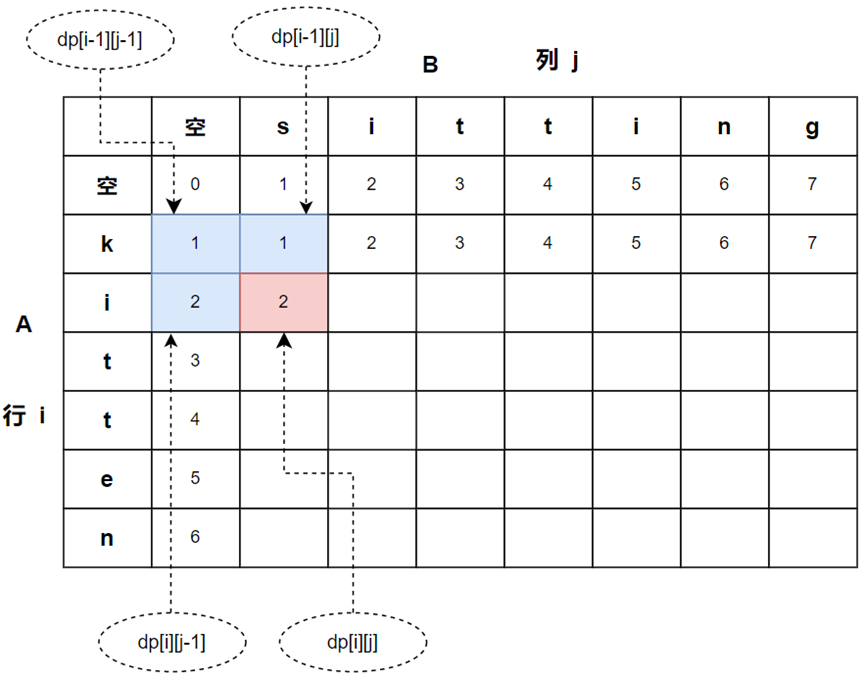
图2-5 编辑距离最少操作次数
上面的分析及下面代码的实现可以结合下面图2-5来理解。红色区域的状态由周围蓝色的状态决定,即’ki’转换成’s’至少需要操作2次。下面程序代码是实现编辑问题。
1.3动态规划算法代码实现
(1)完整代码
下面代码是按上述分析过程实现的,完全体现了我们上面对动态规划的论述,从代码中就能看到动态规划算法的思想,我们可以结合下面代码来理解动态规划算法在本问题中的应用。
#编辑距离问题
def edit_distance(A, B):#增加1,因为初始值增加了空字符有关的行列。n, m = len(A) + 1, len(B) + 1#生成一个二层列表,存放状态值。dp= [[0] * m for i in range(n)]#初始值,本例中初始值实际对应为特别情况。#dp[0][0] = 0#定义列表时已赋值。for i in range(1, n):#空字符的处理dp[i][0] = i #也即dp[i][0]=dp[i - 1][0] + 1for j in range(1, m):#空字符的处理dp[0][j] = j#也即dp[0][j]=dp[0][j - 1] + 1#普通情况,这里的i,j索引是dp的索引,0表示空字符,因此,索引从1开始。for i in range(1, n):for j in range(1,m):#下面要注意A、B的索引值,它们的索引不是dp对应的索引值,要减去1,才刚好对应。#因为字符串的索引是从0开始,所以字符串中减去1,当dp到i,j时,由于上面增加了空字符处理的行和列,#所以A[i - 1],B[j - 1]刚好是对应了当前状态dp[i][j]。if A[i - 1] == B[j - 1]:temp = 0else:temp = 1dp[i][j] = min(dp[i-1][j]+ 1,dp[i][j-1]+1,dp[i-1][j-1]+temp)#动态规则(DP)# dp逐行输出for i in range(n):print(dp[i])return dp[- 1][- 1]ed = edit_distance('ki相关文章:

动态规划算法实现------转换(编辑、变换)问题
目录 一、字符串转换问题 1.1问题 1.2确定动态规则(DP、状态转移方程)、初始值 (1)插入操作实现状态转移 (2)删除操作实现状态转移 (3)替换操作实现状态转移 (4)初始值 1.3动态规划算法代码实现 (1)完整代码 (2)程序速度优化 二、矩阵变换问题 2.1问题 2.2矩阵乘法 (1)矩阵相乘…...

C#使用Oracle.ManagedDataAccess.dll
1、添加引用 在网上下载一个Oracle.ManagedDataAccess.dll,引用即可,视操作系统的位数,最重要的是减少了Oracle客户端的安装; 2、web.config字串 <appSettings> <add key"hrp" value"Data Source (…...

分享88个工作总结PPT,总有一款适合您
分享88个工作总结PPT,总有一款适合您 88个工作总结PPT下载链接:https://pan.baidu.com/s/1y08X9RMdIOCncbs28aMgDw?pwd8888 提取码:8888 Python采集代码下载链接:采集代码.zip - 蓝奏云 蓝色水彩风年终总结PPT模板 清新水彩简…...

【华为OD题库-002】最佳植树距离-Java
题目 小明在直线的公路上种树,现在给定可以种树的坑位的数星和位置,以及需要种多少棵树苗,问树苗之间的最小间距是多少时,可以保证种的最均匀(两棵树苗之间的最小间距最大) 输入描述 输入三行: 第一行一个整数:坑位的数…...

【python与数据结构】(leetcode算法预备知识)
笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~ python与数据结构 Python 中常见的数据类型数据结构1.数组(Array)2.链表(Linked List)3.哈希表(Hash Table)4.队列(Queue&#x…...

前端+Python实现Live2D虚拟直播姬
写在前面 很早就在b站上看到有虚拟主播的方案,之前看到的方案主要分为3种: ①用的unity+live2d②有的用的steam的Vtube Studio这款软件③也有基于galgame的。基于纯前端和python的我好像没找到,在掘金看到一篇文章:juejin.cn/post/720474… ,使用的pixi-live2d-display这…...

华纳云 宝塔怎么配置香港服务器多ip?
宝塔面板是一款开源的服务器管理面板,提供了简单易用的图形化界面,使用户能够轻松管理和配置服务器。通过切换到香港服务器多IP,用户可以拥有更多的IP资源,提供更灵活的网络服务。 配置香港服务器多IP 1.登录宝塔面板 打开浏览器&…...

云计算是什么
一文读懂云计算:发展历程、概念技术与现状分析 - 知乎 “现阶段所说的云计算,已经不单单是一种分布式计算,而是分布式计算、效用计算、负载均衡、并行计算、网络存储、热备份冗杂和虚拟化等计算机技术混合演进并跃升的结果。” 云计算的关键…...
【POI-EXCEL-下拉框】POI导出excel下拉框数据太多导致下拉框不显示BUG修复
RT 最近在线上遇到一个很难受的BUG,我一度以为是我代码逻辑出了问题,用了Arthas定位分析之后,开始坚定了信心:大概率是POI的API有问题,比如写入数据过多。 PS:上图为正常的下拉框。但是,当下拉…...
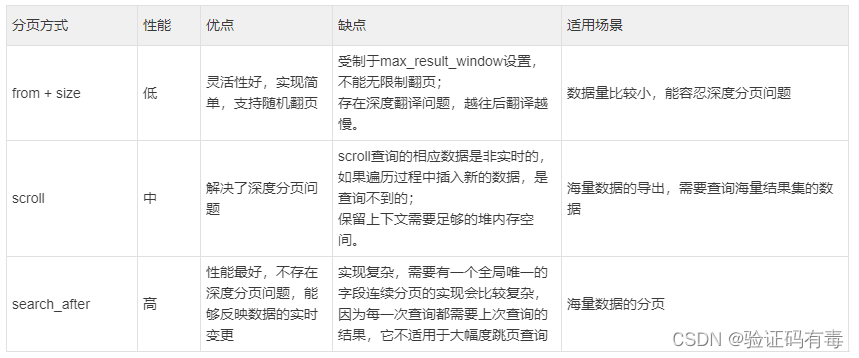
【ES专题】ElasticSearch 高级查询语法Query DSL实战
目录 前言阅读对象阅读导航前置知识数据准备笔记正文一、ES高级查询Query DSL1.1 基本介绍1.2 简单查询之——match-all(匹配所有)1.2.1 返回源数据_source1.2.2 返回指定条数size1.2.3 分页查询from&size1.2.4 指定字段排序sort 1.3 简单查询之——…...

陕西某小型水库雨水情测报及大坝安全监测项目案例
项目背景 根据《陕西省小型病险水库除险加固项目管理办法》、《陕西省小型水库雨水情测报和大坝安全监测设施建设与运行管理办法》的要求,为保障水库安全运行,对全省小型病险水库除险加固,建设完善雨水情测报、监测预警、防汛道路、通讯设备、…...

pte rs练习方法 请介绍一下crank请介绍一下sanctuary请介绍一下solitary请介绍一下coarse请介绍一下deception
目录 pte rs练习方法 请介绍一下crank 请介绍一下sanctuary 请介绍一下solitary 请介绍一下coarse 请介绍一下deception pte rs练习方法 请介绍一下crank “Crank”一词可以个指不同的事物,具体含义视上下文而定。在不同的领域,这个词有不同的解…...
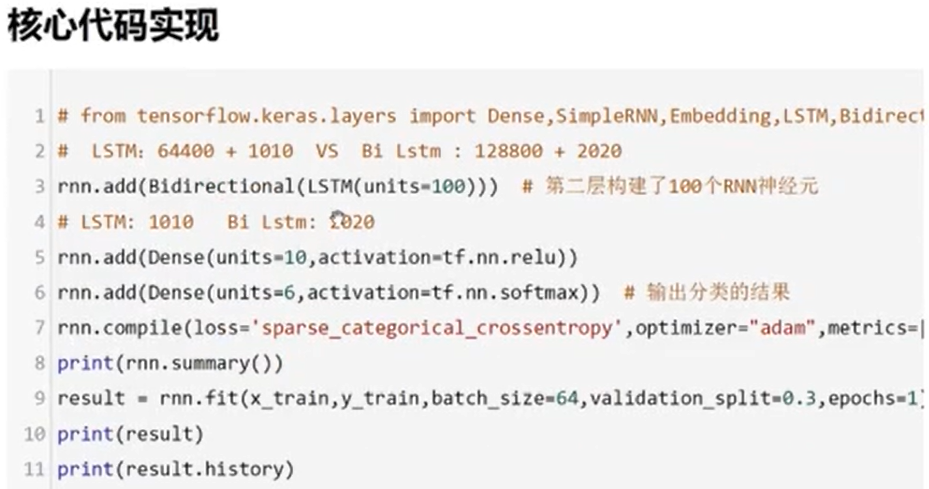
NLP之LSTM与BiLSTM
文章目录 代码展示代码解读双向LSTM介绍(BiLSTM) 代码展示 import pandas as pd import tensorflow as tf tf.random.set_seed(1) df pd.read_csv("../data/Clothing Reviews.csv") print(df.info())df[Review Text] df[Review Text].astyp…...

【实现多个接口的使用】
文章目录 前言实现多个接口接口间的继承接口使用实例给对象数组排序创建一个比较器 总结 前言 实现多个接口 Java中不支持多继承,但是一个类可以实现多个接口 下面是自己反复理了很久才敲出来的,涉及到之前学的很多知识点 如果哪看不懂,真…...

Mac收集的几个终端命令
文章目录 转UTF-8编码格式打tag 包 命令:压缩加密文件显示隐藏文件取消Mac电脑安全模式 转UTF-8编码格式 cd到目录下 iconv -f gbk -t utf-8 gbk.txt > utf8.txt打tag 包 命令: cd到目录下 tar -cvf demo.tar.gz demo a demo压缩加密文件 cd 到文…...
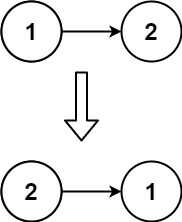
206. 反转链表、Leetcode的Python实现
博客主页:🏆看看是李XX还是李歘歘 🏆 🌺每天分享一些包括但不限于计算机基础、算法等相关的知识点🌺 💗点关注不迷路,总有一些📖知识点📖是你想要的💗 ⛽️今…...

VS2022 打包WPF安装程序最新教程(图文详解)
文章目录 前言一、安装打包Installer插件1、单独安装2、VS中在线安装二、使用步骤1、创建安装项目2、安装项目主界面3、添加项目输出4、添加快捷方式图标5、添加卸载项目a、新建项目b、添加项目输出c、创建快捷方式6、给快捷方式添加图标a、在Resource文件夹中添加图标文件b、选…...

清华大模型GLM
2022年,清华大学发布了一款具有重要意义的 GLM 大模型,它不仅在中文语言处理方面取得了显著的进展,还在英文语言处理方面表现出了强大的能力。GLM大模型区别于OpenAI GPT在线大模型只能通过API方式获取在线支持的窘境,GLM大模型属于开源大模型,可以本地部署进行行业微调、…...
实时数仓-hologres使用总结
我们回顾下,Hologres是一款实时HSAP产品,隶属阿里自研大数据品牌MaxCompute,兼容 PostgreSQL 生态、支持MaxCompute数据直接查询,支持实时写入实时查询,实时离线联邦分析,低成本、高时效、快速构筑企业实时…...

博客摘录「 TCP/IP网络编程——习题答案」2023年10月29日
clnt_sdaccept(serv_sd, (struct sockaddr*)&clnt_adr, &clnt_adr_sz);read(clnt_sd, file_name, BUF_SIZE); fpfopen(file_name, "rb"); //尝试打开客户端请求的文件if(fp!NULL) //如果文件存在,则传送给客户端{while(…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
