如何估计池塘里鱼的数目,周边有多少车辆?
如何估计池塘里鱼的数目?
老李想估计一下自己池塘里鱼的数量,第一天他捕捞了50条鱼做好标记,然后全放回池塘。过了几天带标记的鱼完全混合于鱼群中,他又去捕捞了168条,发现做标记的鱼有8条。帮老李估算一下池塘里的鱼有多少条。
这是一个典型的用抽样样本来估计总体的统计办法。168条鱼中有8条标记鱼,这样老李可以估计标记鱼占全体鱼的比是8:168。由于总共有50条标记鱼,那么全体鱼的数目就应该是1050。
50×168÷8=1050
简单估计池塘里的鱼群的数目容易产生较大的误差,如果偶然只捞了两条标记鱼,那么池塘里鱼的总数就会被高估,50×168÷6=1400条!这样很轻易就造成了25%的误差。
减少误差的方法
基于这个原因,如果这些鱼经得起折腾的话,更好的办法是放回去再多捕捞几次,取个平均值。
先从池塘中捞出100条鱼分别做上记号,放回池塘,等鱼完全混合后,第一次捞出100条鱼,其中有4条带标记的鱼,第二次又捞出100条鱼,其中有6条带标记的鱼。 100 x = 4 + 6 100 + 100 \frac{100} {x}=\frac{4+6}{100+100} x100=100+1004+6,则, x = 2000 x=2000 x=2000。
正态分布近似估算
这是一种基于二项分布理论的方法,但在这里可用正态分布近似估算。计算误差时,只需改变样本方差的算法即可,其他都不变。以《数据化决策》书中的案例为例。
N = p ± z a 2 p ( 1 − p ) n N=p±z_{\frac{a}{2}}\sqrt{\frac{p(1-p)}{n}} N=p±z2anp(1−p)
其中:
p p p,样本比例。
z a 2 z_{\frac{a}{2}} z2a,置信区间统计量,例如95%置信区间取1.96,90%取1.645。
n n n,样本数量。
标准误差(standard error)通常是指样本统计量(如样本平均值、样本标准差等)的标准差,它反映了统计量的抽样误差。标准误差的计算公式与具体的统计量相关。
统计量的标准误差,当总体标准差未知时,可用样本标准差代替计算,这时计算的标准误差称为估计标准误差(standard error of estimation)。由于实际应用中,总体总是未知的,所计算的标准误差实际上都是估计标准误差,因此估计标准误差就简称为标准误差。同样,当总体比例的方差未知时,可用样本比例的方差代替。计算公式: p ( 1 − p ) n \sqrt{\frac{p(1-p)}{n}} np(1−p)。
先从池塘中捞出1000条鱼分别做上记号,放回池塘,等鱼完全混合后,再捞出1000条鱼,其中有50条是做过标记的,这就意味着池塘里大概有5%的鱼做过标记,因此,得出结论是池塘里大约有20000条鱼。
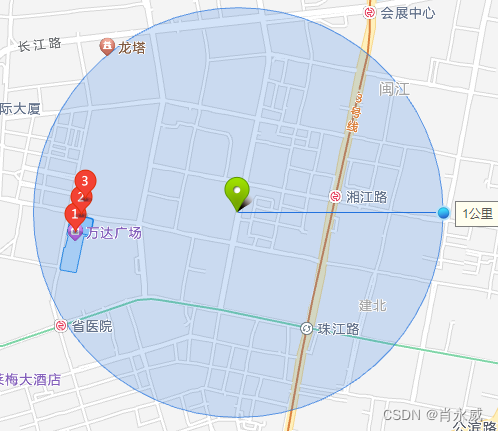
样本方差是用群体内的样本比例乘以非样本比例。换句话说,是将二次抓取时鱼群中做标记的比例(0.05)乘以没做标记的比例(0.95),结果是 0.05 × 0.95 = 0.0475 0.05\times0.95=0.0475 0.05×0.95=0.0475,按90%置信区间取1.645。
1.645 0.0475 1000 = 0.012 1.645\sqrt{\frac{0.0475}{1000}}=0.012 1.64510000.0475=0.012
0.05 ± 0.012 = ( 3.8 % ∼ 6.2 % ) 0.05±0.012=(3.8\% \sim6.2\%) 0.05±0.012=(3.8%∼6.2%)
因此湖中鱼的总数是16129~26316,(1000/0.062=16129,1000/0.038=26316)。
对有些人来说,这看似是一个比较大的范围,但假设我们以前的不确定性水平很高,校准估计的范围也只是2000~50000条,所以这一范围已经大为缩小了。如果我们当初放养了5000条鱼,现在仅仅是想知道鱼的总数是增加了还是减少了,那么任何大于6000的数字都表示鱼的总数增加了,超过10000条当然更好。如果把初始范围和相关阈值都考虑在内,不确定性显然已经大为减小,误差也在可接受范围之内。实际上,我们完全可以在第一次抓捕中只抓250条鱼,然后放掉,再抓250条,也就是说抽样量只有前面的1/4。假设做过标记的鱼在第2次重抓时所占比例也是5%左右,那么我们对鱼的总数超过6000条仍然很有信心,也就是说6000仍然在90%置信区间内。
这种通过抽样来揭示全貌的方法特别有用,这种方法已经用于评估美国人口普查局统计遗漏的人数、亚马孙流域未经发现的蝴蝶种类及未知的潜在顾客数量等问题。未能看到整体全貌,并不意味着不能对它进行量化。
从本质上说,抓与重抓是两次独立抽样,比较两次抽样的重合程度,可以估计群体总数。
周边有多少车辆应用思考?
如果我们想知道我们生活的区域周边有多少车辆,可否使用这样方案。
例如,我们在纵向的街道上,通过随机录像、拍照记录1000辆车牌号,下周大致相同时间,再随机记录1000辆车牌号;同样方法在横向街道,再进行一次,这样估算反映了什么呢?
反映出这个街道上,周边能到此街道的车辆规模,是这样吗?
怎么抽样更准?
抽样占比为5%,样本数分别为100、1000、1000,则整体估计情况如下:
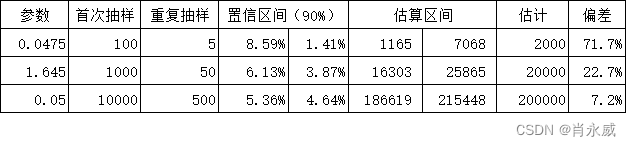
重复抽样标记比例提高到10%,其他不变则整体估计情况如下:
怎么抽样更准?
首先是增大样本数,其次,在样本数不变的情况下,尽量提高标记比例。
参考:
Douglas W. Hubbard. 数据化决策. 广东人民出版社. 2018.05
相关文章:

如何估计池塘里鱼的数目,周边有多少车辆?
如何估计池塘里鱼的数目? 老李想估计一下自己池塘里鱼的数量,第一天他捕捞了50条鱼做好标记,然后全放回池塘。过了几天带标记的鱼完全混合于鱼群中,他又去捕捞了168条,发现做标记的鱼有8条。帮老李估算一下池塘里的鱼…...
docker中安装rabbitMq并配置启动
目录 1. 拉取镜像并安装(此处实例安装的是最新版)2.查看docker中已安装的镜像和版本3.启动RabbitMq4.配置管理端5.安装完成 1. 拉取镜像并安装(此处实例安装的是最新版) docker pull rabbitmq2.查看docker中已安装的镜像和版本 …...

viewfs://为Hadoop 中的一个特殊文件系统
解释 viewfs:// 是 Hadoop 中的一个特殊文件系统 URI,用于访问 Hadoop 的视图文件系统(ViewFS)。 ViewFS 是 Hadoop 提供的一种虚拟文件系统,它可以将来自多个底层文件系统的文件统一管理和访问。 通过 ViewFS,你可…...
UniPro自定义个人专属工作台 大幅提升工作效率
很多研发团队在开完每日站会后,工程师的工作习惯便是打开研发管理系统,先看看自己的待办事项,或是查看同事的需求、评论,亦或是查看今日份工作的高优先级项等等。 如何方便工程师能够快速查看和了解一天的工作究竟从哪开始呢&…...
python调用飞书机器人发送文件
当前飞书webhook机器人还不支持发送文件类型的群消息,可以申请创建一个机器人应用来实现群发送文件消息。 创建机器人后,需要开通一系列权限,然后发布。由管理员审核通过后,才可使用。 包括如下的权限,可以获取群的c…...

【产品应用】一体化伺服电机在焊接设备中的应用
随着制造业的不断发展,焊接设备在许多领域都得到了广泛应用,如汽车制造、机械加工、钢结构等领域。为了提高焊接设备的性能和效率,许多厂家开始采用一体化伺服电机作为焊接设备的主要驱动部件。本文将介绍一体化伺服电机在焊接设备中的应用背…...

uni+vue3+firstUI——组件弹框使用 v-model绑定参数
说明 将框架弹框组件 封装成子组件,在页面中引用该子组件,传参并控制弹框显示与隐藏。 子组件 <template><view><wh-modal :show"showPopup" :descr"descr" maskClosable click"onClick" :buttons"…...

【电路笔记】-正弦波形
正弦波 文章目录 正弦波1、概述2、波形产生3、总结 在 19 世纪末的 10 年间,许多技术成就使得交流电的使用得以扩展,并克服了直流电向公众供电的局限性。 1882 年,法国发明了变压器,它简化了交流电的分配,正如我们将在…...

Failed to launch task: 文件”Setup”不存在 Mac安装Adobe软件报错解决方案
在安装 Adobe 软件时,软件提示 Failed to launch task: 文件”Setup”不存在 ,这个时候怎么处理呢? 解决方法如下: 1、安装 AnitCC 或 或 Creative Cloud 环境,保证软件所需要的环境 2、如果安装后也不起作用&#x…...

什么是 DevOps
DevOps是一套融合软件开发(Dev)和 IT 运营(Ops)的实践,旨在缩短应用程序开发周期并确保以高软件质量持续交付,通过采用 DevOps 实践,您可以帮助组织更可靠、更快速、更高效地交付软件。 什么是…...
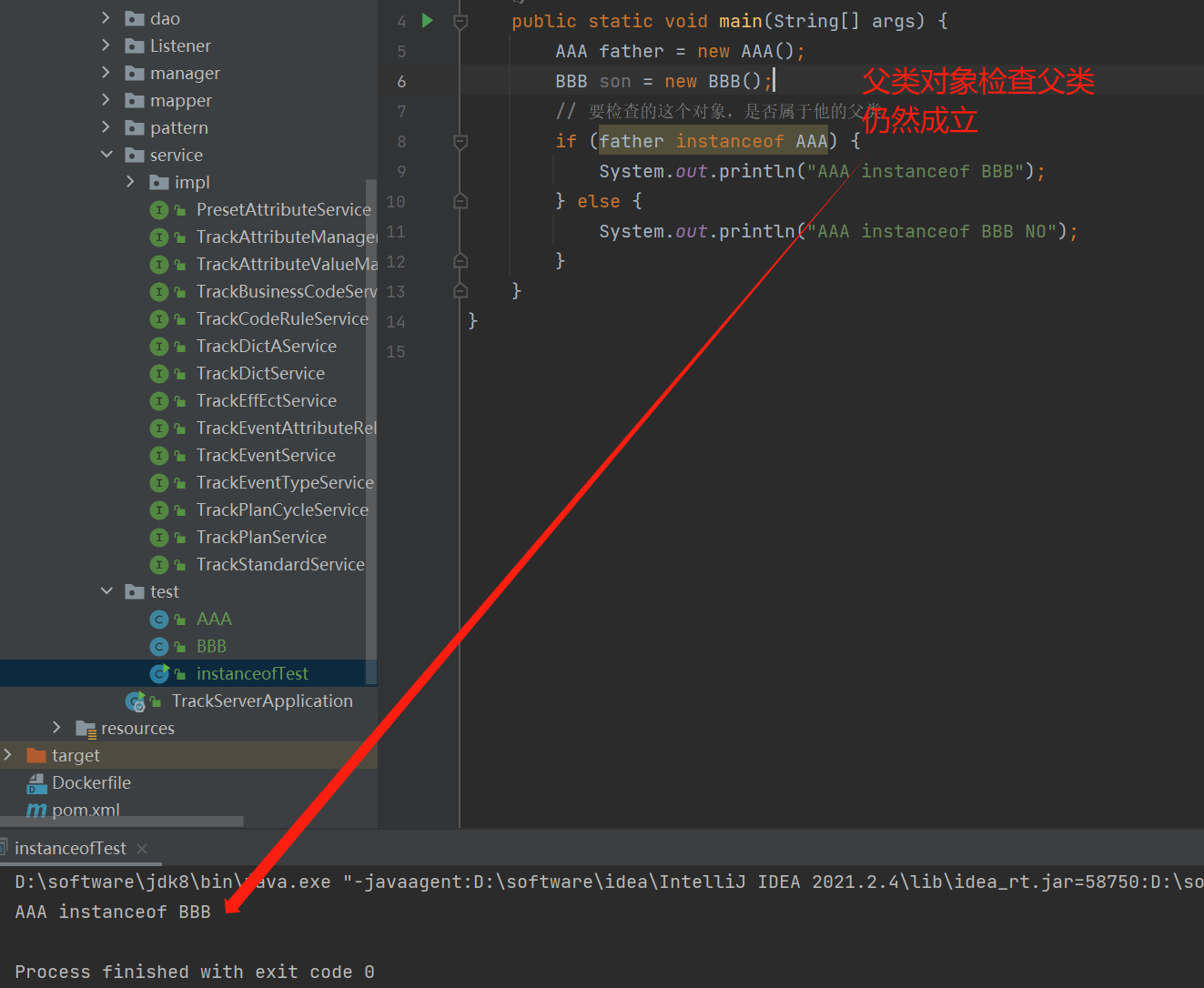
java修仙基石篇->instanceof子父类检查
instanceof检查子父类(或者是否能被强转) 作用1:检查某对象是否是某类的子类 如:儿子类继承了父亲类。 检查儿子类对象是否属于父亲类 作用2:检查两个对象是否可以强转 语法: 子类对象 instanceof 父…...

[笔记] ‘\0‘的含义:任何字符串后面都会有的结束符。
参考博客:C语言中 \0 代表什么 摘录: ‘\0’ 是字符串的结束符,任何字符串之后都会自动加上’\0’。如果字符串末尾少了‘\0’字符,则其在输出时可能会出现乱码问题。 字符串总是以“\0”作为串的结束符;因此当把一个…...

雪花算法:分布式ID生成的优雅解决方案(建议收藏)
在分布式系统中,唯一ID的生成和管理是一项重要而棘手的任务。雪花算法,由Twitter开源的一种分布式ID生成算法,为这个问题提供了一种优雅的解决方案。本文将详细介绍雪花算法的原理、设计和实现,并通过示例代码和图片帮助读者更好地…...

全国产EtherCAT运动控制边缘控制器(六):RtBasic文件下载与连续轨迹加工的Python+Qt开发
今天,正运动小助手给大家分享一下全国产EtherCAT运动控制边缘控制器ZMC432H如何使用PythonQT实现连续轨迹加工。 01 功能简介 全国产EtherCAT运动控制边缘控制器ZMC432H是正运动的一款软硬件全国产自主可控,运动控制接口兼容EtherCAT总线和脉冲型的独立…...

git代码行统计
本文介绍统计项目代码行的方式,包括使用git log统计、git ls-files统计和使用linux命令行方式统计。 一、使用git log统计 1.统计所有代码行数 当前代码都存放在git仓库下,当需进行代码行数统计时,让开发人员在代码路径下运行如下指令&…...
LEEDCODE 2235两整数相加
class Solution { public:int sum(int num1, int num2) {return (num1 num2);} };...
魔术般的速度,焕然一新的磁盘空间 - Magic Disk Cleaner for Mac 2023
在当今这个信息时代,我们的磁盘空间无时无刻不在被各种文件和数据所填满。无论是工作文件,还是日常生活的照片、视频,亦或是下载的各种应用程序,都在不断地蚕食着我们的磁盘空间。面对这种情况,一款高效、便捷的磁盘垃…...

项目切换多租户导致的数据库SQL执行异常
先贴异常日志 java.lang.reflect.InvocationTargetException at sun.reflect.NativeMethodAccessorImpl.invoke0(Native Method) at sun.reflect.NativeMethodAccessorImpl.invoke(NativeMethodAccessorImpl.java:62) at sun.reflect.DelegatingMethodAccessorImpl.invoke(D…...
安防视频监控平台EasyCVR服务器需要开启firewalld防火墙,该如何开放端口?
智能视频监控/视频云存储/集中存储/视频汇聚平台EasyCVR具备视频融合汇聚能力,作为安防视频监控综合管理平台,它支持多协议接入、多格式视频流分发,视频监控综合管理平台EasyCVR支持海量视频汇聚管理,可应用在多样化的场景上&…...
Ubuntu Desktop 20.04升级gcc-11
默认自带的gcc是9,需要升级到11 sudo add-apt-repository ppa:ubuntu-toolchain-r/test sudo apt update sudo apt install gcc-11 sudo apt install g11 sudo update-alternatives --install /usr/bin/gcc gcc /usr/bin/gcc-9 50 sudo update-alternatives -…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
