【数据结构二叉树】先序层序建立、递归非递归遍历层序遍历、树高、镜面、对称、子树、合并、目标路径、带权路径和等等
二叉树
文章目录
- 二叉树
- 1. 二叉树的建立(递归创建,结构体指针形式)
- 1.1. 先序建立
- 1.2. 层序建立
- 2. 递归遍历(结构体指针)
- 2.1. 先序遍历
- 2.2. 中序遍历
- 2.3. 后序遍历
- 3. 非递归遍历(结构体指针)
- 3.1. 层次遍历
- 3.2. 后序遍历(非递归)
- 4. 求树的高度
- 5. 中后序遍历构建
- 6. 二叉树镜面翻转
- 7. 对称二叉树
- 8. 输出所有目标路径
- 9. 判断是否为子树
- 10. 合并二叉树
- 11. 带权路径和
前言:这篇博客需要你对于二叉树有大致的了解,并且对于递归有一定的理解,懂得先序中序后序层次是啥等等,因为在这篇博客我不会对这一些概念进行讲解,我只会将我写的我看见的比较好比较简洁的代码块截下来,并不会对它进行进行过多的讲解,所以如果选择了这一篇博客,就应该做好理解透彻的准备!
1. 二叉树的建立(递归创建,结构体指针形式)
先来给出结构体:
struct Node
{char data;Node* leftchild = nullptr;Node* rightchild = nullptr;
};
1.1. 先序建立
#include<iostream>
#include<string>
using namespace std;
struct Node
{char a;Node* leftchild = nullptr;Node* rightchild = nullptr;
};
class BuildTree
{
public:Node* gen;int i = 0;//遍历arrBuildTree() { gen = nullptr; }void setTree(string arr){gen = new Node;CreateBiTree(gen, arr);return;}// 核心代码void CreateBiTree(Node*& root, string strTree) //先序遍历构建二叉树{char ch;ch = strTree[i++];if (ch == '#'){root = NULL;}else{root = new Node();root->a = ch;CreateBiTree(root->leftchild, strTree);CreateBiTree(root->rightchild, strTree);}return;}
};
int main()
{int n;cin >> n;while (n--){BuildTree* bt = new BuildTree;string arr;cin >> arr;bt->setTree(arr);delete bt;}
}
1.2. 层序建立
#include <iostream>
#include <queue>
#include <string>
using namespace std;struct Node {char data;Node* leftchild;Node* rightchild;
};void pre_view(Node* root)
{if (root != nullptr){cout << root->data << ' ';pre_view(root->leftchild);pre_view(root->rightchild);}return;
}// 层序建立
void CreateBiTree(Node*& root, string strTree) {if (strTree.empty()) {root = nullptr;return;}queue<Node*> nodeQueue;int i = 0;root = new Node();root->data = strTree[i++];nodeQueue.push(root);while (!nodeQueue.empty()) {Node* current = nodeQueue.front();nodeQueue.pop();if (i < strTree.length() && strTree[i] != '#') {current->leftchild = new Node();current->leftchild->data = strTree[i];nodeQueue.push(current->leftchild);}i++;if (i < strTree.length() && strTree[i] != '#') {current->rightchild = new Node();current->rightchild->data = strTree[i];nodeQueue.push(current->rightchild);}i++;}
}int main() {string strTree = "122#3#3";Node* root = nullptr;CreateBiTree(root, strTree);// 先序遍历查看结果pre_view(root);return 0;
}
2. 递归遍历(结构体指针)
2.1. 先序遍历
void pre_send(Node* root)
{if (root != NULL){cout << (root->data);pre_send(root->leftchild);pre_send(root->rightchild);}return;
}
2.2. 中序遍历
void in_sned(Node* root)
{if (root != NULL){in_sned(root->leftchild);cout << (root->data);in_sned(root->rightchild);}return;
}
2.3. 后序遍历
void post_send(Node* root)
{if (root != NULL){post_send(root->leftchild);post_send(root->rightchild);cout << (root->data);}return;
}
3. 非递归遍历(结构体指针)
首先给出结构体:
struct Node
{int a;Node* Leftchild = nullptr;Node* Rightchild = nullptr;
}
3.1. 层次遍历
void levelorder(Node* gen)
{queue<Node*>q;q.push(gen);while (!q.empty()){Node* now = q.front();q.pop();if (now == nullptr)continue;cout << now->a;if (now->Leftchild != nullptr)q.push(now->Leftchild);if (now->Rightchild != nullptr)q.push(now->Rightchild);}
}
3.2. 后序遍历(非递归)
void postRead(Node* gen)
{stack<Node*>s;Node* root = gen, * check = nullptr;while (root != nullptr || !s.empty()){if (root != nullptr)//一直向左走{s.push(root);root = root->Leftchild;}else{root = s.top();//右节点存在且未访问if (root->Rightchild != nullptr && root->Rightchild != check){root = root->Rightchild;s.push(root);root = root->Leftchild;}else{s.pop();cout << root->a;check = root;root = nullptr;}}}
}
4. 求树的高度
int getHeight(Node* root)
{if (root == nullptr)return 0;int leftdeep = getHeight(root->Leftchild);int rightdeep = getHeight(root->Rightchild);int deep = 1 + (leftdeep > rightdeep ? leftdeep : rightdeep);return deep;
}
5. 中后序遍历构建
这个部分是我在做题的时候看到的,感觉搞懂这一块之后会对前中后序有更好的理解,这一道题就是:知道后序的规律!题目名字为:二叉树的中后序遍历构建及求叶子,可以自己搜搜看。
#include<iostream>
#include<cstring>
using namespace std;
class Tree
{
public:int* mid;int* last;int min = 10000000;Tree(int t){mid = new int[t + 5];last = new int[t + 5];for (int i = 0; i < t; i++){cin >> mid[i];}for (int i = 0; i < t; i++){cin >> last[i];}}~Tree(){delete mid, last;}int get_min(){return min;}void BuildTree(int mid_l, int mid_r, int last_l, int last_r){if (mid_l == mid_r){if (mid[mid_l] <= min)min = mid[mid_l];return;}for (int i = mid_l; i <= mid_r; i++){if (mid[i] == last[last_r]){BuildTree(mid_l, i - 1, last_l, last_l + i - mid_l - 1);BuildTree(i + 1, mid_r, last_l + i - mid_l, last_r - 1);}}}
};
int main()
{int n;cin >> n;while (n--){int t;cin >> t;Tree* tree = new Tree(t);tree->BuildTree(0, t - 1, 0, t - 1);cout << tree->get_min() << endl;delete tree;}return 0;
}6. 二叉树镜面翻转
void Mirror_inversion(Node* p)
{if (p != NULL){Mirror_inversion(p->Leftchild);Mirror_inversion(p->Rightchild);swap(p->Leftchild, p->Rightchild);}
}
7. 对称二叉树
bool judge(Node* root_1, Node* root_2)
{if (root_1 == nullptr && root_2 == nullptr){return true;}else if (root_1 == nullptr || root_2 == nullptr){return false;}else if (root_1->data != root_2->data){return false;}return judge(root_1->leftchild, root_2->rightchild) && judge(root_1->rightchild, root_2->leftchild);
}bool isSymmetric(Node* root)
{return judge(root->leftchild, root->rightchild);
}
8. 输出所有目标路径
void DFS_target(Node* node, int targetSum, vector<int>& path, vector<vector<int>>& result) {if (node == nullptr) {return;}path.push_back(node->data);if (node->leftchild == nullptr && node->rightchild == nullptr) {if (targetSum == node->data) {result.push_back(path);}}else {DFS_target(node->leftchild, targetSum - node->data, path, result);DFS_target(node->rightchild, targetSum - node->data, path, result);}path.pop_back();return;
}
9. 判断是否为子树
bool isSameTree(Node* t1, Node* t2) {// 考虑到后面子叶节点的左右节点,如果都为空就会返回Trueif (!t1 && !t2) {return true;}// 如果有一个节点有左右节点,而另一个节点没有的话就会返回false,而都有不会进入,都没有在上面会返回Trueif (!t1 || !t2) {return false;}return (t1->data == t2->data) && isSameTree(t1->leftchild, t2->leftchild) && isSameTree(t1->rightchild, t2->rightchild);
}// 判断tree1是否包含tree2的子树
bool isSubtree(Node* tree1, Node* tree2) {if (!tree1) {return false;}// tree1不空就开始考虑if (isSameTree(tree1, tree2)) {return true;}// 每一个节点向下进行考虑,如果有一个是符合的就返回Truereturn isSubtree(tree1->leftchild, tree2) || isSubtree(tree1->rightchild, tree2);
}10. 合并二叉树
void addWith(Node*& root_1, Node* root_2)
{if (root_1 == nullptr && root_2 != nullptr){root_1 = new Node;root_1->data = root_2->data;root_1->leftchild = root_2->leftchild; // Handle left childroot_1->rightchild = root_2->rightchild; // Handle right childreturn;}if (root_2 == nullptr){return;}root_1->data += root_2->data;addWith(root_1->leftchild, root_2->leftchild);addWith(root_1->rightchild, root_2->rightchild);
}
11. 带权路径和
void findDeepTree(Node* root, int* data, int dis)
{if (root == nullptr || index == n){return;}if (root->leftchild == nullptr && root->rightchild == nullptr){result = result + dis * data[index++];return;}if (root->leftchild != nullptr)findDeepTree(root->leftchild, data, dis + 1);if (root->rightchild != nullptr)findDeepTree(root->rightchild, data, dis + 1);return;
}
相关文章:

【数据结构二叉树】先序层序建立、递归非递归遍历层序遍历、树高、镜面、对称、子树、合并、目标路径、带权路径和等等
二叉树 文章目录 二叉树1. 二叉树的建立(递归创建,结构体指针形式)1.1. 先序建立1.2. 层序建立 2. 递归遍历(结构体指针)2.1. 先序遍历2.2. 中序遍历2.3. 后序遍历 3. 非递归遍历(结构体指针)3.1. 层次遍历3.2. 后序遍历(非递归) 4. 求树的高…...
Mybatis延迟加载(缓存)
延迟加载 分步查询的优点:可以实现延迟加载,但是必须在核心配置文件中设置全局配置信息:lazyLoadingEnabled:延迟加载的全局开关。当开启时,所有关联对象都会延迟加载 aggressiveLazyLoading:当开启时&…...

我对美团的看法,作为美团的股东,我都有点懵
我是美团的股东,你看股价,我都想骂人了。 这帖子就一句话。足以表明我的无奈。...
【Java】文件操作和IO
❤️ Author: 老九 ☕️ 个人博客:老九的CSDN博客 🙏 个人名言:不可控之事 乐观面对 😍 系列专栏: 文章目录 文件概念文件的分类常见的文件类型文件系统的目录结构路径 Java中的文件操作文件系统相关操作绝…...

uniapp页面间传参的方法
在uniapp中,常见的页面传参方式有以下几种: URL传参 可以在跳转页面时,在url中添加参数,通过在目标页面的onLoad函数中的options参数获取传递的参数。示例代码如下: 在源页面中: uni.navigateTo({url: …...
vsan 7.0.3部署后常见问题
一、数据库版本问题 https://partnerweb.vmware.com/service/vsan/all.json 登录可以访问 Internet 的工作站。在浏览器中打开以下链接: https://partnerweb.vmware.com/service/vsan/all.json (右键单击,另存为)将此文件另存为 all.json。如果无法保存…...

【Git】Git使用指南+上传项目踩坑总结
记录Git 使用和命令解读: git init git add .git commit -m "first commit"git branch -M maingit remote add origin https://github.com/xxx.gitgit push -u origin main 这是最经常用到的使用 git上传项目的代码,值得注意的是,…...
Django之登录注册
最近在准备上线一个网站(基于django的编程技术学习与外包服务网站),所以会将自己的在做这个项目的过程中遇到的模块业务以及所涉及到的部分技术记录在CSDN平台里,一是希望可以帮到有需要的同学,二十以供自己后续回顾学…...
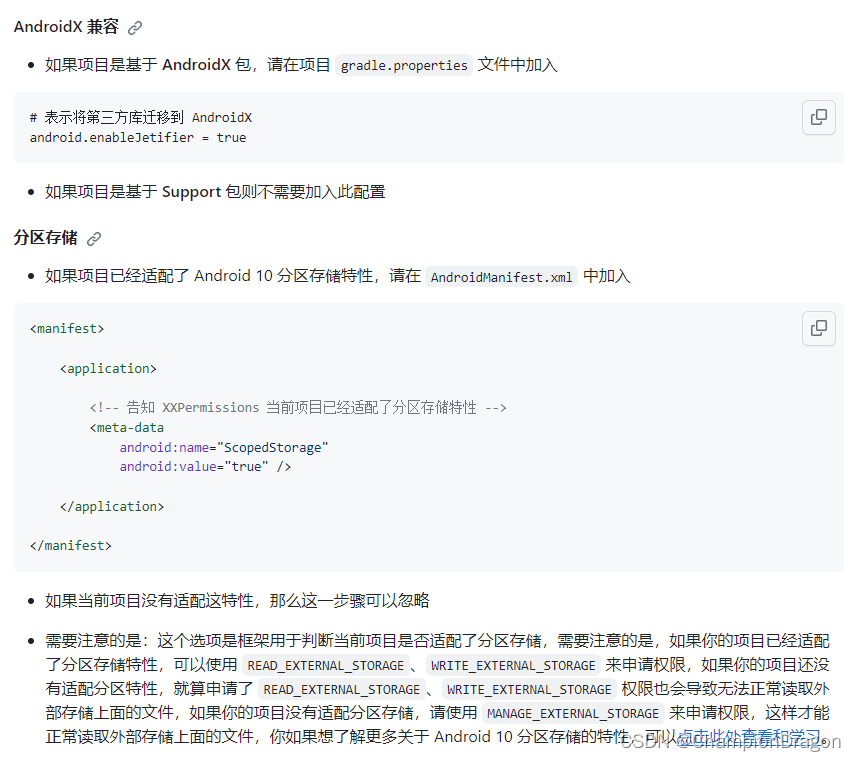
Android 10-11适配外部存储方案
Android Api 29 对文件和文件夹进行了重大更改。不允许使用外部存储,如下方法: Environment.getExternalStorageDirectory() /mnt/sdcard Environment.getExternalStoragePublicDirectory(“test”) /mnt/sdcard/test 只能使用内部存储 getExterna…...
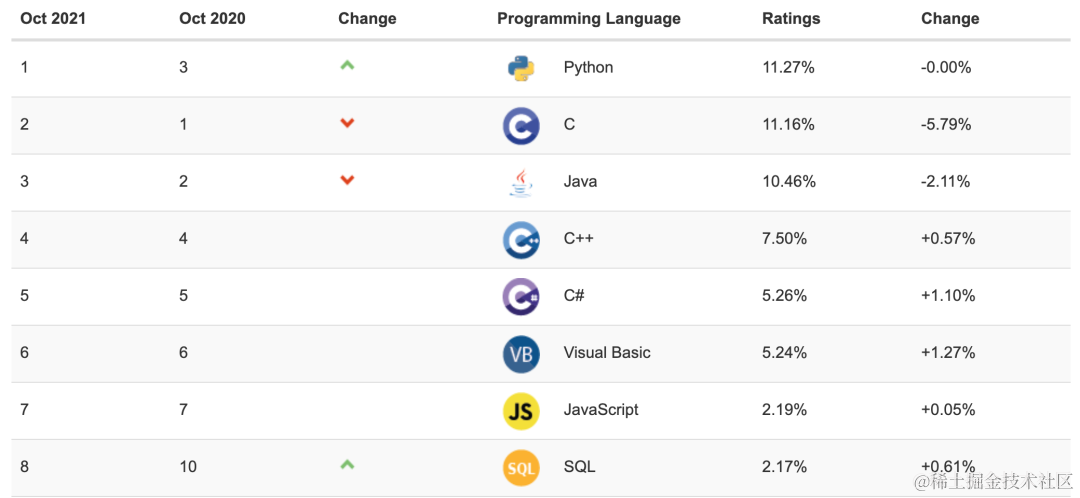
软件测试/测试开发丨Python:易学、强大、多用途的编程语言
点此获取更多相关资料 Python 发展历史 Python 是一门高级编程语言,由 Guido van Rossum(龟叔) 在 1989 年发明,设计 Python 语言的初衷是为了创造一种介于 C 和 shell 之间,简洁方便,易学易用࿰…...
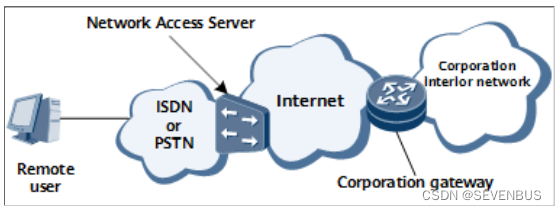
一、VPN基础
VPN基础 1、定义及特征2、VPN优势3、VPN分类4、VPN体系结构5、VPN实现的模式 —————————————————————————————————————————————————— 1、定义及特征 虚拟专用网VPN是依靠Internet服务提供商ISP和网络服务提供商NSP在公共网…...
淘宝协议最新版
我可以为您提供一些示例代码,以演示一些与电商平台相关的功能。请注意,以下代码仅为示例,具体实现还需要根据您的应用程序的架构、技术栈和需求进行调整和扩展。 1. 用户注册功能: - 后端实现:在后端,您可…...

AI“走深向实”,蚂蚁蚁盾在云栖大会发布实体产业「知识交互建模引擎」
数字化起步晚、数据分散稀疏、专业壁垒高、行业知识依赖「老师傅」,是很多传统产业智能化发展面临的难题。2023年云栖大会上,蚂蚁集团安全科技品牌蚁盾发布“知识交互建模引擎”,将实体产业知识与AI模型有机结合,助力企业最快10分…...
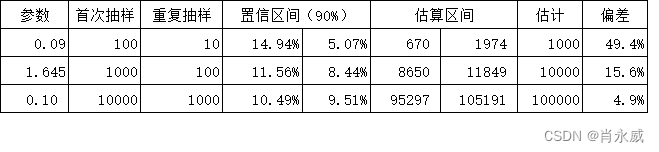
如何估计池塘里鱼的数目,周边有多少车辆?
如何估计池塘里鱼的数目? 老李想估计一下自己池塘里鱼的数量,第一天他捕捞了50条鱼做好标记,然后全放回池塘。过了几天带标记的鱼完全混合于鱼群中,他又去捕捞了168条,发现做标记的鱼有8条。帮老李估算一下池塘里的鱼…...
docker中安装rabbitMq并配置启动
目录 1. 拉取镜像并安装(此处实例安装的是最新版)2.查看docker中已安装的镜像和版本3.启动RabbitMq4.配置管理端5.安装完成 1. 拉取镜像并安装(此处实例安装的是最新版) docker pull rabbitmq2.查看docker中已安装的镜像和版本 …...

viewfs://为Hadoop 中的一个特殊文件系统
解释 viewfs:// 是 Hadoop 中的一个特殊文件系统 URI,用于访问 Hadoop 的视图文件系统(ViewFS)。 ViewFS 是 Hadoop 提供的一种虚拟文件系统,它可以将来自多个底层文件系统的文件统一管理和访问。 通过 ViewFS,你可…...
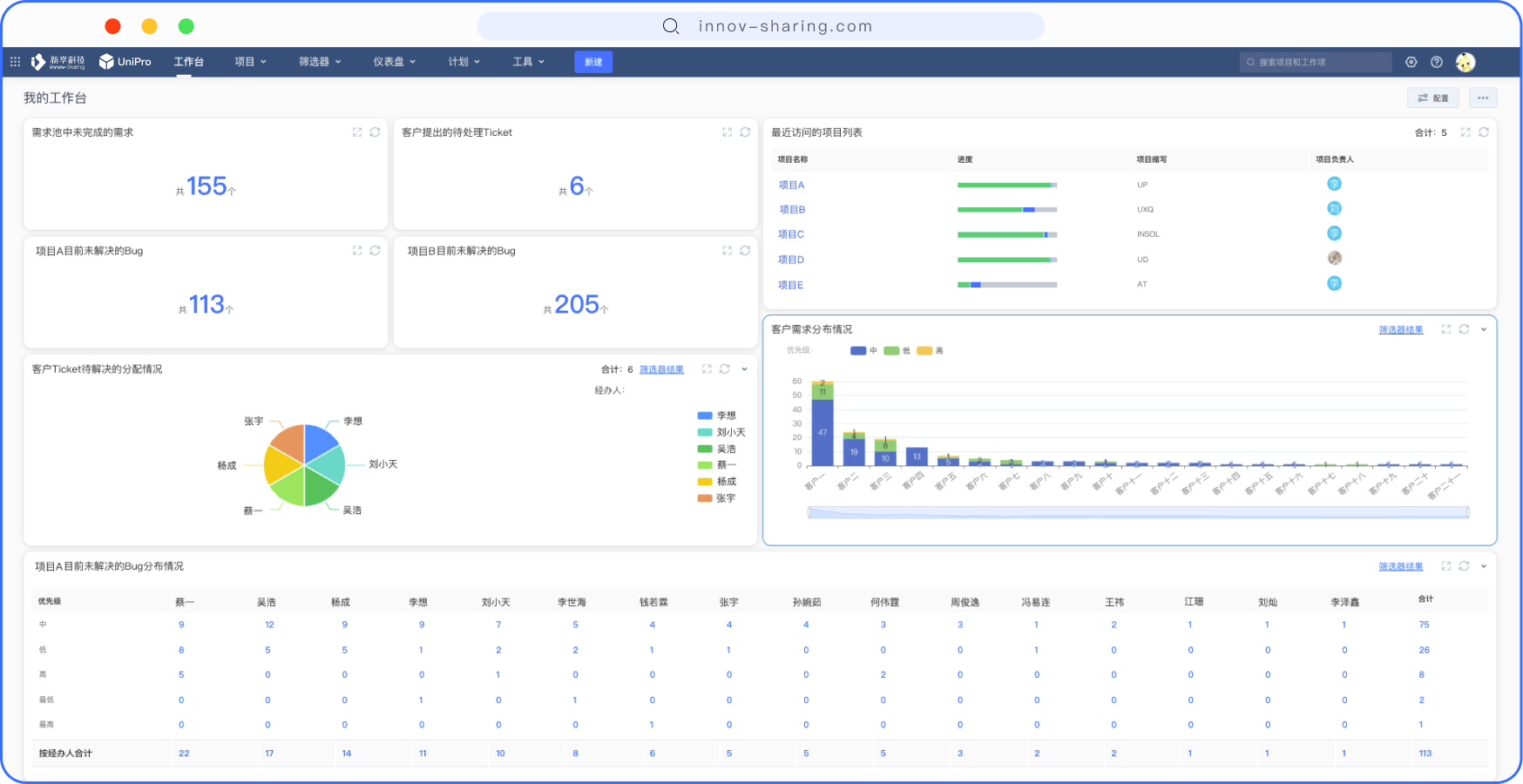
UniPro自定义个人专属工作台 大幅提升工作效率
很多研发团队在开完每日站会后,工程师的工作习惯便是打开研发管理系统,先看看自己的待办事项,或是查看同事的需求、评论,亦或是查看今日份工作的高优先级项等等。 如何方便工程师能够快速查看和了解一天的工作究竟从哪开始呢&…...
python调用飞书机器人发送文件
当前飞书webhook机器人还不支持发送文件类型的群消息,可以申请创建一个机器人应用来实现群发送文件消息。 创建机器人后,需要开通一系列权限,然后发布。由管理员审核通过后,才可使用。 包括如下的权限,可以获取群的c…...

【产品应用】一体化伺服电机在焊接设备中的应用
随着制造业的不断发展,焊接设备在许多领域都得到了广泛应用,如汽车制造、机械加工、钢结构等领域。为了提高焊接设备的性能和效率,许多厂家开始采用一体化伺服电机作为焊接设备的主要驱动部件。本文将介绍一体化伺服电机在焊接设备中的应用背…...

uni+vue3+firstUI——组件弹框使用 v-model绑定参数
说明 将框架弹框组件 封装成子组件,在页面中引用该子组件,传参并控制弹框显示与隐藏。 子组件 <template><view><wh-modal :show"showPopup" :descr"descr" maskClosable click"onClick" :buttons"…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
