探讨jdk源码中的二分查找算法返回值巧妙之处
文章目录
- 1.什么是二分查找算法
- 1.1 简介
- 1.2 实现思路
- 2.二分查找的示例
- 3.jdk 中的 Arrays.binarySearch()
- 4.jdk 中核心二分查找方法解析
- 4.1 为什么 low 是插入点
- 4.2 为什么要进行取反:-(low + 1)
- 4.3 为什么不直接返回 插入点 low 的相反数,还需要进行 +1 操作
- 4.4 可以将 +1 改为 -1 吗
- 5.未找到目标元素时根据返回值进行数组扩容
1.什么是二分查找算法
1.1 简介
二分查找算法,也称 折半查找 算法,是一种在 有序数组 中查找某一特定元素的搜索算法。
1.2 实现思路
- 初始状态下,将整个序列作为搜索区域。
- 找到搜索区域内的中间元素,和目标元素进行比对。
- 如果相等,则搜索成功;
- 如果中间元素大于目标元素,表明目标元素位于中间元素的左侧,将左侧区域作为新的搜素区域;
- 反之,若中间元素小于目标元素,表明目标元素位于中间元素的右侧,将右侧区域作为新的搜素区域;
- 重复执行第二步,直至找到目标元素。如果搜索区域无法再缩小,且区域内不包含任何元素,则表明整个序列中没有目标元素,查找失败。
2.二分查找的示例
/*** 二分查找(升序数组版)** @param array 待查找的升序数组* @param targetValue 待查找的目标值* @return 找到则返回目标值的索引,找不到返回-1*/
public static int binarySearch(int[] array, int targetValue) {// 左边界int left = 0;// 右边界int right = array.length - 1;int mid;while (left <= right) {/*考虑到 left+right 的值可能会超过 int可表示 的最大值,我们不再对他们的和直接除以2我们知道 除以2 的操作可以用 位运算 >>1 来代替但还不够,由于 (left+right) 值溢出表示负数,>>1 只是做 除以2 操作,最高位符号位不变,依旧为1表示负数,负数除以2依旧是负数这时候我们可以修改为 无符号右移 >>>1 ,低位溢出,高位补0,那么最高位符号位为0就表示正数了*/mid = (left + right) >>> 1;if (targetValue < array[mid]) {// 如果查找的目标值比中间索引值小,则缩小查找的右边界right = mid - 1;} else if (array[mid] < targetValue) {// 如果中间索引值小于查找的目标值,则缩小查找的左边界left = mid + 1;} else {// 如果找到了,就返回目标索引return mid;}}// 退出了 while 循环,说明如果没找到,则返回 -1 表示未找到return -1;
}
3.jdk 中的 Arrays.binarySearch()
public class Arrays {public static int binarySearch(int[] a, int key) {return binarySearch0(a, 0, a.length, key);}private static int binarySearch0(int[] a, int fromIndex, int toIndex,int key) {int low = fromIndex;int high = toIndex - 1;while (low <= high) {int mid = (low + high) >>> 1;int midVal = a[mid];if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found}return -(low + 1); // key not found.}
}
有了刚才二分查找的示例,其实 jdk 中二分查找方法的实现也几乎差不多,只是返回值与我们的示例不同。当目标值在数组中找不到时:
- 我们的示例会返回 -1 作为找不到元素的标识;
- 而 jdk 中是将 目标值的待插入点的变式 作为找不到元素的标识。这意味着我们可以对这个返回值做更多的事情,例如当目标值不存在时根据待插入点进行数组扩容,将目标值加入到数组中。
关于 jdk 中找不到目标值情况的返回值,我们举个例子来帮助更好理解什么是 目标值的待插入点的变式:
-
已知数组 [2, 5, 8],待查找的目标值是 4;
-
很明显,在数组中并不存在 4,那么 jdk 中的二分查找算法返回值是
-2,那么根据返回值 = -(插入点 + 1)可以推导出插入点应该是1,也就是数组索引为 1 的位置; -
即,如果需要将未找到的目标值 4 插入到数组中,应该放在索引为 1 的位置,即索引为 0 的元素
2的后面。索引 0 1 2 3 原数组 2 5 8 新数组 2 4 5 8
4.jdk 中核心二分查找方法解析
/*** 使用二分搜索算法在指定的整数数组中搜索指定的值。在进行此调用之前,必须对数组进行排序(按方法排序 sort(int[]) )。* 如果未排序,则结果未定义。如果数组包含多个具有指定值的元素,则无法保证会找到哪个元素。* 参数:* a – 要搜索的数组* key – 要搜索的值* 返回:搜索键的索引(如果它包含在数组中);否则返回 -(插入点 + 1)。* 插入点定义为将键插入数组的 点 :第一个元素的索引大于键,如果数组中的所有元素都小于指定的键,则为 a.length 。* 请注意,这保证了当且仅当找到键时返回值将为 >= 0。*/
public static int binarySearch(int[] a, int key) {return binarySearch0(a, 0, a.length, key);
}// Like public version, but without range checks.
private static int binarySearch0(int[] a, int fromIndex, int toIndex,int key) {// 左边界int low = fromIndex;// 右边界int high = toIndex - 1;while (low <= high) {int mid = (low + high) >>> 1;int midVal = a[mid];if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found}// 返回 -(插入点 + 1)return -(low + 1); // key not found.
}
我们现在需要思考两个问题:
- 为什么 low 是插入点
- 为什么要进行取反:
-(low + 1) - 为什么不直接返回 插入点 low 的相反数,还需要进行 +1 操作
- 可以将 +1 改为 -1 吗
4.1 为什么 low 是插入点
以已知了找不到目标结果为前提,有这样几件事我们需要明白:
- 随着循环次数增加,low 与 high 的距离会越来越近。直到刚进入最后一轮循环时,一定是
low == high。 - 最终未查找目标时,退出了 while 循环,会有 low > high,且
low = high + 1
// 最后一轮进入循环时,low == high
while (low <= high) {// 那么 mid == high == lowint mid = (low + high) >>> 1;int midVal = a[mid];/*要么进入 if,要么进入 else if1.当中间值小于目标值时,意味着待插入的目标值应该要在中间值索引 mid 后面一个位置,即就是 low = mid + 1,所以 low 就是插入点2.当目标值小于中间值时,意味着待插入的目标值应该要在中间值索引 mid 前面一个位置,既然要排到 mid 的前面一个位置,不就意味着要将 mid 位置挤占,将 mid 及之后的元素向后移动一位吗?所以插入点也就是当前 mid 的位置,而 low 是等于 mid 的,所以等价于 low 就是插入点 */if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found
}
4.2 为什么要进行取反:-(low + 1)
我们用正数来标识在数组中找到的目标值的索引。
因为 low + 1 一定是正数,。因此只能取反得到负数标识未找到目标值,再反推变式得到插入点。
4.3 为什么不直接返回 插入点 low 的相反数,还需要进行 +1 操作
📑 例如对于数组 [2, 5, 8],我们需要查找目标值为 -6 的索引,那么肯定是找不到的,循环结束时得到的 low 是 0,也就是目标值需要插在索引为 0 的位置。
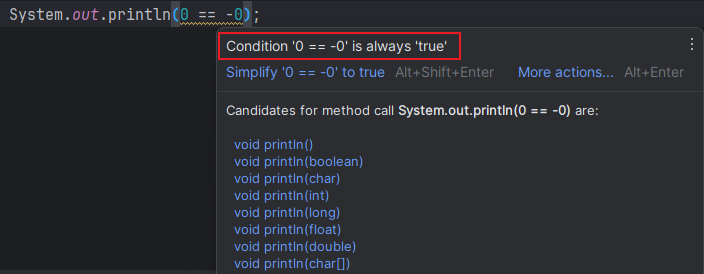
如果返回的不是 -(low + 1) 而是 -low,即 -0。在 Java 中,0 == -0 为 true,因此会被认为是索引为 0 的位置找到了目标值。
4.4 可以将 +1 改为 -1 吗
不可以,low + 1 的结果一定是正数,但 low - 1 的结果能保证一定是正数吗?是不能的,比如当 待插入点 low 为 1 时,最终返回结果 -(low - 1) 的结果为 0。那么会被认为目标值找到了且索引为 0,这是不合理的。
5.未找到目标元素时根据返回值进行数组扩容
public static void main(String[] args) {// 二分查找目标值,不存在则插入/*原始数组:[2,5,8]查找目标值:4查询不到,返回的结果为 r = -待插入点索引-1在这里带插入点索引为 1,对应 r = -2那么我们分成这几步来进行拷贝:- 1.新建数组,大小为原数组的大小+1: [0,0,0,0]- 2.将待插入点索引之前的数据放入新数组: [2,0,0,0]- 3.将目标值放入到待插入点索引的位置: [2,4,0,0]- 4.将原数组后面的数据都相继拷贝到新数组后面: [2,4,5,8]*/// 定义原数组与目标值int[] oldArray = {2, 5, 8};int target = 4;// 搜索目标值4,没有找到,返回结果为 r = -待插入点索引-1,这里的 r=-2int r = Arrays.binarySearch(oldArray, target);// r < 0 说明没有找到目标值,就插入if (r < 0) {// r = -(插入点 + 1) => 插入点 = -r - 1// 获取待插入索引int insertIndex = -r - 1;// 1.新建数组,大小为原数组的大小+1int[] newArray = new int[oldArray.length + 1];// 2.将待插入点索引之前的数据放入新数组// 新数组由 [0,0,0,0] --> [2,0,0,0]for (int i = 0; i <= insertIndex - 1; i++) {newArray[i] = oldArray[i];}// 3.将目标值放入到待插入点索引的位置// 新数组由 [2,0,0,0] --> [2,4,0,0]newArray[insertIndex] = target;// 4.将原数组后面的数据都相继拷贝到新数组后面// 新数组由 [2,4,0,0] --> [2,4,5,8]for (int i = insertIndex; i <= oldArray.length - 1; i++) {newArray[i + 1] = oldArray[i];}System.out.println(Arrays.toString(newArray)); // [2, 4, 5, 8]}}
当然,第二步和第四步拷贝的方法其实类似,我们可以自己封装一个公共方法 myArraycopy 来进行调用:
public static void main(String[] args) {// 二分查找目标值,不存在则插入/*原始数组:[2,5,8]查找目标值:4查询不到,返回的结果为 r = -待插入点索引-1在这里带插入点索引为 1,对应 r = -2那么我们分成这几步来进行拷贝:- 1.新建数组,大小为原数组的大小+1: [0,0,0,0]- 2.将待插入点索引之前的数据放入新数组: [2,0,0,0]- 3.将目标值放入到待插入点索引的位置: [2,4,0,0]- 4.将原数组后面的数据都相继拷贝到新数组后面: [2,4,5,8]*/// 定义原数组与目标值int[] oldArray = {2, 5, 8};int target = 4;// 搜索目标值4,没有找到,返回结果为 r = -待插入点索引-1,这里的 r=-2int r = Arrays.binarySearch(oldArray, target);// r < 0 说明没有找到目标值,就插入if (r < 0) {// r = -(插入点 + 1) => 插入点 = -r - 1// 获取待插入索引int insertIndex = -r - 1;// 1.新建数组,大小为原数组的大小+1int[] newArray = new int[oldArray.length + 1];// 2.将待插入点索引之前的数据放入新数组// 新数组由 [0,0,0,0] --> [2,0,0,0]myArraycopy(oldArray, 0, newArray, 0, insertIndex);// 3.将目标值放入到待插入点索引的位置// 新数组由 [2,0,0,0] --> [2,4,0,0]newArray[insertIndex] = target;// 4.将原数组后面的数据都相继拷贝到新数组后面// 新数组由 [2,4,0,0] --> [2,4,5,8]myArraycopy(oldArray, insertIndex, newArray, insertIndex + 1, oldArray.length - insertIndex);System.out.println(Arrays.toString(newArray));}}/*** 数组元素拷贝** @param oldArray 旧数组* @param oldArrayStartCopyIndex 旧数组元素开始拷贝的位置* @param newArray 新数组* @param newArrayStartCopyIndex 新数组元素开始拷贝的位置* @param copyLength 拷贝的元素长度(个数)*/
public static void myArraycopy(int[] oldArray,int oldArrayStartCopyIndex,int[] newArray,int newArrayStartCopyIndex,int copyLength) {for (int i = 0; i < copyLength; i++) {newArray[newArrayStartCopyIndex++] = oldArray[oldArrayStartCopyIndex++];}
}
但当然,其实 jdk 已经为我们提供了数组元素拷贝的方法 System.arraycopy,jdk 提供的这个方法的作用和我们自定义的 myArrayCopy 方法参数和效果是一样的,因此我们完全可以将拷贝方法修改为 System.arraycopy:
public static void main(String[] args) {// 二分查找目标值,不存在则插入/*原始数组:[2,5,8]查找目标值:4查询不到,返回的结果为 r = -待插入点索引-1在这里带插入点索引为 1,对应 r = -2那么我们分成这几步来进行拷贝:- 1.新建数组,大小为原数组的大小+1: [0,0,0,0]- 2.将待插入点索引之前的数据放入新数组: [2,0,0,0]- 3.将目标值放入到待插入点索引的位置: [2,4,0,0]- 4.将原数组后面的数据都相继拷贝到新数组后面: [2,4,5,8]*/// 定义原数组与目标值int[] oldArray = {2, 5, 8};int target = 4;// 搜索目标值4,没有找到,返回结果为 r = -待插入点索引-1,这里的 r=-2int r = Arrays.binarySearch(oldArray, target);// r < 0 说明没有找到目标值,就插入if (r < 0) {// r = -(插入点 + 1) => 插入点 = -r - 1// 获取待插入索引int insertIndex = -r - 1;// 1.新建数组,大小为原数组的大小+1int[] newArray = new int[oldArray.length + 1];// 2.将待插入点索引之前的数据放入新数组// 新数组由 [0,0,0,0] --> [2,0,0,0]System.arraycopy(oldArray, 0, newArray, 0, insertIndex);// 3.将目标值放入到待插入点索引的位置// 新数组由 [2,0,0,0] --> [2,4,0,0]newArray[insertIndex] = target;// 4.将原数组后面的数据都相继拷贝到新数组后面// 新数组由 [2,4,0,0] --> [2,4,5,8]System.arraycopy(oldArray, insertIndex, newArray, insertIndex + 1, oldArray.length - insertIndex);System.out.println(Arrays.toString(newArray));}}
相关文章:

探讨jdk源码中的二分查找算法返回值巧妙之处
文章目录 1.什么是二分查找算法1.1 简介1.2 实现思路 2.二分查找的示例3.jdk 中的 Arrays.binarySearch()4.jdk 中核心二分查找方法解析4.1 为什么 low 是插入点4.2 为什么要进行取反:-(low 1)4.3 为什么不直接返回 插入点 low 的相反数&…...

深度学习实战:基于TensorFlow与OpenCV的手语识别系统
文章目录 写在前面基于TensorFlow与OpenCV的手语识别系统安装环境一、导入工具库二、导入数据集三、数据预处理四、训练模型基于CNN基于LeNet5基于ResNet50 五、模型预测基于OpenCV 写在后面 写在前面 本期内容:基于TensorFlow与OpenCV的手语识别系统 实验环境&…...

学习整理nginx常用屏蔽规则,让网站更安全
学习整理nginx常用屏蔽规则,让网站更安全 注意一、防止文件被下载二、屏蔽非常见蜘蛛(爬虫)三、禁止某个目录执行脚本四、屏蔽某个IP或IP段 注意 在开始之前,希望您已经熟悉的Nginx常用命令(如停止,重启等…...

四十一、【进阶】索引使用SQL提示
1、SQL提示使用情景 在使用MySQL时,当一个字段参在于多个索引中时,默认情况下,MySQL会自动选择一个索引,但我们可以指定索引吗?可以忽略某一种索引吗? 答案是可以的。 前提:profession字段已经…...
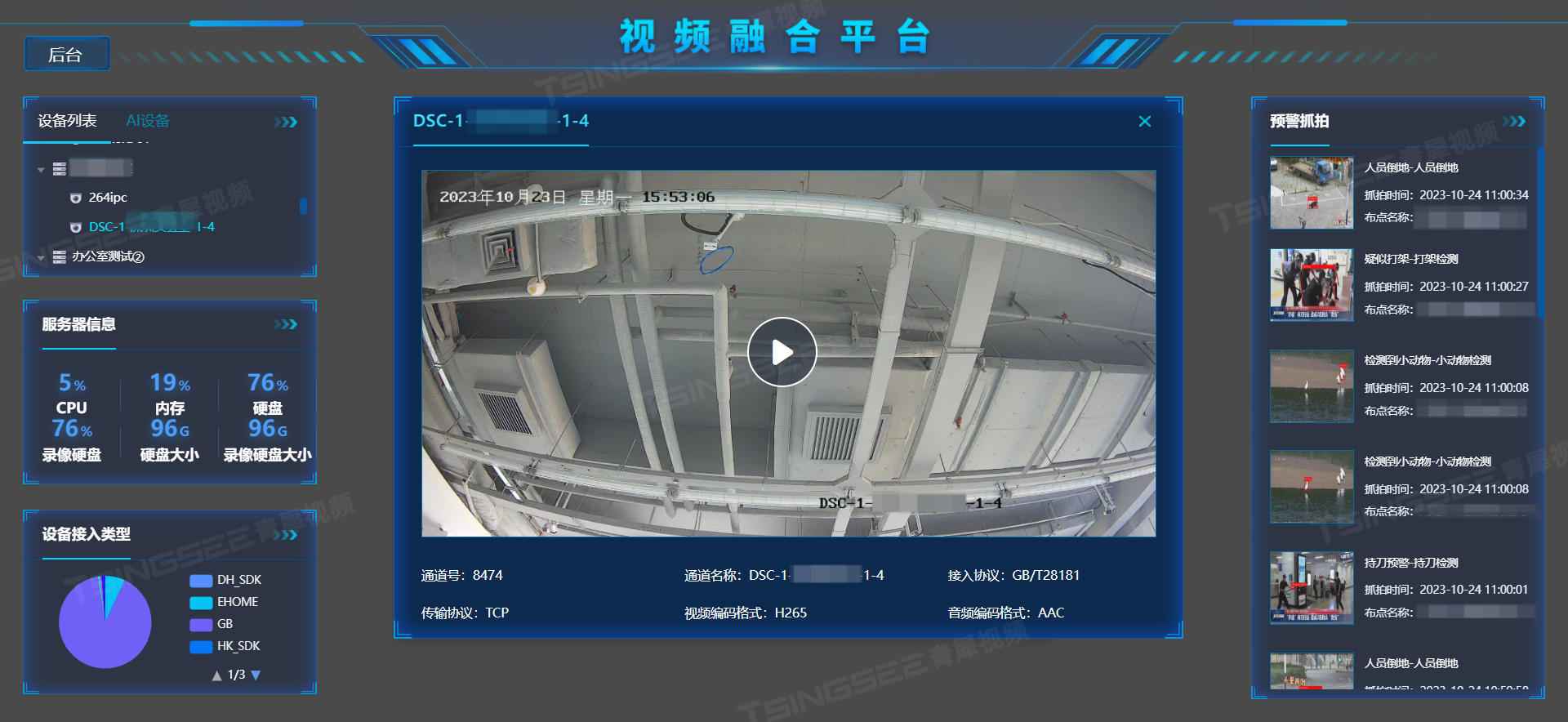
AI智能分析网关高空抛物算法如何实时检测高楼外立面剥落?
高楼外立面剥落是一种十分危险的行为,会造成严重的人身伤害和财产损失。TSINGSEE青犀智能分析网关利用高楼外立面剥落的信息,结合高空抛物算法来进行处理就可很好解决此问题。 1. 数据收集 首先,需要收集关于高楼外立面剥落的数据。这可以通…...

微信小程序 - 页面继承(非完美解决方案)
微信小程序 - 面页继承(非完美解决方案) 废话思路首页 indexindex.jsindex.jsonindex.wxml 父页面 page-basepage-base.jspage-base.wxml 子页面 page-apage-a.jspage-a.wxml 子页面 page-bpage-b.jspage-b.wxml 其它app.jsapp.jsonapp.wxss 参考资料 废…...

智能配件管理系统有什么用?企业如何实现管理数字化转型?
在当今高度信息化的时代,企业运营的各个环节都离不开准确及时的数据支持。特别是在制造业中,生产数据的记录和管理对于提高生产效率、降低成本、优化资源配置等方面具有至关重要的作用。然而,许多企业仍在采用纸质流转卡来记录生产数据&#…...

@SuppressWarnings注解使用说明
在Java编程中,我们常常会遇到一些警告(warnings),这些警告通常是对某些潜在问题的提示,虽然这些问题可能不会立即影响程序的运行,但可能会在将来引发问题。为了消除这些警告,我们可以使用Suppre…...

算法从入门到入土cpp版
1. 排序 1. 快速排序 # include<iostream> using namespace std;const int N 100010;int q[N];void quick_sort(int q[], int l, int r) {if(l>r) return;int il-1,jr1,tempq[l];while(i<j){do i;while(q[i]<temp);do j--;while(q[j]>temp);if(i<j)swa…...
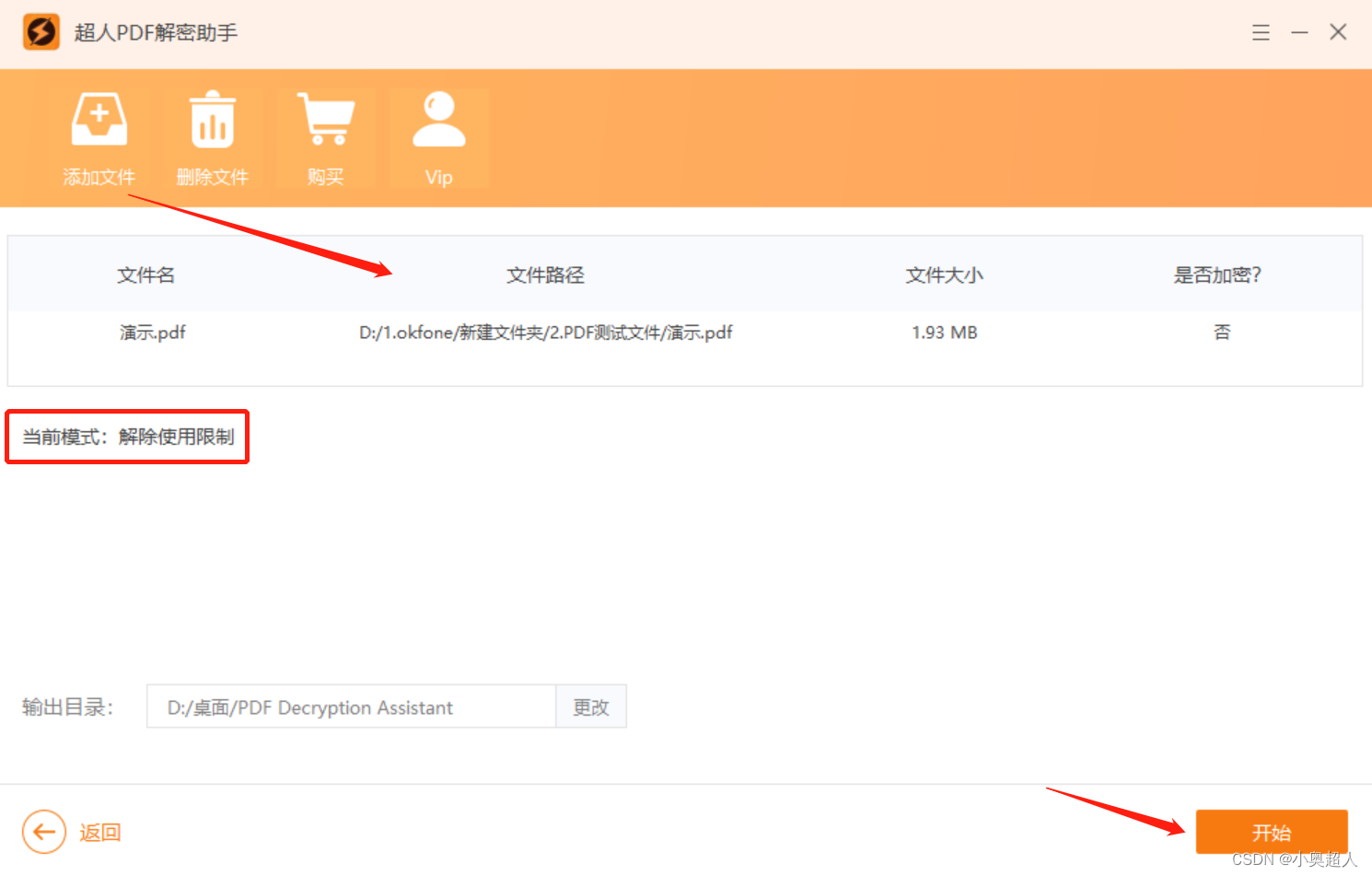
没有PDF密码,如何解密文件?
PDF文件有两种密码,一个打开密码、一个限制编辑密码,因为PDF文件设置了密码,那么打开、编辑PDF文件就会受到限制。想要解密,我们需要输入正确的密码,但是有时候我们可能会出现忘记密码的情况,或者网上下载P…...
Sqlyog 无法连接 8 版本的mysql caching_sha2_password could not be loaded
Sqlyog 无法连接 8 版本的mysql caching_sha2_password could not be loaded 1.问题背景 近期系统对Mysql 版本进行了升级,由原来的 5.7升至 8版本,在现场使用Sqlyog 作为数据库连接软件时,发现连接失败。 2.问题现象 使用Sqlyog配置完连…...
学习笔记三十三:准入控制
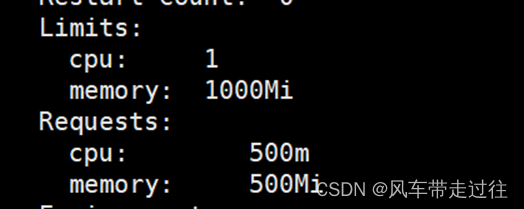
ResourceQuota准入控制器 ResourceQuota准入控制器限制cpu、内存、pod、deployment数量限制存储空间大小 LimitRanger准入控制器在limit名称空间创建pod,不指定资源,看看是否会被limitrange规则自动附加其资源限制创建pod,指定cpu请求是100m&…...

Unix/Linux C语言 获取控制台窗口尺寸
在Unix/Linux控制台编程,为了能输出好看一些,需要知道窗口宽度,当然使用支持很宽的窗口的终端也是个办法,但是实在没有很宽的终端怎么办呢,还是要从程序上想办法的。 判断控制台窗口宽度需要两个函数: isa…...
界面控件DevExpress WinForms Gauge组件 - 实现更高级别数据可视化
DevExpress WinForms控件包含了超过150个随时可用的仪表盘预设,包括圆形,数字,线性和状态指示器等,来帮助用户实现更高级的数据可视化。 DevExpress WinForms有180组件和UI库,能为Windows Forms平台创建具有影响力的业…...

vivo 自研蓝河操作系统 BlueOS 发布:支持大模型、BlueXlink 协议实现万物互联
大家好,我是 Lorin , 2023 年 11 月 1 日,在今天的 2023 年 vivo 开发者大会上,vivo 自主研发的蓝河操作系统(BlueOS)正式亮相。这款操作系统被宣传为一款面向未来的智能操作系统,具备出色的支持能力&#…...
opencv复习(很乱)
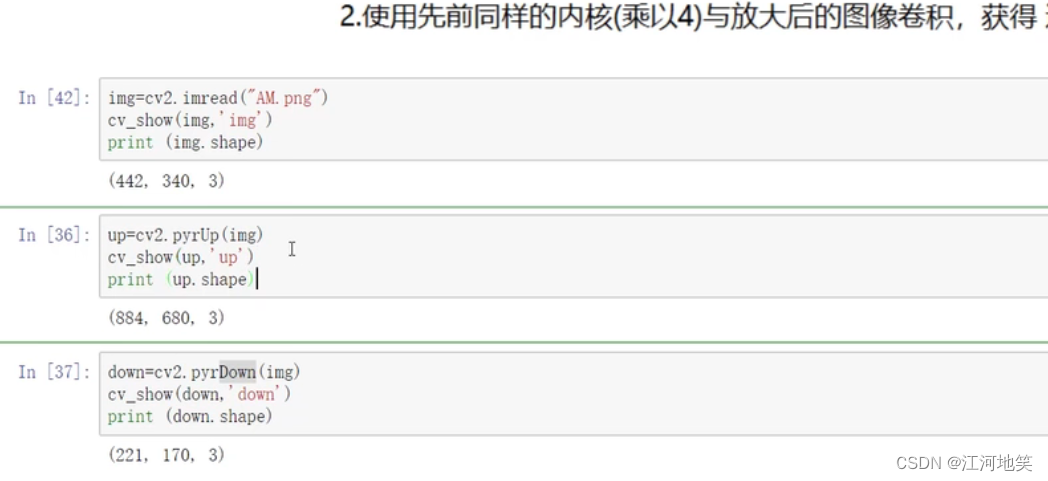
2-高斯与中值滤波_哔哩哔哩_bilibili 1、均值滤波 2、高斯滤波 3、中值滤波 4、腐蚀操作 卷积核不都是255就腐蚀掉 5、膨胀操作 6、开运算 先腐蚀再膨胀 7、闭运算 先膨胀再腐蚀 8、礼帽 原始数据-开运算结果 9、黑帽 闭运算结果-原始数据 10、Sobel算子 左-右&#x…...

于璠访谈录 | AI 框架应该和而不同?
点击以下链接收听本期 “大咖访谈” 播客,与大咖面对面: 大咖访谈链接:于璠 | AI 框架应该和而不同? 刘天栋:访谈主持,开源雨林社区顾问、开源社联合创始人、ASF member 于璠:访谈嘉宾…...
基于Springboot+MYSQL+Maven实现的宠物医院管理系统(源码+数据库+运行指导文档+项目运行指导视频)
一、项目简介 本项目是一套基于springboot框架实现的宠物医院管理系统 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 该系统功能完善、界面美观、操作简单…...

【数据结构二叉树】先序层序建立、递归非递归遍历层序遍历、树高、镜面、对称、子树、合并、目标路径、带权路径和等等
二叉树 文章目录 二叉树1. 二叉树的建立(递归创建,结构体指针形式)1.1. 先序建立1.2. 层序建立 2. 递归遍历(结构体指针)2.1. 先序遍历2.2. 中序遍历2.3. 后序遍历 3. 非递归遍历(结构体指针)3.1. 层次遍历3.2. 后序遍历(非递归) 4. 求树的高…...
Mybatis延迟加载(缓存)
延迟加载 分步查询的优点:可以实现延迟加载,但是必须在核心配置文件中设置全局配置信息:lazyLoadingEnabled:延迟加载的全局开关。当开启时,所有关联对象都会延迟加载 aggressiveLazyLoading:当开启时&…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
