Vue 3 中的 Composition API
✨理解 Vue 3 中的 Composition API
🎃 Vue 3 引入了全新的 Composition API，相较于传统的 Options API，它具备许多优势和适用场景。下面将介绍 Composition API 的优势和使用场景，并为你带来更好的开发体验。
🎁 Composition API 的优点
- 🌟 更灵活的组合性逻辑：Composition API 允许将相关逻辑组合在一起，而不再由生命周期钩子或选项来分散编写。这使得代码更直观，能够更好地组织和管理功能相关代码，提高代码的可读性、可维护性和重用性。
- 🌟 更好的可读性和维护性：通过将相关逻辑集中在一起，代码在逻辑上更加紧凑和清晰。不同功能的代码能够被隔离、封装和测试，降低了代码的耦合性，使代码更易于阅读、理解和维护。
- 🌟 更好的类型推断和编辑器支持：Composition API 支持更好的类型推断，在使用 TypeScript 时，编译器能够更准确地推断和验证代码中的类型。这使得在编码过程中，类型错误更容易被捕获，提供了更好的代码补全、错误提示和重构支持。
- 🌟 更好的响应式系统：Composition API 引入了
ref、reactive和watch等 API，使响应式系统更加直观和灵活。开发者能够更精确地控制数据的依赖跟踪和更新，提高了数据更新的性能和效率。 - 🌟 更好的逻辑复用和可测试性：通过自定义 Hooks 的方式，可以将通用的逻辑封装成可重用的代码块。这样可以更好地实现逻辑的复用和抽象，减少重复编写相似的代码，提高代码的可测试性和可维护性。
💔 Composition API 的缺点
- 💢 学习曲线：对于熟悉 Options API 的开发者来说，切换到 Composition API 需要一定的学习成本。Composition API 的学习曲线可能会有些陡峭，需要一段时间去适应和理解其使用方式和设计理念。
- 💢 与生态系统的兼容性：由于 Composition API 是 Vue 3 新引入的特性，一些第三方库和插件可能还没有完全适配。在使用 Composition API 时需要关注与现有生态系统的兼容性，并可能需要进行额外的适配和调整。
- 💢 小规模项目不一定有优势：对于简单的、规模较小的项目来说，使用 Composition API 可能会显得繁琐和过度设计，Options API 在这种情况下可能更直接和简单。
🚀总结
需要注意的是，尽管 Composition API 带来了许多优点，但并不意味着传统的 Options API 已经过时或不再适用。在选择 API 风格时，应根据具体项目的需求和特点进行选择，也可以在不同的 API 风格之间灵活切换使用。
相关文章：
Vue 3 中的 Composition API
✨理解 Vue 3 中的 Composition API 🎃 Vue 3 引入了全新的 Composition API，相较于传统的 Options API，它具备许多优势和适用场景。下面将介绍 Composition API 的优势和使用场景，并为你带来更好的开发体验。 🎁 Co…...
《TCP/IP详解 卷一：协议》第5章的IPv4数据报的总长度字段出现“不需要大于576字节的IPv4数据报“相关内容的解释
《TCP/IP详解 卷一：协议》第5章的IPv4数据报的总长度字段的一些解释，出现以下内容（有省略）： ....另外，主机不需要接收大于576字节的IPv4数据报.....以避免576字节的IPv4限制。 英文原文的内容（有…...
PO-java客户端连接错误can not connect to server
问题描述： 换电脑或者网络环境改变了，PO下载EST ID的jnlp提示can not connect to server*** ；**message server***这类错误 原因分析： 基本上都是PO消息服务器连接不上导致的错误，原理有均衡负载对应的IP转接后端口不…...
PM2 vs Kubernetes：在部署 Node.js 服务时使用哪个？
Node.js 已成为 Web 开发中的热门技术之一，但如果我们想成功地将 Node.js 应用程序交付给用户，我们需要考虑部署和管理这些应用程序。两个常见的选项是 PM2 和 Kubernetes。PM2 是一个用于运行和管理 Node.js 应用程序的进程管理器，它能够创建…...
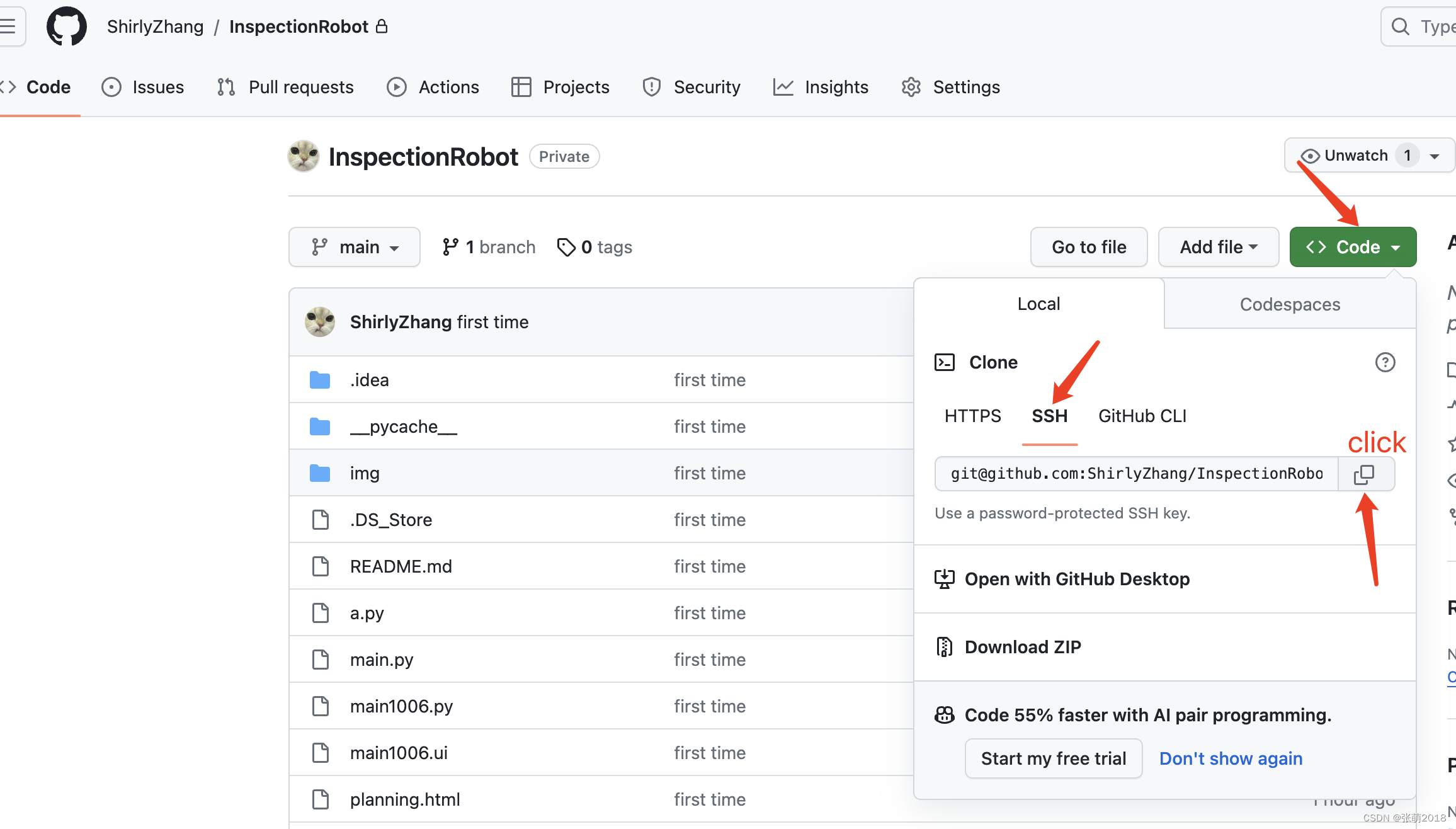
配置git并把本地项目连接github
一.配置git 1.下载git（Git），但推荐使用国内镜像下载（CNPM Binaries Mirror） 选好64和版本号下载，全部点下一步 下载完成后打开终端，输入 git --version 出现版本号则说明安装成功 然后继续…...
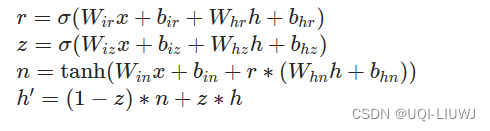
pytorch笔记 GRUCELL
1 介绍 GRU的一个单元 2 基本使用方法 torch.nn.GRUCell(input_size, hidden_size, biasTrue, deviceNone, dtypeNone) 输入：（batch，input_size） 输出和隐藏层：（batch，hidden_size…...
不解压，也能列出文件信息
gz文件，不解压，查看压缩前文件的大小： gzip -l ~$ ll -rw-r--r-- 1 fee fee 17343450 Nov 2 12:02 xxx.log.2023-11-02T04-02-56.000.1 -rw-r--r-- 1 fee fee 3150599 Nov 2 12:02 xxx.log.2023-11-02T04-02-56.000.1.gz ~$ gzip -l gb…...
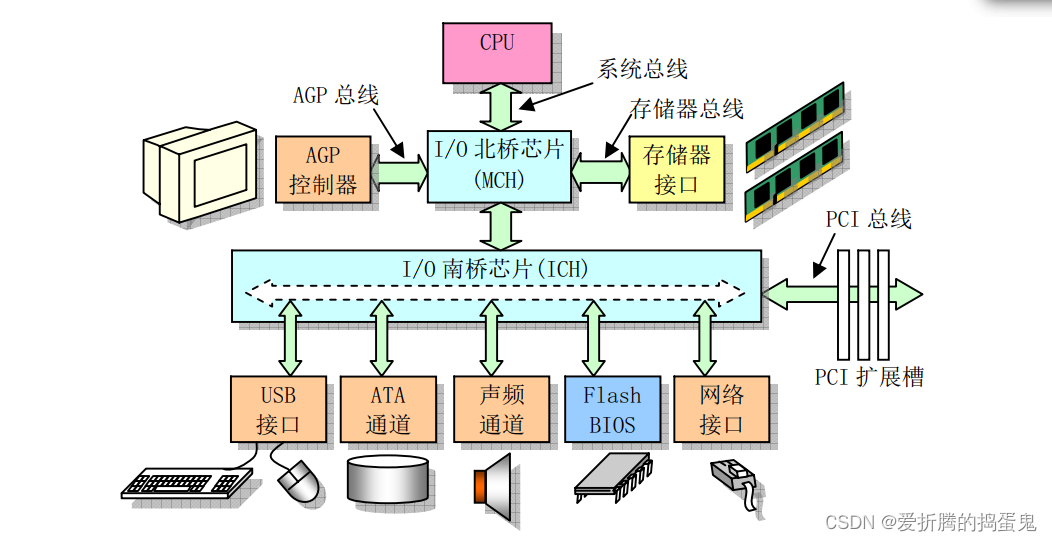
微型计算机组成原理
1、微型计算机组成 一个传统微型计算机硬件组成如下图 CPU通过地址线、数据线和控制信号线组成的本地总线（内部总线）与系统其他部分进行数据通信。 地址线用于提供内存或I/O设备的地址，即指明需要读/写数据的具体位置；数据线用…...
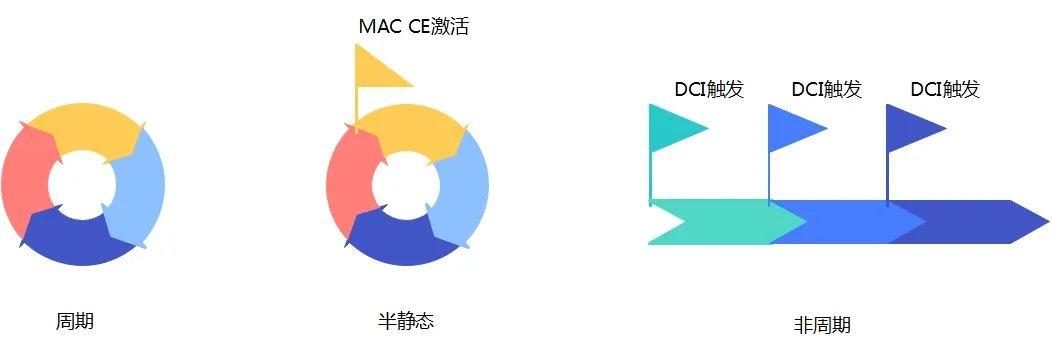
基站/手机是怎么知道信道情况的？
在无线通信系统中，信道的情况对信号的发送起到至关重要的作用，基站和手机根据信道的情况选择合适的资源配置和发送方式进行通信，那么基站或者手机是怎么知道信道的情况呢？ 我们先来看生活中的一个例子，从A地发货到B地…...
进程/线程
进程是资源单位, 线程是执行单位。 每一个进程至少要有一个线程，启动每一个程序默认都会有一个主线程 1.多线程的两种实现 from threading import Thread#方法一 def func(name):for i in range(10):print(name, i)if __name__ __main__:t Thread(targetfunc, …...
Python 应用 之 转换音频格式
目录 一、python音频转换 1、pydub 音频包安装 2、 ffmpeg安装 1）、解压后，添加到环境变量中 2）、可以直接放在python安装目录下 3、python程序 1）、引入相关包 2）、重命名 3）、to Mp3 4…...
Oracle JDK 和OpenJDK两者有什么异同点
Oracle JDK 和 OpenJDK 是两种不同版本的 Java Development Kit（Java 开发工具包），它们都提供了用于开发 Java 程序的一系列工具和库。以下是它们之间的一些主要异同点： 相同点： 功能：在大多数情况下&…...
GPT引发智能AI时代潮流
最近GPT概念爆火，许多行业开始竞相发展AI ，工作就业也将面临跳转，目前测试就业形势就分为了两大类，一类是测试行业如功能、性能、自动化综合性人才就业技能需求，另一类便是AI测试行业的需求普遍增长，原本由…...
FreeSWITCH mrcp-v2小记
最近得知有人受mrcp的困扰，于是写了这篇小文，希望能有所帮助 FreeSWITCH版本选择 目前当然选择1.10.10，不建议老版本，差别在于老版本用到的libmrcp比较旧，是1.2版本，bug比较多，有时会crash&am…...
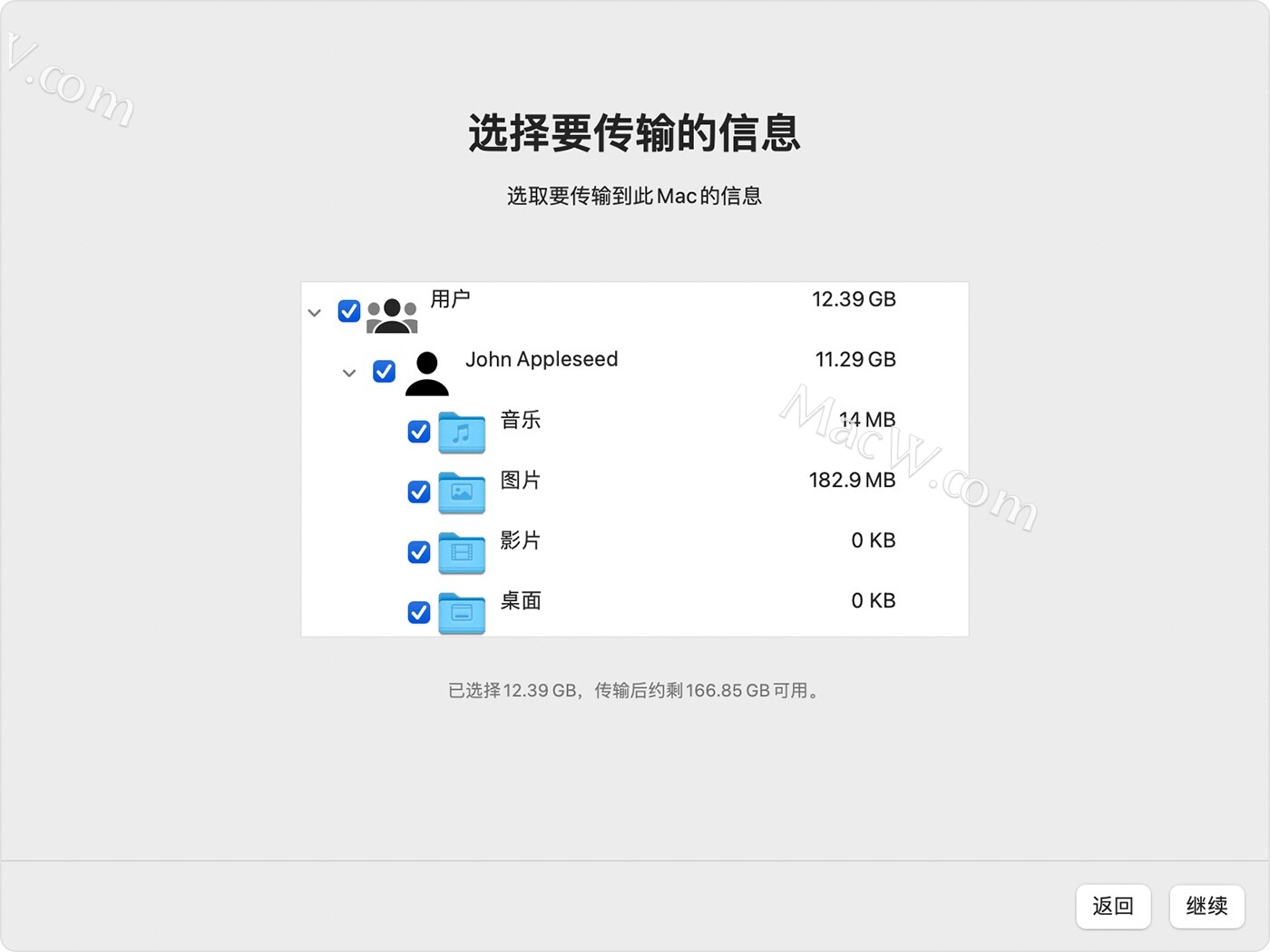
如何将你的PC电脑数据迁移到Mac电脑？使用“迁移助理”从 PC 传输到 Mac的具体操作教程
有的小伙伴因为某一项工作或者其它原因由Windows电脑换成了Mac电脑，但是数据和文件都在原先的Windows电脑上，不知道怎么传输。接下来小编就为大家介绍使用“迁移助理”将你的通讯录、日历、电子邮件帐户等内容从 Windows PC 传输到 Mac 上的相应位置。 在…...
Elasticsearch集群搭建、数据分片以及位置坐标实现附近的人搜索
集群搭建、数据分片 es使用两种不同的方式来发现对方： 广播单播也可以同时使用两者，但默认的广播，单播需要已知节点列表来完成 一 广播方式 当es实例启动的时候，它发送了广播的ping请求到地址224.2.2.4:54328。而其他的es实例使用同样的集群名称响应了这个请求。 一般这…...
深度学习_3 数据操作之线代，微分
线代基础 标量 只有一个元素的张量。可以通过 x torch.tensor(3.0) 方式创建。 向量 由多个标量组成的列表（一维张量）。比如 x torch.arange(4) 就是创建了一个1*4的向量。可以通过下标获取特定元素（x[3]），可以通…...
树莓派安装Ubuntu22.04LTS桌面版
工具：树莓派4B Raspberry Pi 自己下载的ubuntu22.04LTS img磁盘镜像文件 这里有一个小技巧：这个Raspberry Pi的选择镜像的时候在最后面一行可以选择自定义的镜像，哈哈哈哈，这就使得我们可以自己下载，而且知道那个文…...
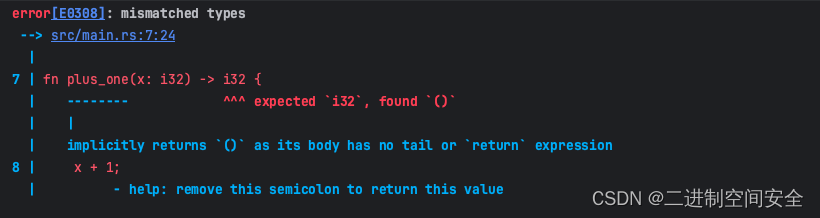
Rust编程基础之函数和表达式
1.Rust函数 在之前的文章中,我们已经见到了一个函数:main函数, 它是很多程序的入口点。也见过 fn 关键字，它用来声明新函数。 Rust 代码中的函数和变量名使用 snake case 规范风格。在 snake case 中，所有字母都是小写并使用下划线分隔单词。这是一个包…...
关于preempt count的疑问
Linux中的preempt_count - 知乎 https://www.cnblogs.com/hellokitty2/p/15652312.html LWN：关于preempt_count()的四个小讨论！-CSDN博客 主要是参考这些文章 之前一直认为只要是in_interrupt()返回非0值，那么就可以认为当前在中断上下文。即…...
利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向： 逆向设计 通过神经网络快速预测微纳结构的光学响应，替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性，不同版本的Docker对内核版本有不同要求。例如，Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本，Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机：Ubuntu 20.04.6 LTSHost：ARM32位交叉编译器：arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成：MAC头部frame bodyFCS，其中MAC是固定格式的，frame body是可变长度。 MAC头部有frame control，duration，address1，address2，addre…...
el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
如何在最短时间内提升打ctf（web)的水平？
刚刚刷完2遍 bugku 的 web 题，前来答题。 每个人对刷题理解是不同，有的人是看了writeup就等于刷了，有的人是收藏了writeup就等于刷了，有的人是跟着writeup做了一遍就等于刷了，还有的人是独立思考做了一遍就等于刷了。…...
docker 部署发现spring.profiles.active 问题
报错： org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
Netty从入门到进阶（二）
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架，用于…...
解决：Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象： android studio报错： [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决： 不要动CMakeLists.…...