Codeforces 1855E 数学期望 + DP
题意
传送门 Codeforces 1855E Expected Destruction
题解
将 S i S_i Si 运动至 S i + 1 S_{i+1} Si+1 的情况看作后者消失,则 S i S_i Si 在碰到 S i + 1 S_{i + 1} Si+1 前, S i + 1 S_{i + 1} Si+1 必然存在。
根据数学期望的线性性质,可以独立地考虑每一个 S i S_i Si 在碰到 S i + 1 S_{i+1} Si+1 时的期望步数。对于每一对 S i , S i + 1 S_i,S_{i+1} Si,Si+1,考虑每一步, S i S_i Si 与 S i + 1 S_{i+1} Si+1 前进的概率都为 1 / 2 1/2 1/2,则 D P DP DP 求解即可。令 d p [ x ] [ y ] dp[x][y] dp[x][y] 为 S i S_i Si 与 S i + 1 S_{i+1} Si+1 距离为 x x x 且 S i + 1 S_{i+1} Si+1 与 m + 1 m + 1 m+1 距离为 y y y 为初始状态情况下 S i S_i Si 对答案的贡献,则答案为 ∑ d p [ S i + 1 − S i ] [ ( m + 1 ) − S i + 1 ] \sum dp[S_{i+1}-S_i][(m + 1) - S_{i + 1}] ∑dp[Si+1−Si][(m+1)−Si+1]。总时间复杂度 O ( m 2 ) O(m^2) O(m2)。
#include <bits/stdc++.h>
using namespace std;
constexpr int MOD = 1e9 + 7;
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;vector<int> a(n);for (int i = 0; i < n; ++i) {cin >> a[i];}a.push_back(m + 1);using ll = long long;auto power = [&](int x, int n) {int res = 1;while (n > 0) {if (n & 1) {res = (ll)res * x % MOD;}x = (ll)x * x % MOD, n >>= 1;}return res;};int inv2 = power(2, MOD - 2);vector<vector<int>> dp(m + 1, vector<int>(m + 1));for (int w = 1; w <= m; ++w) {for (int left = w; left > 0; --left) {int right = w - left;if (right > 0) {dp[left][right] = (ll)(1 + dp[left - 1][right] + dp[left + 1][right - 1]) % MOD * inv2 % MOD;} else {dp[left][right] = 1 + dp[left - 1][right];}}}int res = 0;for (int i = 0; i < n; ++i) {(res += dp[a[i + 1] - a[i]][m + 1 - a[i + 1]]) %= MOD;}cout << res << '\n';return 0;
}相关文章:

Codeforces 1855E 数学期望 + DP
题意 传送门 Codeforces 1855E Expected Destruction 题解 将 S i S_i Si 运动至 S i 1 S_{i1} Si1 的情况看作后者消失,则 S i S_i Si 在碰到 S i 1 S_{i 1} Si1 前, S i 1 S_{i 1} Si1 必然存在。 根据数学期望的线性性质&…...

5-1CComplex运算符重载为友元
以下是一个用运算符重载为友元重载的方法重做复数加减法的运算,请填空完成程序。 #include <iostream> using namespace std; class CComplex { private:double real; double imag; public:CComplex(double r0.0,double i0.0){ real(r), imag(i)}friend…...

Vue3.0 watch和watchEffect监听器:VCA
简介 在项目中,有时候检测一个变量的值是否反升了变化。通常使用的watch或者使用低效的循环判断。 在次vue中给我们设置了深度监测数据繁盛变化的方法。 1.vue中提供了在watch监听时设置deep:true 就可以实现对对象的深度监听; 2.immediate:true,代表watch里面声明了…...

1360. 日期之间隔几天
1360. 日期之间隔几天 Java代码: 【DateFormat】DateFormat用于实现日期的格式化 import java.text.DateFormat; import java.text.ParseException; import java.text.SimpleDateFormat; import java.util.Date; // 好像已过时class Solution {public int daysBet…...
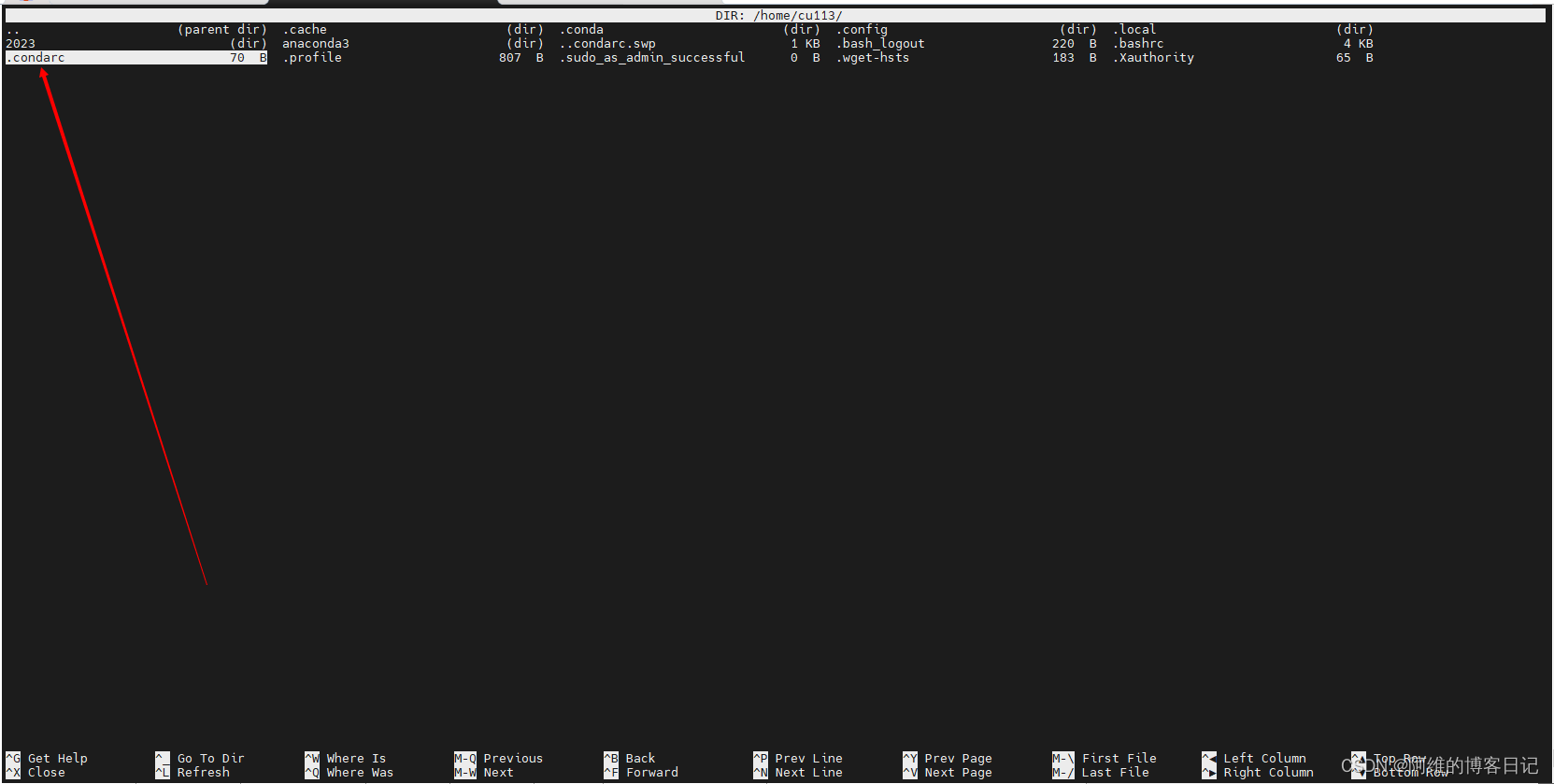
ubuntu配置 Conda 更改默认环境路径
我的需求是以后凡是新建一个虚拟环境都需要安装在一个挂载了大容量的分区/data里面 /home里面的是即将爆满但是还能塞点东西的硬盘. 如果您想要永久更改 Conda 的默认环境路径,可以编辑 Conda 的配置文件。首先,找到 Conda 的配置文件通常是 .condarc 文…...
华山编程培训中心——工业相机飞拍
飞拍功能是一种高速运动图像采集技术,通过降低相机的曝光时间来拍摄快速移动的对象,以提高工作效率和加快生产速度。下面视频演示工业相机飞拍: 上位机控制工业相机飞拍演示 一. 飞拍对相机硬件的要求 全局快门相机:飞拍要求相机…...

linux 释放缓存命令并做成定时任务
这个命令组合可以实现将待写入的数据同步到磁盘中,然后释放页面缓存。具体命令为: sync; echo 1 > /proc/sys/vm/drop_caches 第一个命令 sync 是将所有待写入磁盘的数据刷新到磁盘中,确保数据写入完成。第二个命令 echo 1 > /proc/…...
求解一个整数中含多少个1
1.问题描述:给定一个整数,统计其对应的二进制中含有1的个数。比如8(0000 1000),对应的二进制数中,只含有一个1. 2.设计思路:对x取余:zx%2。如果z!0,说明x的末尾不是为1.对于一个二进制x4x3x2x1…...

js编写一个函数判断所有数据类型
一、typeof 在 JavaScript 里使用 typeof 来判断数据类型,只能区分基本类型,即 “number”,”string”,”undefined”,”boolean”,”object” 五种。 对于数组、对象来说,其关系错综复杂&…...
)
Python对于时间相关模块的学习记录(time,datetime等模块)
1,time.time() 获得从计算机开始出生到现在的秒数(也成时间戳),可以时间相减计算流逝时间 说明 :擅长时间相减计算流逝时间 导入方法 import time import time# 1,time.time 获得从计算机开始出生到…...

【C#】获得所有可见窗口信息
【背景】 由于自己的瘦客户端上的Windows自带截图软件功能被阉割,所以自己写了一个,其中有窗口截图功能,涉及到获得所有可见窗口的信息。 【代码】 public WindowInfo[] GetAllDesktopWindows(){//用来保存窗口对象 列表List<WindowInf…...

ffmpeg的基本功能介绍
之前对ffmpeg有一个模糊的印象,后来经过一些项目对ffmpeg有了深入的认识,这里总结下。 最开始对ffmpeg的印象是可以对视频进行一些处理操作,但是做哪些操作又不是很清楚,知其然不知其所以然。下面对于ffmpeg的功能进行一个总结&a…...

QECon大会亮相产品,支持UI自动化测试?RunnerGo
最近在gitee上看见一款获得GVP(最有价值开源项目)的测试平台RunnerGo,看他们官网介绍包含了接口测试、性能测试、自动化测试。知道他们有saas版可以试用,果断使用了一下,对其中场景管理和性能测试印象深刻,…...

Linux开关机相关的命令解析
前言 Linux直接拔电源关机 ,内存中的东西还没保存到硬盘。所以有时候会导致数据丢失或者有些服务起不来。所以最好直接命令行关机就像windows电脑需要界面关机一样。而不是强制拔电源 关机命令 halt halt:关机但是不关闭电源,需要手动关闭电源(加p参数会关闭电源),不…...

C++二分查找算法的应用:俄罗斯套娃信封问题
本文涉及的基础知识点 二分查找 题目 给你一个二维整数数组 envelopes ,其中 envelopes[i] [wi, hi] ,表示第 i 个信封的宽度和高度。 当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗…...

redis如何保证和mysql数据的一致性
Redis和MySQL是两种不同的数据库系统,它们在数据一致性方面有不同的特点和应用场景。保证Redis和MySQL数据的一致性通常需要考虑以下几个方面: 双写策略: 一种常见的方法是采用双写策略,即将更新操作同时写入Redis和MySQL。这确保…...

SpringBoot整合Redisson,赶紧整起来!
SpringBoot整合Redisson 一、Redisson 是什么?二、使用场景三、使用步骤1.引入相关依赖2.application.yml配置3.创建RedissonConfig4.开始使用 总结 提示:以下是本篇文章正文内容 一、Redisson 是什么? Redisson是一个基于Java的开源的、高…...

测试Whisper效果
先去官方上面看看,是否有对应的测试结果 简单找了一下,没找到对应的测试数据 去hugging face 上面找对应的数据集,发现没有现成的数据 找到了几个数据集,但是是收费的 101 Hours – Scene Noise Data by Voice Recorder 1,29…...
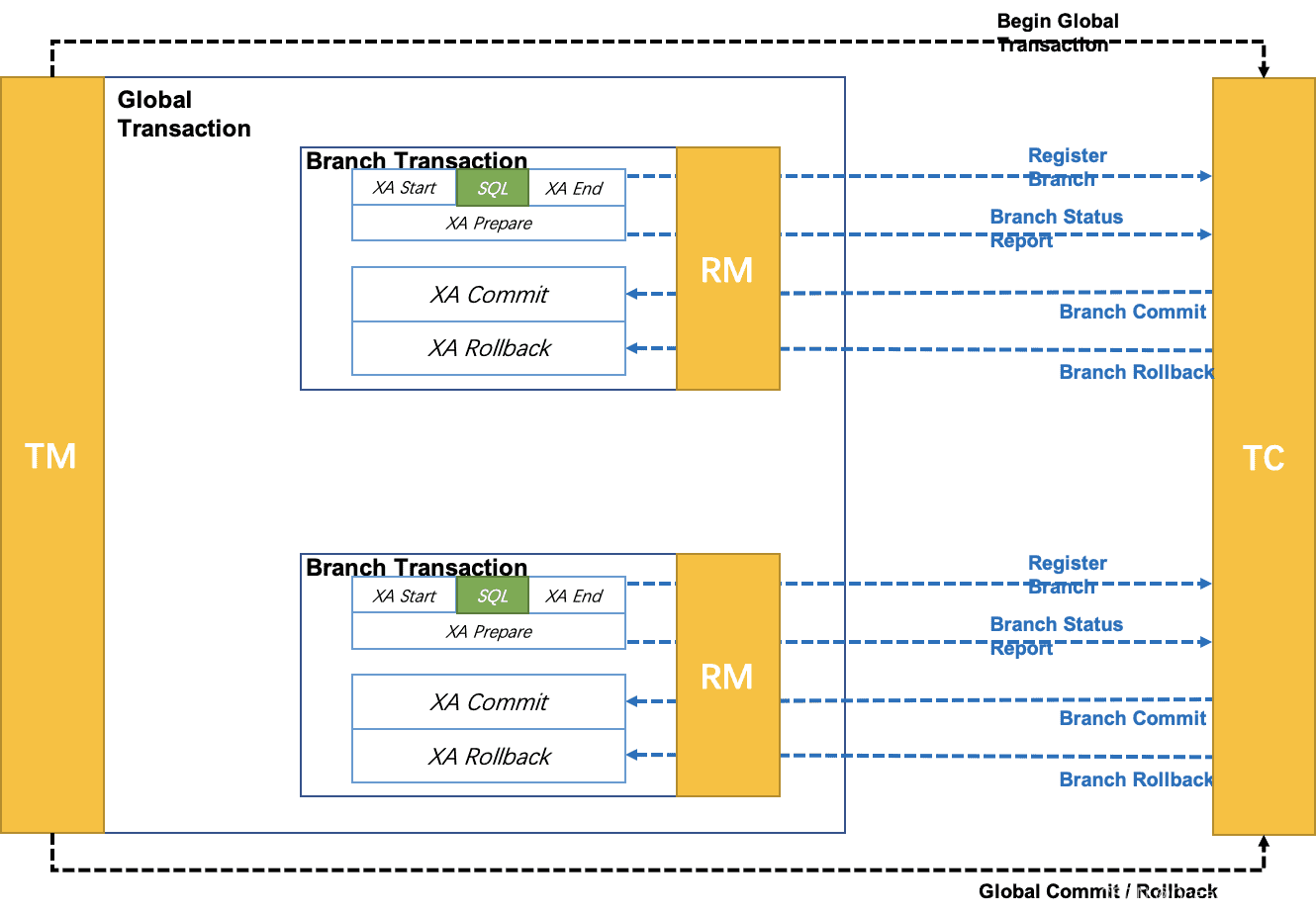
Seata 四种事务模式
Seata 是一款开源的分布式事务解决方案,致力于提供高性能和简单易用的分布式事务服务。Seata 将为用户提供了 AT、TCC、SAGA 和 XA 事务模式,为用户打造一站式的分布式解决方案。 全文参考文献:中文文档 TC (Transaction Coordinator) - 事务…...
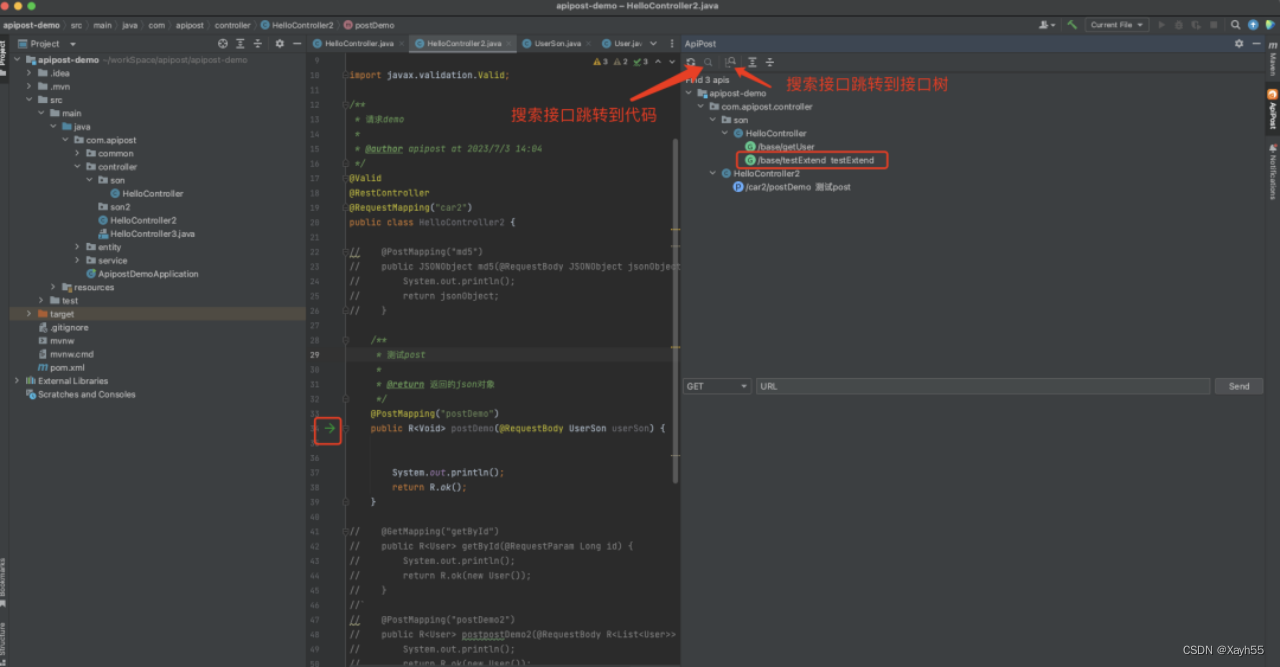
超好用的IDEA插件推荐,写完代码直接调试接口
Apipost推出IDEA插件非常省时高效,写完代码直接可以进行调试,而且支持生成接口文档,真是后端神器啊! 可以点击下方链接安装更新或在插件商店中搜索安装 下载链接:https://plugins.jetbrains.com/plugin/22676-apipos…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用
Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用 Linux 内核内存管理是构成整个内核性能和系统稳定性的基础,但这一子系统结构复杂,常常有设置失败、性能展示不良、OOM 杀进程等问题。要分析这些问题,需要一套工具化、…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...
