刷题笔记day08-字符串01
344. 反转字符串
思路1:使用双指针的方法,前后交换
func reverseString(s []byte) {// 思路1:使用双指针进行交换// 思路2:使用库函数进行交换for i, j := 0, len(s) - 1; i < j; {s[i], s[j] = s[j], s[i]i++j--}
}
思路2:使用库文件,进行翻转。目的是为了熟悉库,方便后面工作用。
class Solution:def reverseString(self, s: List[str]) -> None:"""Do not return anything, modify s in-place instead."""s.reverse()
541. 反转字符串 II
设置好边界条件,然后调用上一题写的双指针交换的函数既可搞定。
func reverseStr(s string, k int) string {// 双指针法s2 := []byte(s)start := 0length := len(s)for start < length {if (start + k >= length) {reverse(s2, start, length - 1)} else {reverse(s2, start, start + k - 1)}start += 2*k}return string(s2)
}func reverse(s []byte, start, end int) {for i, j := start, end; i < j; {s[i], s[j] = s[j], s[i]i++j--}
}LCR 122. 路径加密
func replaceSpace(s string) string {// 使用双指针的方法by := []byte(s)spaceCount := 0for i := 0; i < len(s); i++ {if s[i] == ' ' {spaceCount++}}// 为什么是*2,而不是*3,因为原先的空格也占一个空格。tmp := make([]byte, spaceCount*2)by = append(by, tmp...) // 用...展开切片// b是原切片的指针,e是扩容后的指针。从后往前扫,不断的赋值for b, e := len(s)-1, len(by)-1; e > b; {if (by[b] == ' ') {by[e] = '0'by[e-1] = '2'by[e-2] = '%'e -= 2} else {by[e] = by[b]}b--e--}return string(by)
}相关文章:

刷题笔记day08-字符串01
344. 反转字符串 思路1:使用双指针的方法,前后交换 func reverseString(s []byte) {// 思路1:使用双指针进行交换// 思路2:使用库函数进行交换for i, j : 0, len(s) - 1; i < j; {s[i], s[j] s[j], s[i]ij--} }思路2&…...

Pure-Pursuit 跟踪双移线 Gazebo 仿真
Pure-Pursuit 跟踪双移线 Gazebo 仿真 主要参考学习下面的博客和开源项目 自动驾驶规划控制(A*、pure pursuit、LQR算法,使用c在ubuntu和ros环境下实现) https://github.com/NeXTzhao/planning Pure-Pursuit 的理论基础见今年六月…...

Selenium学习(Java + Edge)
Selenium /səˈliːniəm/ 1. 简介 Selenium是一个用于Web应用程序自动化测试工具。Selenium测试直接运行在浏览器中,就像真正的用户在操作一样。支持的浏览器包括IE、Mozilla Firefox、Safari、Google Chrome、Opera、Edge等。 适用于自动化测试&#x…...

项目管理-组织战略类型和层次讲解
组织战略类型和层次 对于不同的组织战略可能会采用不同的项目管理形式,组织作为项目管理的载体,其战略决策对项目管理体系的架构,对组织与项目之间责权利的划分具有深远的影响,组织的战略文化也会影响到项目的组织文化氛围。因此…...
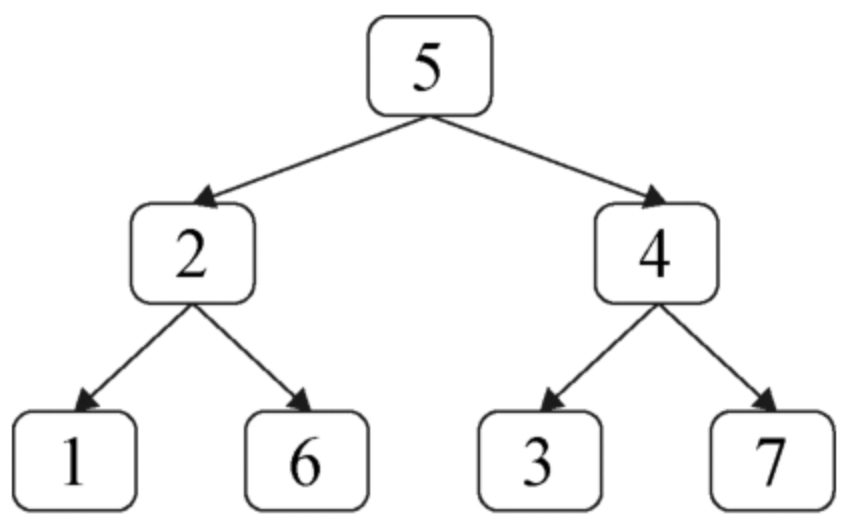
面试算法50:向下的路径节点值之和
题目 给定一棵二叉树和一个值sum,求二叉树中节点值之和等于sum的路径的数目。路径的定义为二叉树中顺着指向子节点的指针向下移动所经过的节点,但不一定从根节点开始,也不一定到叶节点结束。例如,在如图8.5所示中的二叉树中有两条…...

dbeaver查看表,解决证书报错current license is non-compliant for [jdbc]
http://localhost:9200/_license { “license” : { “status” : “active”, “uid” : “b91ae0e0-b04d-4e20-8730-cf0bca7b2035”, “type” : “basic”, “issue_date” : “2023-02-22T14:33:27.648Z”, “issue_date_in_millis” : 1677076407648, “max_nodes” : 10…...
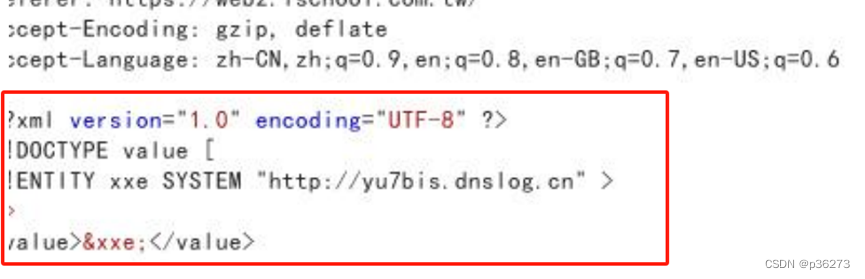
网络安全进阶学习第二十一课——XXE
文章目录 一、XXE简介二、XXE原理三、XXE危害四、XXE如何寻找五、XXE限制条件六、XXE分类七、XXE利用1、读取任意文件1.1、有回显1.2、没有回显 2、命令执行(情况相对较少见)3、内网探测/SSRF4、拒绝服务攻击(DDoS)4.1、内部实体4.2、参数实体 八、绕过基…...
如何将 ruby 打包类似于jdk在另一台相同架构的机器上面开箱即用
需求 目前工作中使用到了ruby作为java 项目的中转语言,但是部署ruby的时候由于环境的不同会出现安装依赖包失败的问题,如何找到一种开箱即用的方式类似于java 中的jdk内置jvm这种方式 解决 TruffleRuby 完美解决问题,TruffleRuby 是使用 T…...

vue封装独立组件:实现分格密码输入框/验证码输入框
目录 第一章 实现效果 第二章 核心实现思路 第三章 封装组件代码实现 第一章 实现效果 为了方便小编的父组件随便找了个页面演示的通过点击按钮,展示子组件密码输入的输入框通过点击子组件输入框获取焦点,然后输入验证码数字即可子组件的确定按钮是验…...

从2D圆形到3D椭圆
要将一个2D圆形转换成3D椭圆,我们需要使用CSS的transform属性和一些基本的几何知识。首先,让我们创建一个HTML元素,如下所 html <div class"circle"></div> 然后,使用CSS样式将其转换成3D椭圆 css .circ…...
Linux CentOS7.9安装OpenJDK17
Linux CentOS7.9安装OpenJDK17 一、OpenJDK下载 清华大学开源软件镜像站 国内的站点,下载速度贼快 二、上传解压 文件上传到服务器后,解压命令: tar -zxvf jdk-xxxx-linux-x64.tar.gz三、配置环境 export JAVA_HOME/home/local/java/j…...
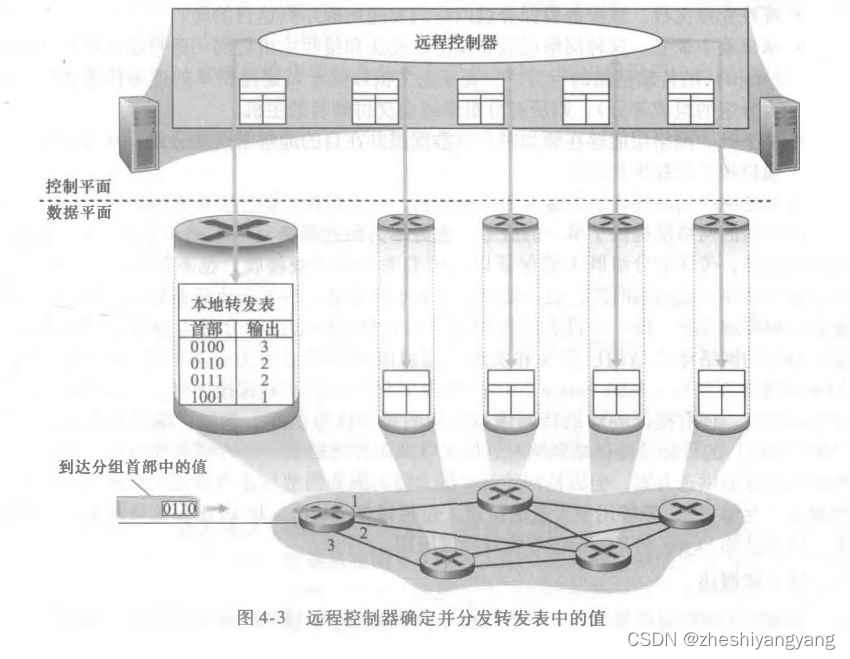
计算机网络第4章-网络层(1)
引子 网络层能够被分解为两个相互作用的部分: 数据平面和控制平面。 网络层概述 路由器具有截断的协议栈,即没有网络层以上的部分。 如下图所示,是一个简单网络: 转发和路由选择:数据平面和控制平面 网络层的作用…...
单元测试学习
回顾测试理论基础 单元测试基础知识 什么是单元测试 单元测试流程、测试计划 测试策略设计、实现 单元测试 - 执行 HTML 报告生成 1 软件测试分类 目标 回顾测试理论知识-测试分类 1. 测 试分类 代码可见度上-划分分类: 1. 黑盒测试 2. 灰盒测试 3. …...

python编写接口测试文档(以豆瓣搜索为例)
📢专注于分享软件测试干货内容,欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢交流讨论:欢迎加入我们一起学习!📢资源分享:耗时200小时精选的「软件测试」资…...

C++查看Class类结构
cl指令 cl test.cpp /d1reportSingleClassLayout 类名 注意。上面指令是d1,1是数字1 , 不是字母l;...

appium如何连接多台设备
我们在做app自动化的时候,若要考虑兼容性问题,需要跑几台设备,要是一台一台的跑比较耗时,因此需要考虑使用多线程来同时操作多台设备。 1.我们拿两台设备来模拟操作下,使用:adb devices查看连接状况&#…...

VUE el-form组件不绑定model时进行校验
在el-form中如果要使用:rules规则校验时,需要在el-form标签绑定 :model 如何不绑定model而进行校验字段: 思路: 1.假设规则为非空判断 2.获取该字段,进行非空判断,记录该字段是否校验完成,添加到校验标识中 3.表单或数据提交时,判断校验标识 required 红星星 :error 提示项 …...

计算机视觉的监督学习与无监督学习
什么是监督学习? 监督学习是一种机器学习算法,它从一组已标记的 合成数据生成器中生成的训练数据中学习。这意味着数据科学家已经用正确的标签(例如,“猫”或“狗”)标记了训练集中的每个数据点,以便算法可…...

Linux-lvds接口
lvds接口 单6 单8 双6 双8...

Android 自定义View一
1.继承已有VIew,改写尺寸:重写onMeasure SquareImageView 2.完全自定义重写onMeasure 3.自定义Layout 重写onMeasure onLayout 1.继承已有VIew,改写尺寸:重写onMeasure 流程: 重写onMeasure 用getmeasureedWidth …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
