数据结构笔记——查找、排序(王道408)
文章目录
- 查找
- 基本概念
- 线性表查找
- 顺序查找
- 折半查找(二分)
- 分块查找
- 树查找
- 二叉排序树(BST)
- 平衡二叉树(AVL)的插入
- 平衡化
- 复杂度分析
- 平衡二叉树的删除
- 红黑树
- 红黑树的定义和性质
- 红黑树定义
- 红黑树性质
- 红黑树的插入
- 红黑树的删除
- B树
- B树基础
- B树插入和删除
- B+树
- 散列查找
查找
基本概念

查找表,其实就类似于数据库的数据表。
所谓的数据项,就是数据库的一列,而关键字就是key,是唯一的。
查找长度(SL)即key的比较次数,ASL是Average SL
线性表查找
顺序查找

基本的查找算法,如果不会写就废了,注意循环跳出条件:key匹配则跳出
哨兵可以简化代码,本质在于,哨兵和普通元素的逻辑是一致的,但是可以发挥出终止的效果
因此,for循环不需要考虑越界,最后return的时候也不需要判断是否查找成功(哨兵本身的0下标就代表失败)
其实链表里的头结点也是一种哨兵。

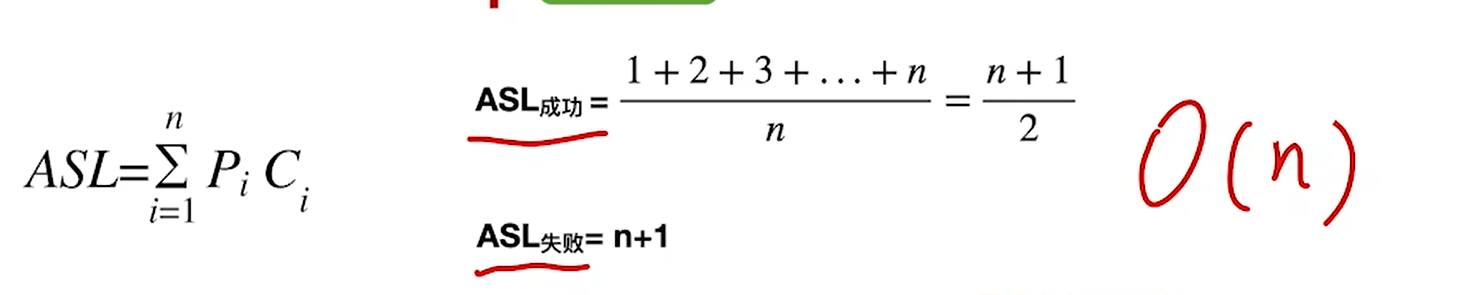
查找的优化思路有二:
- 有序情况下(假定顺序),如果key已经大于目标key了,那么后面也就没必要继续扫了,即
提前终止,可以减少失败ASL - 如果已知查找到的概率,那么可以将高概率的排在前面,即
提前成功,可以减少成功ASL
分析ASL的时候可以用判定树来分析,将判定逻辑写成树,分析ASL的思路如下:
- 成功的ASL,就把n个成功节点加权和,而失败的ASL,就把n+1个失败节点加权和
- 单个成功节点的SL=高度,而失败节点的SL=父节点高度
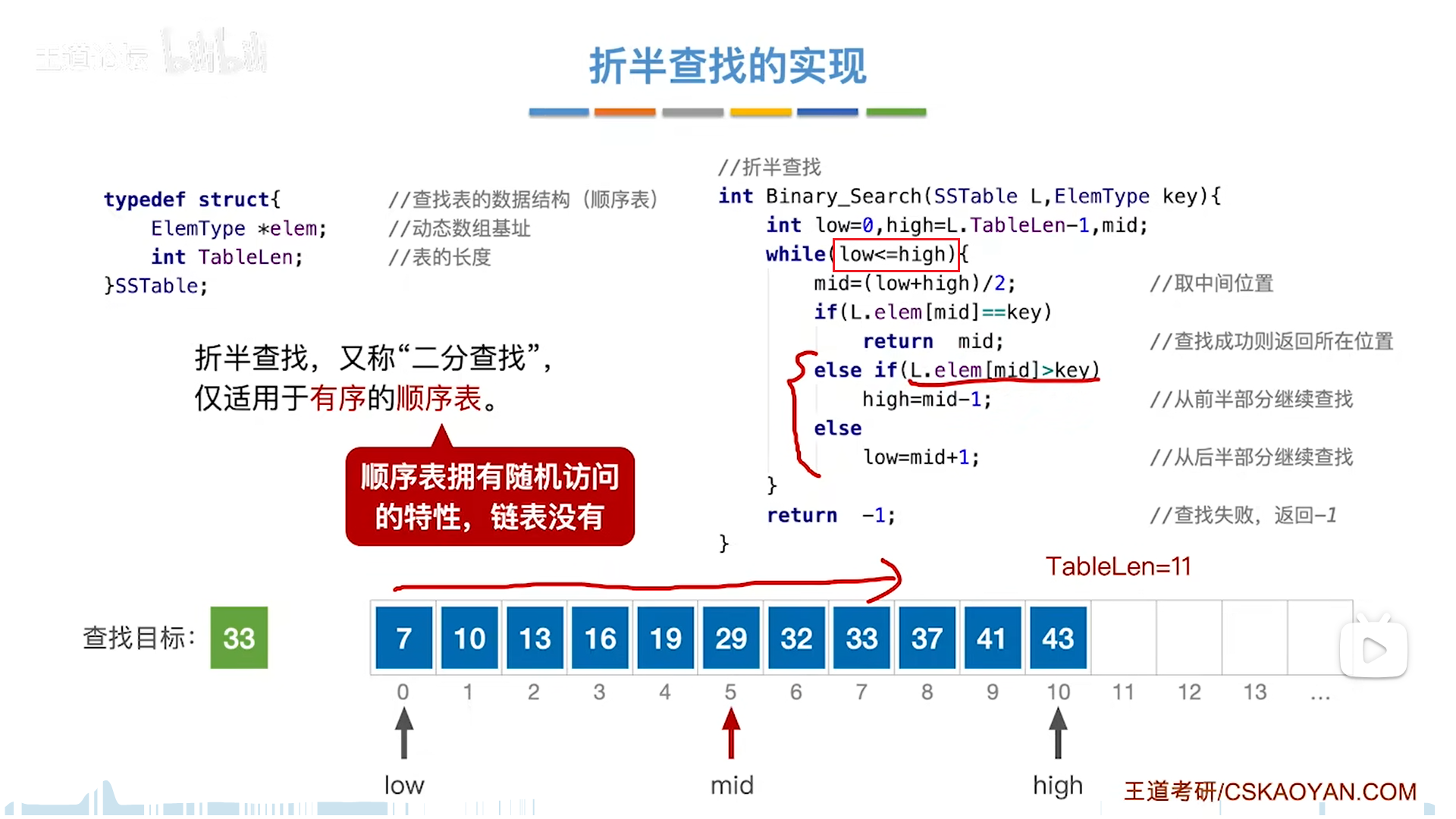
折半查找(二分)
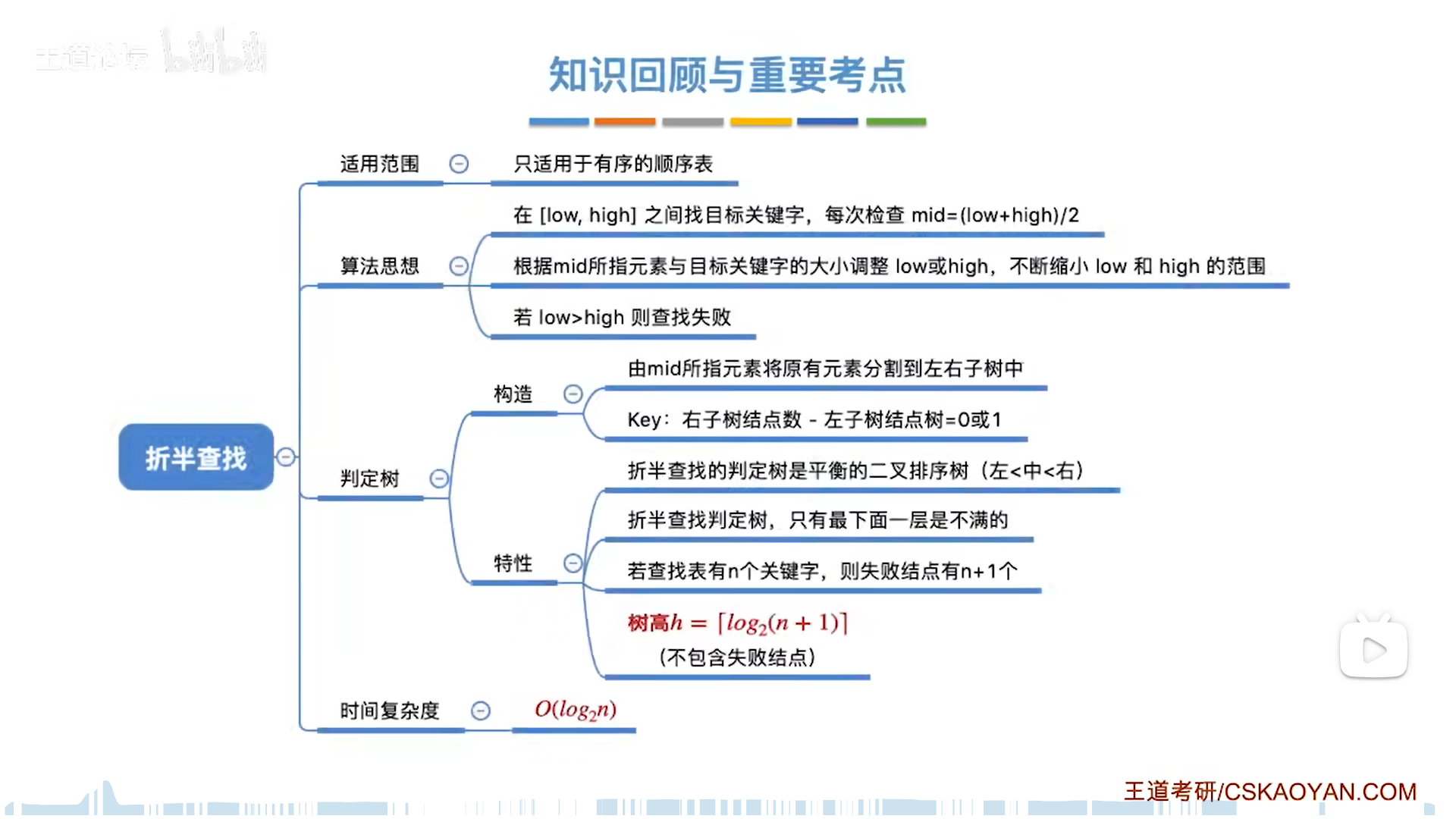
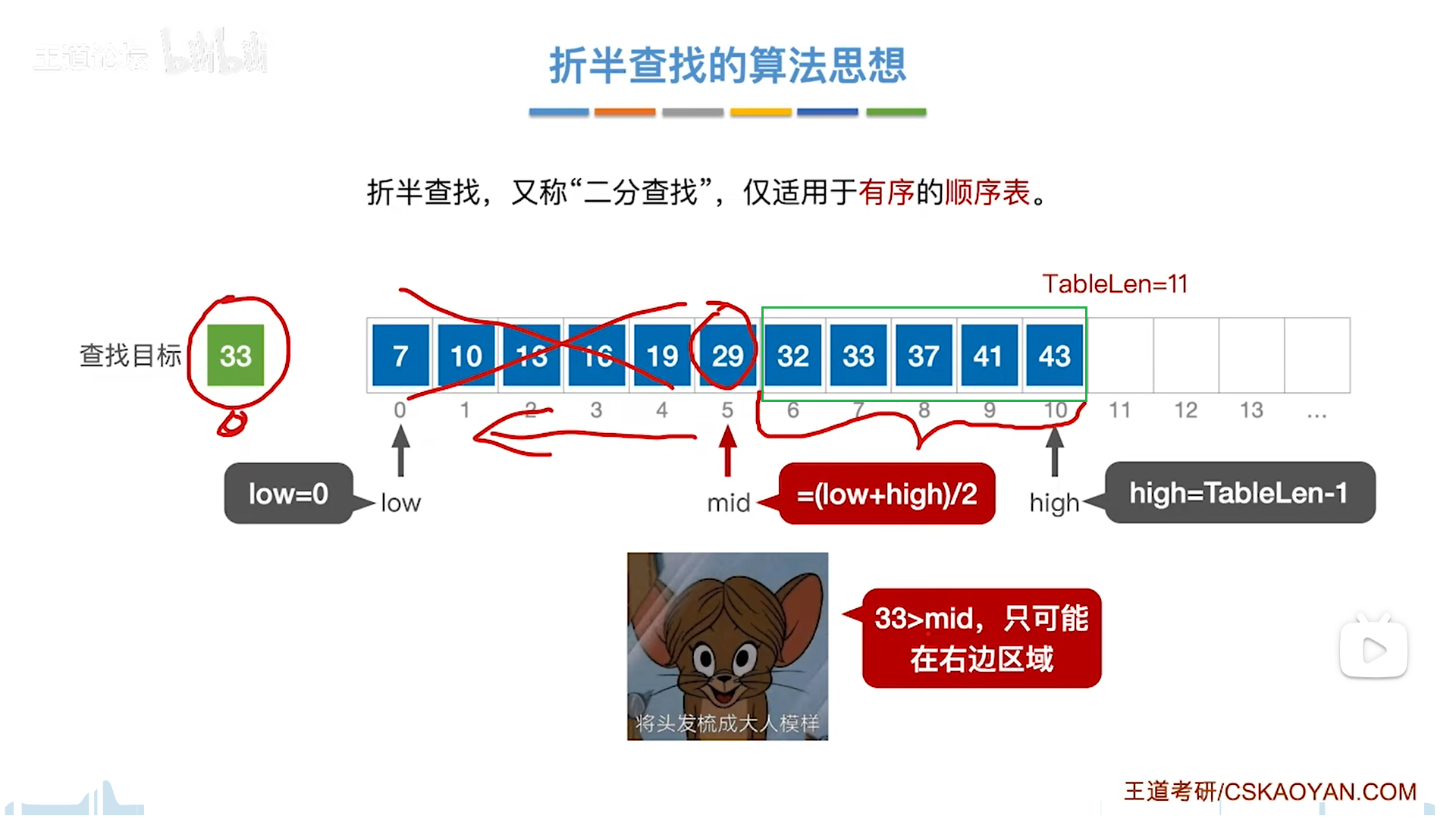
前提是有序。
low和high构成一个闭区间,目标元素只可能在闭区间内,每次要和mid对比。
和mid对比,情况有两大类:
- 等,则成功
- 不等,则代表只能在两侧区域,不包括mid,因此边界要调整为mid-1(小),mid+1(大)
此时你可能会怀疑,最后能不能收敛,如果你是以mid为新边界,下面这种情况可能就无法收敛了,但是如果你去掉mid,即以mid+1为新边界,假设能查到,最坏的情况也一定会收敛到具体的一个点上(此时low==high)
假设查不到,在收敛到具体的一个点后,low和high就要错开,构成low>high的情景,此时直接报错

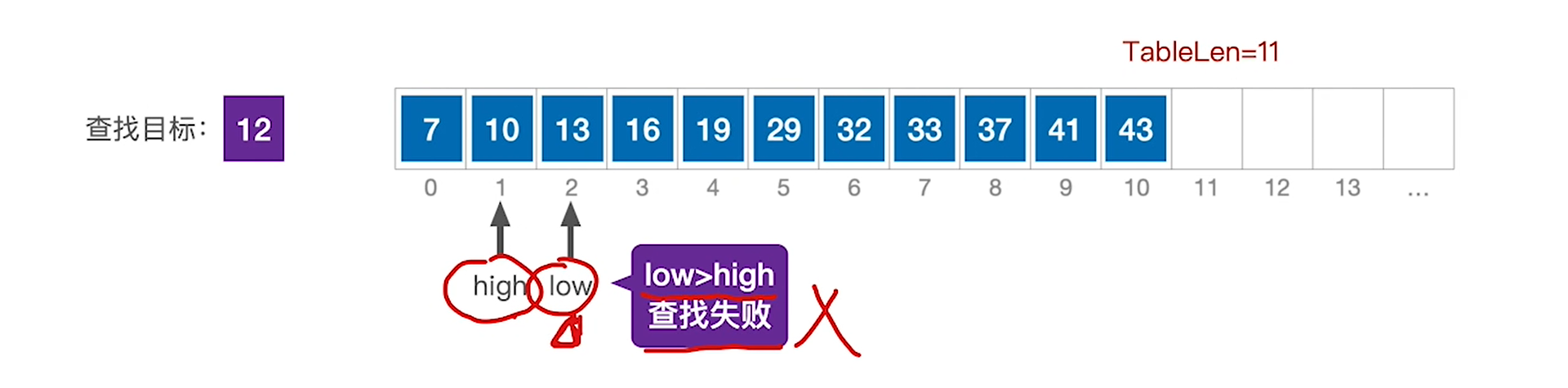
整体来看这个算法,过程如下:
- 考察区域从全部收敛到-1
- 极限情况:low≤high
- 一定会不断收缩,一定可以判定完最后一个点
- 之后继续走的话,low和high会交错,退出循环
- 在收敛过程中,如果成功则提前退出循环
因此这个算法是完美无缺的,可以全覆盖所有可能。
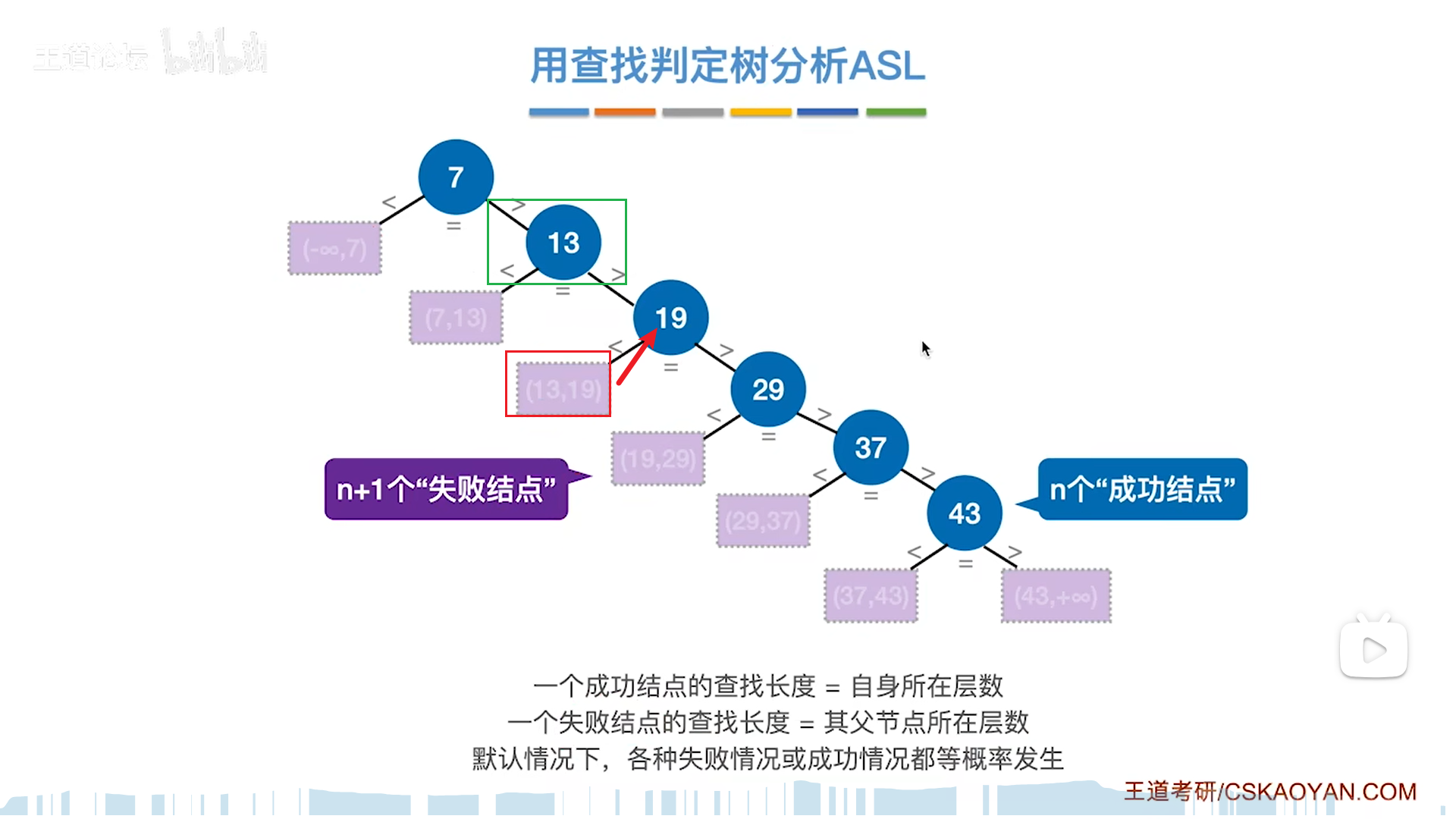
分析效率继续用判定树,这个判定树是非常的神奇好用,把成功节点(mid)逐层展开,再补上失败节点就如下图

需要注意的是,假如总结点数量为偶数个,那么考虑到mid是向下取整,就会出现右子树=左子树+1的现象,不可能更多了,也就是说,右子树-左子树=0或1,只有这两种可能。
反过来,如果mid向上取整,自然就是左-右=0或1
无论哪种方式,折半查找判定树是平衡二叉树,而且只可能有最下面一层不满,那么树高就可以用完全二叉树的算法去算,即log(n+1)向下取整

分块查找
其实分块的最佳储存结构是索引数组+n条链表,操作系统里也会有类似结构出现(比如文件索引)
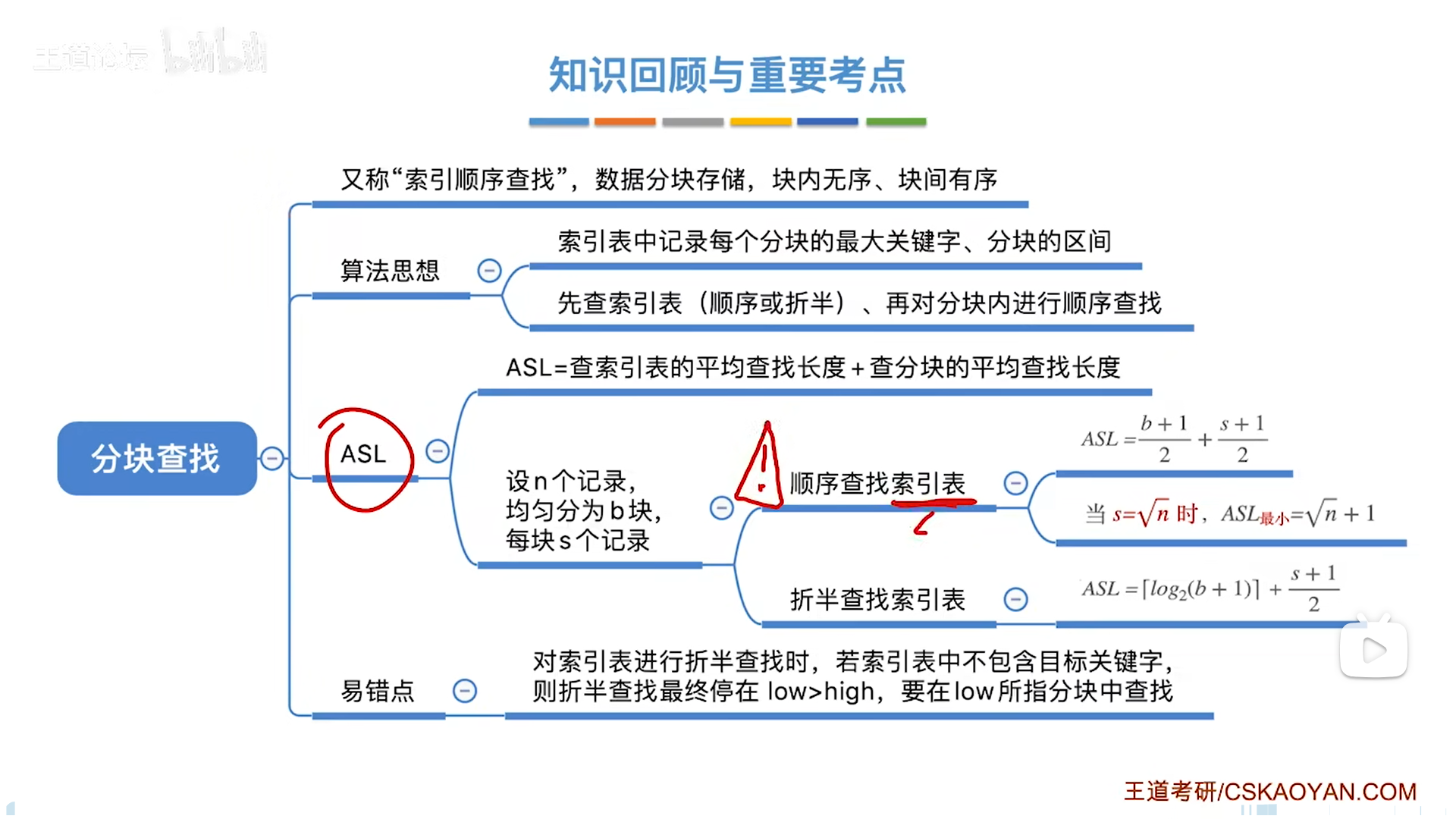
分块查找=索引+顺序,索引用来缩减范围,进而使得顺序查找次数更少
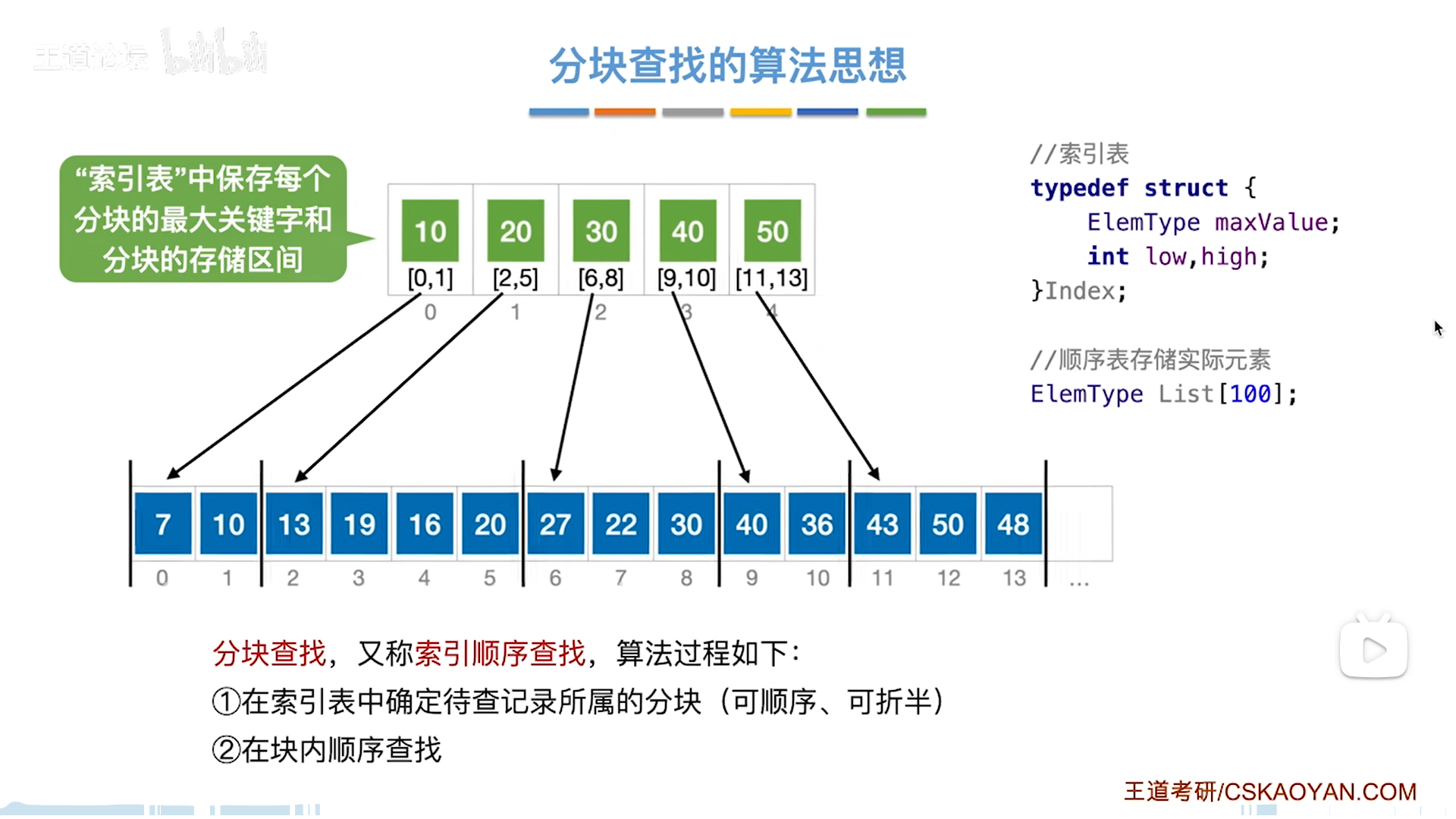
值得讨论的是查找索引的过程。
首先要明白,索引中的maxValue代表索引中最大的值(包括最大),这是后面讨论的基础:
- mid=key,这种情况其实比较少见
- mid≠key,则最终一定会停在low上
- 最终high在左,low在右
- 因为low左边都是小于目标key的,根据前面maxValue的意义,索引的值都小于key了,那必然不存在,所以low左边是不可能的(太小),而low右边又太大了,那么最后就会卡在low上
- 假如low越界,代表所有索引对应的块都不可能存在目标key

对于每一个节点,其SL=索引查找次数+顺序查找次数
需要注意折半情况下的索引查找次数,分析起来比较复杂,假如key≠mid,那么最后就要反复调整直到high<low的时候,这才是真正的索引次数。
因为SL有两部分,而且相关联,所以算ASL比较麻烦,为了便于分析,直接把数组等分,那么这两部分的关联性就打破了,可以分别计算ASL1和ASL2,最后相加。

具体分析,顺序情况下,n=sb,因此把b=n/s带进去ASL就可以得到一个式子,进而求得极限情况的ASL
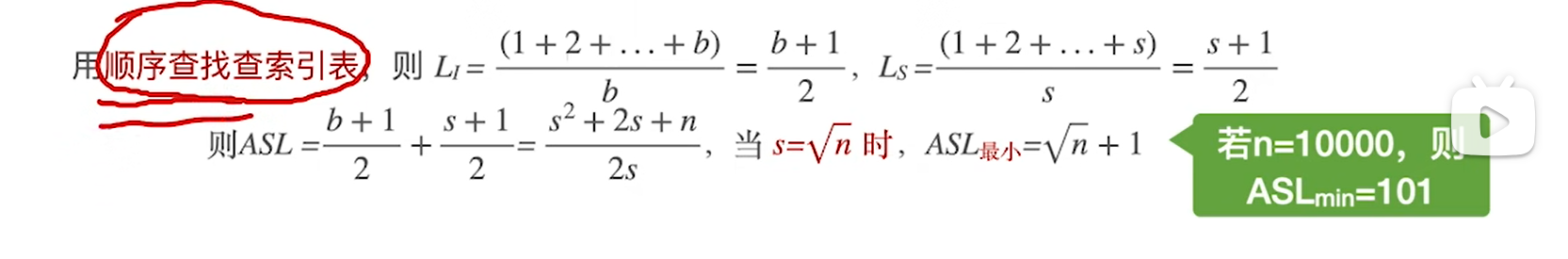

其实这才是最完美的索引顺序结构。
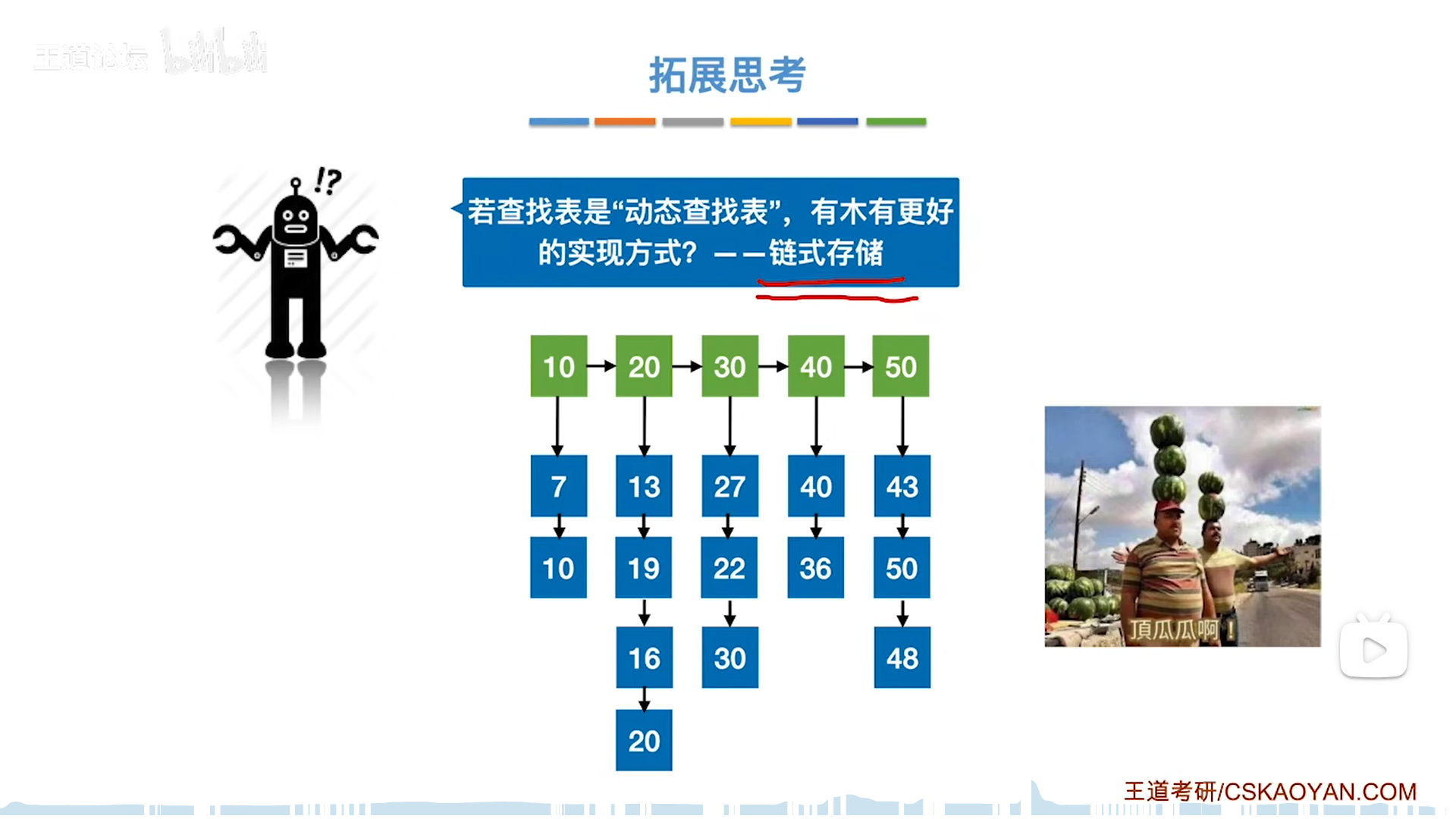
树查找
二叉排序树可以说是,带有伸缩功能的顺序数组,只是说不平衡会导致其效率退化
而进一步的AVL树,弥补了不平衡的问题,在保证伸缩性的前提下,最大化逼近数组的效率
可以说是比较完美的结构了。
二叉排序树(BST)
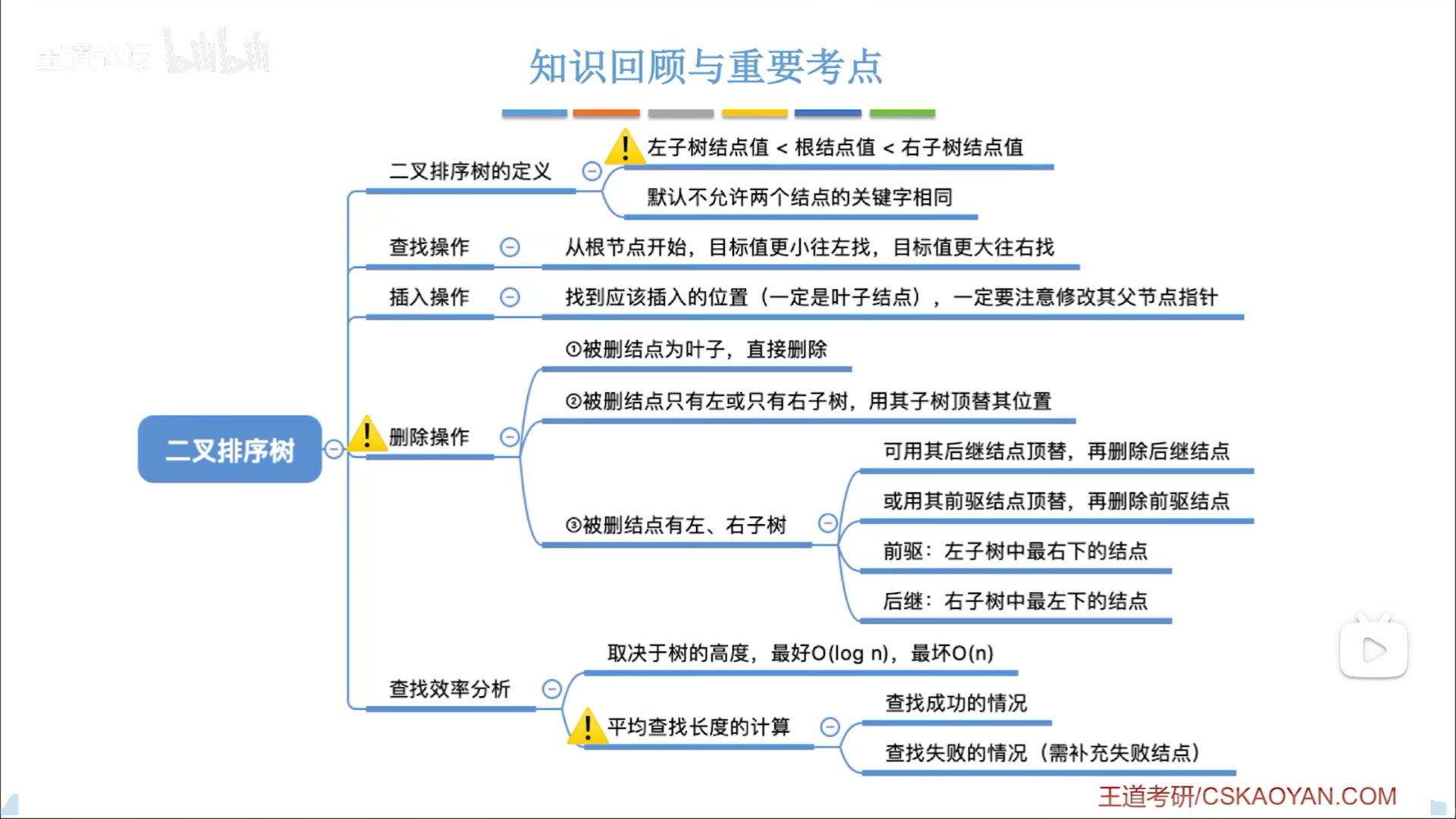
递归和循环的思路一样:
- 退出条件:空,或者匹配到
- 否则就查左/右子树

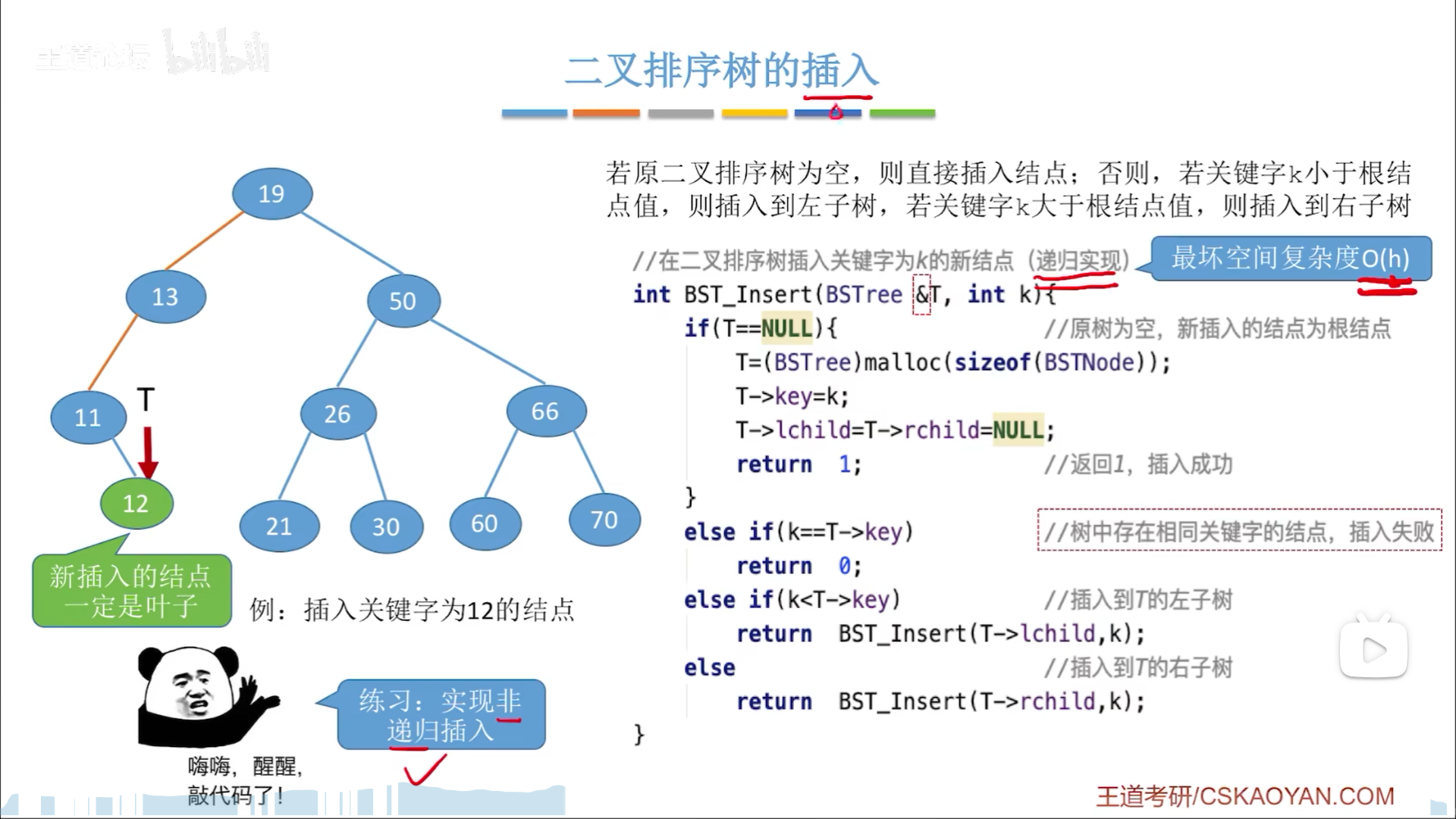
插入,就是要找到插入点位:
- 有一样的,失败
- 没有一样的,生成新节点,令父节点链域指向该节点。
- 父节点指针从何而来?需要注意BSTree &T,也就是说,在最后T==0的时候,这个T不仅仅是空指针,其本身还是父节点的孩子链域,因此我们直接把T指向新节点就可以了,在第一步就完成了。
- 记得初始化左右孩子为NULL
有了插入后,给定一个T=NULL的初始链域,就可以反复插入,形成二叉树。
删除节点,这个涉及到树结构的重构,比较复杂:
- 叶子结点
- 只有单边孩子
- 有双边孩子,按照中序序列,上层是左根右,展开后变为(左根
右)根(左根右),删去根后有两种顶替思路- 以右子树最左边的节点顶替根(大中最小),那么拆掉的这个节点又该怎么补呢?恰好最左边的节点,一定不可能有左子树,这就划归到了2情况
- 左侧情况反过来就行

查找效率用ASL评估,这俩在查找中是等价的。
给定具体的一个例子,成功的ASL则要去计算n个成功节点的加权,而失败则要补n+1个失败节点,再加权
下图表示,二叉树查找的平均效率与其高度成正比,那么理想情况是把高度压制成平衡二叉树,这就是后面的内容了。

平衡二叉树(AVL)的插入
平衡化
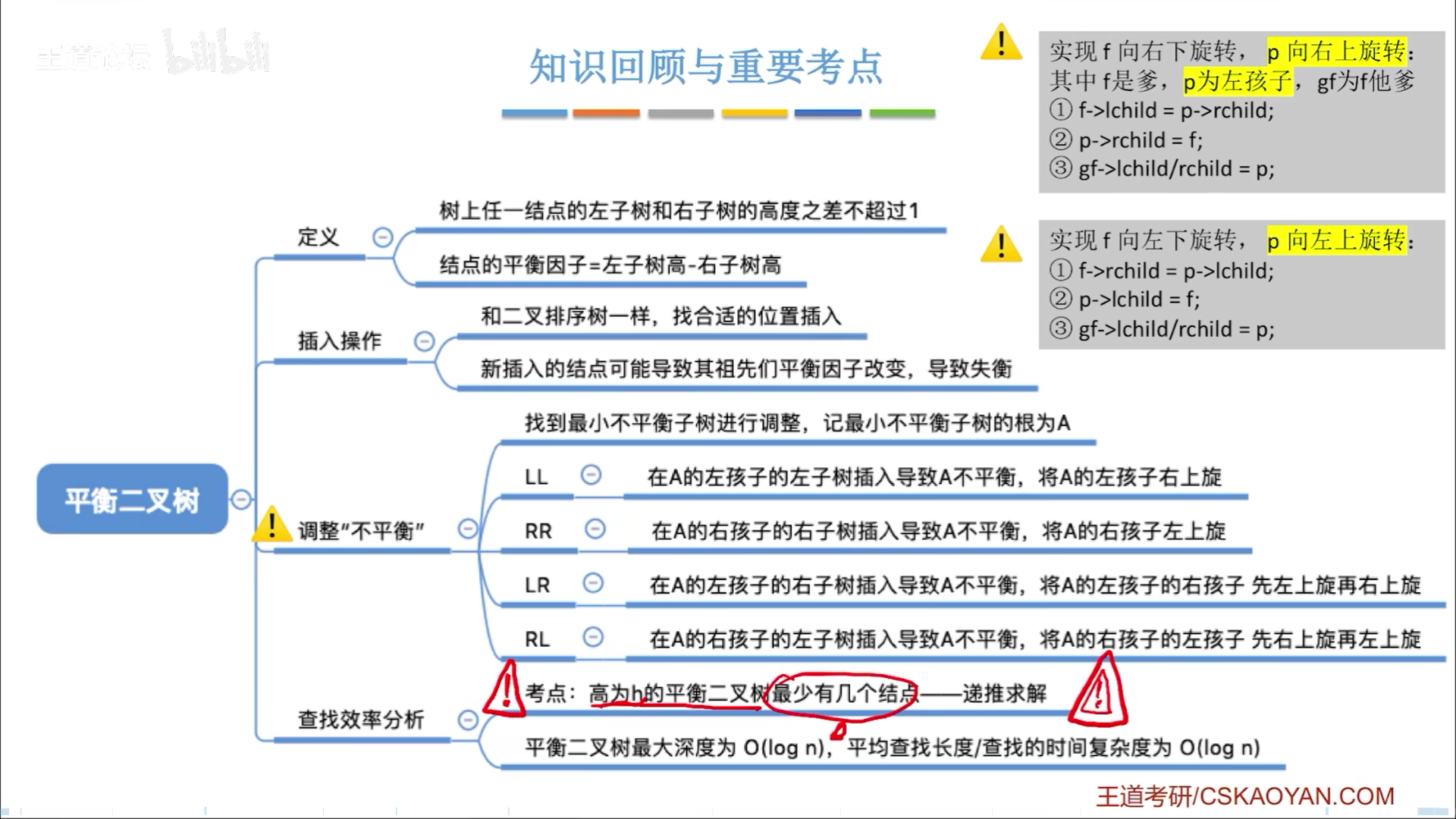
平衡二叉树,任一节点的平衡因子(左-右)都只可能是-1,0,1,如果添加节点导致破坏平衡性,就要找到最小不平衡树,进行平衡化修正

以最小不平衡树根节点为A,则不平衡无非就是四种情况,LL,LR,RL,RR,这四种情况的记忆方法如下:
- 第一个字母代表A的左右子树
- 第二个字母代表子树的左右孩子
因此LL就是左子树左孩子插入,导致不平衡,到时候自己画图就好。
首先要说明,三个子树都是H高度,这个是铁定的,否则插入就不会破坏平衡性。
LL和RR比较简单,本质在于让B当根节点,因此转一下就行
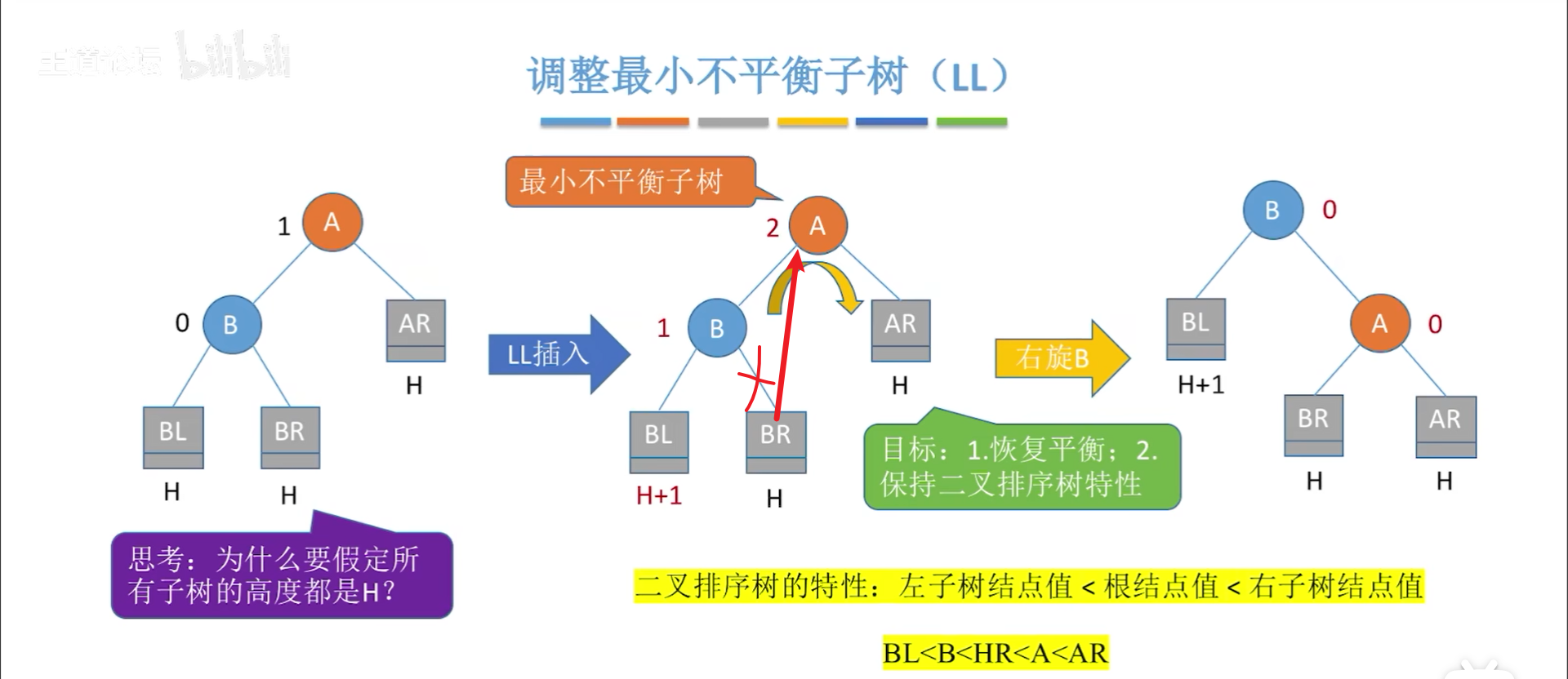

看下操作,实际上是要让B当根,A当孩子,因此分三步,写旋转代码要按这三个步骤来:
- 替换A的左孩子,此时A成为一颗可以随意挪动的树
- 让A成为B的孩子
- 让B成为根节点

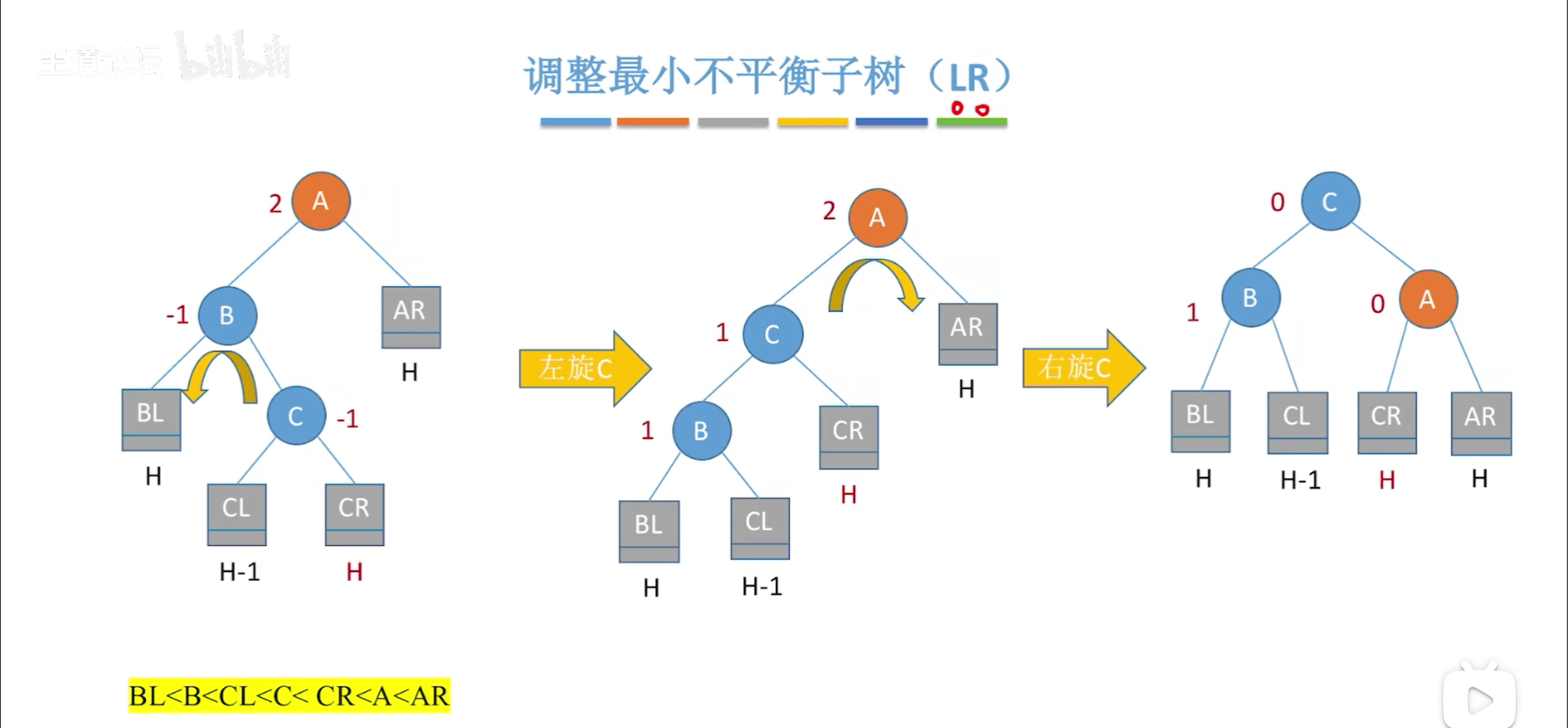
LR和RL复杂一些,对于LR,具体还要把L子树的R孩子(高度为H+1)继续展开,以便于分析,但是实际上,这两种情况是一样的,因此假定是下图情况。
但是实际上本质不变,最终的目标是让C当根节点,BA分别为左右,那么C就要转两下,先和B在和A,这样C就可以变成根节点,两次旋转沿用前面的思路即可。
RL也是如此,最终要让C当根节点。


最后再整体总结一下,你会发现4类情况,最小不平衡子树本来都是H+2高度,然后插入新节点变成H+3,破坏平衡性,调整以后重归H+2,同时平衡性保持住了
之所以只调整最小不平衡树就可以保证整体平衡性,是因为这一通调整将多出来的高度抹平了,更上面的节点的平衡因子自然就退回到平衡状态了。
我们把眼光落实在做题上:你要盯一眼,从下往上找到第一个不平衡的节点,代表最小不平衡树的根节点,然后回忆4种情况,标上ABC,剩下步骤就很简单了,如此就秒杀了。

复杂度分析
无论是插入还是删除,费时间的其实还是查找目标位置,说白了ASL和查找是一样的,调平衡度不影响。
再有就是复杂度分析,ASL=层数,即O(h)效率,关键在于如何通过节点数量n计算h的上界(或者通过h计算n的下界)
这是个数学问题,根本在于AVL的特性,即平衡因子最多为1,那么极限情况就是高度为h的树,一颗子树高度为h-1,另一颗为h-2,因此这颗树的节点数 n h = n h − 1 + n h − 2 + 1 n_h=n_{h-1}+n{h-2}+1 nh=nh−1+nh−2+1=左子树+右子树+根
考虑初始情况,高度为012,最少节点也是012,按照递推就可以计算出任何高度的节点数下界。
反过来,已知n,就可以知道h上界
最后算ASL,经过一通推导,结果就是O(logN)

平衡二叉树的删除
第一步是按照二叉排序树删除,这一步本身就挺麻烦
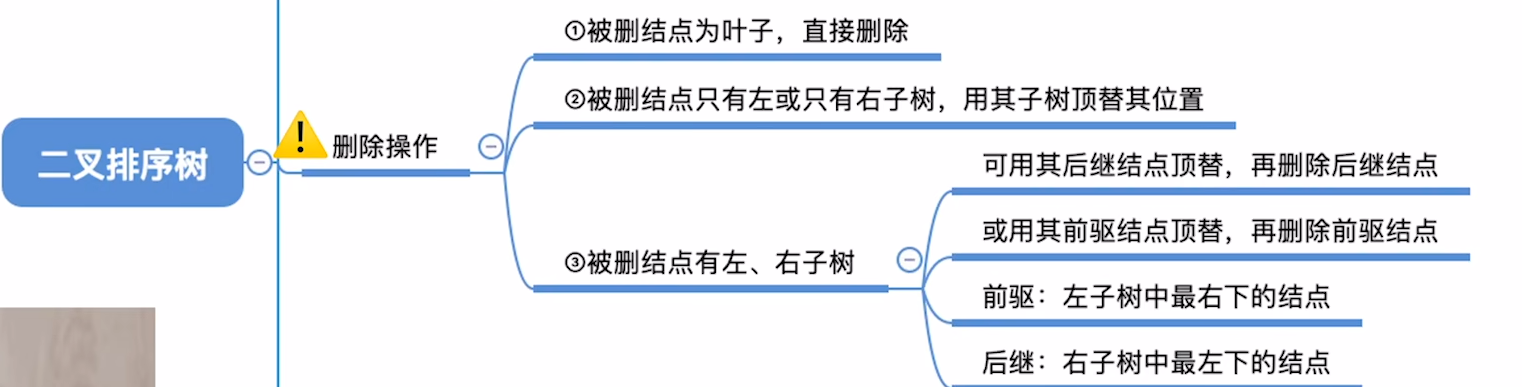
先看一个简单的例子,熟悉流程
- 从删去点向上找,找到第一个不平衡节点,这就是最小不平衡树的根
- 从根开始,找个头最高的儿子和孙子,其实就是从上往下,找到不平衡的传导链条
- 判断4类不平衡情况,进行旋转
- 这一步可以使得不平衡部分的H减小1,这样可能会导致树的另一侧过高失衡,要二次调整,回到1步开始
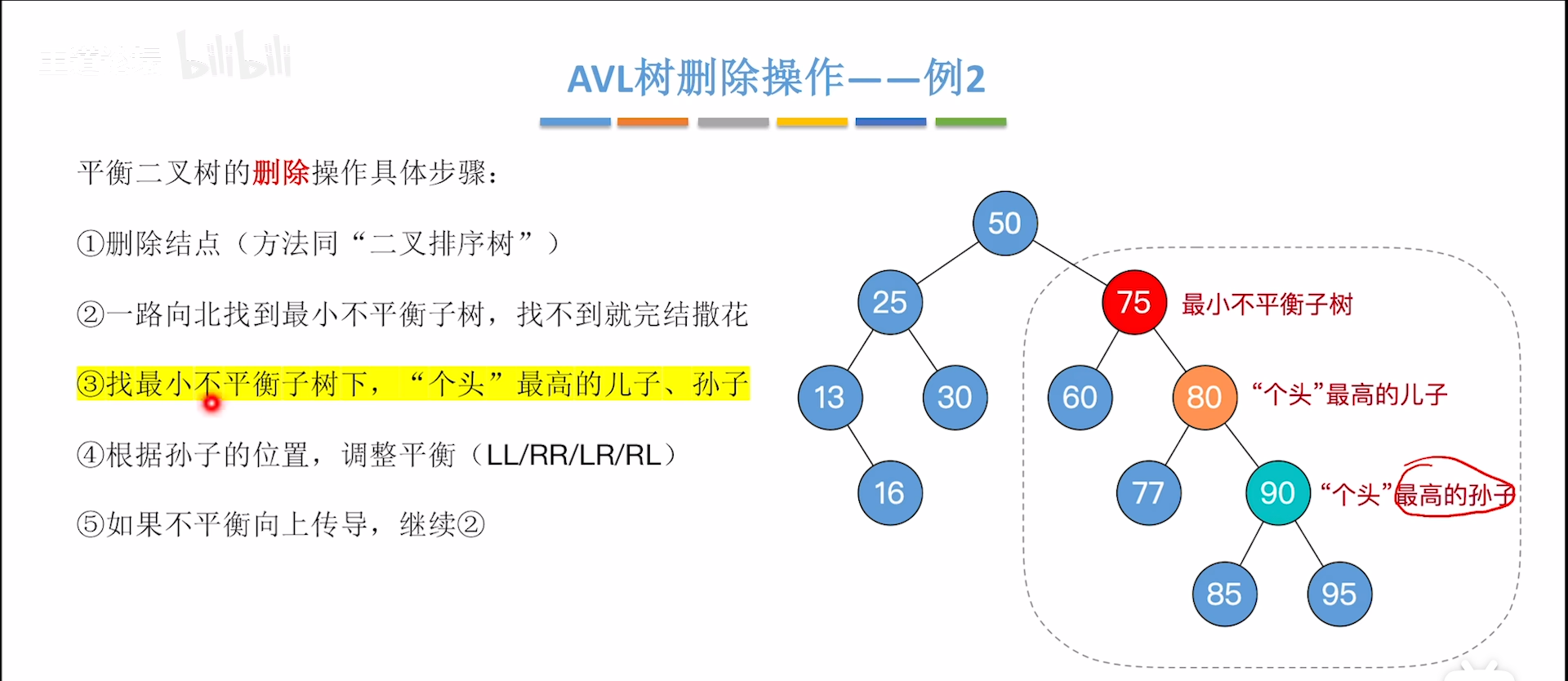
接下来举一个需要二次平衡的例子,下图进行第一次平衡后,右子树高度减一,导致左子树太高。
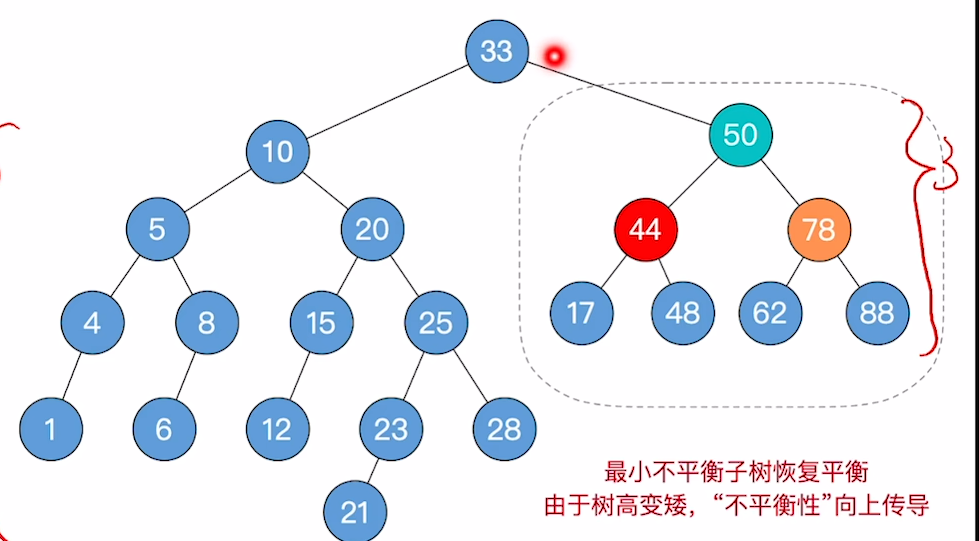
跳回到1步:
- 从调整点位开始向上找,找到第一个不平衡点,即33
- 然后从根节点开始向下找不平衡链条,为33-10-20
- 进行翻转,即可平衡
有没有可能出现第三次不平衡?有可能,因为我们这次找到根恰好也是整个树的根,因此一步到位,假设我们找到的根上面还有东西,那么这一层降低高度后还有可能导致另一侧失衡,总之是一定要向上找是否失衡

考试中可能出现的最极限的情况是,删除的节点同时有左右孩子,那么这个时候就有两种删除方案。
后面仍然按照我们的流程来进行调整
但是这其实就有歧义了,408不太可能出这种,最后提一嘴,复杂度同查找,O(logN)

红黑树
红黑树的定义和性质
虽说AVL的复杂度是logN,但是实际上,每次找最小不平衡树比较费时间,实际消耗时间会有一个常数级别的放大,如果要频繁改变结构,就比较慢,红黑树应运而生。
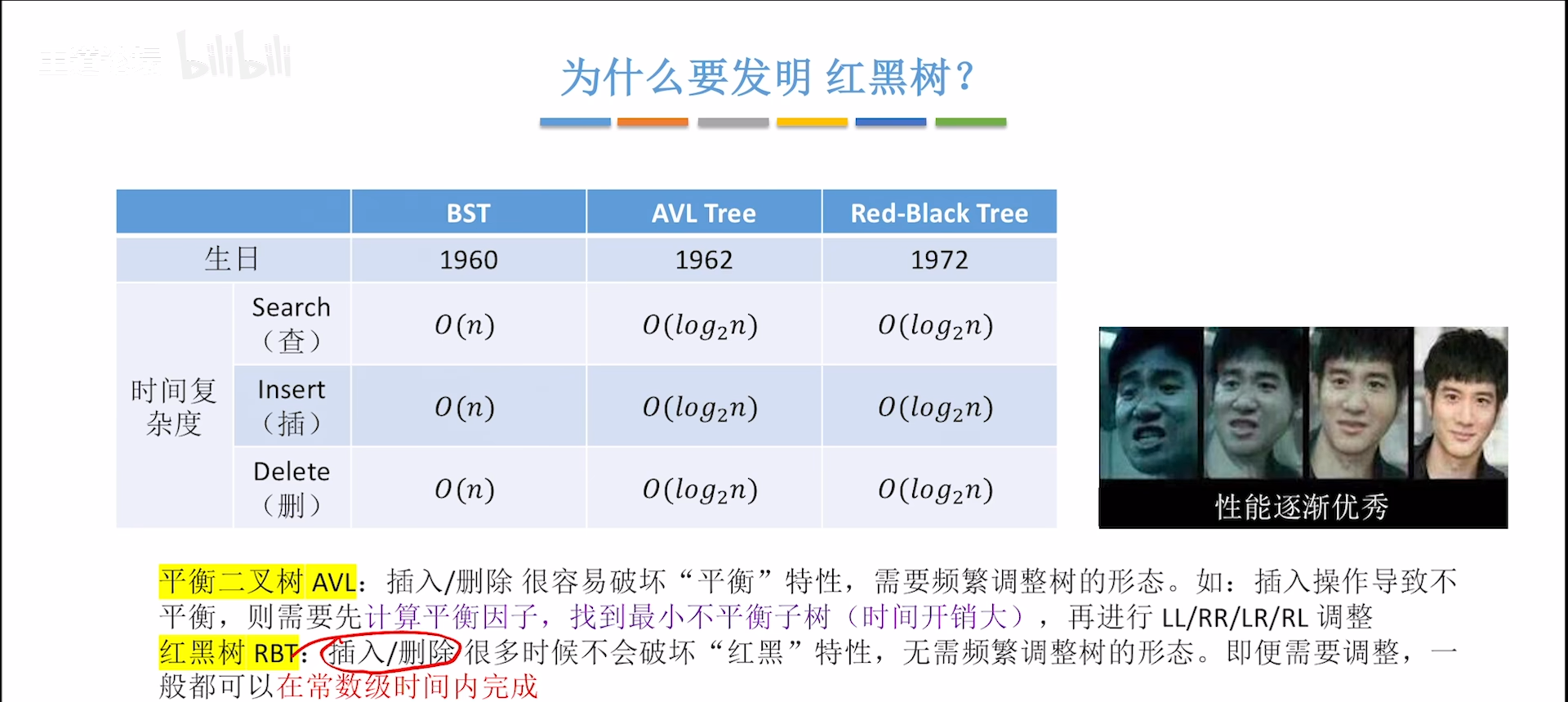
首先明白,红黑树是从BST,AVL一脉相承过来的,所以本身也具有BST性质:左<根<右
或者说,AVL和红黑树都是BST的改进,AVL和红黑树严格来说是并列关系,但是性能是要碾压的
红黑树相比于BST来说,有两点改变:
- 使用三叉链表结构
- 增加了节点的红黑特性(对标AVL的平衡因子,但是有所不同)
红黑树定义
多出来的两个信息,可以为操作带来诸多方便,理解一下下面的规律:
- 左根右。这告诉我们红黑树的本质还是BST
- 根叶黑。根节点和叶节点都是黑色的
- 叶节点并不是我们传统意义上的叶节点,而是代表(外部,NULL,失败),这三个说法是等同的,也就是我们之前判定树计算失败ASL时补上的节点。
- 与叶节点对应的就是内部节点,就是有具体意义的节点,可以成功的节点。
- 不红红。不存在相邻的红节点
- 这是对红节点的限制,但是黑节点无所谓,可以相邻
- 黑路同。任意节点(不一定只是根节点)到任一叶节点的通路上,路过的黑节点数量相同
- 这是对黑节点的限制,同理红节点无所谓

一个基本功就是判断红黑树是否符合定义,大致思路如下:
- 根叶黑。先看根节点和叶节点
- 不红红。扫一眼看看有没有红节点相邻
- 黑路同。这个就比较复杂了,你在看一眼黑色聚集的比较多的地方,那些地方极有可能会出现黑色路径过长,黑节点太多的问题
- 左根右。这个也
容易埋坑,你要知道红黑树首先是一颗BST,所以如果出题很阴,会出在这里。

下面这道题很阴,看哪个7,好在这种情况一般是出现在前三条都失效的时候,此时选择题里估计最多剩俩选项,硬着头皮细心对比就行

红黑树性质
性质清单:
- 黑高定义,h
- 给定h,内部节点下界
- 给定h,内部节点上界(红节点上界)
- 最长路径最多是最短路径的两倍
- 给定n,设H为总高度(非黑高),则高度上界 H ≤ 2 l o g 2 ( n + 1 ) H≤2log_2(n+1) H≤2log2(n+1)
前面铺垫一大堆,都是规定,通过这些复杂的规定,可以产生很多有趣的性质,这才是红黑树高效率的开始。
首先从“黑路同”里衍生一个概念:
黑高,即从这个节点开始,走到任意一个叶节点经过的黑节点个数(不包括自己)
根据黑路同逻辑,一个节点的黑高一定是一个具体的值,从一个特定节点开始,无论是从那条路走,黑高都是一致的,因此用统一的值描述。
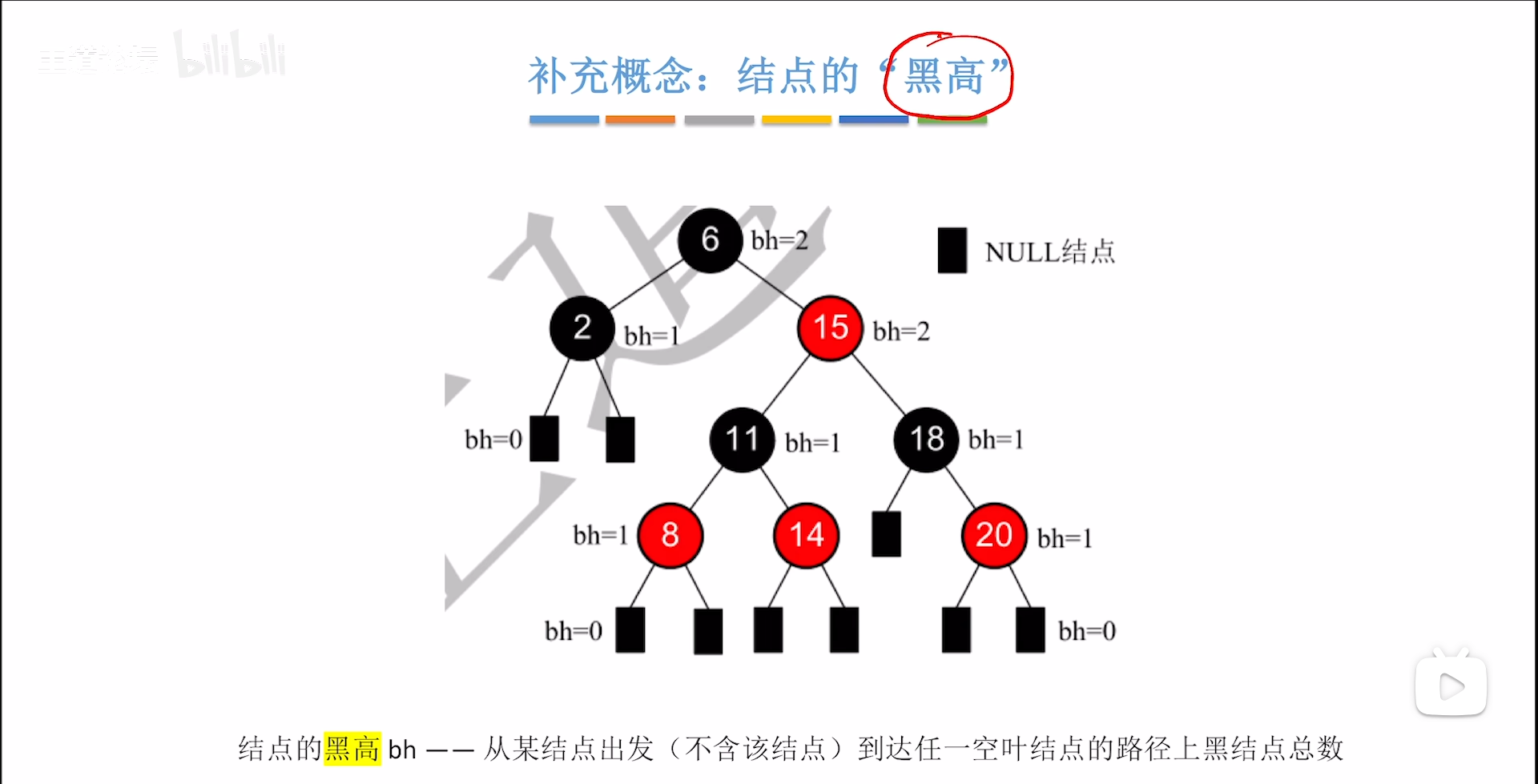
其实我们更深地考虑一下,黑路同这个特性很好玩,如果不考虑红节点的话,纯黑情况下一定是满二叉树,黑高就是内部节点的层数,因此黑高为h的红黑树,内部节点至少是 2 h − 1 2^h-1 2h−1

而红黑树是什么东西呢?其实就是在一个满二叉黑树之间,尽可能塞入不重复的红节点,那么给定黑高为h,极限情况下,可以塞入 2 h + 1 − 2 2^{h+1}-2 2h+1−2个红节点,
这个的计算如下图,给定h为黑高,算上最顶上的那个×,总共可以塞h+1层红节点,即 2 h + 1 − 1 2^{h+1}-1 2h+1−1个,然后你再去掉顶部×这个不能加的节点,因此就是-2
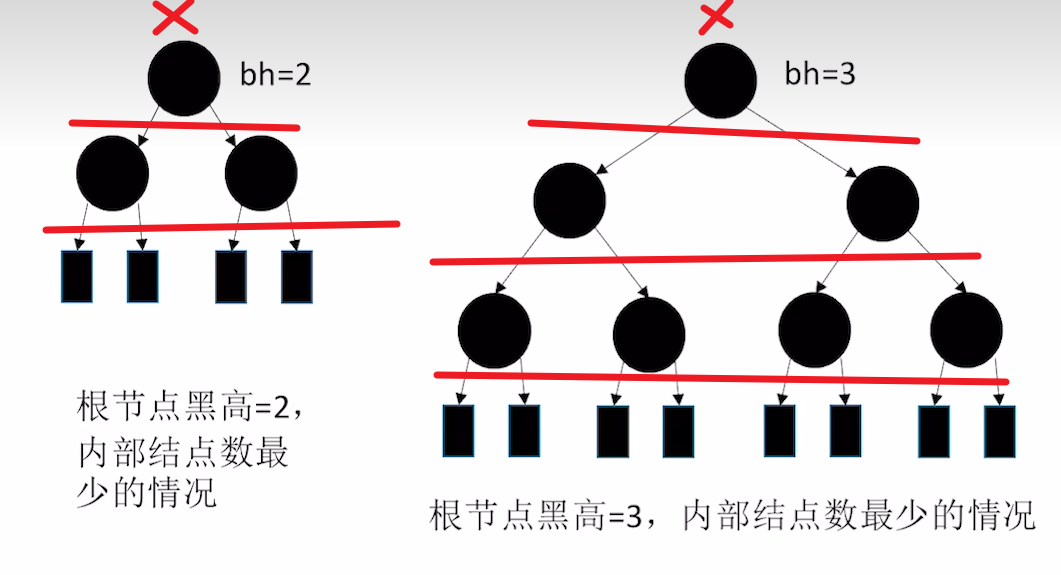
其次再论两个性质:
- 根节点到叶节点的极限路径长,最多为两倍关系
- 最短路径为纯黑
- 最长路径为从黑(根节点)开始:红-黑-红-黑,实际上路径就是一红一黑,插入尽可能多的红节点,也就是最短路径的两倍
- 给定内部节点N,则极限高度为2log(N+1),因此查找操作的ASL和AVL一致


红黑树的插入
如何构建一颗红黑树?
或者说如何在插入的时候保持红黑特性?
这就是本章研究的问题
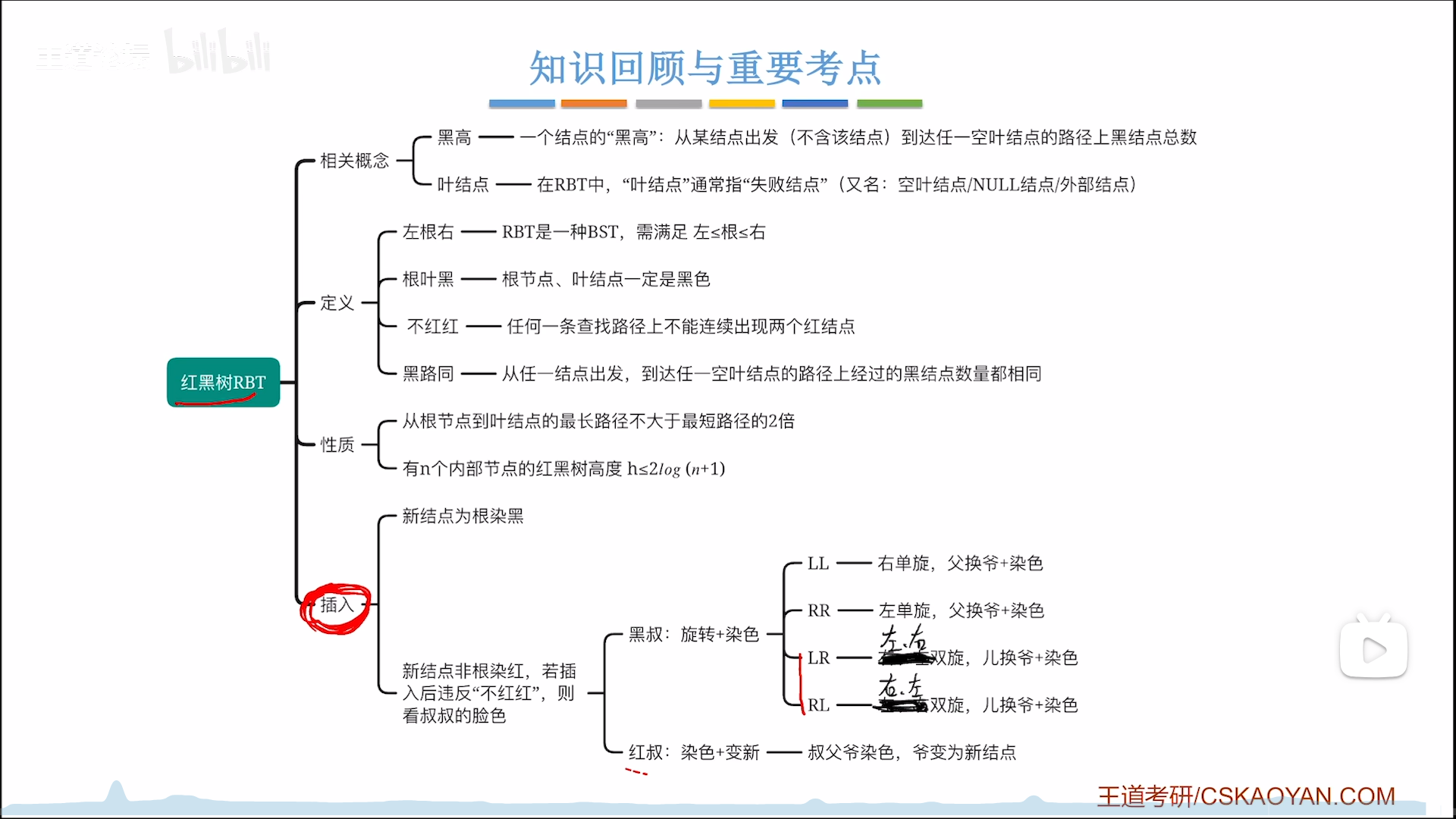
插入一个节点操作如下:
- 根节点染黑,根叶黑
- 非根节点染红,能够保证黑路同
- 可能不平衡,1,2条可以保证根叶黑,黑路同,而找节点的过程也满足BST特性,因此唯一可能不满足定义的地方就是红节点连续,而且不平衡只可能在非根节点时候发生
- 因此不平衡=红节点连续,调整要看
叔 - 叔黑,旋转+染色
- 首先要找到旋转的极大不平衡根节点,从下面插入的儿往上,上层为父,上上层为爷,爷其实就对应AVL里面极大不平衡树的根节点
- 对于LL,RR型,父爷换,之后令交换的两个节点反色
- 对于LR,RL型,把儿换到爷位,之后令交换的两个节点(爷儿)反色,父节点不反色
- 叔红,反色+判新(不用调整结构)
- 反色部分为父叔爷,其实就是把
上面两层反色 - 判新,指把爷当做新节点,跳到第1步
- 反色部分为父叔爷,其实就是把

下面这个例子是:不平衡+黑叔+LL/RR型,先单旋再反色
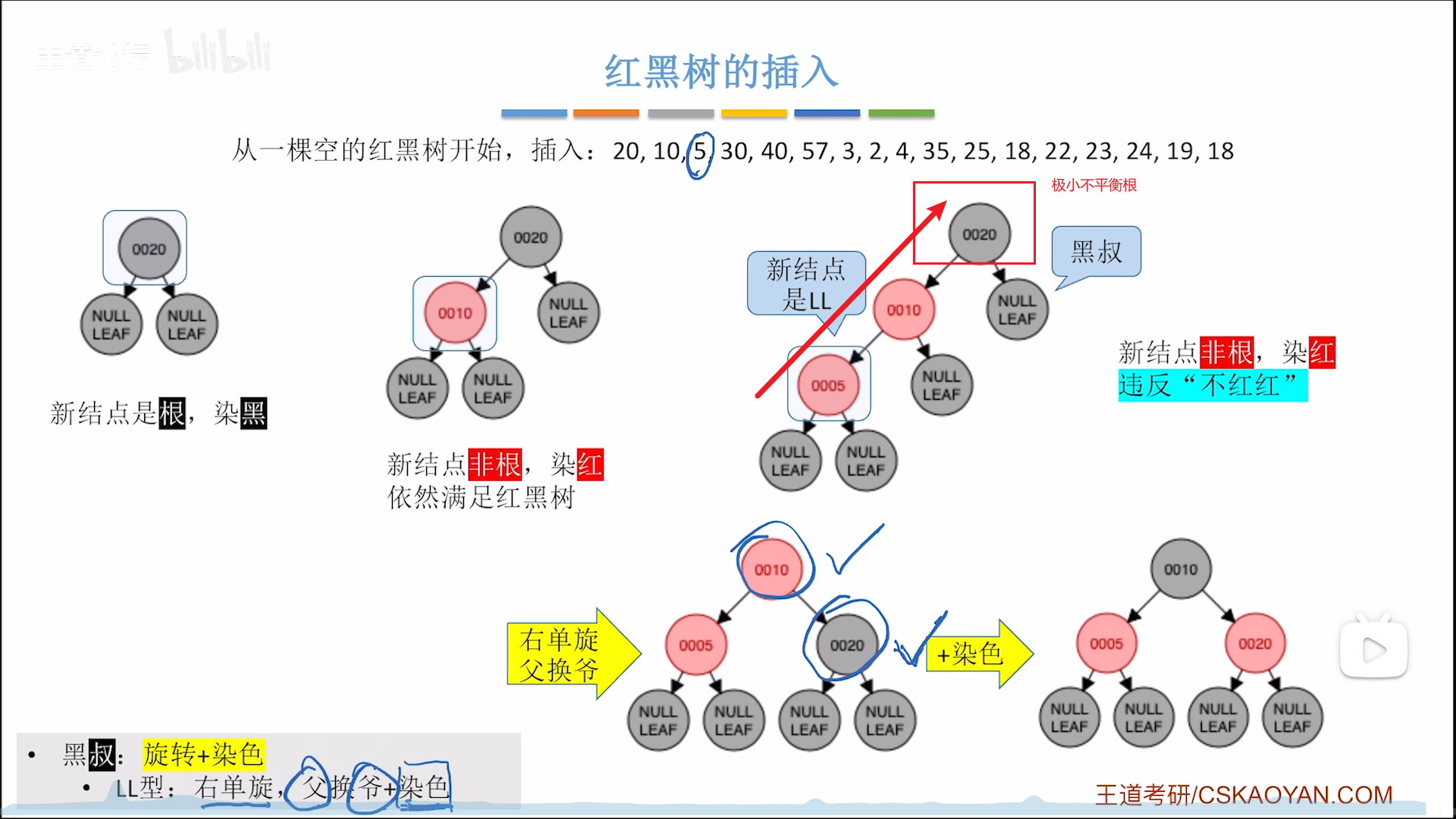
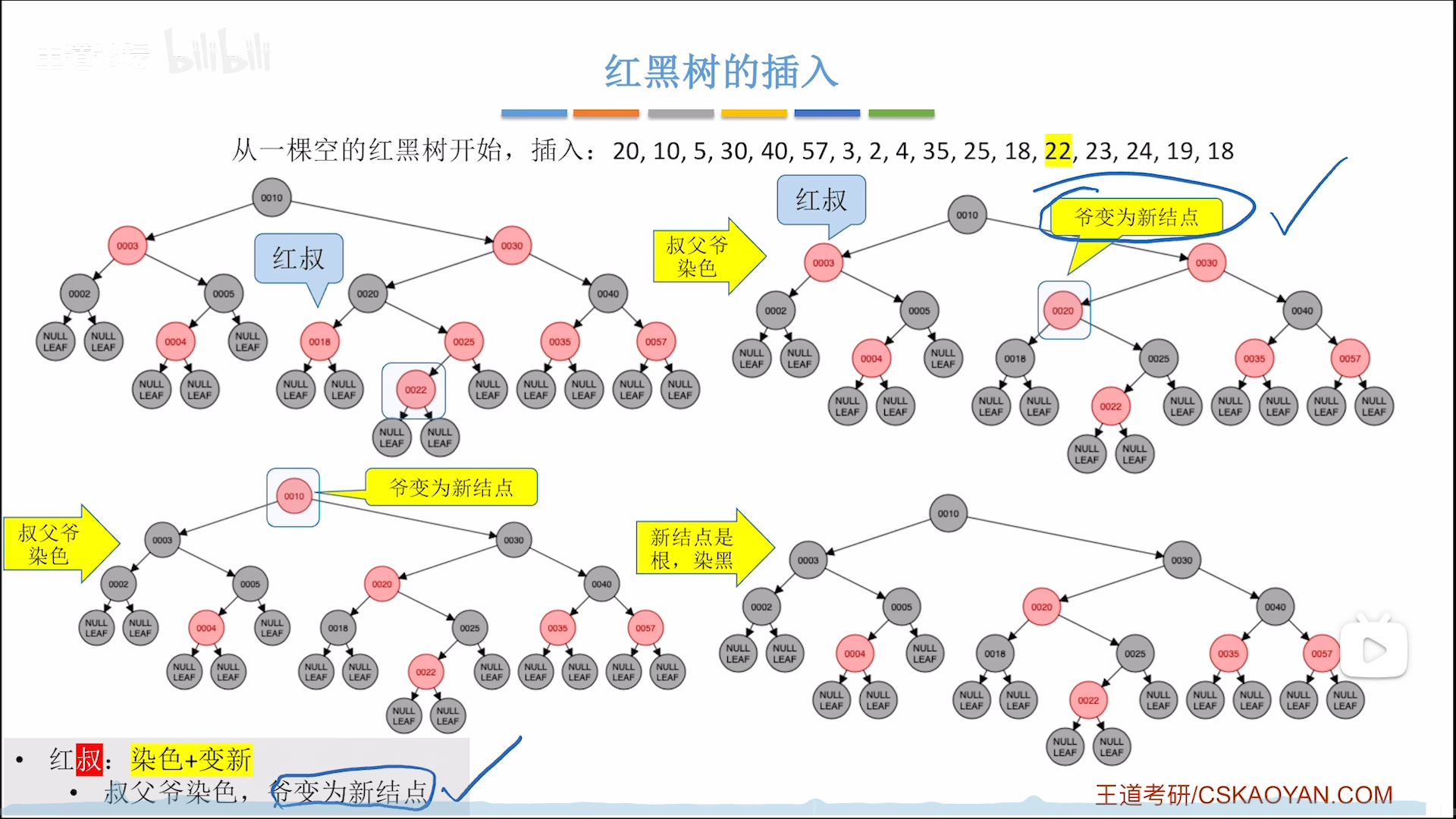
下面这个例子是:不平衡+红叔,则反色上两层
然后以爷为新节点,再判断一轮,此时为:根,染黑
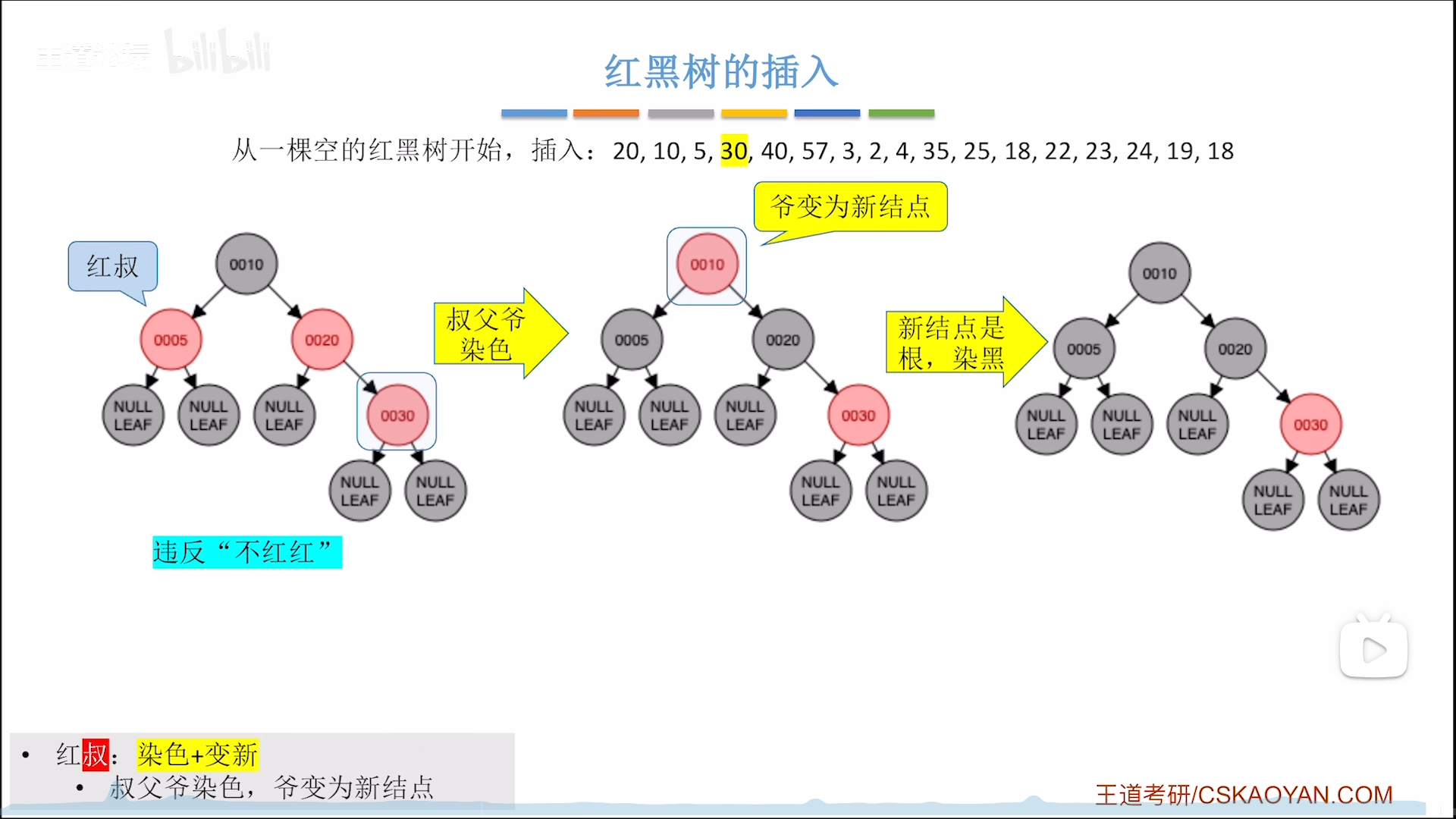
当红黑树逐渐变大,你会发现红黑树有一个有趣的特性,就是大部分情况下是不需要调整的(其实AVL和红黑树的最终目标都是平衡,那么AVL其实也差不了太多,关键在于AVL需要去向上找最大不平衡根,而红黑树的爷就是最大不平衡根,寻根效率更高,这才是红黑树碾压AVL的本质)
下图是一种连锁反应,这种连锁反应只可能在不平衡+红叔时发生,因为爷要当做新节点,跳回1,会触发连锁反应。
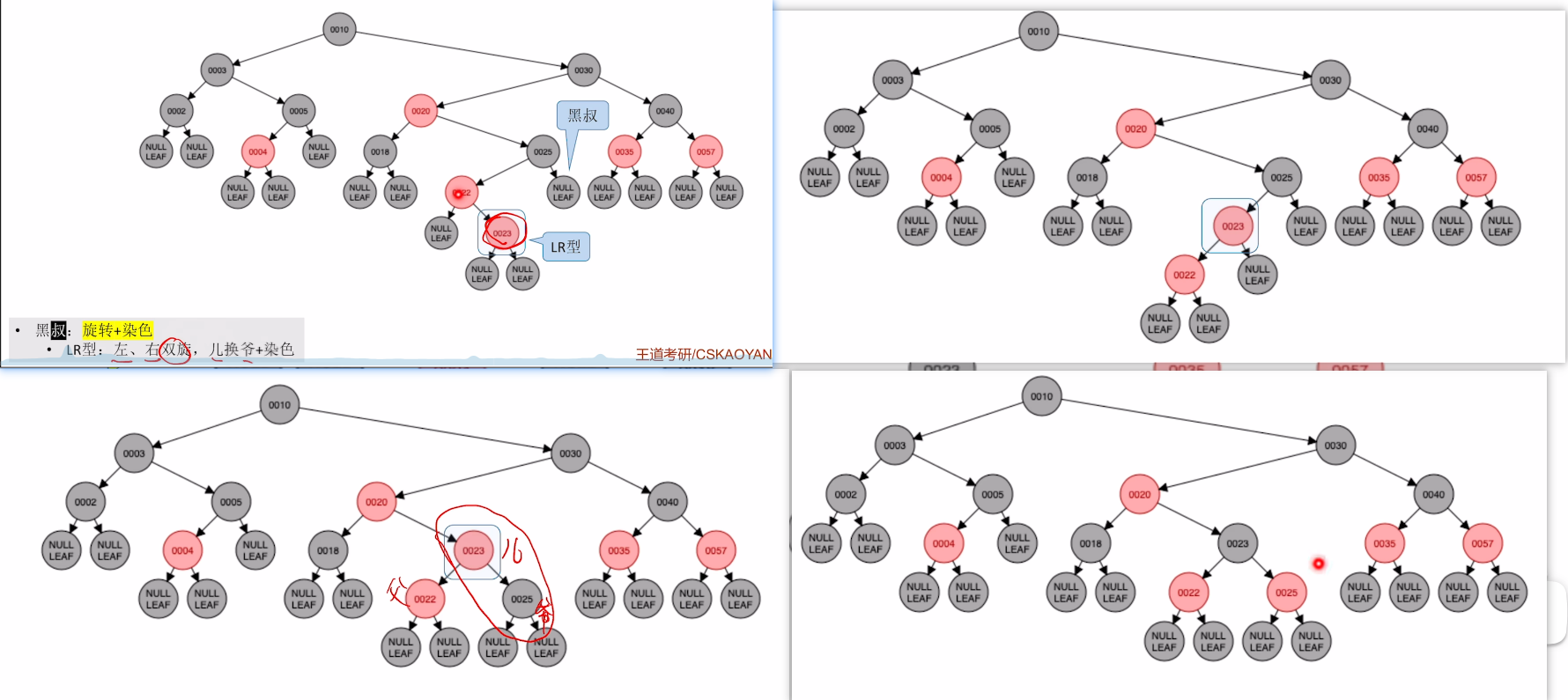
再来看一个LR的例子:不平衡+黑叔+LR=旋转+反色
- 先旋转两下
- 然后进行反色,注意只反爷儿,父不管
红黑树的删除
虽然视频没说,但是我脑子里已经有一个大致的思路了,因为删除的思路和插入其实一样。
首先按照BST删除思路,进行删除
之后必然面对结构破坏的问题,就要进行调整,我们可以利用一个逆向思维,假设自己是在进行插入操作,就当他是插入操作导致的结构破坏,然后我们用插入的思路来调整结构。
而这个思路的关键在于,你要明确儿子节点到底是哪个,又或者干脆就利用红黑树定义去修改颜色和位置
到时候凭感觉就行了,真考出来咱们就大难临头各自飞,我自己也不知道(乐)

B树
B树基础
B树插入和删除
B+树
散列查找
相关文章:

数据结构笔记——查找、排序(王道408)
文章目录 查找基本概念线性表查找顺序查找折半查找(二分)分块查找 树查找二叉排序树(BST)平衡二叉树(AVL)的插入平衡化复杂度分析 平衡二叉树的删除 红黑树红黑树的定义和性质红黑树定义红黑树性质 红黑树的…...
MySQL---搜索引擎
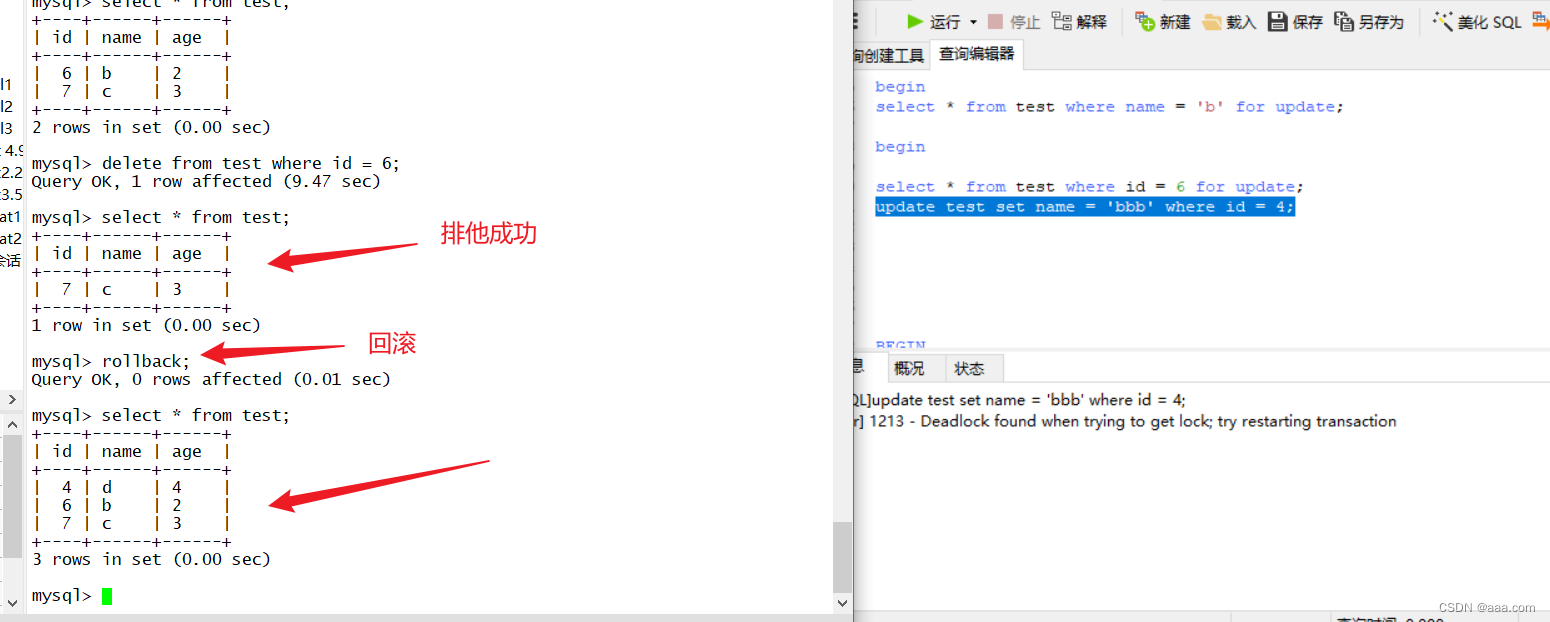
MySQL的存储引擎是什么 MySQL当中数据用各种不同的技术存储在文件中,每一种技术都使用不同的存储机制,索引技巧 锁定水平,以及最终提供的不同的功能和能力,这些就是我们说的存储引擎。 MySQL存储引擎的功能 1.MySQL将数据存储在文…...
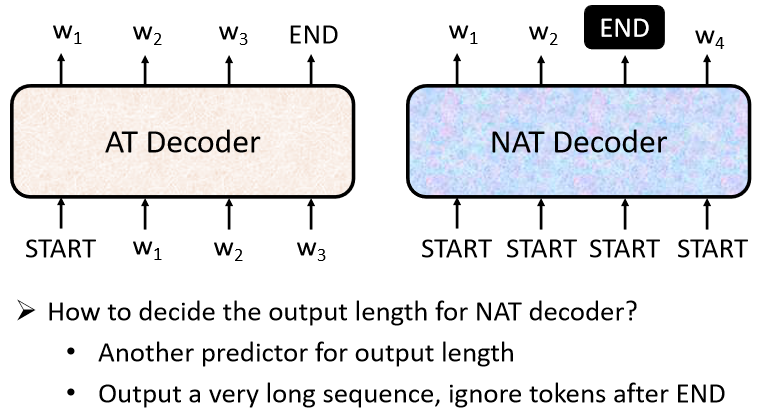
2022最新版-李宏毅机器学习深度学习课程-P32 Transformer
一、 seq2seq 1. 含义 输入一个序列,机器输出另一个序列,输出序列长度由机器决定。 文本翻译:文本至文本; 语音识别:语音至文本; 语音合成:文本至语音; 聊天机器人&#…...

如何使用商品详情API接口获取商品数据:一篇详尽的论述
一、引言 商品详情API接口是一种用于获取商品详细信息的应用程序接口。通过调用该接口,我们可以获取商品的名称、价格、描述、图片以及其他相关属性。对于电商平台、价格比较网站、数据分析等应用场景来说,商品详情API接口提供了便捷的数据获取方式。本…...

华为:手机王者归来,汽车起死回生
作为一家全球知名的科技公司,华为在通信、智能手机、平板电脑等领域拥有很高的市场份额和品牌影响力。而随着华为开始进军汽车领域,通过自主研发和合作,不断提升自己在汽车领域的竞争力,华为便也开始受到更为广泛的关注。 只不过…...

Vue3.0 provide与inject依赖注入:VCA
简介 provide 与 inject 是一种跨层级组件(祖孙)通信方式。当组件多层嵌套时,不需要将数据一层一层的向下传递,通过它俩可以实现跨层级组件通信。 provide:提供者 注入一个值,可以被后代组件接收。 prov…...

前端react入门day02-React中的事件绑定与组件
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 React中的事件绑定 React 基础事件绑定 使用事件对象参数 传递自定义参数 同时传递事件对象和自定义参…...

工业5G路由器;小体积 千兆高速通信组网
计讯物联工业路由器TR232,5G高速网络,超低时延、高可靠性,小体积、易安装、强兼容,串口/网口多设备接入联网,为用户提供高速稳定的数据传输通道 。 小体积5G工业路由器TR323,外形1047824mm࿰…...
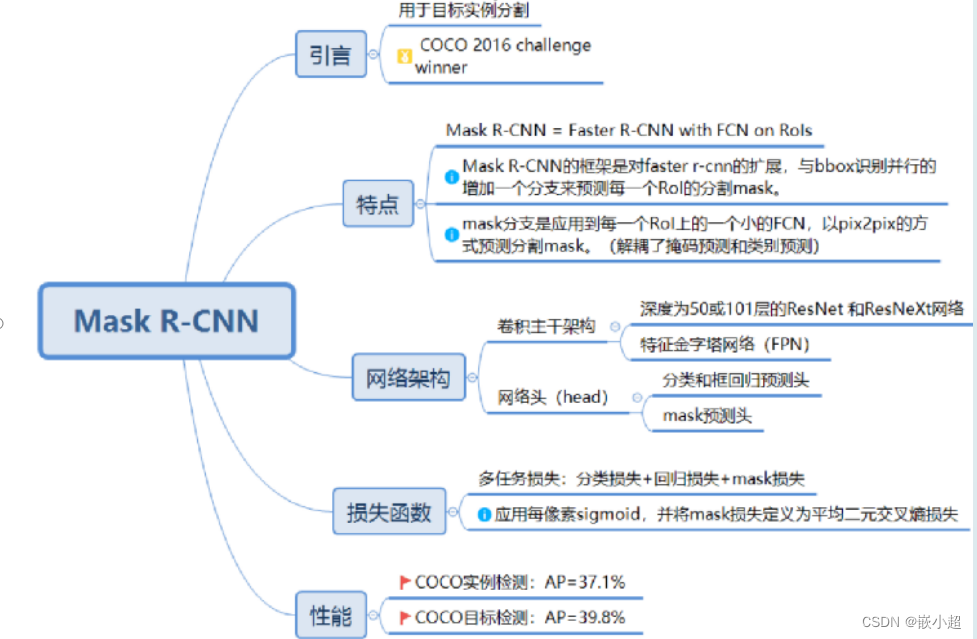
【深度学习基础】从R-CNN到Fast R-CNN,再到MaskR-CNN,发展历程讲清楚!
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
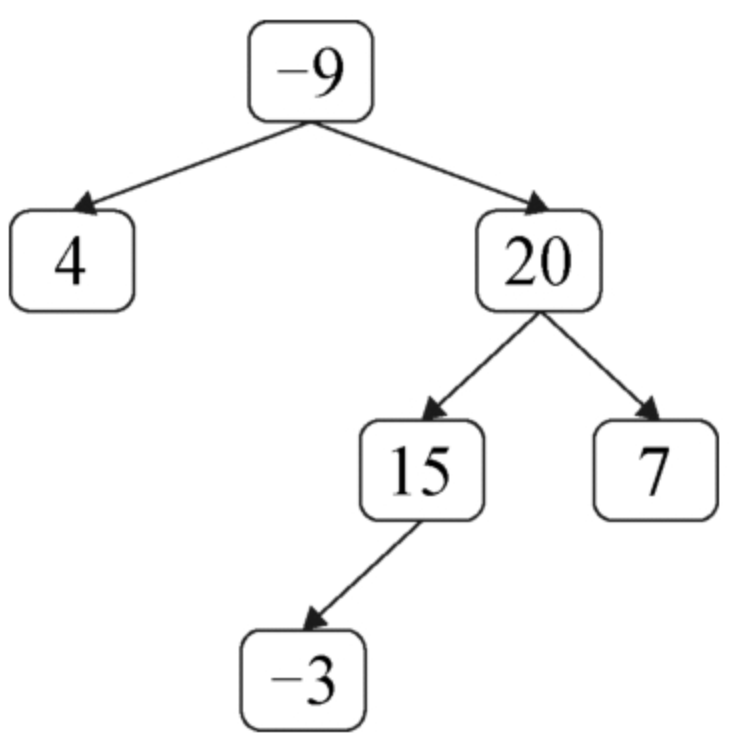
面试算法51:节点值之和最大的路径
题目 在二叉树中将路径定义为顺着节点之间的连接从任意一个节点开始到达任意一个节点所经过的所有节点。路径中至少包含一个节点,不一定经过二叉树的根节点,也不一定经过叶节点。给定非空的一棵二叉树,请求出二叉树所有路径上节点值之和的最…...

阿里云 k8s 容器服务 设置节点为不可调度的两种方法有什么区别?
两种方法的区别在于:drain 会驱逐原来节点上的所有 pod,而 cordon 只是停止调度, 禁止新的 pod 调度进来,但旧的 pod 不会受影响。...

新一代数据质量平台datavines
在我实习的第一家公司的时候,有幸参与Apache Griffin的开发,也先后在一起其他公司使用过数据质量平台,同时也调研过一些开源的数据质量平台。 最近和朋友一起参与开发了datavines数据质量平台,随着在数据行业越呆越久,…...

建议收藏《2023华为海思实习笔试-数字芯片真题+解析》(附下载)
华为海思一直以来是从业者想要进入的热门公司。但是岗位就那么多,在面试的时候,很多同学因为准备不充分,与岗位失之交臂,无缘进入该公司。今天为大家带来《2023华为海思实习笔试-数字芯片真题解析》题目来源于众多网友对笔试的记录…...

【详细教程】关于如何使用GitGitHub的基本操作汇总GitHub的密钥配置 ->(个人学习记录笔记)
文章目录 1. Git使用篇1.1 下载安装Git1.2 使用Git 2. GitHub使用篇2.1 如何git与GitHub建立联系呢?2.2 配置公钥 1. Git使用篇 1.1 下载安装Git 点击 官网链接 后,进入Git官网,下载安装包 然后根据系统类型进行下载,一般为wind…...
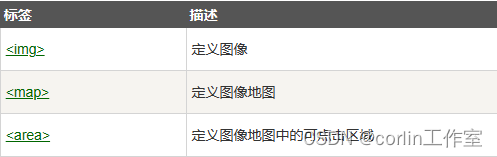
HTML样式CSS、图像
HTML样式-CSS: CSS (Cascading Style Sheets) 用于渲染HTML元素标签的样式。CSS可以通过以下方式添加到HTML中:1)、内联方式:在HTML元素中使用“style”属性;2)、内部样式表:在HTML文档头部<head>区…...

智能电表瞬时电量是什么意思?
智能电表已经成为我们进行能源管理的重要工具。其中,瞬时电量这一概念逐渐走进大众视野。那么,智能电表瞬时电量究竟是什么意思?它对我们的生活和能源管理又有哪些影响呢?下面,小编就来为大家介绍一下瞬时电量…...

Redis之 redis.config配置文件
文章目录 前言一、基本配置1.单位2.包含3.网络配置4.通用5.快照6.安全7.限制8.仅追加模式 二、总体主要介绍总结 前言 行家一出手,就知有没有,让一起学习redis.config配置文件。 一、基本配置 Redis 的配置文件位于 Redis 安装目录下,文件名…...

BIOS开发笔记 - CMOS
CMOS原来指的是一种生产电子电路的工艺,在PC上一般指的是RTC电路单元,因为早期它是由这种工艺生产出来的,所以又把RTC称作了CMOS。 RTC(Real Time Clock)即实时时钟,用于保存记录时间和日期,也可以用来做定时开机功能。RTC靠一组独立的电源给它供电,这样设计的目的就是…...

leetcode_117 填充每个节点的下一个右侧节点指针 II
文章目录 1. 题意2. 题解2.1 BFS2.2 BFS空间优化2.3 DFS序层次记录 3. Ref 1. 题意 在一颗树的同层之间用指针把他们链接起来。 填充每个节点的下一个右侧节点指针 II 2. 题解 2.1 BFS 用一个变量记录下同层最右侧的节点,当遍历到时更新下一层的最右侧节点即可…...
亲测 IDEA Pycharm 全家桶 自动重置免费30天
理论上是通用的 插件市场安装 添加第三方插件仓库地址 在Settings/Preferences... -> Plugins 内手动添加第三方插件仓库地址:https://plugins.zhile.io 搜索:IDE Eval Reset插件进行安装。如果搜索不到请注意是否做好了上一步?网络是否…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
