C++变参模板的使用
C17
1. 使用编译器if常量表达式
template<typename T, typename U, typename... Ts>
void syszuxPrint(T arg1, Ts... arg_left)
{std::cout << arg1 << ", ";if constexpr (sizeof...(arg_left) > 0){syszuxPrint(arg_left...);}
}但是这种方式对于我个人遇到的问题有点不适用,我需要的是第一是数据指针,然后第二个参数、第三个参数是数据的宽高,然后后面才是变参,这样递归处理的话不行
2. C17折叠表达式
template<typename... Ts>
void syszuxPrint(Ts... arg_left){(std::cout<< ... << arg_left) << std::endl;
}int main(int argc, char** argv)
{syszuxPrint(719,7030,"civilnet");
}上述折叠表达式存在同样的问题
3. 变种折叠表达式
template <typename First, typename... Args>
void syszuxPrint(First first, int iWidth, int iHeight, Args... args)
{std::cout << first << std::endl;std::cout << iWidth << std::endl;std::cout << iHeight << std::endl;auto printWhiteSpace = [](const auto& arg) { std::cout << " " << arg << std::endl;};(..., printWhiteSpace(args)); // op是,
}这样可以
相关文章:

C++变参模板的使用
C17 1. 使用编译器if常量表达式 template<typename T, typename U, typename... Ts> void syszuxPrint(T arg1, Ts... arg_left) {std::cout << arg1 << ", ";if constexpr (sizeof...(arg_left) > 0){syszuxPrint(arg_left...);} } 但是这…...
get和post类似)
【二、http】go的http基本请求设置(设置查询参数、定制请求头)get和post类似
一、设置url后边的参数,(get和post请求为例子) func requstByParamsGet(){requst, err : http.NewRequest(http.MethodGet, "http://httpbin.org/get", nil)if err ! nil {fmt.Println("ss")}params : make(url.Values)p…...
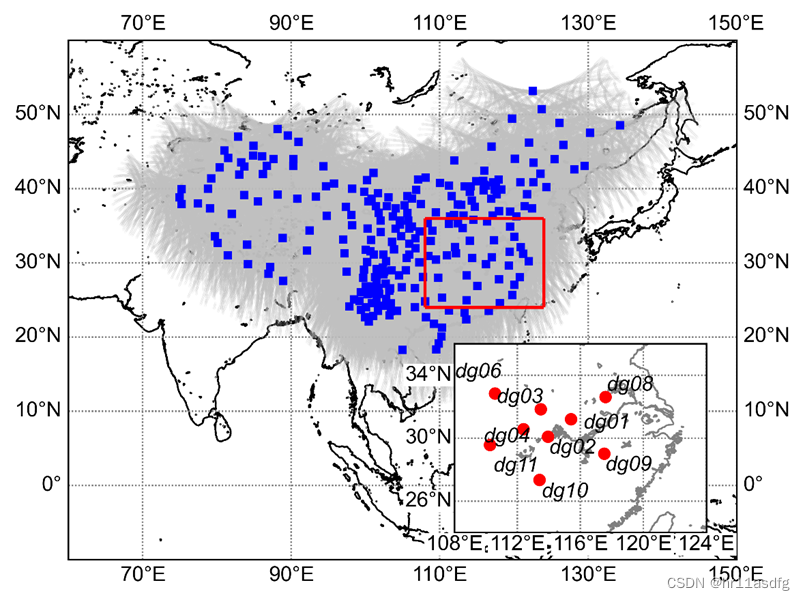
[学习笔记]python绘制图中图(绘制站点分布图)
背景 在绘制站点分布图时,有时需要采用图中图的方式,以便于在一张图中尽可能多的表达信息。此处记录一下利用python matplotlib绘制图中图的脚本,方便然后查询。 包含数据 该绘图脚本中包含以下数据: CMONOC站点分布ÿ…...

回归预测 | Matlab实现POA-CNN-SVM鹈鹕算法优化卷积神经网络-支持向量机多变量回归预测
Matlab实现POA-CNN-SVM鹈鹕算法优化卷积神经网络-支持向量机多变量回归预测 目录 Matlab实现POA-CNN-SVM鹈鹕算法优化卷积神经网络-支持向量机多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.POA-CNN-SVM鹈鹕算法优化卷积神经网络-支持向量机的多变量回归…...

React 学习笔记
React React.js是一个开源的JavaScript库,由Facebook于2013年开发,用于构建用户界面或UI组件。它主要用于构建单页应用程序或SPA,并且可以在Web和移动应用程序中使用。React.js使用虚拟DOM来提高性能,并使用组件化的方式来实现代…...
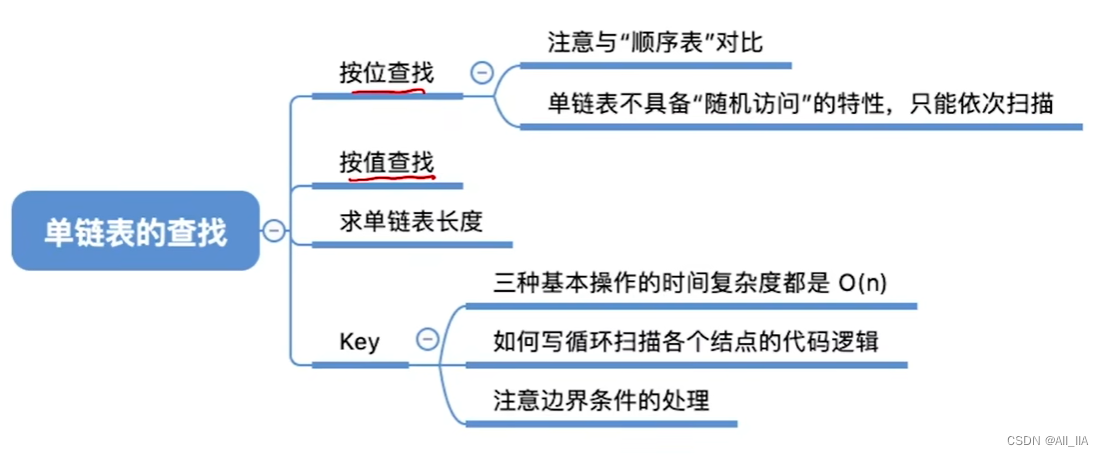
单链表的查找(按值查找、按位查找)(数据结构与算法)
什么是单链表? 单链表是一种常见的链式数据结构,用于存储和操作数据元素的集合。它由一系列的节点组成,每个节点包含两个部分:数据域和指针域。 单链表的每个节点包含了存储数据的数据域,以及指向下一个节点的指针域。…...

Qt 6.6 发布
@TOC 前言 Qt 6.6 发布于2023年10月10日 https://www.qt.io/blog/qt-6.6-releasedQt 6.6 系列源码下载 https://download.qt.io/official_releases/qt/6.6/Qt 在线安装器下载 https://download.qt.io/official_releases/online_installers/国内镜像下载 在线安装器(维护工具)…...

unity工程
1首先我们来熟悉一下Unity每个文件夹的作用 1.assets:工程资源文件夹 2.library:库文件夹 3.logs:日志文件夹 4.obj:编译产生中间文件 5.packages:包配置信息 6:projectsettings:工程设置…...
)
蓝桥杯官网练习题(地址转换)
题目描述 Excel 是最常用的办公软件。每个单元格都有唯一的地址表示。比如:第 12 行第 4 列表示为:"D12",第 5 行第 255 列表示为"IU5"。 事实上,Excel 提供了两种地址表示方法,还有一种表示法叫…...

力扣labuladong——一刷day19
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣303. 区域和检索 - 数组不可变二、力扣304. 二维区域和检索 - 矩阵不可变 前言 巧用前缀和 前缀和技巧适用于快速、频繁地计算一个索引区间内的元素之…...
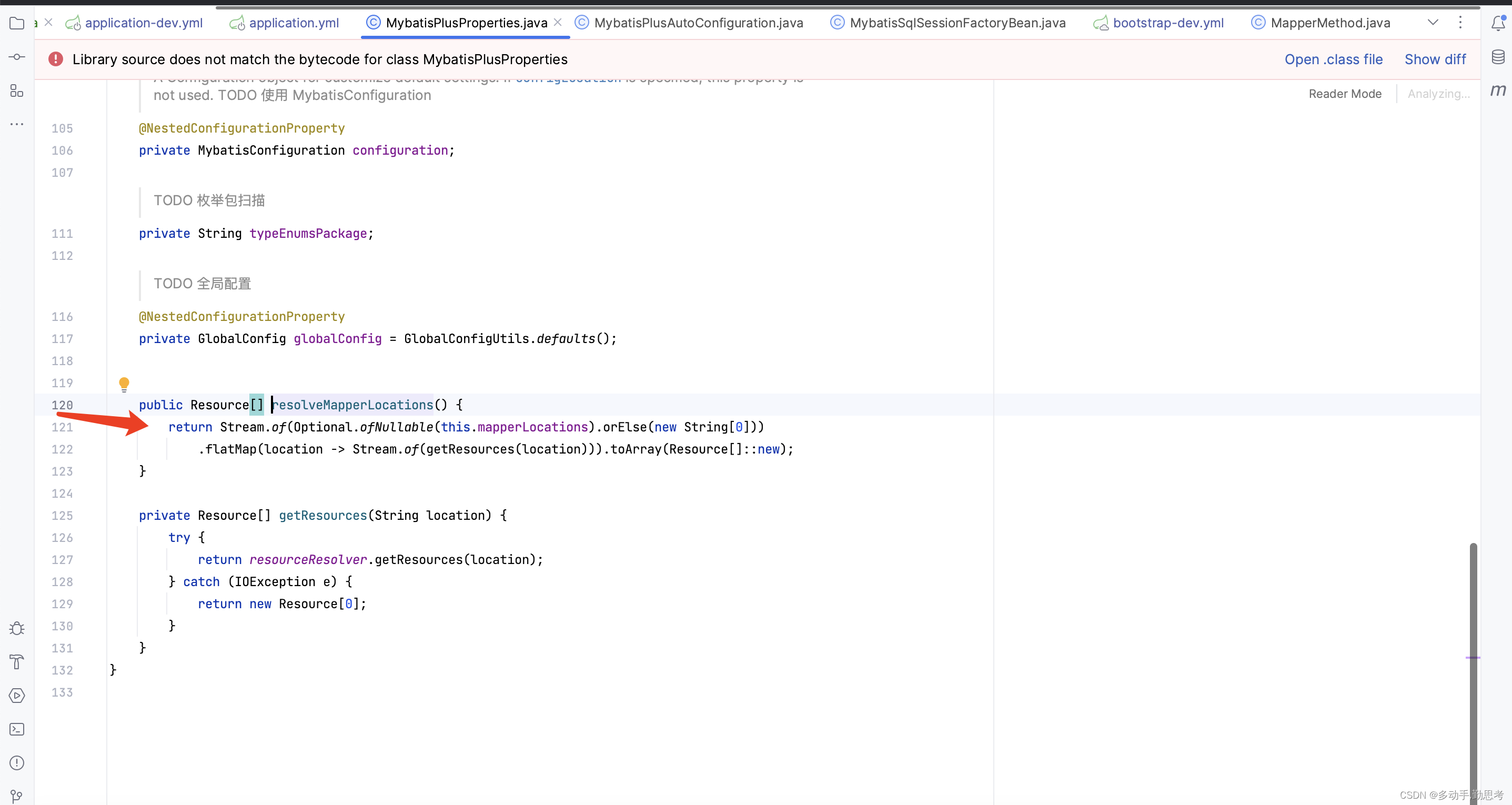
MyBatis无法读取XML中的Method的乌龙事件
事件背景 同事反馈,相同的jar包,在多人本地的电脑、多台服务器中,都是可以正常启动的,只有在其中一台服务器,简称它为A,无法启动,因为启动后的初始化操作中有一个调用mybatis方法的操作&#x…...

LeetCode----76. 最小覆盖子串
题目 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。 注意: 对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。 如果 s 中存在这样的子串,我们保…...

app逆向入门之车智赢
声明:本文仅限学习交流使用,禁止用于非法用途、商业活动等。否则后果自负。如有侵权,请告知删除,谢谢!本教程也没有专门针对某个网站而编写,单纯的技术研究 目录 案例分析技术依赖参数分析效果展示代码分享…...

LeetCode——数组 移除元素(Java)
移除元素 简介[简单] 27. 移除元素[简单] 26. 删除有序数组中的重复项[简单] 283. 移动零[简单] 844. 比较含退格的字符串[简单] 977. 有序数组的平方 简介 记录一下自己刷题的历程以及代码。写题过程中参考了 代码随想录。会附上一些个人的思路,如果有错误&#x…...

enum和Collection.stream()你这样用过么
最近在做一个数据图表展示的功能,显示订单近七天或者近半月的数量和金额。可以理解成下图所示的样子: 我是用枚举和集合的stream方法实现的数据初始化和组装,枚举用来动态初始化时间范围,集合的stream方法来将初始化的数据转换成…...
unittest与pytest的区别
Unittest vs Pytest 主要从用例编写规则、用例的前置和后置、参数化、断言、用例执行、失败重运行和报告这几个方面比较unittest和pytest的区别: 用例编写规则 用例前置与后置条件 断言 测试报告 失败重跑机制 参数化 用例分类执行 如果不好看,可以看下面表格&…...

YOLOv7优化策略:IOU系列篇 | 引入MPDIoU,WIoU,SIoU,EIoU,α-IoU等创新
💡💡💡本文独家改进:MPDIoU,WIoU,SIoU,EIoU,α-IoU等二次创新,总有一种适合你的数据集 MPDIoU,WIoU,SIoU,EIoU,α-IoU | 亲测在多个数据集能够实现大幅涨点 收录: YOLOv7高阶自研专栏介绍: http://t.csdnimg.cn/tYI0c ✨✨✨前沿最新计算机顶会复现 …...
SQL Server2000mdf升级SQL Server2005数据库还原
SQL Server2000数据库还原sqlserver 2000mdf升级 sqlserver 2008数据库还原SQL Server2005数据库脚本 sqlserver数据库低版本升级成高版本 sqlserver数据库版本升级 数据库版本还原 如果本机安装了sqlserver2012或者sqlserver2019等高版本 怎么样才能运行sqlserver2000的数据库…...

webSocket推送太快导致前端渲染卡顿问题优化
优化思路: 把webSocket接收到的数据用一个数组存起来,达到一定长度再统一渲染,可根据推送数据的速度适当调解数组长度限制,如果一段时间内改数组长度打不要渲染条件,就用定时器之间渲染 data() {return {tempDataWsLi…...
泛型总结)
(Java)泛型总结
泛型类 public class Student<E> {private E a;public Student(E a){this.aa;}public void show(){System.out.println(a);} } 泛型方法 public <E> void show(E a){System.out.println(a);} 泛型接口 public interface Inter <T>{void show(T a); } 类…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
