DAY43 完全背包理论基础 + 518.零钱兑换II
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
假设背包最大重量为4。物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
每件商品都有无限个。
因此在01背包中,我们为了使每件物品只被加入背包一次,在内层遍历的时候我们选择了倒序遍历。但是在完全背包中,物品的数量是无限的,因此可以被添加多次,所以要从小到大去遍历。
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}其实还有一个很重要的问题,为什么遍历物品在外层循环,遍历背包容量在内层循环?
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!
因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
遍历物品在外层循环,遍历背包容量在内层循环,状态如图:
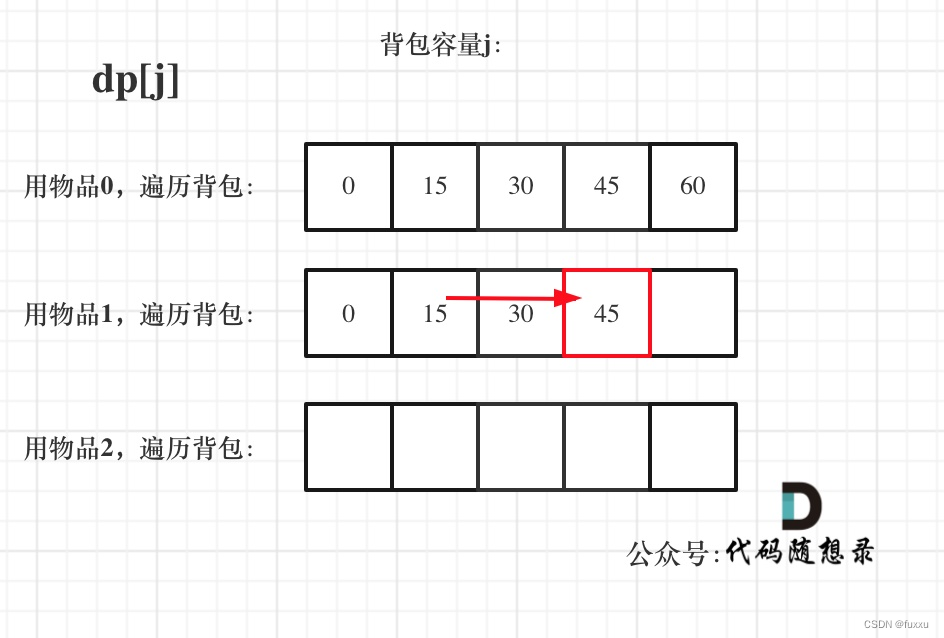
遍历背包容量在外层循环,遍历物品在内层循环,状态如图:
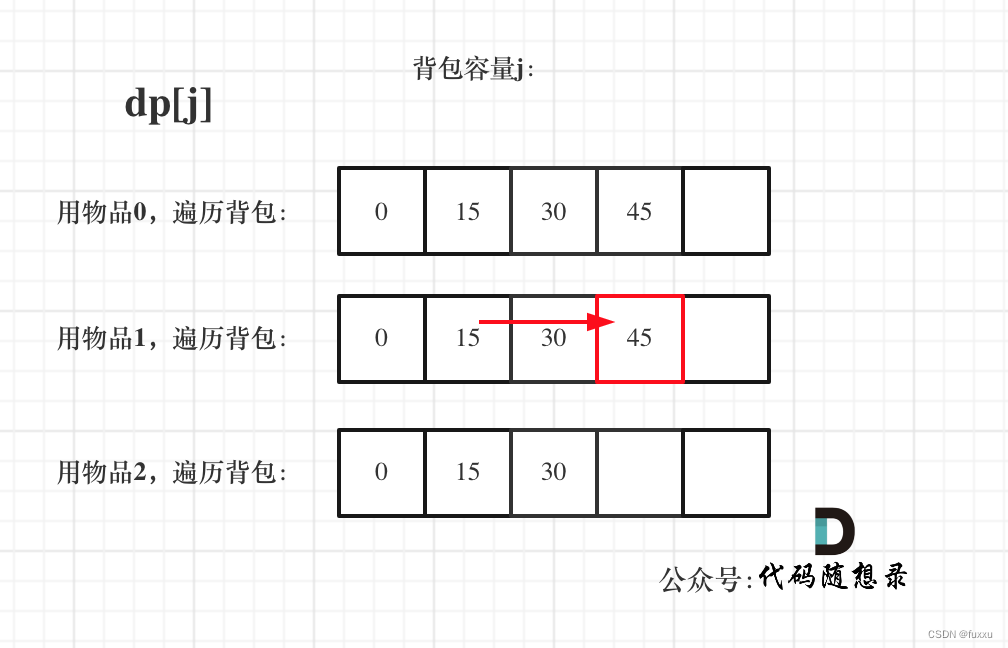
看了这两个图,大家就会理解,完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值(这个值就是下标j之前所对应的dp[j])。
518. 零钱兑换II
题目要求:给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
- 输入: amount = 5, coins = [1, 2, 5]
- 输出: 4
解释: 有四种方式可以凑成总金额:
- 5=5
- 5=2+2+1
- 5=2+1+1+1
- 5=1+1+1+1+1
思路
完全背包问题,容量就是amount,物品是coins。dp[i]表示组成i大小背包容量的方式数量。同时题目中强调凑成总金额的是组合,所以不强调元素之间的顺序。
状态转移方程就是:dp[i] += dp[j-coins[i]],与昨天遇到的题目相同。
这个递推公式大家应该不陌生了,我在讲解01背包题目的时候在这篇494. 目标和 (opens new window)中就讲解了,求装满背包有几种方法,公式都是:dp[j] += dp[j - nums[i]];
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount+1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); ++i) {for (int j = coins[i]; j <= amount; ++j) {dp[j] += dp[j - coins[i]];}}return dp[amount];}
};377. 组合总和 Ⅳ
题目要求:给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
- nums = [1, 2, 3]
- target = 4
所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
思路
与上一个题目类似,但是本题是排序,强调序列的顺序。而上一个题目是组合,不强调顺序。
- 确定遍历顺序
个数可以不限使用,说明这是一个完全背包。
得到的集合是排列,说明需要考虑元素之间的顺序。
本题要求的是排列,那么这个for循环嵌套的顺序可以有说法了。、
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target+1, 0);dp[0] = 1;for (int i = 0; i <= target; ++i) { // 遍历背包for (int j = 0; j < nums.size(); ++j) { // 遍历物品if (i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
};- 时间复杂度: O(target * n),其中 n 为 nums 的长度
- 空间复杂度: O(target)
C++测试用例有两个数相加超过int的数据,所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
- Day43总结
- 背包问题的遍历顺序是一门学问,01背包物品只能用一次外层是物品内层倒叙是容量;
- 完全背包的组合问题不强调顺序,物品可以用无限次,外层是物品,内层是背包容积的正序;
- 完全背包的排列问题,强调顺序,外层是背包容积,内层是物品,这样大编号的物品也可以出现在前面。
相关文章:

DAY43 完全背包理论基础 + 518.零钱兑换II
完全背包 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。 完全背包和01背包问题唯一不同…...
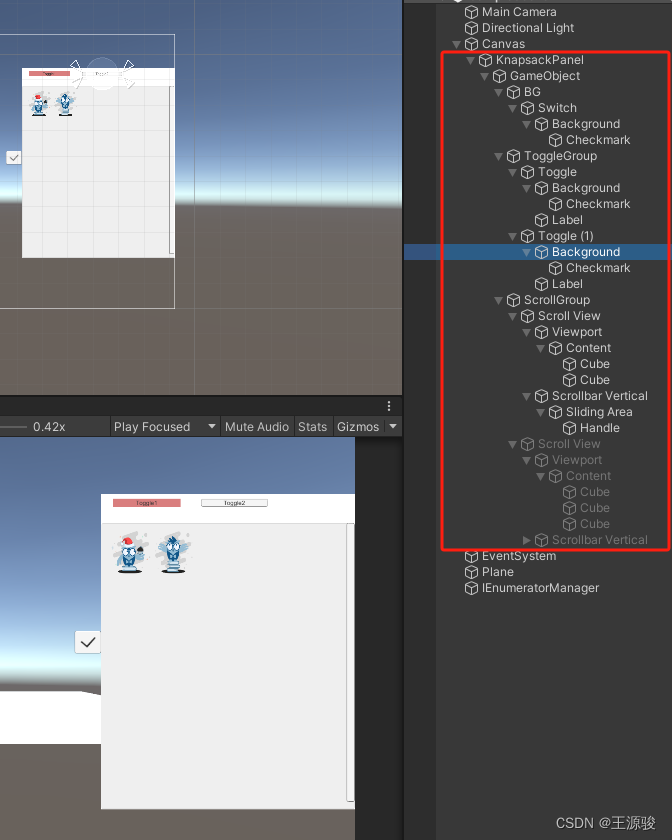
unity 从UI上拖出3D物体,(2D转3D)
效果展示: 2D转3D视频 UI结构 UI组件挂载 UI结构 这个脚本挂载到 3D物体身上 using DG.Tweening; using System.Collections; using System.Collections.Generic; using UnityEngine;public class DragGame : MonoBehaviour {[HideInInspector]public bool isDrag…...

win10pycharm和anaconda安装和环境配置教程
windows10 64位操作系统下系统运行环境安装配置说明 下载和安装Anaconda,链接https://www.anaconda.com/download 下载完后,双击exe文件 将anaconda自动弹出的窗口全部关掉即可,然后配置高级系统变量 根据自己的路径,配置…...

[C++ 中]:6.类和对象下(static成员 + explicit +友元函数 + 内部类 + 编译器优化)
(static成员 explicit 友元函数 内部类 编译器优化) 一.static 成员:1.概念引入:1-1:定义全局变量记录个数? 2.如果有多个类需要分开去记录类对象的个数?2-1:可不可以声明成员变量解决&#…...

ONES Design UI 组件库环境搭建
这个 ONES Design UI 组件库 是基于 Ant Design 的 React UI 组件库,主要用于企业级研发管理工具的研发。 首先用 React 的脚手架搭建一个项目: npx create-react-app my-app cd my-app目前 ONES Design UI 组件库 托管在 ONES 私有的 npm 仓库上, 因此…...

支付宝AI布局: 新产品助力小程序智能化,未来持续投入加速创新
支付宝是全球领先的独立第三方支付平台,致力于为广大用户提供安全快速的电子支付/网上支付/安全支付/手机支付体验,及转账收款/水电煤缴费/信用卡还款/AA收款等生活服务应用。 支付宝不仅是一个支付工具,也是一个数字生活平台,通过…...
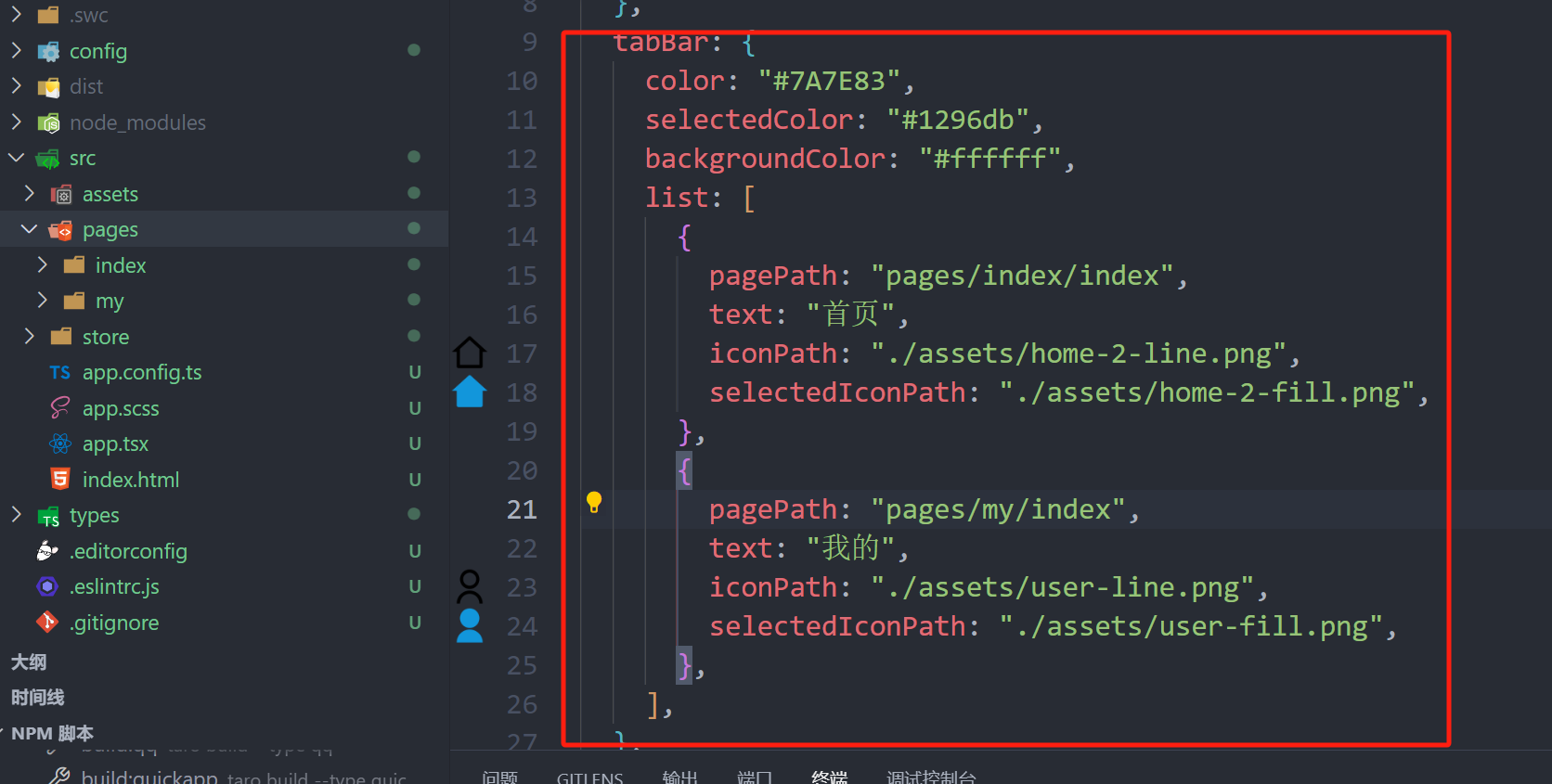
taro全局配置页面路由和tabBar页面跳转
有能力可以看官方文档:Taro 文档 页面路由配置,配置在app.config.ts里面的pages里: window用于设置小程序的状态栏、导航条、标题、窗口背景色,其配置项如下: tabBar配置:如果小程序是一个多 tab 应用&…...

【k8s】pod进阶
一、资源限制 1、资源限制的概念 当定义 Pod 时可以选择性地为每个容器设定所需要的资源数量。 最常见的可设定资源是 CPU 和内存大小,以及其他类型的资源。 当为 Pod 中的容器指定了 request 资源时,调度器就使用该信息来决定将 Pod 调度到哪个节点上…...
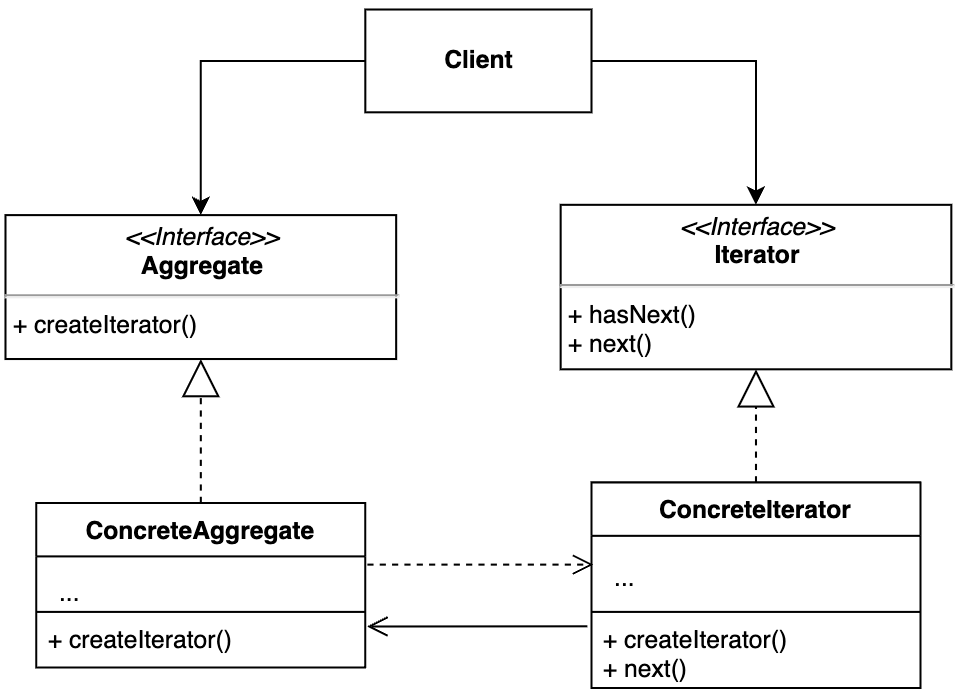
【设计模式】第18节:行为型模式之“迭代器模式”
一、简介 迭代器模式(Iterator Design Pattern),也叫作游标模式(Cursor Design Pattern)。 在通过迭代器来遍历集合元素的同时,增加或者删除集合中的元素,有可能会导致某个元素被重复遍历或遍…...

【数据结构】单链表OJ题
前言: 本节博客将讲解单链表的反转,合并有序链表,寻找中间节点及约瑟夫问题 文章目录 一、反转链表二、合并有序链表三、链表的中间结点四、环形链表的约瑟夫问题 一、反转链表 要反转链表,我们需要遍历链表并改变每个节点的 next 指针&#…...

智能工厂架构
引:https://www.bilibili.com/video/BV1Vs4y167Kx/?spm_id_from=333.788&vd_source=297c866c71fa77b161812ad631ea2c25 智能工厂框架 智能工厂五层系统框架 MES 数据共享 <...

阿里云多款ECS产品全面升级 性能最多提升40%
“阿里云始终围绕‘稳定、安全、性能、成本、弹性’的目标不断创新,为客户创造业务价值。”10月31日,杭州云栖大会上,阿里云弹性计算计算产品线负责人张献涛表示,通过持续的产品和技术创新,阿里云发布了HPC优化实例等多…...
)
责任链模式(Chain of Responsibility)
责任链模式是对象的行为模式。使多个对象都有机会处理请求,从而避免请求的发送者和接受者直接的耦合关系。 public abstract class Handler {protected Handler successor;public abstract void handlerRequest(String condition);protected Handler getSuccessor()…...
文件管理技巧:根据大小智能分类并移动至目标文件夹
在文件管理过程中,我们经常需要整理大量的文件。根据文件的大小,将其智能分类并移动至目标文件夹,可以帮助我们更高效地管理文件,提高工作效率。通过使用云炫文件管理器可以根据文件大小进行智能分类和移动至目标文件夹࿰…...

具有自主产权的SaaS门店收银系统全套源码输出
PHPMysql前后端分离, 小程序线上商城; 进销存管理库存盘点, 多仓库库存调拨, 会员系统。 消费者扫码查价系统。...
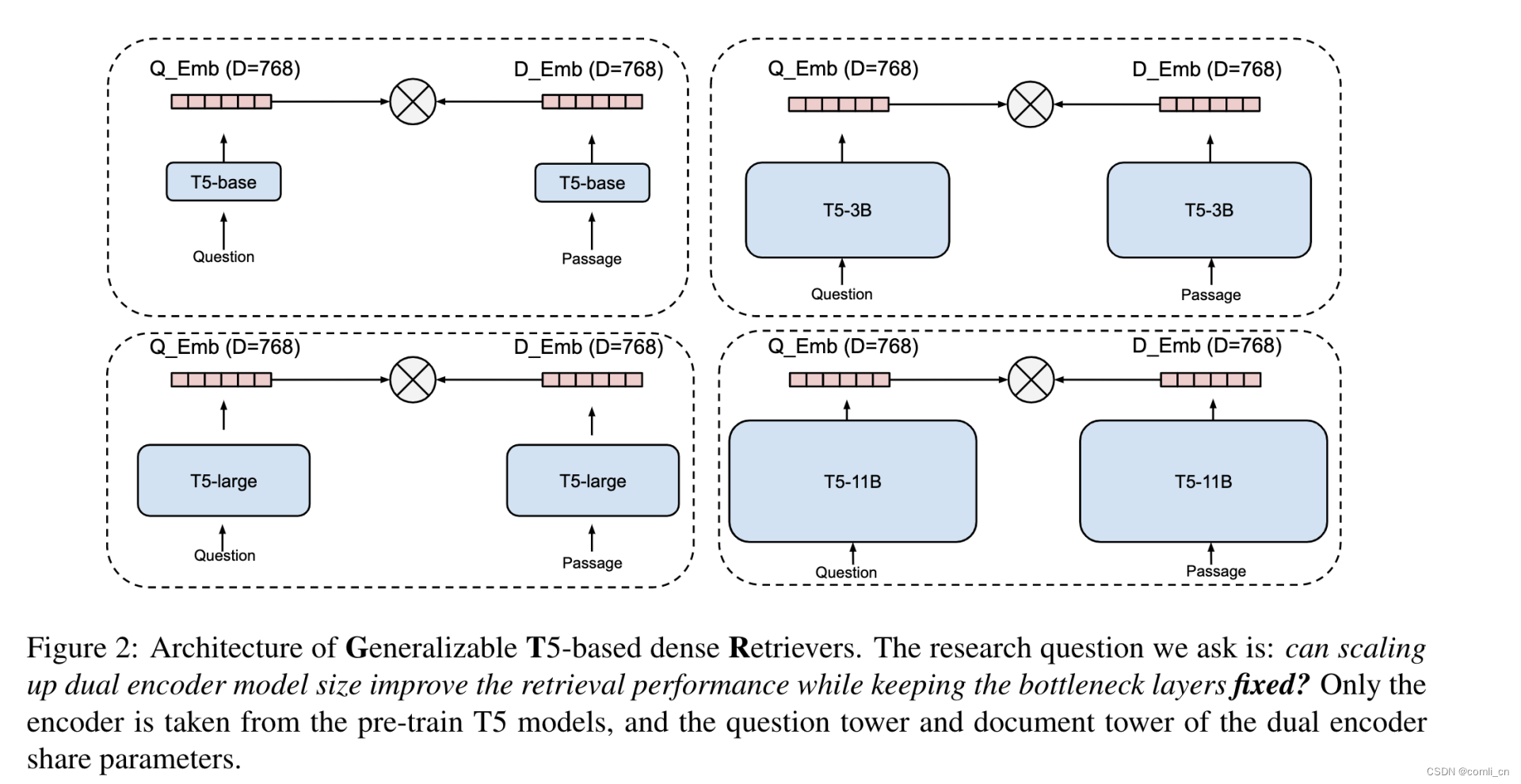
论文阅读:One Embedder, Any Task: Instruction-Finetuned Text Embeddings
1. 优势 现存的emmbedding应用在新的task或者domain上时表现会有明显下降,甚至在相同task的不同domian上的效果也不行。这篇文章的重点就是提升embedding在不同任务和领域上的效果,特点是不需要用特定领域的数据进行finetune而是使用instuction finetun…...

[BUUCTF NewStarCTF 2023 公开赛道] week3 crypto/pwn
居然把第3周忘了写笔记了. 后边难度上来了,还是很有意思的 Crypto Rabins RSA rsa一般要求e与phi互质,但rabin一般用2,都是板子题也没什么好解释的 from Crypto.Util.number import * from secret import flag p getPrime(64) q getPrime(64) assert p % 4 3 assert q %…...
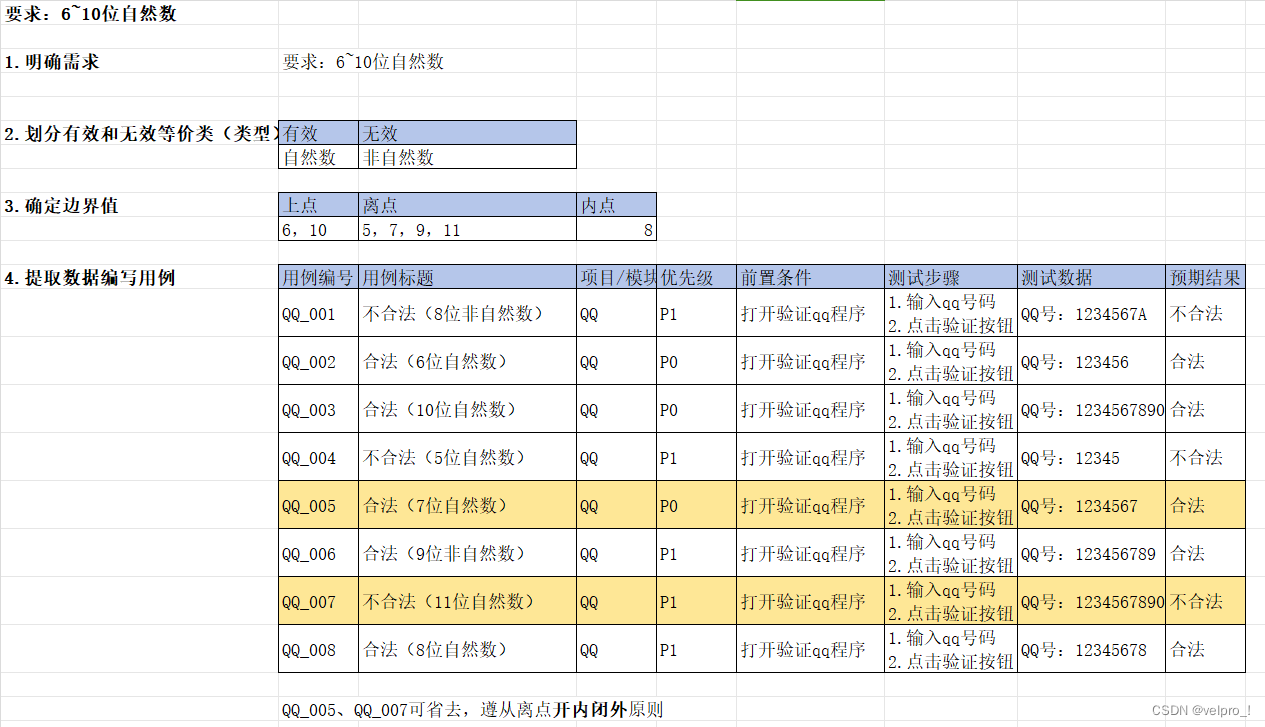
软件测试---边界值分析(功能测试)
能对限定边界规则设计测试点---边界值分析 选取正好等于、刚好大于、刚好小于边界的值作为测试数据 上点: 边界上的点 (正好等于);必选(不考虑区开闭) 内点: 范围内的点 (区间范围内的数据);必选(建议选择中间范围) 离点: 距离上点最近的点 (刚好…...
使用pytorch处理自己的数据集
目录 1 返回本地文件中的数据集 2 根据当前已有的数据集创建每一个样本数据对应的标签 3 tensorboard的使用 4 transforms处理数据 tranfroms.Totensor的使用 transforms.Normalize的使用 transforms.Resize的使用 transforms.Compose使用 5 dataset_transforms使用 1 返回本地…...

http进一步认识
好久不见各位,今天为大家带来http协议的进一步认识 文章目录 👀http协议的认识👀新的改变 👀http协议的认识 http协议经历了三个版本的演化,HTTP0.9是第一个版本的协议,它的组成极其简单,只涉…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
