CSP-J 2023真题解析
T1 小苹果
一、题目链接
P9748 [CSP-J 2023] 小苹果
二、题目大意
现有 n n n 个苹果从左到右排成一列,编号为从 1 1 1 到 n n n。
每天都会从中拿走一些苹果。拿取规则是,从左侧第 1 1 1 个苹果开始、每隔 2 2 2 个苹果拿走 1 1 1 个苹果。随后将剩下的苹果按原先的顺序重新排成一列。
现求多少天能拿完所有的苹果,而编号为 n n n 的苹果是在第几天被拿走的
数据范围: 1 ≤ n ≤ 1 0 9 1\leq n\leq10^9 1≤n≤109
三、题目分析
- 根据题目意思很容易想到时间复杂度为 O ( n ) O(n) O(n) 的暴力模拟方法,这样就已经足够拿到 90 90 90 分了
- 因为满分的要求是 1 0 9 10^9 109,所以这大概是需要 log \log log 级的时间复杂度
- 仔细观察之后,你能发现每次会大约拿走 1 3 \frac{1}{3} 31 的苹果,所以最终拿的次数是 O ( log n ) O(\log n) O(logn) 级别的,所以只要我们能按轮次处理计科得到满分
- 每一轮具体拿走的苹果数量是 ⌈ n 3 ⌉ \lceil\frac{n}{3}\rceil ⌈3n⌉,因为是从第一个开始拿的
- 注意,每一轮之后 n n n 都会更新
- 不难发现最后一个苹果只会在 n m o d 3 = 1 n\mod 3=1 nmod3=1 时被取走,所以再判断一下即可。
- 时间复杂度 O ( log n ) O(\log n) O(logn)
四、正解程序
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstdlib>using namespace std;
typedef long long ll;
int main()
{ll n;scanf("%lld",&n);ll t=n,ans1=0,ans2=0;while(t){ll x=(t+2)/3;ans1++;if(ans2==0 && t%3==1)ans2=ans1;t-=x;}printf("%lld %lld\n",ans1,ans2);return 0;
}
T2 公路
一、题目链接
P9749 [CSP-J 2023] 公路
二、题目大意
现有一条公路上一共有 n n n 个站点,编号为从 1 1 1 到 n n n。其中站点 i i i 与站点 i + 1 i+1 i+1 的距离为 v i v_i vi 公里。每个站点都可以加油,编号为 i i i 的站点一升油的价格为 a i a_i ai 元,且每个站点只出售整数升的油。
现要从站点 1 1 1 开车到站点 n n n,一开始油箱为空。油箱可以装下任意多的油,且每升油可以让车前进 d d d 公里。问至少要花多少钱加油
数据范围: 1 ≤ n ≤ 1 0 5 , 1 ≤ d ≤ 1 0 5 , 1 ≤ v i ≤ 1 0 5 , 1 ≤ a i ≤ 1 0 5 1\leq n\leq 10^5,1\leq d\leq 10^5,1\leq v_i\leq10^5,1\leq a_i\leq10^5 1≤n≤105,1≤d≤105,1≤vi≤105,1≤ai≤105
三、题目分析
- 为了消费最小,所以我们一定要尽可能加便宜的油,毕竟油箱无限大
- 所以很显然我们可以有一个贪心的思路,选择一个递减的油价序列进行加油,即加油跑到下一个比当前的油更便宜的地方(尽可能刚好把油耗光)再加油
- 这样当然可以实现,但稍微有一点点复杂,我们可以做一点等价
- 我们到一个加油站的时先不加油,等到缺油的时候再从之前经过的最便宜的加油站虚空加油。如果出现更便宜的加油站,我们就更新即可。以上两个思路显然是等价的。
- 时间复杂度 O ( n ) O(n) O(n)
四、正解程序
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdlib>using namespace std;
typedef long long ll;
const ll maxn=100010;
ll n,d,v[maxn],a[maxn];
int main()
{scanf("%lld%lld",&n,&d);for(ll i=1;i<=n-1;i++)scanf("%lld",&v[i]);for(ll i=1;i<=n;i++)scanf("%lld",&a[i]);ll price=a[1],rest=0,ans=0;for(ll i=1;i<=n-1;i++){price=min(a[i],price);if(rest>=v[i]){rest-=v[i];continue;}ll temp=(v[i]-rest+d-1)/d;ans+=temp*price;rest=temp*d+rest-v[i];}printf("%lld\n",ans);return 0;
}
T3 一元二次方程
一、题目链接
P9750 [CSP-J 2023] 一元二次方程
二、题目大意
如题所示,一个字都别漏,纯纯的模拟题
三、题目分析
-
读完题之后不难发现这就是纯纯的模拟,跟着做就完了
-
做模拟题最关键的问题是,很多时候你不知道它在说什么,你大概率美学过,没看过。但这不重要,你只需要读完全部题目即可,它一定会给足所有信息,只需认真读题。
-
毕竟有时候还有大学知识,而好多参赛者都是小学生。要有耐心和信心。
-
实在理解不了求根公式的话,可以针对题目给你的特殊性质 C C C 来骗分,代入所有 [ − 2000 , 2000 ] [−2000,2000] [−2000,2000] 的整数来判断是否有解,以及求最大的解,这样可以得到 50 50 50 分
-
你还需要枚举 Δ \Delta Δ 的平方因子来开方,使得 Δ \sqrt{\Delta} Δ 变得最简,这需要 O ( m ) O(m) O(m) 的思想。
-
但是模拟题的问题在于,你很难拿到满分,你有一下问题需要注意
-
如果出现 1 \sqrt{1} 1,请让它变成 1 1 1
-
如果出现乘法和除法的 1 1 1 请将它省略
-
a a a 可能是负数,所以较大的解不一定是 − b + Δ 2 a \frac{-b+\sqrt{\Delta}}{2a} 2a−b+Δ,而是 − b − Δ 2 a \frac{-b-\sqrt{\Delta}}{2a} 2a−b−Δ
-
根据题目意思,你应该保证分母为正
-
-
时间复杂度 O ( T m ) O(Tm) O(Tm)
四、正解程序
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdlib>using namespace std;
typedef long long ll;
ll T,m;
ll gcd(ll a,ll b)
{if(a%b==0)return b;return gcd(b,a%b);
}
int main()
{scanf("%lld%lld",&T,&m);while(T--){ll a,b,c;scanf("%lld%lld%lld",&a,&b,&c);ll det=b*b-4*a*c;if(det<0){printf("NO\n");continue;}ll q1=-b,q2=1,q3=2*a;for(ll i=2;i*i<=det;i++)while(det%(i*i)==0)q2*=i,det/=i*i;if(q3<0)q3=-q3,q1=-q1;if(det==1)det=0,q1+=q2;ll gcd1=gcd(abs(q1),q3);ll gcd2=gcd(q2,q3);if(det==0){if(q1%q3==0)printf("%lld",q1/q3);elseprintf("%lld/%lld",q1/gcd1,q3/gcd1);}else{if(q1!=0){if(q1%q3==0)printf("%lld",q1/q3);elseprintf("%lld/%lld",q1/gcd1,q3/gcd1);printf("+");}if(q2/gcd2!=1)printf("%lld*",q2/gcd2);printf("sqrt(%lld)",det);if(q3/gcd2!=1)printf("/%lld",q3/gcd2);}printf("\n");}return 0;
}
T4 旅游巴士
一、题目链接
P9751 [CSP-J 2023] 旅游巴士
二、题目大意
有一张图,图上有 n n n 个点, m m m 条边。 1 1 1 号点为起点, n n n 号点为终点。每个点有一个时刻 a i a_i ai,要求不能早于这个时刻通过此点,且不允许在同种任何地方停留。
现要从起点一直走到终点,要求到达终点的时刻一定是 k k k 的非负整数倍。问最早到终点的时刻是多少,如果不存在这样的方案,输出 − 1 -1 −1。
数据范围: 2 ≤ n ≤ 1 0 4 , 1 ≤ m ≤ 2 × 1 0 4 , 1 ≤ k ≤ 100 , 1 ≤ u i , v i ≤ n , 0 ≤ a i ≤ 1 0 6 2\leq n\leq10^4,1\leq m\leq2\times10^4,1\leq k\leq100,1\leq u_i,v_i\leq n,0\leq a_i\leq10^6 2≤n≤104,1≤m≤2×104,1≤k≤100,1≤ui,vi≤n,0≤ai≤106
三、题目分析
- 完成题目一开始应该去尝试简化题目,将其转化为熟悉且简单的模型。如果不考虑 a i a_i ai 和 k k k 的非负整数倍,那么这将是一个很简单的单源最短路题目
- 根据题目给的特殊数据提示,我们先考虑 a i = 0 a_i=0 ai=0 的情况
- 对于到达某一个点的两个时刻 x , k + x ( x < k ) x,k+x(x<k) x,k+x(x<k) 来说, k + x k+x k+x 一定不如 x x x 。也就是说,对于 m o d k \mod k modk 同余的时刻来说,只需要保留其最短时刻即可。所以我们可以用一个数组 d i , j d_{i,j} di,j 来表示到第 i i i 个点时刻 m o d k = j \mod k=j modk=j 的最短时间,运行一遍 B F S BFS BFS 最后输出 d n , 0 d_{n,0} dn,0 即可。这样就能拿到 35 35 35 分了。
- 那么 a i ≠ 0 a_i\neq0 ai=0 会造成什么影响呢?其实我们完全可以推迟 k k k 的非负整数被的出发时间来满足这个要求。比如当前的边需要的时间是 w w w 大于目前时间 t i m tim tim ,那么就需要让出发时间延后 ⌈ w − t i m k ⌉ ⋅ k \lceil\frac{w-tim}{k}\rceil\cdot k ⌈kw−tim⌉⋅k 单位时间。
- 但是这样一来,延后出发时间之后不一定是最短的路径了,可能有其他的最短路径,那么就不能使用 B F S BFS BFS 每个点只更新一次的方式了。因为每个点需要多次更新,可以想到使用 d i j k s t r a dijkstra dijkstra 算法来解决这个最短路问题,因为时间复杂度的关系,我们这里需要使用堆优化,利用
set或者priority_queue。 - 时间复杂度 O ( n k log n k ) O(nk\log {nk}) O(nklognk)
四、正解程序
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <queue>using namespace std;
typedef long long ll;
const ll maxn=20010;
struct node
{ll v,w;ll next;
}e[2*maxn];
ll p[maxn],t=0;ll d[maxn][110];
bool vis[maxn][110];void insert(ll u,ll v,ll w)
{e[t].v=v;e[t].w=w;e[t].next=p[u];p[u]=t++;
}
struct New
{ll id,mod,len;bool operator<(const New &x) const{return len>x.len;}
};
int main()
{memset(p,-1,sizeof(p));memset(d,0x3f,sizeof(d));ll n,m,k;scanf("%lld%lld%lld",&n,&m,&k);for(ll i=1;i<=m;i++){ll u,v,w;scanf("%lld%lld%lld",&u,&v,&w);insert(u,v,w);}priority_queue<New> q;d[1][0]=0;q.push({1,0,d[1][0]});while(!q.empty()){ll u=q.top().id,mod=q.top().mod;q.pop();if(vis[u][mod])continue;vis[u][mod]=true;for(ll i=p[u];i!=-1;i=e[i].next){ll v=e[i].v,w=e[i].w;ll tim=d[u][mod],now=(mod+1)%k;if(tim<w)tim+=(w-tim+k-1)/k*k;if(d[v][now]>tim+1){d[v][now]=tim+1;q.push({v,now,d[v][now]});}}}if(d[n][0]>1e18)d[n][0]=-1;printf("%lld\n",d[n][0]);return 0;
}
相关文章:

CSP-J 2023真题解析
T1 小苹果 一、题目链接 P9748 [CSP-J 2023] 小苹果 二、题目大意 现有 n n n 个苹果从左到右排成一列,编号为从 1 1 1 到 n n n。 每天都会从中拿走一些苹果。拿取规则是,从左侧第 1 1 1 个苹果开始、每隔 2 2 2 个苹果拿走 1 1 1 个苹果。随…...
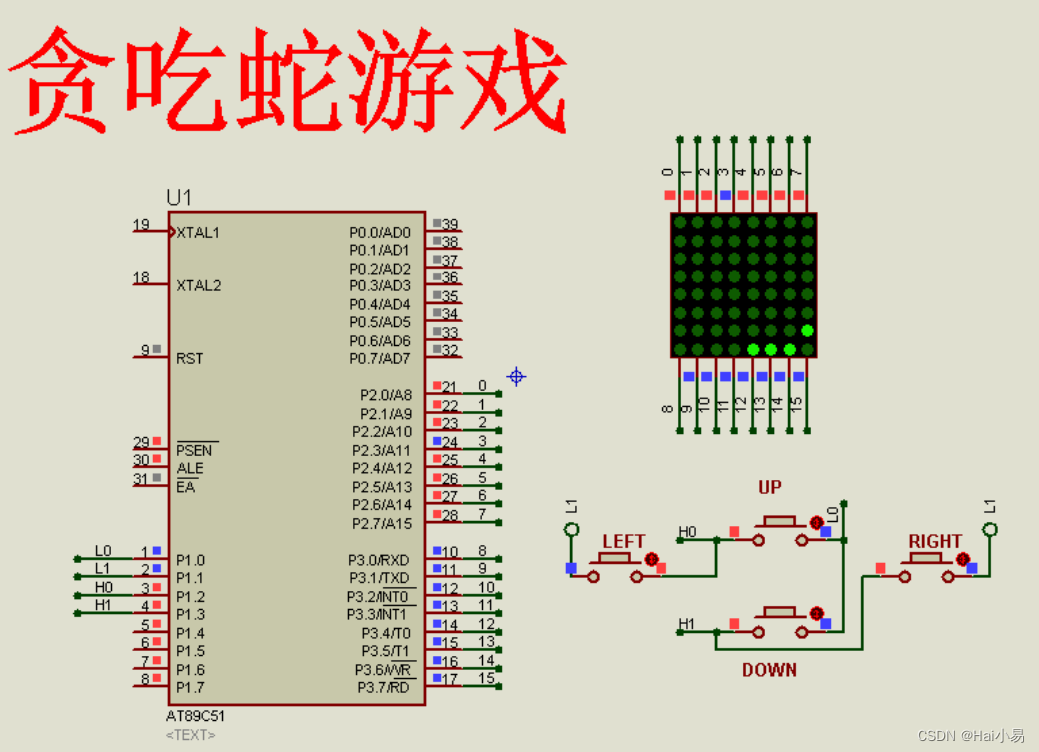
【Proteus仿真】【51单片机】贪吃蛇游戏
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用8*8LED点阵、按键模块等。 主要功能: 系统运行后,可操作4个按键控制小蛇方向。 二、软件设计 /* 作者:嗨小易…...
)
Android 原生定位开发(解决个别手机定位失败问题)
文章目录 前言一、实现步骤二、使用步骤1.服务启动工具类2.实现LocationService 总结 前言 在android开发中地图和定位是很多软件不可或缺的内容,这些特色功能也给人们带来了很多方便。定位一般分为三种发方案:即GPS定位、Google网络定位以及基站定位。…...

uni-app 中如何实现数据组件间传递?
在 uni-app 中,实现数据组件间传递可以使用 Props 或 Vuex。 Props 是一种组件通信的方式,通过向子组件传递数据来实现组件间的数据传递。下面是一个示例: 父组件: <template><child :message"hello">&l…...
SpringBoot整合自签名SSL证书,转变HTTPS安全访问(单向认证服务端)
前言 HTTP 具有相当优秀和方便的一面,然而 HTTP 并非只有好的一面,事物皆具两面性,它也是有不足之处的。例如: 通信使用明文(不加密),内容可能会被窃听。不验证通信方的身份,因此有可能会遭遇…...

k8s:endpoint
在 Kubernetes 中,Endpoint 是一种 API 对象,它用于表示集群内某个 Service 的具体网络地址。换句话说,它连接到一组由 Service 选择的 Pod,从而使它们能够提供服务。每个 Endpoint 对象都与相应的 Service 对象具有相同的名称&am…...
最新版星火官方搬运工具6.0,高级搬运,100%过原创,短视频上热门搬运软件黑科技【搬运脚本+使用技术教程】
软件介绍: 高级搬运,条条过原创 短视频暴力热门搬运黑科技 自研摄像头内录突破性技术6.0 无需任何繁琐准备工作安装即用 无需复杂售后培训看教程即可学会 直装直用自研技术更好卖 无需root 无需框架 更方便 无需xposed 无需vcam更安全 适配99%以…...
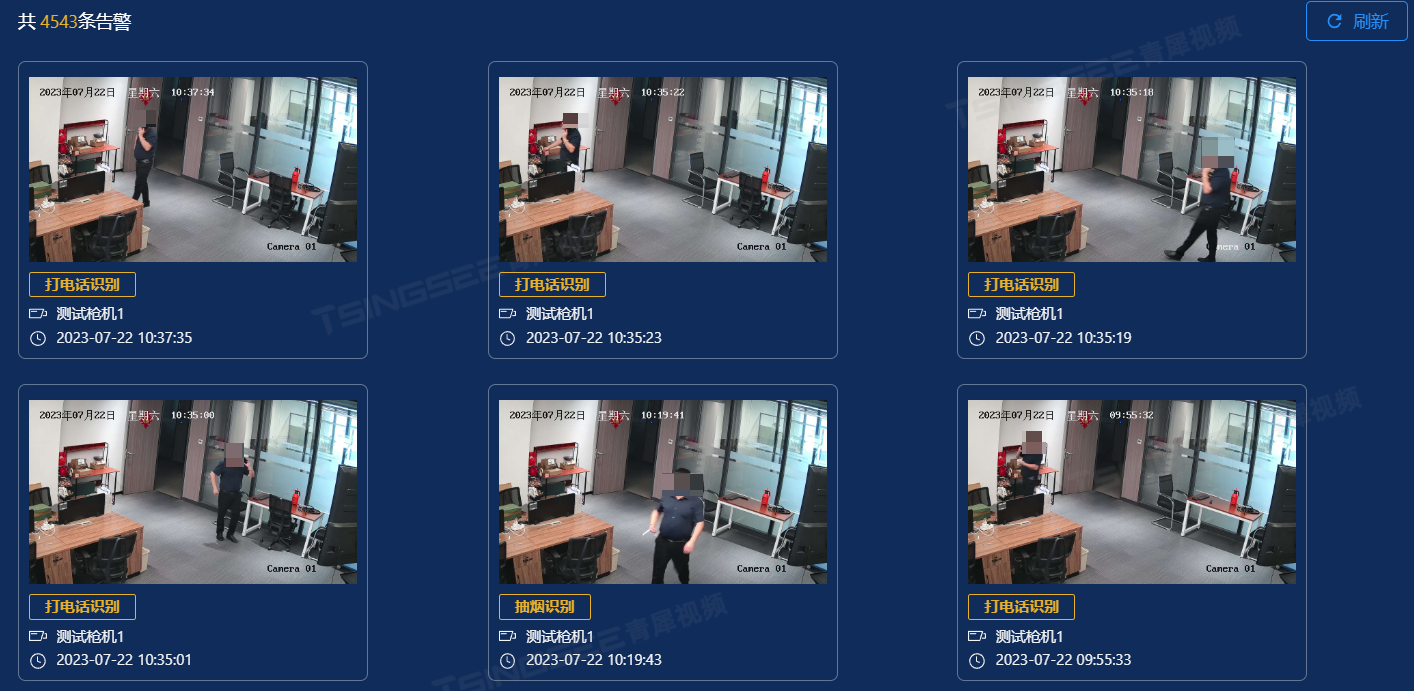
轧钢厂安全生产方案:AI视频识别安全风险智能监管平台的设计
一、背景与需求 轧钢厂一般都使用打包机对线材进行打包作业,由于生产需要,人员需频繁进入打包机内作业,如:加护垫、整包、打包机检修、调试等作业。在轧钢厂生产过程中,每个班次生产线材超过300件,人员在一…...

Linux Dotnet 程序堆栈监控
# 查看进程 dotnet-stack ps #显示如下2014067 dotnet /usr/share/dotnet/dotnet k1 --LogLevel4 2014087 dotnet /usr/share/dotnet/dotnet --LogLevel4 2014089 dotnet /usr/share/dotnet/dotnet --LogLevel4 # 根据PID查看这个进程每个线程的堆栈 dotnet-stack repor…...

后端设计PG liberty的作用和增量式生成
Liberty(俗称LIB和DB),是后端设计中重要的库逻辑描述文件,这里边包含了除过physical(当然也有一点点涉及)以外所有的信息,对整个后端设计实现有非常大的作用。借此机会,一起LIB做一个…...
Linux 安装 RocketMq
RocketMq是阿里出品(基于MetaQ)的开源中间件,已捐赠给Apache基金会并成为Apache的顶级项目。基于java语言实现,十万级数据吞吐量,ms级处理速度,分布式架构,功能强大,扩展性强。 官网…...

大数据Doris(十六):Doris表的数据划分
文章目录 Doris表的数据划分 一、Partition 二、 Bucket 三、PROPERTIES 四、 ENGINE Doris表的数据划分 Doris支持单分区和复合分...

管理文件:文件批量重命名,轻松删除文件名中的空格
在文件管理中,我们经常会遇到文件名中带有空格的情况。这些空格可能会使文件在某些情况下难以被正确识别或使用,因此我们需要掌握一些技巧来轻松删除文件名中的空格。现在使用云炫文件管理器批量重命名进行批量处理。以下是如何操作的步骤详解࿱…...
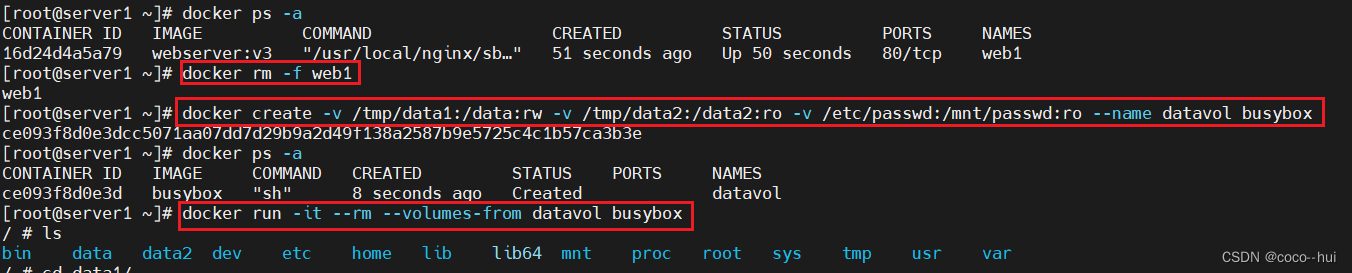
Docker容器技术实战3
8、docker原生网络 Docker原生网络基于Linux桥接技术和虚拟网络接口,使用了Linux内核的网络功能。每个Docker容器都有自己的网络命名空间,这使得容器之间可以使用独立的IP地址,并隔离了容器的网络栈。 当创建一个Docker原生网络时ÿ…...

数字处理-第10届蓝桥杯省赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第3讲。 数字处理ÿ…...

Go并发编程
一、goroutine 和 通道 在Go语言中,每一个并发执行的活动成为goroutine。通道则是每一个goroutine之间传递消息的工具。 1、Goroutine 在一个Go程序中,只有一个主Goroutine来调用main函数。生成新的goroutine也十分简单,例如有一个函数&…...

Nignx及负载均衡动静分离
核心要点:部署后台项目 1.配置jdk环境 1.先将jdk的Linux版本的压缩包上传虚拟机中服务器 2.解压上传的jdk压缩包 tar -zxvf jdk.gz 3.先进入jdk的解压目录,再通过pwd查看当前解压包的路径 4.将 解压包路径 配置到 /etc/profile 5…...

HDFS架构介绍
数新网络_让每个人享受数据的价值浙江数新网络有限公司是一家开源开放、专注于云数据智能操作系统和数据价值流通的服务商。公司自主研发的DataCyber云数据智能操作系统,主要包括数据平台CyberData、人工智能平台CyberAI、数据智能引擎CyberEngine、数据安全平台Cyb…...

微信小程序提示确认框 wx.showModal
核心实现代码如下 wx.showModal({ title: 确认, content: 确定要删除吗?, success (res) { if (res.confirm) { console.log(用户点击确定) } else if (res.cancel) { console.log(用户点击取消) } } })title 是确认框的标题,content 是确认…...
如何设置OBS虚拟摄像头给钉钉视频会议使用
环境: OBS Studio 29.1.3 Win10 专业版 钉钉7.1.0 问题描述: 如何设置OBS虚拟摄像头给钉钉视频会议使用 解决方案: 1.打开OBS 底下来源这添加视频采集设备 选择OBS虚拟摄像头 2.源那再建一个图像,随便选一张图片 3.点击虚…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...
