【数据结构】树家族
目录
- 树的相关术语
- 树家族
- 二叉树
- 霍夫曼树
- 二叉查找树 BST
- 平衡二叉树 AVL
- 红黑树
- 伸展树
- 替罪羊树
- B树
- B+树
- B* 树

当谈到数据结构中的树时,我们通常指的是一种分层的数据结构,它由节点(nodes)组成,这些节点之间以边(edges)相连。树的一个重要特性是它们具有一个根节点(root),它位于树的顶部,并且每个节点都有一个父节点(parent)以及零个或多个子节点(children)。树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合。
树的相关术语
根节点(Root):树的顶层节点,它没有父节点,是树的起点。父节点(Parent):一个节点的直接上级节点。子节点(Children):一个节点的直接下级节点。叶子节点(Leaf):没有子节点的节点称为叶子节点,它们位于树的末端。深度(Depth):一个节点的深度指的是从根节点到该节点的唯一路径的边数。高度(Height):树的高度是指树中任意节点的最大深度。子树(Subtree):一个节点及其所有子孙节点构成的集合,也是一个树。节点的度(Degree):一个节点拥有的子节点数目。树的度(Degree of Tree):树中节点的最大度数。层级(Level):根节点在第一层,其子节点在第二层,以此类推。兄弟节点(Siblings):具有相同父节点的节点称为兄弟节点。有序树与无序树:如果树中的节点是按照一定的顺序排列的,那么称它为有序树,否则称为无序树。
树家族

二叉树
 二叉树的任意节点至多包含两棵子树。
二叉树的任意节点至多包含两棵子树。
二叉树遍历:
二叉树的遍历是指从二叉树的根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点被访问一次,且仅被访问一次。二叉树的访问次序可以分为四种:
前序遍历 中序遍历 后序遍历 层次遍历

| 满二叉树 | 除了子结点之外的每一个结点都有两个孩子,每一层(当然包含最后一层)都被完全填充。 |
|---|---|
| 完全二叉树 | 除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左对齐。 |
| 严格二叉树 | 除了叶子结点之外的每一个结点都有两个孩了结点。 |
霍夫曼树

霍夫曼树的构建过程是基于一个给定的字符集合,每个字符都有一个权值(通常是它在文本中出现的频率)。构建霍夫曼树的目标是使得权值较大的字符在树中的深度相对较小,从而实现了最优前缀编码。霍夫曼编码可以借助霍夫曼树实现。
二叉查找树 BST

- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
平衡二叉树 AVL

平衡二叉树是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,同时,平衡二叉树必定是二叉搜索树。
平衡二叉树是一棵相对平衡的树,它的高度近似于 l o g 2 ( n ) log₂(n) log2(n),其中 n 是节点的数量。
平衡二叉树又称为AVL树,得名于其发明者 Adelson-Velsky 和 Landis。

AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
AVL树是一种特殊的BST树,它满足以下额外的条件:
- 每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1,平衡因子 = | 左子树高度 - 右子树高度 |
在一些情况下,添加删除会打破AVL树的自平衡性。所以 AVL树定义了旋转操作, 在平衡因子大于等于2时, AVL树会旋转来调整树的结构, 来重新满足平衡因子小于2。
AVL树适合用于插入删除次数比较少,但查找多的情况。
红黑树

红黑树和AVL树一样,也是自平衡二叉查找树。
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是红色或黑色。
- 根节点是黑色。
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
我们构建红黑树的过程是通过逐个插入新节点来完成的,在插入节点时,初始化根节点为黑节点,随后插入子节点时,初始为红色,然后通过修改颜色和旋转节点来完成平衡,最终使一棵子树完成平衡操作。
伸展树
伸展树是二叉查找树,满足左子树的key<=根节点的<=右子树的key的特点。不保证树是平衡的,但各种操作的平摊的复杂度是logn。从效率上上和平衡树的效率差不多。从编码复杂度上伸展树比红黑树和AVL简单了很多。
伸展树的思想:二八原则 ,也就是把那些访问频率高的的字段尽可能移到离根节点近的位置,所以每次访问节点都会通过各种旋转的方法将访问节点旋转到根节点。

替罪羊树
替罪羊树是计算机科学中,一种基于部分重建的自平衡二叉搜索树。在替罪羊树上,插入或删除节点的平摊最坏时间复杂度是O(log n),搜索节点的最坏时间复杂度是O(log n)。
在非平衡的二叉搜索树中,每次操作以后检查操作路径,找到最高的满足max(size(son_L),size(son_R))>alpha*size(this)的结点,重建整个子树。这样就得到了替罪羊树,而被重建的子树的原来的根就被称为替罪羊节点。
替罪羊树替罪羊树是一棵自平衡二叉搜索树,由ArneAndersson提出。替罪羊树的主要思想就是将不平衡的树压成一个序列,然后暴力重构成一颗平衡的树。
B树
一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树,或者是满足下列性质的树:
- 根结点至少有两个子女;
- 每个非根节点所包含的关键字个数 j 满足: ⌈ m 2 ⌉ − 1 < = j < = m − 1 \left \lceil \frac{m}{2} \right \rceil - 1 <= j <= m - 1 ⌈2m⌉−1<=j<=m−1;
- 除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1,故内部子树个数 k 满足: ⌈ m 2 ⌉ < = k < = m \left \lceil \frac{m}{2} \right \rceil <= k <= m ⌈2m⌉<=k<=m;
- 所有的叶子结点都位于同一层。

B树(B-Tree)是一种自平衡的树,它是一种多路搜索树(并不是二叉的),能够保证数据有序。同时它还保证了在查找、插入、删除等操作时性能都能保持在O(logn),为大块数据的读写操作做了优化,同时它也可以用来描述外部存储(支持对保存在磁盘或者网络上的符号表进行外部查找)
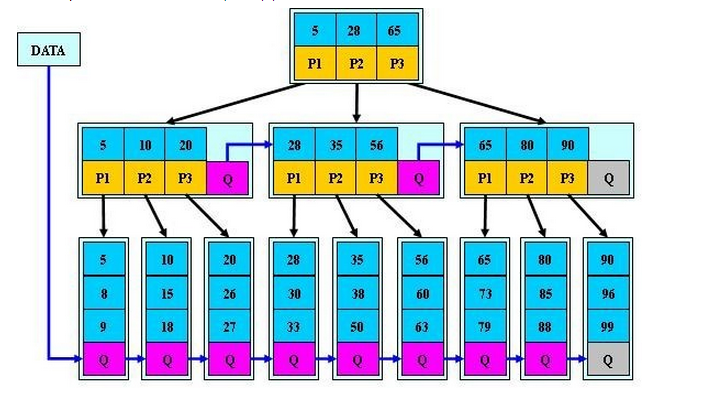
B+树

B+树是在B树的基础上又一次的改进,其主要对两个方面进行了提升,一方面是查询的稳定性,另外一方面是在数据排序方面更友好。
B+树构建规则:
- B+树的非叶子节点不保存具体的数据,而只保存关键字的索引,而所有的数据最终都会保存到叶子节点。因为所有数据必须要到叶子节点才能获取到,所以每次数据查询的次数都一样,这样一来B+树的查询速度也就会比较稳定,而B树的查找过程中,不同的关键字查找的次数很有可能都是不同的(有的数据可能在根节点,有的数据可能在最下层的叶节点)。
- B+树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针。因为叶子节点都是有序排列的。
- 非叶子节点的子节点数=关键字数;另一种为非叶节点的关键字数=子节点数-1。这里有两种算法的实现方式,虽然他们数据排列结构不一样,但其原理还是一样的Mysql 的B+树是用第一种方式实现。
B树与B+树的比较:
-
B+树查询速度更稳定:B+所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同所以查询速度要比B树更稳定。
-
B+树天然具备排序功能:B+树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高。
-
B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,而不需要像B树一样需要对每一层进行遍历,这有利于数据库做全表扫描。
B树相对于B+树的优点是,如果经常访问的数据离根节点很近,而B树的非叶子节点本身存有关键字和数据,所以在查询这种数据检索的时候会要比B+树快。
B* 树
B*树又是对B+数的再一次改进。
两者有以下两方面的不同:
- 首先是关键字个数限制问题,B+树初始化的关键字初始化个数是 ⌈ m 2 ⌉ \left \lceil \frac{m}{2} \right \rceil ⌈2m⌉,b*树的初始化个数为 ⌈ 2 m 3 ⌉ \left \lceil \frac{2m}{3} \right \rceil ⌈32m⌉
- B+树节点满时就会分裂,而B*树节点满时会检查兄弟节点是否满(因为每个节点都有指向兄弟的指针),如果兄弟节点未满则向兄弟节点转移关键字,如果兄弟节点已满,则从当前节点和兄弟节点各拿出1/3的数据创建一个新的节点出来。
相关文章:

【数据结构】树家族
目录 树的相关术语树家族二叉树霍夫曼树二叉查找树 BST平衡二叉树 AVL红黑树伸展树替罪羊树 B树B树B* 树 当谈到数据结构中的树时,我们通常指的是一种分层的数据结构,它由节点(nodes)组成,这些节点之间以边(…...

Vert.x学习笔记-Vert.x的基本处理单元Verticle
Verticle介绍 Verticle是Vert.x的基本处理单元,Vert.x应用程序中存在着处理各种事件的处理单元,比如负责HTTP API响应请求的处理单元、负责数据库存取的处理单元、负责向第三方发送请求的处理单元。Verticle就是对这些功能单元的封装,Vertic…...
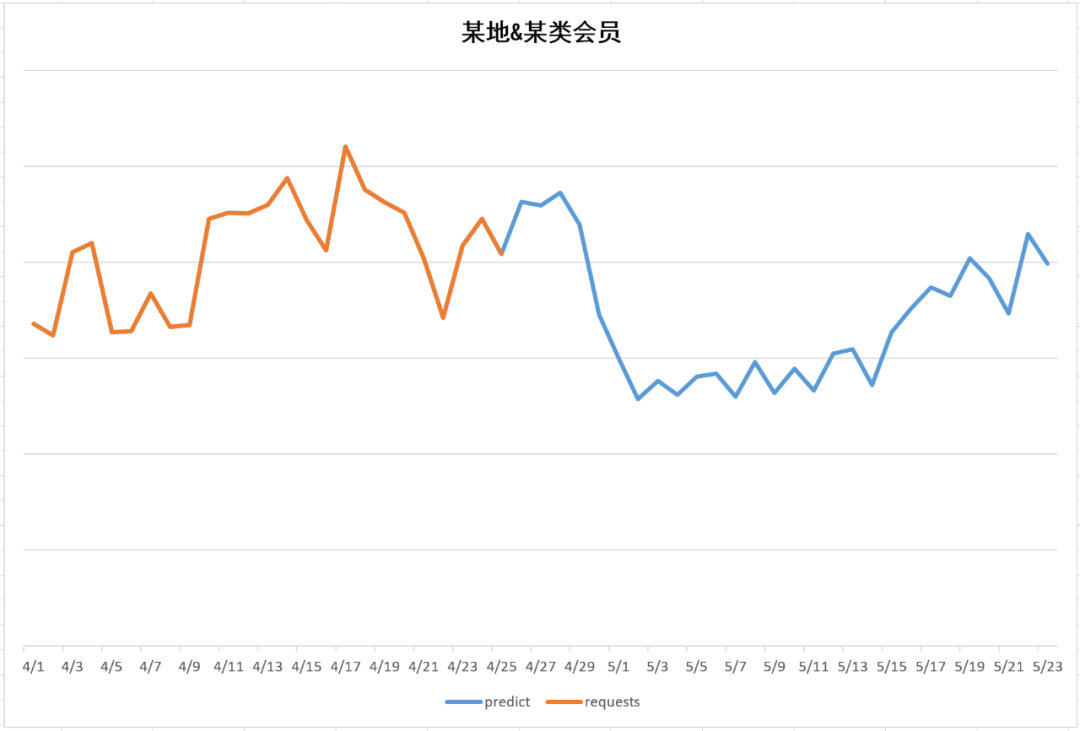
干货分享:基于 LSTM 的广告库存预估算法
近年来,随着互联网的发展,在线广告营销成为一种非常重要的商业模式。出于广告流量商业化售卖和日常业务投放精细化运营的目的,需要对广告流量进行更精准的预估,从而更精细的进行广告库存管理。 因此,携程广告纵横平台…...

dataframe删除某一列
drop import pandas as pd data {‘A’: [1, 2, 3], ‘B’: [4, 5, 6], ‘C’: [7, 8, 9]} df pd.DataFrame(data) #使用drop方法删除列 df df.drop(‘B’, axis1) # 通过指定列名和axis1来删除列 del import pandas as pd data {‘A’: [1, 2, 3], ‘B’: [4, 5, 6]…...

提升ChatGPT答案质量和准确性的方法Prompt engineering
文章目录 怎么获得优质的答案设计一个优质prompt的步骤:Prompt公式:示例怎么获得优质的答案 影响模型回答精确度的因素 我们应该知道一个好的提示词,要具备一下要点: 清晰简洁,不要有歧义; 有明确的任务/问题,任务如果太复杂,需要拆分成子任务分步完成; 确保prompt中…...
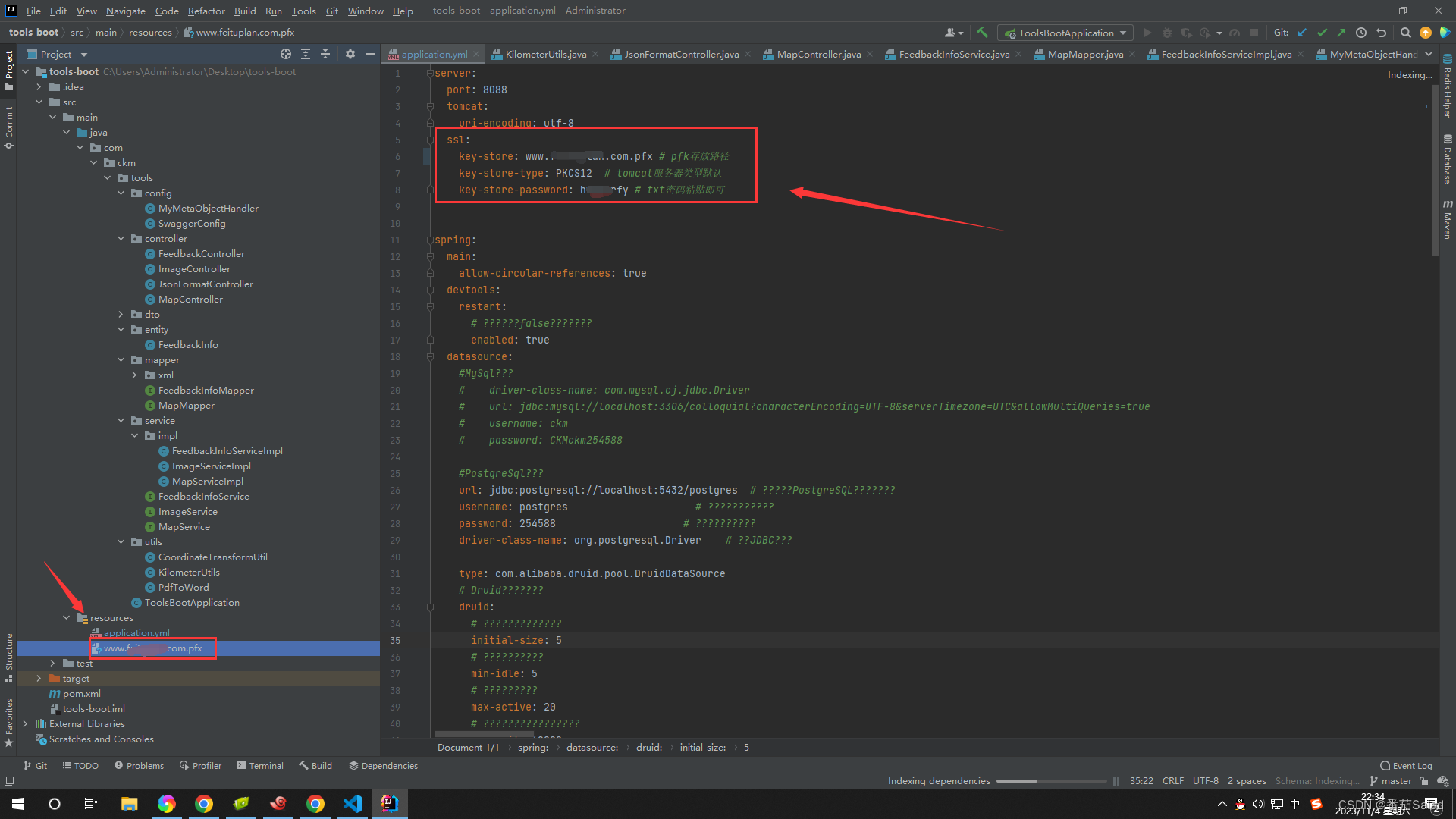
SpringBoot + Vue2项目打包部署到服务器后,使用Nginx配置SSL证书,配置访问HTTP协议转HTTPS协议
配置nginx.conf文件,这个文件一般在/etc/nginx/...中,由于每个人的体质不一样,也有可能在别的路径里,自己找找... # 配置工作进程的最大连接数 events {worker_connections 1024; }# 配置HTTP服务 http {# 导入mime.types配置文件…...

HTML 表格
<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>表格标签</title>/* <style>.yun {widt…...
试用 10 -- 安全性问题)
AIGC(生成式AI)试用 10 -- 安全性问题
上次遗留的问题:代码的安全性呢?下次找几个问题测试下看。 AI,你安全吗? AI生成的程序,安全吗? 也许这个世界最难做的事就是自己测试自己:测试什么?如何测? …...
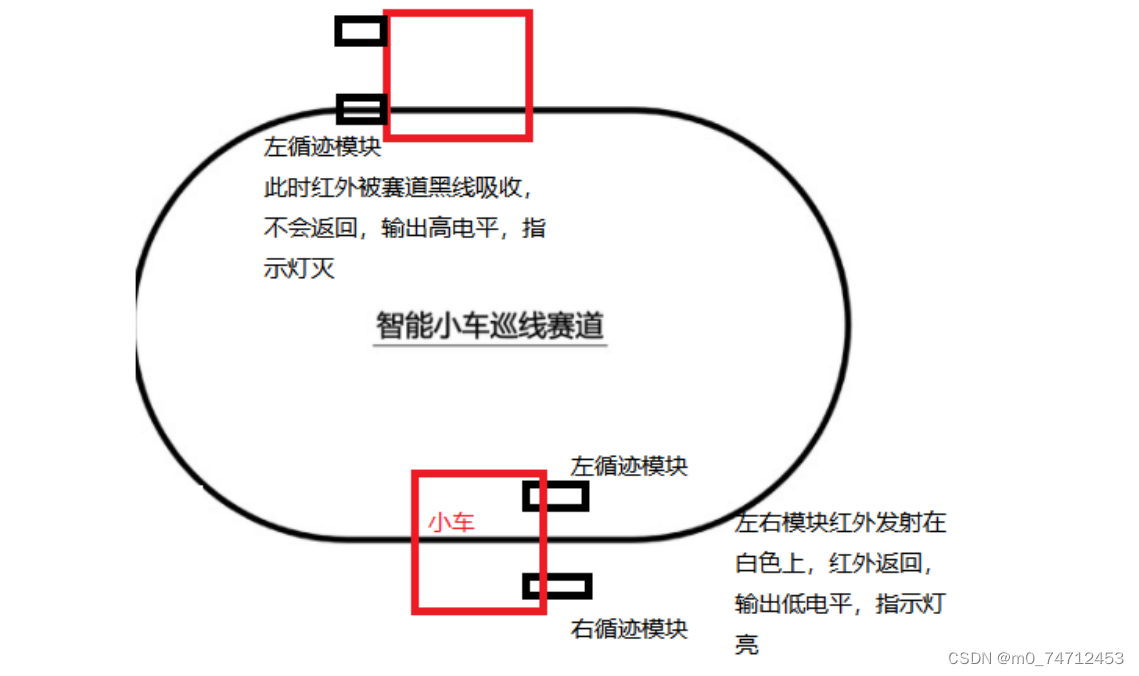
STM32循迹小车原理介绍和代码示例
目录 1. 循迹模块介绍 2. 循迹小车原理 3. 循迹小车核心代码 4. 循迹小车解决转弯平滑问题 1. 循迹模块介绍 TCRT5000传感器的红外发射二极管不断发射红外线当发射出的红外线没有被反射回来或被反射回来但强度不够大时红外接收管一直处于关断状态,此时模块的输出…...

Nginx 配置详细讲解
Nginx.conf 配置文件分为三部分,分别为main块、events块、http块(http块又包含server块和location块),如下图。 第一部分:main块(全局块) main块主要是设置一些影响Nginx服务器整体运行的配置指令,主要包括…...
)
gdb 日志记录不显示到屏幕的方法(gdb13最新版)
tags: gdb categories: [Debug] 写在前面 gdb 的更新好快啊… 之前的选项都有改动了, 比如 logging… 需要屏幕重定向不能简单设置: set logging on set logging redirect on了, 而是要多开一个配置, 踩坑了 方法 在此之前先看一下我的 gdbinit 配置: set debuginfod e…...
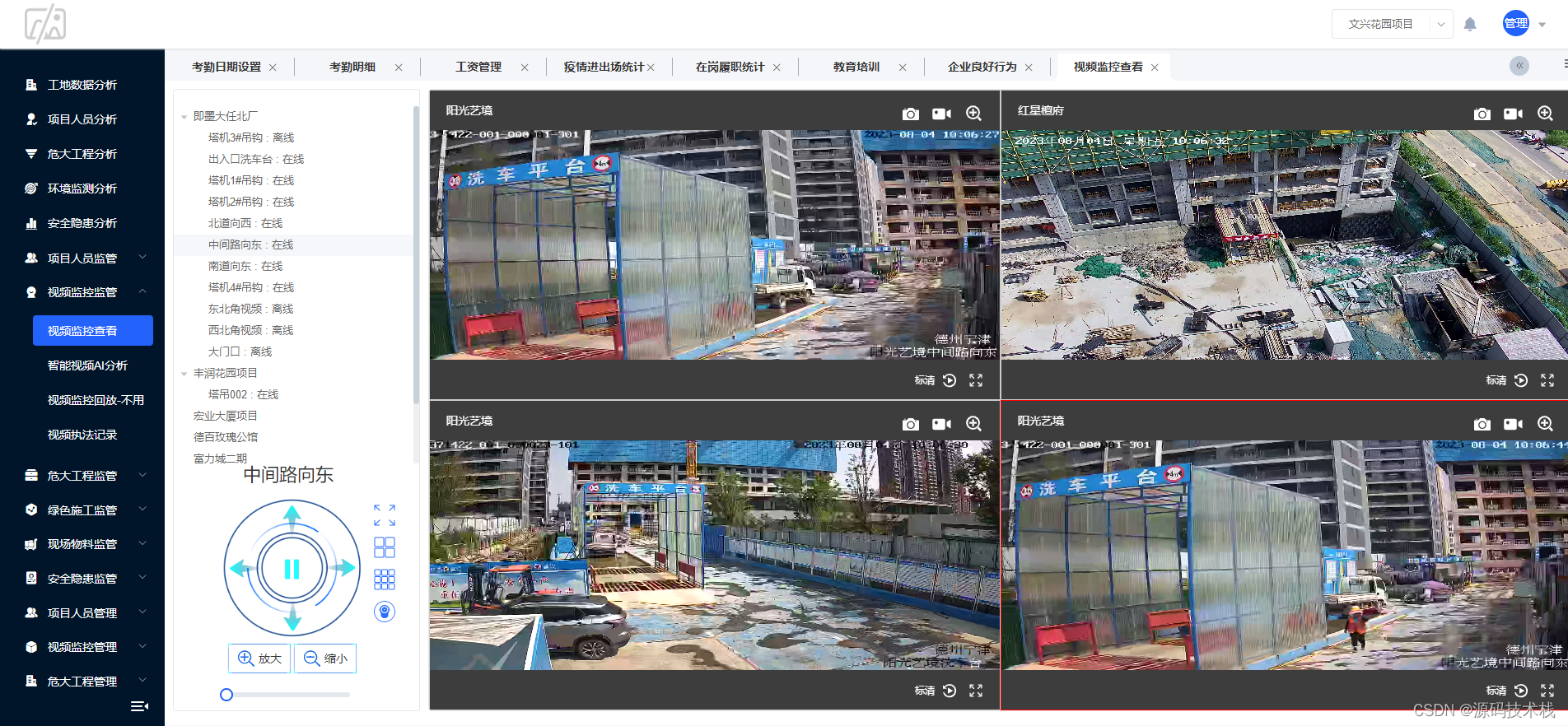
JAVA智慧工地管理系统源码基于微服务
智慧工地是将互联网的理念和科技引入施工现场,从施工现场源头抓起,大程度的收集人员、安全、环境、质量等关键业务数据。通过结合物联网、大数据、互联网、云计算等技术建立云端大数据管理平台,形成端云大数据的体系与模式,这就是…...
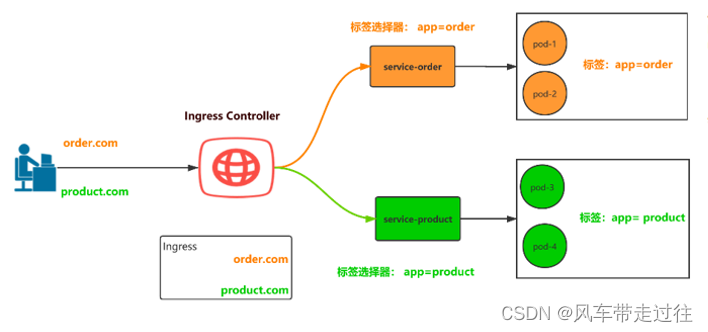
学习笔记三十四:Ingress和 Ingress Controller概述
Ingress和 Ingress Controller概述 回顾service四层负载在k8s中为什么要做负载均衡Service不足之处四层负载和七层负载的区别OSI七层模型: Ingress介绍Ingress Controller介绍Ingress-controller 作用Ingress和Ingress Controller总结使用Ingress Controller代理k8s…...

Webpack的Tree Shaking。它的作用是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...
研发效能DevOps: Git安装
目录 一、理论 1.Git 2.Git 工具 二、实验 1.Git安装 2.配置Git 3. VS Code加载Git 一、理论 1.Git (1)简介 Git 是一个分布式版本控制及源代码管理工具;Git 可以为你的项目保存若干快照,以此来对整个项目进行版本管理。 Git 是一个…...
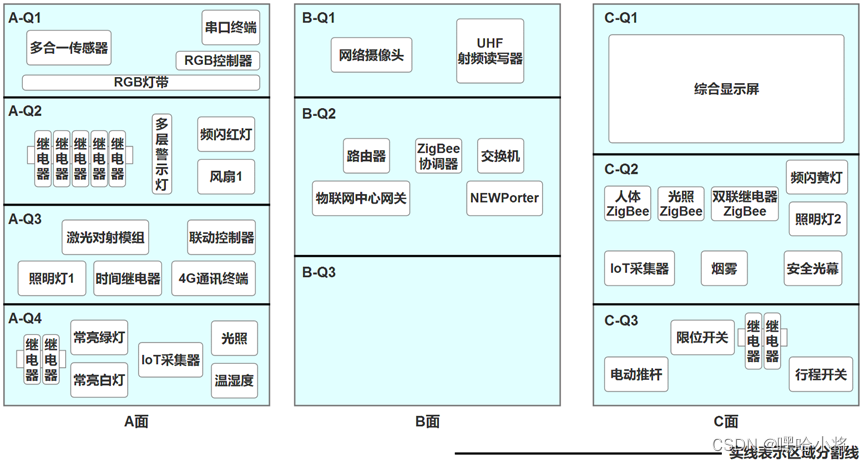
ZZ038 物联网应用与服务赛题第D套
2023年全国职业院校技能大赛 中职组 物联网应用与服务 任 务 书 (D卷) 赛位号:______________ 竞赛须知 一、注意事项 1.检查硬件设备、电脑设备是否正常。检查竞赛所需的各项设备、软件和竞赛材料等; 2.竞赛任务中所使用的各类软件工具、软件安装文件等,都…...
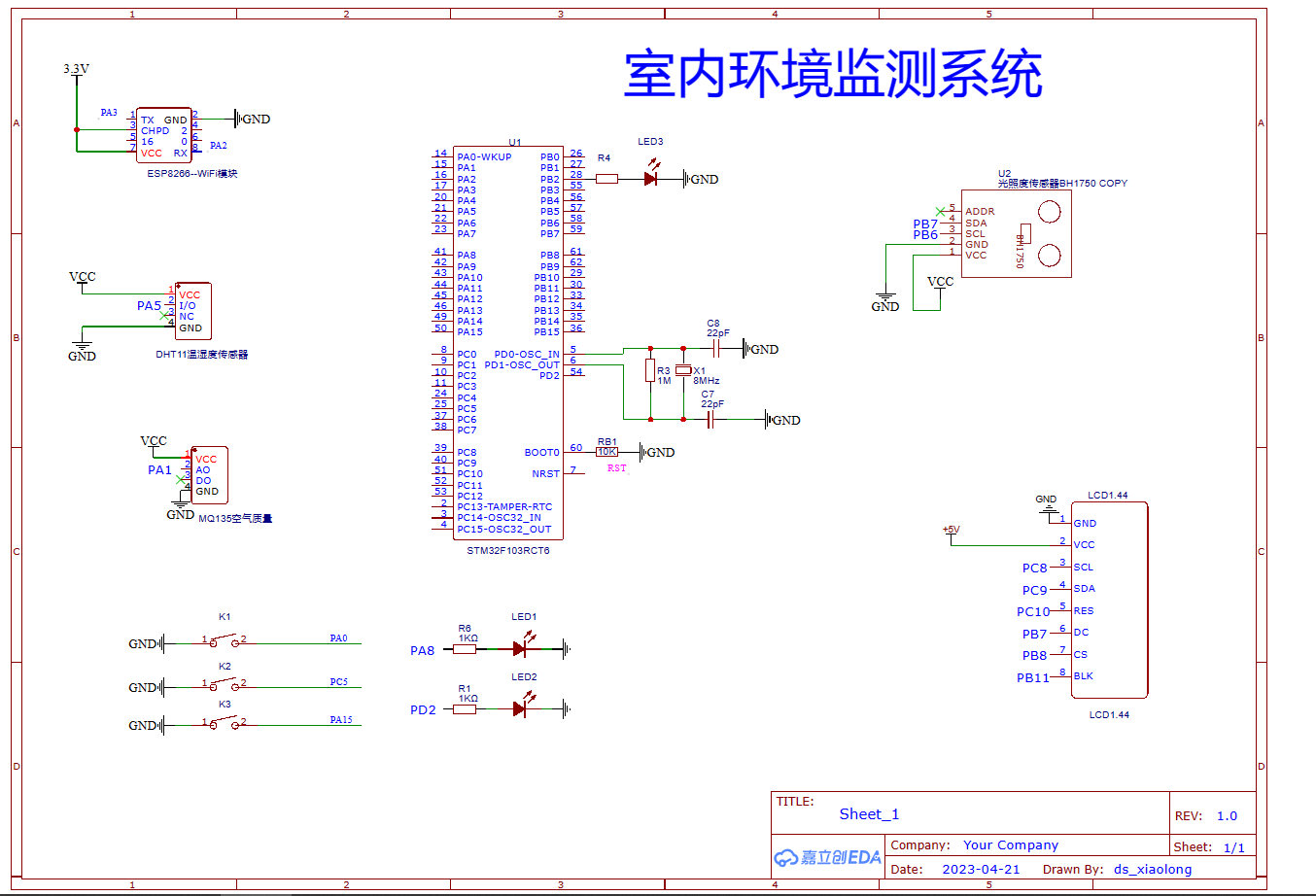
基于STM32设计的室内环境监测系统(华为云IOT)_2023
一、设计需求 基于STM32+华为云物联网平台设计一个室内环境监测系统,以STM32系列单片机为主控器件,采集室内温湿度、空气质量、光照强度等环境参数,将采集的数据结果在本地通过LCD屏幕显示,同时上传到华为云平台并将上传的数据在Android移动端能够实时显示、查看。 【1…...
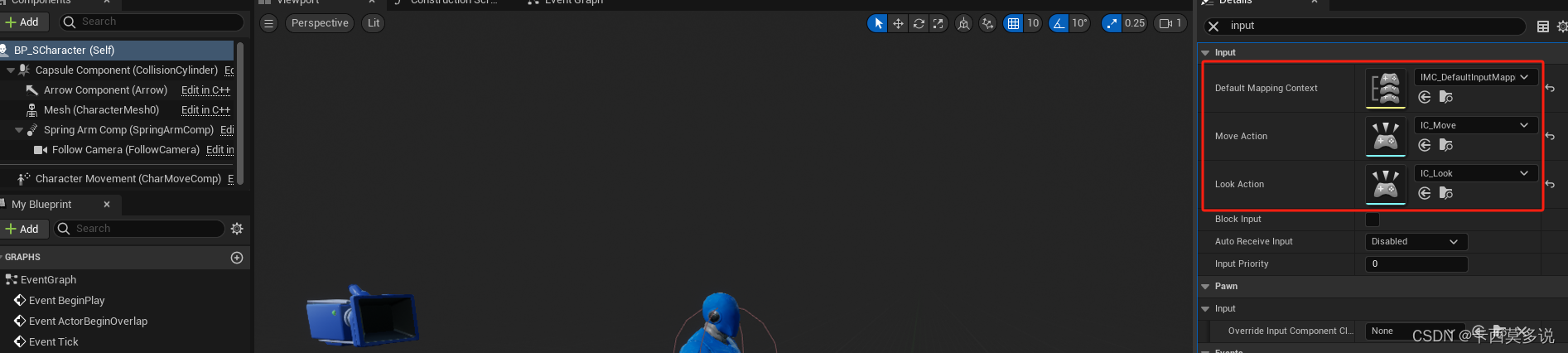
UE5C++学习(一)--- 增强输入系统
一、关于增强输入系统的介绍 增强输入系统官方文档介绍 二、增强输入系统的具体使用 注:在使用方面,不会介绍如何创建项目等基础操作,如果还没有UE的使用基础,可以参考一下我之前UE4的文章,操作差别不会很大。 如上…...

好物周刊#29:项目管理软件
https://github.com/cunyu1943/JavaPark https://yuque.com/cunyu1943 村雨遥的好物周刊,记录每周看到的有价值的信息,主要针对计算机领域,每周五发布。 一、项目 1. HelloGithub 分享 GitHub 上有趣、入门级的开源项目。每月 28 号以月刊…...

玻色量子“天工量子大脑”亮相中关村论坛,大放异彩
2023年5月25日至30日,2023中关村论坛(科博会)在北京盛大召开。中关村论坛(科博会)是面向全球科技创新交流合作的国家级平台行业盛会,由科技部、国家发展改革委、工业和信息化部、国务院国资委、中国科学院、…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...
