数组初始化方式与decimal.InvalidOperation
数组初始化方式与decimal.InvalidOperation
- 调用函数
- 主函数: 数组声明不同带来的报错与否
- 1. 报错decimal.InvalidOperation的数组初始化版本
- 2. 可行的初始化版本
- 输出结果
- 1. 报错时的内容
- 2. 正常的输出计算结果
- 原因(是否是数组与列表不同引起(?
调用函数
import scipy.misc
import numpy as np
from decimal import *x = [i for i in range(10, 110, 10)]
print(x)def countA_with_n(n):global Aif n==0:A[n]=1else:for i in range(1, n+1):if A[n-i]==0:A[n-i]=countA_with_n(n - i)#t=(-1) ** (i + 1) * 2 ** ((n - i) * i)* scipy.misc.comb(n, i)*A[n-i]A[n] = Decimal(A[n]) + Decimal((-1) ** (i + 1)) * Decimal(2 ** ((n - i) * i)) * Decimal(scipy.misc.comb(n, i)) *Decimal(A[n-i])#A[n]+=treturn A[n]主函数: 数组声明不同带来的报错与否
1. 报错decimal.InvalidOperation的数组初始化版本
#主函数
for a in x:A = np.zeros(a+1) #前40可以计算,50时会报错‘decimal.InvalidOperation: [<class 'decimal.InvalidOperation'>]’#A = [0]*(a+1) #可行的声明方法print(str(a),str(countA_with_n(a)))
2. 可行的初始化版本
for a in x:A = [0]*(a+1) #可行的声明方法print(str(a),str(countA_with_n(a)))
输出结果
1. 报错时的内容
10 4.175098976430598e+18
20 2.3448804510510887e+72
30 2.7148544371675283e+158
C:...py:18: DeprecationWarning: `comb` is deprecated!Importing `comb` from scipy.misc is deprecated in scipy 1.0.0. Use `scipy.special.comb` instead.A[n] = Decimal(A[n]) + Decimal((-1) ** (i + 1)) * Decimal(2 ** ((n - i) * i)) * Decimal(scipy.misc.comb(n, i)) *Decimal(A[n-i])
40 1.1241428263057385e+276
Traceback (most recent call last):File "C:xxx.py", line 65, in <module>print(str(a),str(countA_with_n(a)))File "...", line 16, in countA_with_nA[n-i]=countA_with_n(n - i)File "...", line 16, in countA_with_nA[n-i]=countA_with_n(n - i)File "...", line 16, in countA_with_nA[n-i]=countA_with_n(n - i)[Previous line repeated 2 more times]File "...", line 18, in countA_with_nA[n] = Decimal(A[n]) + Decimal((-1) ** (i + 1)) * Decimal(2 ** ((n - i) * i)) * Decimal(scipy.misc.comb(n, i)) *Decimal(A[n-i])
decimal.InvalidOperation: [<class 'decimal.InvalidOperation'>]
2. 正常的输出计算结果
DeprecationWarning: `comb` is deprecated!Importing `comb` from scipy.misc is deprecated in scipy 1.0.0. Use `scipy.special.comb` instead.A[n] = Decimal(A[n]) + Decimal((-1) ** (i + 1)) * Decimal(2 ** ((n - i) * i)) * Decimal(scipy.misc.comb(n, i)) *Decimal(A[n-i])
10 4175098976430598143
20 2.344880451051088988152559846E+72
30 2.714854437167529438448086150E+158
40 1.124142826305737256464230893E+276
50 7.150572516568295733815015286E+424
60 4.231846207434397246471425291E+604
70 1.670508589429661015982839133E+815
80 3.469441880795996245588913622E+1056
90 3.173623968493402552666007937E+1328
100 1.113552460282985747462212849E+1631
原因(是否是数组与列表不同引起(?
参看 数组与列表的区别

相关文章:

数组初始化方式与decimal.InvalidOperation
数组初始化方式与decimal.InvalidOperation调用函数主函数: 数组声明不同带来的报错与否1. 报错decimal.InvalidOperation的数组初始化版本2. 可行的初始化版本输出结果1. 报错时的内容2. 正常的输出计算结果原因(是否是数组与列表不同引起(?…...
【Opencv-python】之入门安装
目录 一、安装Python 1. 登录官网https://www.python.org/downloads/ 2. 任选一个版本,下载Python 3. 安装Python 记得勾选下图的Add Python 3.6 PATH, 添加python到环境变量的路径,然后选择Install now编辑 4. 验证是否安装成功 5.退出 二、安装…...

MySQL进阶(二)
目录 1、视图 1、检查选项 2、视图的更新 3、视图作用 2、存储过程 1、语法 2、变量 1、系统变量 2、用户定义变量 3、局部变量 3、if 4、参数 5、case 6、循环 1、while 2、repeat 3、loop 7、游标、条件处理程序 8、存储函数 3、触发器 4、锁 1、全局锁 2、表级锁 …...
热爱所有热爱
想成为这样的一个人,在工作中是一名充满极客精神的Programmer,处理遇到的问题能够游刃有余,能够做出优雅的设计,写出一手优秀的代码,还有着充分的学习能力和业务能力,做一名职场中的佼佼者。 在工作之余还能…...
)
Redis学习之数据删除与淘汰策略(七)
这里写目录标题一、Redis数据特征二、过期数据三、过期数据删除策略3.1 数据删除策略的目标3.2 定时删除3.3 惰性删除3.4 定期删除3.5 删除策略对比3.6 实际应用四、数据淘汰策略4.1 淘汰策略概述4.2 策略配置一、Redis数据特征 Redis是一种内存级数据库,所有的数据…...

HashMap 面试专题
1、HashMap 的底层结构 ①JDK1.8 以前 JDK1.8 之前 HashMap 底层是 数组和链表 结合在一起使用也就是 链表散列。HashMap 通过 key 的hashCode 函数处理过后得到 hash 值,然后通过 (n - 1) & hash 判断当前元素存放的位置(这里的 n 指的是数组的长度…...
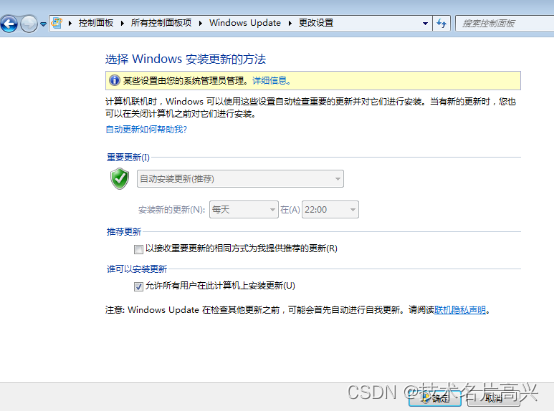
域组策略自动更新实验报告
域组策略自动更新实验报告 域组策略自动更新实验报告 作者: 高兴源 1要求、我公司为了完善员工的安全性和系统正常漏洞的维护,所以采用域组策略自动更新的方法来提高账户安全性,减少了用户的错误。 1.实验环境如下1台2008r2一台创建域,一台wi…...

Java自定义生成二维码(兼容你所有的需求)
1、概述作为Java开发人员,说到生成二维码就会想到zxing开源二维码图像处理库,不可否认的是zxing确实很强大,但是实际需求中会遇到各种各样的需求是zxing满足不了的,于是就有了想法自己扩展zxing满足历史遇到的各种需求,…...

Spring事务的隔离级别
事务隔离级别解决的是多个事务同时调⽤⼀个数据库的问题 事务传播机制解决的是⼀个事务在多个节点(⽅法)中传递的问题 事务的特性: 隔离性:多个事务在并发执行的时候,多个事务执行的一个行为模式,当一个事务执行的时候,另一个事务执行的一个行…...

JVM系统优化实践(4):以支付系统为例
您好,我是湘王,这是我的CSDN博客,欢迎您来,欢迎您再来~前面说过,JVM会将堆内存划分为年轻代、老年代两个区域。年轻代会将创建和使用完之后马上就要回收的对象放在里面,而老年代则将创建之后需要…...

16- TensorFlow实现线性回归和逻辑回归 (TensorFlow系列) (深度学习)
知识要点 线性回归要点: 生成线性数据: x np.linspace(0, 10, 20) np.random.rand(20)画点图: plt.scatter(x, y)TensorFlow定义变量: w tf.Variable(np.random.randn() * 0.02)tensor 转换为 numpy数组: b.numpy()定义优化器: optimizer tf.optimizers.SGD()定义损失: …...

无自动化测试系统设计方法论
灵活 敏捷 迭代。 自动化测试 辩思 测试必不可少 想想看没有充分测试的代码, 哪一次是一次过的? 哪一次不需要经历下测试的鞭挞? 不要以为软件代码容易改, 就对于质量不切实际的自信—那是自大! 不适用自动化测试的case 遗留系统。太多的依赖方, 不想用过多的mock > …...
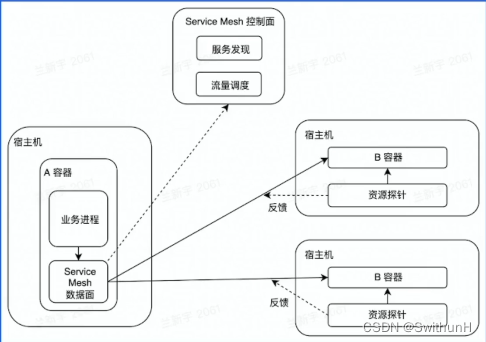
架构初探-学习笔记
1 什么是架构 有关软件整体结构与组件的抽象描述,用于指导软件系统各个方面的设计。 1.1 单机架构 所有功能都实现在一个进程里,并部署在一台机器上。 1.2 单体架构 分布式部署单机架构 1.3 垂直应用架构 按应用垂直切分的单体架构 1.4 SOA架构 将…...

在成都想转行IT,选择什么专业比较好?
很多创新型的互联网服务公司的核心其实都是软件,创新的基础、运行的支撑都是软件。例如,软件应用到了出租车行业,就形成了巅覆行业的滴滴;软件应用到了金融领域,就形成互联网金融;软件运用到餐饮行业,就形成美团;软件运…...
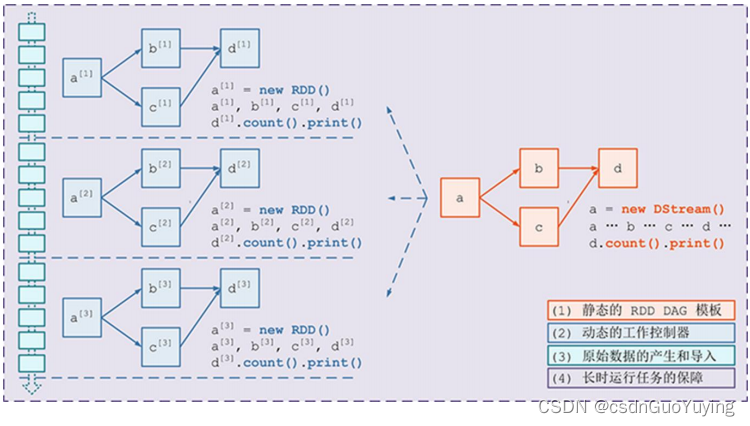
【Spark分布式内存计算框架——Spark Streaming】4.入门案例(下)Streaming 工作原理
2.3 Streaming 工作原理 SparkStreaming处理流式数据时,按照时间间隔划分数据为微批次(Micro-Batch),每批次数据当做RDD,再进行处理分析。 以上述词频统计WordCount程序为例,讲解Streaming工作原理。 创…...
2、算法先导---思维能力与工具
题目 碎纸片的拼接复原(2013B) 内容 破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。传统上,拼接复原工作需由人工完成,准确率较高,但效率很低。特别是当碎片数量巨大,人工拼接很难在短时…...

WordPress 函数:add_theme_support() 开启主题自定义功能(全面)
add_theme_support() 用于在我们的当前使用的主题添加一些特殊的功能,函数一般写在主题的functions.php文件中,当然也可以再插件中使用钩子来调用该函数,如果是挂在钩子上,那他必须挂在after_setup_theme钩子上,因为 i…...

Winform控件开发(16)——Timer(史上最全)
前言: Timer控件的作用是按用户定义的时间间隔引发事件的计时器,说的直白点就是,他就像一个定时炸弹一样到了一定时间就爆炸一次,区别在于定时炸弹炸完了就不会再次爆炸了,但是Timer这个计时器到了下一个固定时间还会触发一次,上面那张图片就是一个典型的计时器,该定时器…...

游戏高度可配置化:通用数据引擎(data-e)及其在模块化游戏开发中的应用构想图解
游戏高度可配置化:通数据引擎在模块化游戏开发中的应用构想图解 ygluu 码客 卢益贵 目录 一、前言 二、模块化与插件 1、常规模块化 2、插件式模块化(插件开发) 三、通用数据引擎理论与构成 1、名字系统(数据类型…...
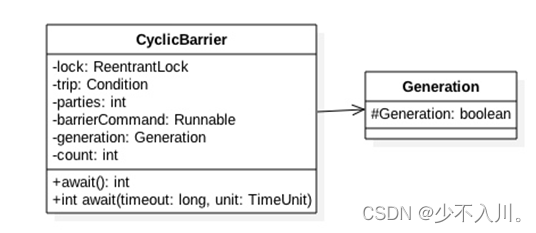
CountDownLatch与CyclicBarrier原理剖析
1.CountDownLatch 1.1 什么是CountDownLatch CountDownLatch是一个同步工具类,用来协调多个线程之间的同步,或者说起到线程之间的通信(而不是用作互斥的作用)。 CountDownLatch能够使一个线程在等待另外一些线程完成各自工作之…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
