线性回归与线性拟合的原理、推导与算法实现
关于回归和拟合,从它们的求解过程以及结果来看,两者似乎没有太大差别,事实也的确如此。从本质上说,回归属于数理统计问题,研究解释变量与响应变量之间的关系以及相关性等问题。而拟合是把平面的一系列点,用一条光滑曲线连接起来,并且让更多的点在曲线上或曲线附近。更确切的说,拟合是回归用到的一种数学方法,而拟合与回归的应用场合不同。
拟合常用的方法有最小二乘法、梯度下降法、高斯牛顿(即迭代最小二乘)、列-马算法。其中最最常用的就是最小二乘法。并且拟合可以分为线性拟合与非线性拟合,非线性拟合比较常用的是多项式拟合。根据自变量的个数,拟合也可以分为曲线拟合与曲面拟合等。
回归大多数采用最小二乘法。回归可以分为一元线性回归、一元非线性回归、多元线性回归、多元非线性回归等。
1、最小二乘法
无论是在高等数学、线性代数,还是数理统计,我们都可以看到最小二乘法的身影。只不过每一部分侧重点不同,最终是殊途同归的。但是建议用矩阵的方法来做,这样很便于理解,计算起来也很方便。
最小二乘法的基本思路是:确定函数f(x),使得各个点x1,x2..xn处的函数值偏差f(x1)-y1、f(x2)-y2...f(xn)-yn的平方和或绝对值和最小。如果是一元线性拟合(回归),我们可以设方程为f(x)=kx+b。
这时我们求得函数值偏差平方和为。为了求它的最小值,利用高数的方法,就可以使M分别对k和b的偏导为0,最终求解得方程组:
公式1 :
公式2 :
由式2括号内为0,则有b的表达式
公式3 :
将式(3)代入到式(2)中得到式(4)
公式4 :
整理式(4)我们可以得到k的表达式
公式5 :
如果用线性代数的角度来看其实矩阵表达更加简洁,我们最终需要寻找最佳的k和b :
公式6 :
写成矩阵的形式:
公式7 :
令 ,
,
我们可以写成矩阵形式:
公式8 :
我们要解K,这时候X如果是方阵那么自然的就可以左右两边同时乘X的逆,但是如果X不是方阵(行数大于列数),我们可以左右同乘以X的转置,转换为方阵再取逆(当然能取逆的前提是行列式不能为0),具体如下,求得的逆叫做伪逆:
公式9 : =>
=>
所以解得K的值:
公式10 :
2、matlab实现
现在有这么一组数据
| x | y |
|---|---|
| 0.1 | 1.7805 |
| 0.3 | 2.2285 |
| 0.4 | 2.3941 |
| 0.75 | 3.2226 |
| 0.9 | 3.5697 |
我们利用matlab进行绘制散点图查看一下
x=[0.1;0.3;0.4;0.75;0.9];
y=[1.7805;2.2285;2.3941;3.2226;3.5697];
plot(x,y,'o')
xlim([0,1]);
ylim([1.6,3.7]);
hold on;
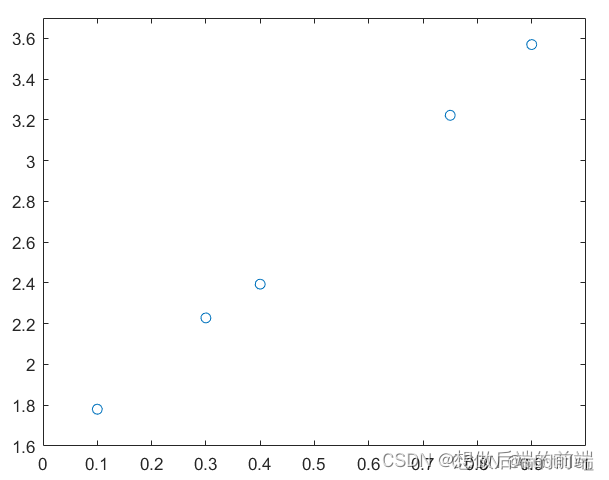
可以看出满足很好的线性关系,下面我们用上述最小二乘法的思想求一下拟合直线的k 和b :
方法1:代数方法计算
N=length(x);
k=(sum(y.*x)-N*mean(y)*mean(x))/(sum(x.^2)-N*mean(x)^2);
b=mean(y)-k*mean(x);
x_line=linspace(0,1,101);
y_line=k*x_line+b;
plot(x_line,y_line,'Color','r','LineWidth',1)
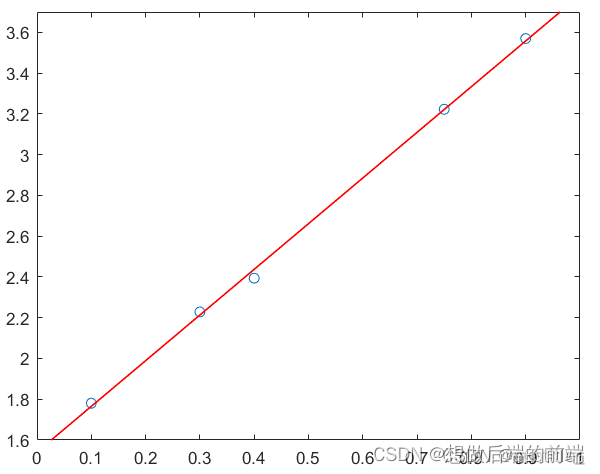
查看k和b的值:
k=2.2411
b=1.5409
方法2:矩阵计算
N=length(x);
X=[x,ones(N,1)];
Y=y;
K=inv(X'*X)*X'*Y;
k=K(1);
b=K(2);
x_line=linspace(0,1,101);
y_line=k*x_line+b;
plot(x_line,y_line,'Color','r','LineWidth',1)
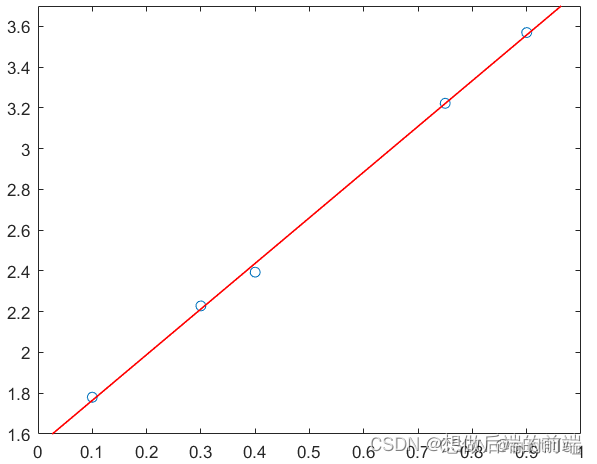
查看k和b的值:
k=2.2411
b=1.5409
至此,我们可以看到两种方法的结果是一样的。
相关文章:

线性回归与线性拟合的原理、推导与算法实现
关于回归和拟合,从它们的求解过程以及结果来看,两者似乎没有太大差别,事实也的确如此。从本质上说,回归属于数理统计问题,研究解释变量与响应变量之间的关系以及相关性等问题。而拟合是把平面的一系列点,用…...

【C++】set和multiset
文章目录 关联式容器键值对一、set介绍二、set的使用multiset 关联式容器 STL中的部分容器,比如:vector、list、deque、forward_list(C11)等,这些容器统称为序列式容器,因为其底层为线性序列的数据结构,里面存储的是元…...

二十、泛型(1)
本章概要 基本概念 与 C 的比较 简单泛型 一个元组类库一个堆栈类RandomList 基本概念 普通的类和方法只能使用特定的类型:基本数据类型或类类型。如果编写的代码需要应用于多种类型,这种严苛的限制对代码的束缚就会很大。 多态是一种面向对象思想的泛…...

【Unity数据交互】游戏中常用到的Json序列化
ˊˊ 👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏࿱…...
TCP的滑动窗口和拥塞控制
目录 滑动窗口 1.发送窗口和接收窗口 2.滑动窗口的分类 停止等待协议:发送窗口大小 1, 接收窗口大小 1 后退N帧协议(GBN):发送窗口大小 > 1,接收窗口大小 1 选择重传协议(SR…...

零信任网络:一种全新的网络安全架构
随着网络技术的不断发展,网络安全问题日益凸显。传统的网络安全策略往往基于信任和验证,但这种信任策略存在一定的局限性。为了解决这一问题,零信任网络作为一种全新的网络安全架构,逐渐受到人们的关注。本文将对零信任网络的概念…...

基于单片机的智能拐杖软件设计
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 技术交流认准下方 CSDN 官方提供的联系方式 文章目录 概要 一、整体设计方案2.1本设计设计原理2.1.1单片机基本介绍 二、本设计方案选择三、软件设计AD原理图:原理图…...
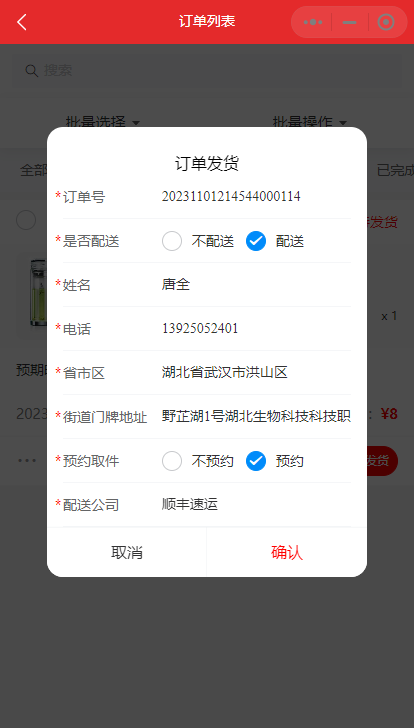
小程序如何设置自动预约快递
小程序通过设置自动预约功能,可以实现自动将订单信息发送给快递公司,快递公司可以自动上门取件。下面具体介绍如何设置。 在小程序管理员后台->配送设置处,选择首选配送公司。为了能够支持自动预约快递,请选择正常的快递公司&…...
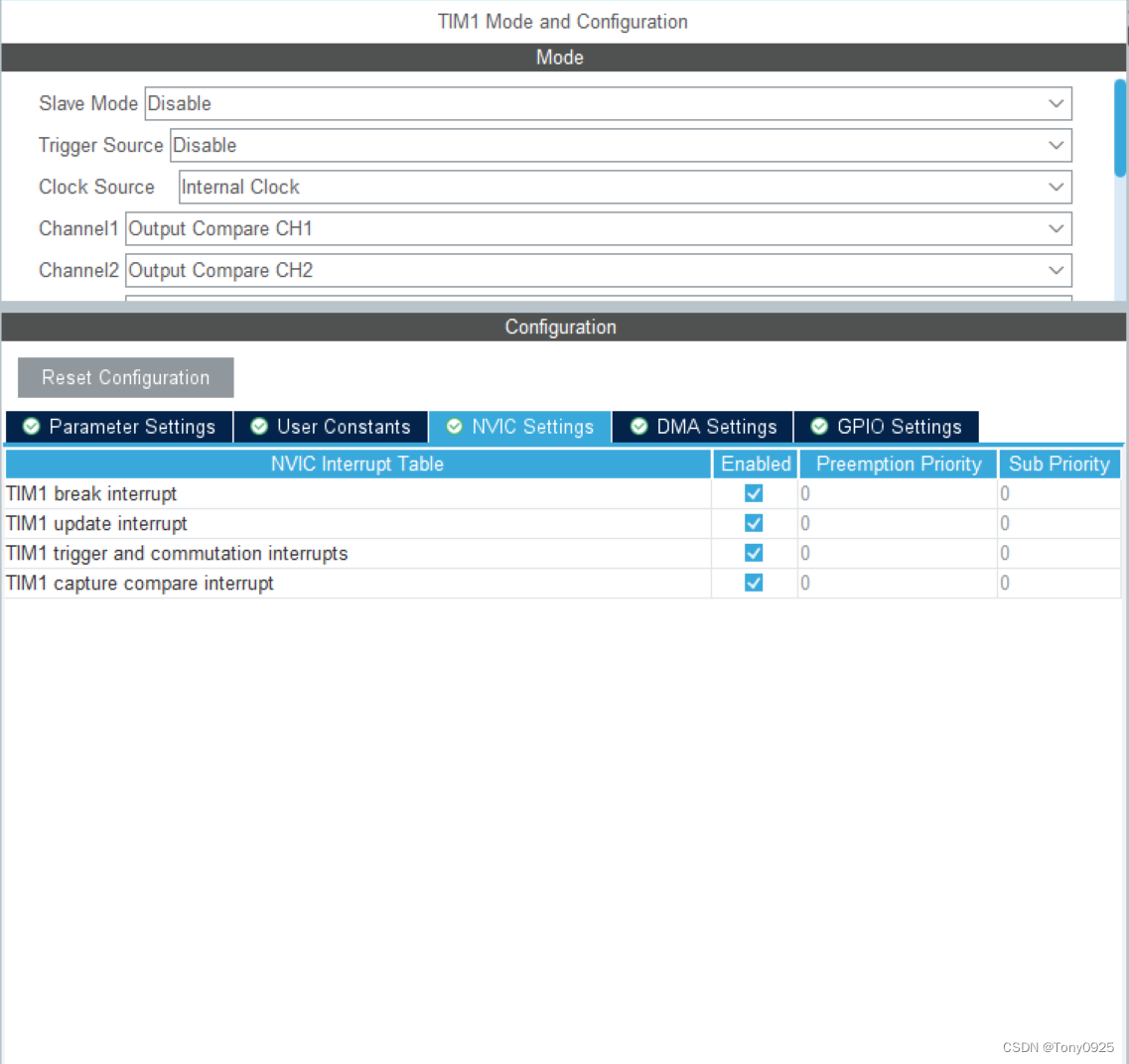
STM32-HAL库08-TIM的输出比较模式(输出PWM的另一种方式)
STM32-HAL库08-TIM的输出比较模式(输出PWM的另一种方式) 一、所用材料: STM32F103C6T6最小系统板 STM32CUBEMX(HAL库软件) MDK5 示波器或者逻辑分析仪 二、所学内容: 通过定时器TIM的输出比较模式得到预…...
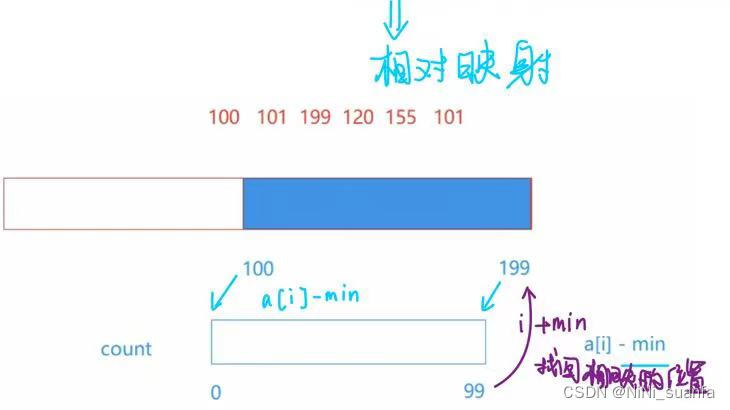
【数据结构】深入浅出讲解计数排序【图文详解,搞懂计数排序这一篇就够了】
计数排序 前言一、计数排序算法核心思路映射 概念补充绝对映射相对映射 二、计数排序算法核心实现步骤三、码源详解四、效率分析(1)时间复杂度 — O(Max(N,range))(2)空间…...

Canvas制作喷泉效果示例
Canvas能制作出很多动画效果,下面是一个制作喷泉效果的示例 效果图 源代码 <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <meta name"viewport" content"widthdevice-width, initial-scale1 ,user-…...

什么是NPM(Node Package Manager)?它的作用是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...
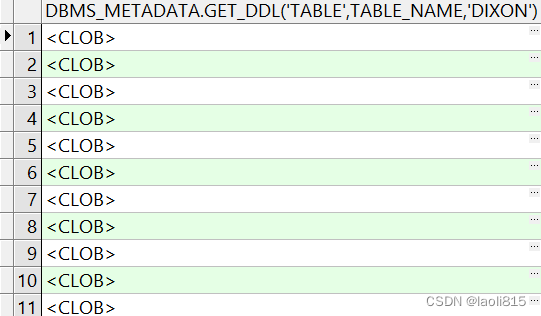
oracle如果不适用toad或者plsql工具如何获取索引建表语句
select dbms_lob.substr(dbms_metadata.get_ddl(INDEX,INDEX_NAME,DIXON))||; from dba_indexes where ownerDIXON这个语句可以获取dixon用户的所有索引创建语句,sql脚本形式呈现 点开一个语句查看 如果不使用dbms_lob.substr这个函数最后得到是一个clob selec…...
某大厂伺服驱动器量产方案
本文介一款大厂量产伺服驱动器方案!带2500线省线式编码器,17位增量编码器,20位绝对值编码器!标配CANopen、高精度运动控制,高速总线通讯,主芯片28335FPGA,已验证过,带can和485通讯&a…...
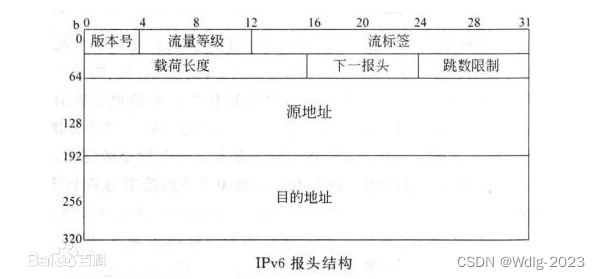
【计算机网络】网络层:数据平面
一.网络层概述 每台路由器的数据平面的主要功能时从其输入链路向其输出链路转发数据报,控制平面的主要功能是协调这些本地的每路由转发动作,使得数据报沿着源和目的地主机之间的路由器路径最终进行端到端传送。 网络层不运行运输层和应用层协议。 转发是…...
Path with “WEB-INF“ or “META-INF“: [webapp/WEB-INF/NewFile.html]
2023-11-04 01:03:14.523 WARN 10896 --- [nio-8072-exec-6] o.s.w.s.r.ResourceHttpRequestHandler : Path with "WEB-INF" or "META-INF": [webapp/WEB-INFNewFile.html] spring.mvc.view.prefix:/webapp/WEB-INF/...

百度OCR 接口调用 提示 216101:param image not exist 问题解决
百度提供的文档并没有描述如何解决,例子也是,用工具请求可以通 axios 请求 需要用FormData 传参 let token await getAccessToken() //官网案例那个 请求token// console.log(token, "token");var formData new FormData();// imageBase64 :Base64 图片数据formD…...

1-10 HTML中input属性
HTML中input属性 text:用于接受单行文本输入password:用于密码输入,输入字符会被掩盖radio:用于单选按钮,用户可以在一组选项中选择一个checkbox:用于复选框,用户可以选择多个选项number&#…...
共焦显微镜使用
x.1 细胞培养 x.2 样品制备 以细菌为例,我们使用荧光染色细菌,静置15分钟。 15分钟后我们使用实验室的专用培养皿,选择吸收100uL的溶液滴在在培养皿中心。 x.3 显微镜使用 我们按照1, 2, 3, 4的顺序打开显微镜, 打开电脑&…...
windows + Mingw32-make 编译 PoDoFo库,openssl, libjpeg, Msys2工具的使用
参考: https://blog.csdn.net/sspdfn/article/details/104244306 https://blog.csdn.net/yaoyuanyylyy/article/details/17436303 https://blog.csdn.net/wxlfreewind/article/details/106492253 前期进行了各种摸索,由于Podofo依赖库比较多,…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
