统计学习方法 牛顿法和拟牛顿法
文章目录
- 统计学习方法 牛顿法和拟牛顿法
- 牛顿法
- 拟牛顿法
- DFP 算法
- BFGS 算法
- Broyden 类算法
统计学习方法 牛顿法和拟牛顿法
学习李航的《统计学习方法》时,关于牛顿法和拟牛顿法的笔记。
牛顿法(Newton method)和拟牛顿法(quasi-Newton method)时求解无约束优化问题的常用方法,有收敛速度快的优点。牛顿法时迭代算法,每一步需要求解目标函数的 Hession 矩阵的逆矩阵,计算较为复杂;拟牛顿法通过正定矩阵近似 Hession 矩阵或其逆矩阵,简化了计算过程。
牛顿法
牛顿法的推导:考虑无约束最优化问题:
min x ∈ R n f ( x ) \min\limits_{x\in \R^n} f(x) x∈Rnminf(x)
设 x ∗ x^\ast x∗ 是目标函数的极小点。
假设 f ( x ) f(x) f(x) 具有二姐连续偏导数,若第 k k k 次迭代的值为 x ( k ) x^{(k)} x(k) ,则对 f ( x ) f(x) f(x) 在 x ( k ) x^{(k)} x(k) 附近二阶泰勒展开:
f ( x ) = f ( x ( k ) ) + g k T ( x − x ( k ) ) + 1 2 ( x − x ( k ) ) H k ( x − x ( k ) ) f(x)=f(x^{(k)})+g_k^\mathrm{T}(x-x^{(k)})+\frac{1}{2}(x-x^{(k)})H_k(x-x^{(k)}) f(x)=f(x(k))+gkT(x−x(k))+21(x−x(k))Hk(x−x(k))
其中 g k g_k gk 为 f ( x ) f(x) f(x) 在 x ( k ) x^{(k)} x(k) 处的梯度向量, H k H_k Hk 为 f ( x ) f(x) f(x) 的 Hession 矩阵在 x ( k ) x^{(k)} x(k) 处的值:
g ( x ) = ∇ f ( x ) = [ ∂ f ∂ x i ] n × 1 , H ( x ) = [ ∂ 2 f ∂ x i ∂ x j ] n × n g(x)=\nabla f(x)=\left[\frac{\partial f}{\partial x_i}\right]_{n\times 1},\quad H(x)=\left[ \frac{\partial^2 f}{\partial x_i\partial x_j} \right]_{n\times n} g(x)=∇f(x)=[∂xi∂f]n×1,H(x)=[∂xi∂xj∂2f]n×n
函数 f ( x ) f(x) f(x) 有极值的必要条件是在极值点处一阶导数(即梯度向量)为 0 0 0 。特别地,当 H ( x ) H(x) H(x) 在极值点处是正定矩阵时,函数 f ( x ) f(x) f(x) 的极值为极小值。
牛顿法利用极小点的必要条件,每次从上一次迭代得到的极小点 x ( k ) x^{(k)} x(k) 开始,得到当前目标函数的极小点 x ( k + 1 ) x^{(k+1)} x(k+1) ,即:
∇ f ( x ( k + 1 ) ) = g k + ( x ( k + 1 ) − x ( k ) ) = 0 \nabla f(x^{(k+1)})=g_k+(x^{(k+1)}-x^{(k)})=0 ∇f(x(k+1))=gk+(x(k+1)−x(k))=0
解得:
x ( k + 1 ) = x ( k ) − H k − 1 g k x^{(k+1)}=x^{(k)}-H_k^{-1}g_k x(k+1)=x(k)−Hk−1gk
假设 p k p_k pk 为一 n × 1 n\times 1 n×1 的列向量,且满足:
H k p k = − g k H_kp_k=-g_k Hkpk=−gk
则迭代公式可写为:
x ( k + 1 ) = x ( k ) + p k x^{(k+1)}=x^{(k)}+p_k x(k+1)=x(k)+pk
算法:牛顿法
- 输入:目标函数 f ( x ) f(x) f(x) ,梯度 g ( x ) = ∇ f ( x ) g(x)=\nabla f(x) g(x)=∇f(x) ,Hession 矩阵 H ( x ) H(x) H(x) ,精度 ε \varepsilon ε ;
- 输出: f ( x ) f(x) f(x) 的极小值点 x ∗ x^\ast x∗ ;
- 取初始点 x ( 0 ) x^{(0)} x(0) ,置 k = 0 k=0 k=0 ;
- 计算 g k = g ( x ( k ) ) g_k=g(x^{(k)}) gk=g(x(k)) ;
- 若 ∥ g k ∥ < ε \|g_k\|\lt \varepsilon ∥gk∥<ε ,则停止计算,返回近似解 x ∗ = x ( k ) x^\ast=x^{(k)} x∗=x(k) ;
- 计算 H k = H ( x ( k ) ) H_k=H(x^{(k)}) Hk=H(x(k)) ,并求 p k p_k pk :
H k p k = − g k H_kp_k=-g_k Hkpk=−gk
- 更新 x ( k + 1 ) = x ( k ) + p k x^{(k+1)}=x^{(k)}+p_k x(k+1)=x(k)+pk , k = k + 1 k=k+1 k=k+1 ,跳转至 2;
拟牛顿法
牛顿法中需要计算 H k − 1 H_k^{-1} Hk−1 ,比较耗时,我们考虑使用一个与 Hession 矩阵具有类似性质的 n n n 阶矩阵 G k = G ( x ( k ) ) G_k=G(x^{(k)}) Gk=G(x(k)) 来近似代替 H k − 1 H_k^{-1} Hk−1 。
条件一:首先,对 x ( k ) x^{(k)} x(k) 处的二阶泰勒展开进行求导,取 x = ( k + 1 ) x=^{(k+1)} x=(k+1) ,得:
g k + 1 − g k = H k ( x ( k + 1 ) − x ( k ) ) g_{k+1}-g_k=H_k(x^{(k+1)}-x^{(k)}) gk+1−gk=Hk(x(k+1)−x(k))
记 y k = g k + 1 − g k y_k=g_{k+1}-g_k yk=gk+1−gk , δ k = x ( k + 1 ) − x ( k ) \delta_{k}=x^{(k+1)}-x^{(k)} δk=x(k+1)−x(k) ,则满足:
y k = H k δ k y_k=H_k\delta_k yk=Hkδk
或:
H k − 1 y k = δ k H_k^{-1}y_k=\delta_k Hk−1yk=δk
该条件称为拟牛顿条件。
条件二:如果 H k H_k Hk 是正定的( H k − 1 H_k^{-1} Hk−1 也是正定的),那么可以保证牛顿法搜索方向 p k p_k pk 是下降方向,因为:
x ( k + 1 ) = x ( k ) + λ p k = x ( k ) − λ H k − 1 g k x^{(k+1)}=x^{(k)}+\lambda p_k=x^{(k)}-\lambda H_k^{-1}g_k x(k+1)=x(k)+λpk=x(k)−λHk−1gk
带入前面的泰勒展开式,为:
f ( x ( k + 1 ) ) = f ( x k ) − λ g k T H k − 1 g k + 1 2 λ 2 g k T H k − T H k H k − 1 g k ≈ f ( x k ) − λ g k T H k − 1 g k f(x^{(k+1)})=f(x^{k})-\lambda g_k^{\mathrm{T}}H_k^{-1}g_k+\frac{1}{2}\lambda^2g_k^\mathrm{T}H_k^{-\mathrm{T}}H_kH_{k}^{-1}g_k\approx f(x^{k})-\lambda g_k^{\mathrm{T}}H_k^{-1}g_k f(x(k+1))=f(xk)−λgkTHk−1gk+21λ2gkTHk−THkHk−1gk≈f(xk)−λgkTHk−1gk
当 λ \lambda λ 为一个足够小的正数时,由于 H k H_k Hk 正定,即 λ g k T H k − 1 g k > 0 \lambda g_k^{\mathrm{T}}H_k^{-1}g_k \gt 0 λgkTHk−1gk>0 ,因此有 f ( x ( k + 1 ) ) < f ( x ( k ) ) f(x^{(k+1)})\lt f(x^{(k)}) f(x(k+1))<f(x(k)) ,也就是说 p k p_k pk 时下降方向。
综合前面两个条件,我们在选择近似矩阵 G k G_k Gk 时,首先要求每次迭代时 G k G_k Gk 是正定的,其次 G k G_k Gk 需要满足以下的拟牛顿条件:
G k + 1 y k = δ k G_{k+1}y_{k}=\delta_k Gk+1yk=δk
同时,按照拟牛顿条件,每次迭代可以选择更新矩阵 G k + 1 G_{k+1} Gk+1 :
G k + 1 = G k + Δ G k G_{k+1}=G_{k}+\Delta G_{k} Gk+1=Gk+ΔGk
有多种选择近似矩阵的方法:
DFP 算法
DFP (Davidon-Fletcher-Powell)算法对 G k G_{k} Gk 的更新为:
G k + 1 = G k + P k + Q k G_{k+1}=G_{k}+P_k+Q_k Gk+1=Gk+Pk+Qk
其中 P k P_k Pk 和 Q k Q_k Qk 是待定矩阵,此时:
G k + 1 y k = G k y k + P k y k + Q k y k = δ k G_{k+1}y_{k}=G_ky_k+P_ky_k+Q_ky_k=\delta_k Gk+1yk=Gkyk+Pkyk+Qkyk=δk
为了满足拟牛顿条件,可以令:
P k y k = δ k , Q k y k = − G k y k P_ky_k=\delta_k,\quad Q_ky_k=-G_ky_k Pkyk=δk,Qkyk=−Gkyk
书上给了一个例子:
P k = δ k δ k T δ k T y k , Q k = − G k y k y k T G k y k T G k y k P_k=\frac{\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k},\quad Q_k=-\frac{G_ky_ky_k^{\mathrm{T}}G_k}{y_k^{\mathrm{T}}G_ky_k} Pk=δkTykδkδkT,Qk=−ykTGkykGkykykTGk
可以证明(咱也不知道怎么证明),如果 G 0 G_0 G0 是正定的,则迭代过程中的每个矩阵 G k G_k Gk 都是正定的。
算法:DFP 算法
- 输入:目标函数 f ( x ) f(x) f(x) ,梯度 g ( x ) = ∇ f ( x ) g(x)=\nabla f(x) g(x)=∇f(x) ,精度 ε \varepsilon ε ;
- 输出: f ( x ) f(x) f(x) 的极小点 x ∗ x^\ast x∗ ;
- 选定初始点 x ( 0 ) x^{(0)} x(0) ,取 G 0 G_0 G0 为正定对称矩阵,置 k = 0 k=0 k=0 ;
- 计算 g k = g ( x ( k ) ) g_k=g(x^{(k)}) gk=g(x(k)) ,若 ∥ g ( x ( k ) ) ∥ < ε \|g(x^{(k)})\| \lt \varepsilon ∥g(x(k))∥<ε ,则停止计算,返回近似解 x ∗ = x ( k ) x^\ast=x^{(k)} x∗=x(k) ,否则继续;
- 计算 p k = − G k g k p_k=-G_kg_k pk=−Gkgk ;
- 一维搜索:求 λ k \lambda_k λk 使得:
f ( x ( k ) + λ k p k ) = min λ ≥ 0 f ( x ( k ) + λ p k ) f(x^{(k)}+\lambda_kp_k)=\min_{\lambda \geq 0}f(x^{(k)}+\lambda p_k) f(x(k)+λkpk)=λ≥0minf(x(k)+λpk)
- 置 x ( k + 1 ) = x ( k ) + λ k p k x^{(k+1)}=x^{(k)}+\lambda_kp_k x(k+1)=x(k)+λkpk ;
- 计算 G k + 1 G_{k+1} Gk+1 ,置 k = k + 1 k=k+1 k=k+1 ,转 2;
G k + 1 = G k + δ k δ k T δ k T y k − G k y k y k T G k y k T G k y k G_{k+1}=G_{k}+\frac{\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k}-\frac{G_ky_ky_k^{\mathrm{T}}G_k}{y_k^{\mathrm{T}}G_ky_k} Gk+1=Gk+δkTykδkδkT−ykTGkykGkykykTGk
BFGS 算法
BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法是最流行的拟牛顿算法。此时考虑使用 B k B_k Bk 近似 H k H_k Hk ,更新方法类似:
B k + 1 = B k + P k + Q k B_{k+1}=B_{k}+P_{k}+Q_{k} Bk+1=Bk+Pk+Qk
为了满足拟牛顿条件:
B k + 1 δ k = B k δ k + P k δ k + Q k δ k = y k B_{k+1}\delta_k=B_k\delta_k+P_k\delta_k+Q_k\delta_k=y_k Bk+1δk=Bkδk+Pkδk+Qkδk=yk
取:
P k δ k = y k , Q k δ k = − B k δ k P_k\delta_k=y_k,\quad Q_k\delta_k=-B_k\delta_k Pkδk=yk,Qkδk=−Bkδk
同样可令:
P k = y k y k T y k T δ k , Q k = − B k δ k δ k T B k δ k T B k δ k P_k=\frac{y_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k},\quad Q_k=-\frac{B_k\delta_k\delta_k^{\mathrm{T}}B_k}{\delta_k^{\mathrm{T}}B_k\delta_k} Pk=ykTδkykykT,Qk=−δkTBkδkBkδkδkTBk
算法:BFGS 算法
- 输入:目标函数 f ( x ) f(x) f(x) ,梯度 g ( x ) = ∇ f ( x ) g(x)=\nabla f(x) g(x)=∇f(x) ,精度 ε \varepsilon ε ;
- 输出: f ( x ) f(x) f(x) 的极小点 x ∗ x^\ast x∗ ;
- 选定初始点 x ( 0 ) x^{(0)} x(0) ,取 B 0 B_0 B0 为正定对称矩阵,置 k = 0 k=0 k=0 ;
- 计算 g k = g ( x ( k ) ) g_k=g(x^{(k)}) gk=g(x(k)) ,若 ∥ g ( x ( k ) ) ∥ < ε \|g(x^{(k)})\| \lt \varepsilon ∥g(x(k))∥<ε ,则停止计算,返回近似解 x ∗ = x ( k ) x^\ast=x^{(k)} x∗=x(k) ,否则继续;
- 由 B k p k = − g k B_kp_k=-g_k Bkpk=−gk 计算 p k p_k pk;
- 一维搜索:求 λ k \lambda_k λk 使得:
f ( x ( k ) + λ k p k ) = min λ ≥ 0 f ( x ( k ) + λ p k ) f(x^{(k)}+\lambda_kp_k)=\min_{\lambda \geq 0}f(x^{(k)}+\lambda p_k) f(x(k)+λkpk)=λ≥0minf(x(k)+λpk)
- 置 x ( k + 1 ) = x ( k ) + λ k p k x^{(k+1)}=x^{(k)}+\lambda_kp_k x(k+1)=x(k)+λkpk ;
- 计算 B k + 1 B_{k+1} Bk+1 ,置 k = k + 1 k=k+1 k=k+1 ,转 2;
B k + 1 = B k + y k y k T y k T δ k − B k δ k δ k T B k δ k T B k δ k B_{k+1}=B_{k}+\frac{y_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}-\frac{B_k\delta_k\delta_k^{\mathrm{T}}B_k}{\delta_k^{\mathrm{T}}B_k\delta_k} Bk+1=Bk+ykTδkykykT−δkTBkδkBkδkδkTBk
Broyden 类算法
根据 BFGS 算法中 B k B_k Bk 矩阵的迭代公式,我们可以得到对应的 G k G_k Gk 矩阵。有 G k = B k − 1 G_k=B_k^{-1} Gk=Bk−1 , G k + 1 − 1 = B k + 1 − 1 G_{k+1}^{-1}=B_{k+1}^{-1} Gk+1−1=Bk+1−1 ;有:
G k + 1 − 1 = G k − 1 + y k y k T y k T δ k − G k − 1 δ k δ k T G k − 1 δ k T G k − 1 δ k ⇒ G k + 1 = ( G k − 1 + y k y k T y k T δ k + − G k − 1 δ k δ k T G k − 1 δ k T G k − 1 δ k ) − 1 \begin{aligned} G_{k+1}^{-1}=&\, G_{k}^{-1}+\frac{y_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}-\frac{G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}}{\delta_k^{\mathrm{T}}G_k^{-1}\delta_k} \\ \Rightarrow G_{k+1}=&\, \left( G_{k}^{-1}+\frac{y_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}+\frac{-G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}}{\delta_k^{\mathrm{T}}G_k^{-1}\delta_k} \right)^{-1} \\ \end{aligned} Gk+1−1=⇒Gk+1=Gk−1+ykTδkykykT−δkTGk−1δkGk−1δkδkTGk−1(Gk−1+ykTδkykykT+δkTGk−1δk−Gk−1δkδkTGk−1)−1
需要用到 Shermax-Morrison 公式:
( A + u v T ) − 1 = A − 1 − A − 1 u v T A − 1 1 + v T A − 1 u (A+uv^\mathrm{T})^{-1}=A^{-1}-\frac{A^{-1}uv^\mathrm{T}A^{-1}}{1+v^{\mathrm{T}}A^{-1}u} (A+uvT)−1=A−1−1+vTA−1uA−1uvTA−1
其中 u u u 和 v v v 为 n n n 维向量, A A A 为可逆矩阵;记:
A = G k − 1 + y k y k T y k T δ k , u = − G k − 1 δ k , v T = δ k T G k − 1 δ k T G k − 1 δ k A=G_k^{-1}+\frac{y_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k},\quad u=-G_k^{-1}\delta_k,\quad v^{\mathrm{T}}=\frac{\delta_k^{\mathrm{T}}G_k^{-1}}{\delta_k^{\mathrm{T}}G_k^{-1}\delta_k} A=Gk−1+ykTδkykykT,u=−Gk−1δk,vT=δkTGk−1δkδkTGk−1
则:
G k + 1 = ( A + − G k − 1 δ k δ k T G k − 1 δ k T G k − 1 δ k ) − 1 = A − 1 + A − 1 G k − 1 δ k δ k T G k − 1 δ k T G k − 1 δ k A − 1 1 − δ k T G k − 1 A − 1 G k − 1 δ k δ k T G k − 1 δ k = A − 1 + A − 1 G k − 1 δ k δ k T G k − 1 A − 1 δ k T G k − 1 δ k − δ k T G k − 1 A − 1 G k − 1 δ k \begin{aligned} G_{k+1} =&\, \left(A+\frac{-G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}}{\delta_k^{\mathrm{T}}G_k^{-1}\delta_k}\right)^{-1} \\ =&\, A^{-1}+\frac{A^{-1}\frac{G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}}{\delta_k^{\mathrm{T}}G_k^{-1}\delta_k}A^{-1}}{1-\frac{\delta_k^{\mathrm{T}}G_k^{-1}A^{-1}G_k^{-1}\delta_{k}} {\delta_k^{\mathrm{T}}G_k^{-1}\delta_k}} \\ =&\, A^{-1}+\frac{A^{-1}G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}A^{-1}}{\delta_k^{\mathrm{T}}G_k^{-1}\delta_k-\delta_k^{\mathrm{T}}G_k^{-1}A^{-1}G_k^{-1}\delta_{k}} \end{aligned} Gk+1===(A+δkTGk−1δk−Gk−1δkδkTGk−1)−1A−1+1−δkTGk−1δkδkTGk−1A−1Gk−1δkA−1δkTGk−1δkGk−1δkδkTGk−1A−1A−1+δkTGk−1δk−δkTGk−1A−1Gk−1δkA−1Gk−1δkδkTGk−1A−1
对 A A A 再次使用公式,此时 u = y k u=y_k u=yk , v T = y k T y k T δ k v^{\mathrm{T}}=\frac{y_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k} vT=ykTδkykT ,得到:
A − 1 = ( G k − 1 + y k y k T y k T δ k ) − 1 = G k − G k y k y k T y k T δ k G k 1 + y k T G k y k y k T δ k = G k − G k y k y k T G k y k T δ k + y k T G k y k A^{-1}=\left(G_k^{-1}+\frac{y_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}\right)^{-1} =G_{k}-\frac{G_k\frac{y_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}G_k} {1+\frac{y_k^{\mathrm{T}}G_ky_k}{y_k^{\mathrm{T}}\delta_k}} =G_{k}-\frac{G_ky_ky_k^{\mathrm{T}}G_k} {y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k} A−1=(Gk−1+ykTδkykykT)−1=Gk−1+ykTδkykTGkykGkykTδkykykTGk=Gk−ykTδk+ykTGkykGkykykTGk
将 A − 1 A^{-1} A−1 逐步代入 G k + 1 G_{k+1} Gk+1 ,得到:
G k + 1 = A − 1 + A − 1 G k − 1 δ k δ k T G k − 1 A − 1 δ k T G k − 1 δ k − δ k T G k − 1 A − 1 G k − 1 δ k = A − 1 + A − 1 G k − 1 δ k δ k T G k − 1 A − 1 δ k T G k − 1 δ k − δ k T G k − 1 ( G k − G k y k y k T G k y k T δ k + y k T G k y k ) G k − 1 δ k = A − 1 + A − 1 G k − 1 δ k δ k T G k − 1 A − 1 δ k T y k y k T δ k y k T δ k + y k T G k y k = A − 1 + ( G k − G k y k y k T G k y k T δ k + y k T G k y k ) ( G k − 1 δ k δ k T G k − 1 δ k T y k y k T δ k y k T δ k + y k T G k y k ) ( G k − G k y k y k T G k y k T δ k + y k T G k y k ) = A − 1 + ( I − G k y k y k T y k T δ k + y k T G k y k ) ( δ k δ k T δ k T y k y k T δ k y k T δ k + y k T G k y k ) ( I − y k y k T G k y k T δ k + y k T G k y k ) = A − 1 + ( ( δ k δ k T ) ( y k T δ k + y k T G k y k ) δ k T y k y k T δ k ) − ( δ k δ k T y k y k T G k δ k T y k y k T δ k ) − ( G k y k y k T δ k δ k T δ k T y k y k T δ k ) + ( G k y k y k T δ k δ k T y k y k T G k ( δ k T y k y k T δ k ) ( y k T δ k + y k T G k y k ) ) = G k − G k y k y k T G k y k T δ k + y k T G k y k + ( ( δ k δ k T ) ( y k T δ k + y k T G k y k ) δ k T y k y k T δ k ) − ( δ k δ k T y k y k T G k δ k T y k y k T δ k ) − ( G k y k y k T δ k δ k T δ k T y k y k T δ k ) + ( G k y k y k T G k y k T δ k + y k T G k y k ) = G k + ( ( δ k δ k T ) ( y k T δ k ) δ k T y k y k T δ k ) + ( ( δ k δ k T ) ( y k T G k y k ) δ k T y k y k T δ k ) − ( δ k y k T G k y k T δ k ) − ( G k y k δ k T δ k T y k ) = G k − ( G k y k δ k T δ k T y k ) − ( δ k y k T G k y k T δ k ) + ( δ k ( y k T G k y k ) δ k T δ k T y k y k T δ k ) + ( δ k δ k T δ k T y k ) = G k ( I − y k δ k T δ k T y k ) − ( δ k y k T G k y k T δ k ) ( I − y k δ k T δ k T y k ) + ( δ k δ k T δ k T y k ) = ( I − δ k y k T y k T δ k ) G k ( I − y k δ k T δ k T y k ) + ( δ k δ k T δ k T y k ) = ( I − δ k y k T y k T δ k ) G k ( I − δ k y k T y k T δ k ) T + ( δ k δ k T δ k T y k ) \begin{aligned} G_{k+1} =&\, A^{-1}+\frac{A^{-1}G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}A^{-1}}{\delta_k^{\mathrm{T}}G_k^{-1}\delta_k-\delta_k^{\mathrm{T}}G_k^{-1}A^{-1}G_k^{-1}\delta_{k}} \\ =&\, A^{-1}+\frac{A^{-1}G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}A^{-1}}{\delta_k^{\mathrm{T}}G_k^{-1}\delta_k-\delta_k^{\mathrm{T}}G_k^{-1} \left( G_{k}-\frac{G_ky_ky_k^{\mathrm{T}}G_k} {y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k} \right) G_k^{-1}\delta_{k}} \\ =&\, A^{-1}+\frac{A^{-1}G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}A^{-1}} {\frac{\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k}{y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k}} \\ =&\, A^{-1}+ \left( G_{k}-\frac{G_ky_ky_k^{\mathrm{T}}G_k} {y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k} \right) \left( \frac{G_k^{-1}\delta_k\delta_k^{\mathrm{T}}G_k^{-1}} {\frac{\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k}{y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k}} \right) \left( G_{k}-\frac{G_ky_ky_k^{\mathrm{T}}G_k} {y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k} \right) \\ =&\, A^{-1}+ \left( I-\frac{G_ky_ky_k^{\mathrm{T}}} {y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k} \right) \left( \frac{\delta_k\delta_k^{\mathrm{T}}} {\frac{\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k}{y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k}} \right) \left( I-\frac{y_ky_k^{\mathrm{T}}G_k} {y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k} \right) \\ =&\, A^{-1}+ \left( \frac{(\delta_k\delta_k^{\mathrm{T}})(y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k)} {\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) -\left( \frac{\delta_k\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}G_k}{\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) -\left( \frac{G_ky_ky_k^{\mathrm{T}}\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) +\left( \frac{G_ky_ky_k^{\mathrm{T}}\delta_k\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}G_k} {(\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k)(y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k)} \right) \\ =&\, G_{k}-\frac{G_ky_ky_k^{\mathrm{T}}G_k} {y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k} \\ +&\,\left( \frac{(\delta_k\delta_k^{\mathrm{T}})(y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k)} {\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) -\left( \frac{\delta_k\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}G_k}{\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) -\left( \frac{G_ky_ky_k^{\mathrm{T}}\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) +\left( \frac{G_ky_ky_k^{\mathrm{T}}G_k} {y_k^{\mathrm{T}}\delta_k+y_k^{\mathrm{T}}G_ky_k} \right) \\ =&\, G_{k}+ \left( \frac{(\delta_k\delta_k^{\mathrm{T}})(y_k^{\mathrm{T}}\delta_k)} {\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) +\left( \frac{(\delta_k\delta_k^{\mathrm{T}})(y_k^{\mathrm{T}}G_ky_k)} {\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) -\left( \frac{\delta_ky_k^{\mathrm{T}}G_k}{y_k^{\mathrm{T}}\delta_k} \right) -\left( \frac{G_ky_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) \\ =&\, G_{k} -\left( \frac{G_ky_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) -\left( \frac{\delta_ky_k^{\mathrm{T}}G_k}{y_k^{\mathrm{T}}\delta_k} \right) +\left( \frac{\delta_k(y_k^{\mathrm{T}}G_ky_k)\delta_k^{\mathrm{T}}} {\delta_k^{\mathrm{T}}y_ky_k^{\mathrm{T}}\delta_k} \right) +\left( \frac{\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) \\ =&\, G_{k}\left( I- \frac{y_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) -\left( \frac{\delta_ky_k^{\mathrm{T}}G_k}{y_k^{\mathrm{T}}\delta_k} \right) \left( I-\frac{y_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) +\left( \frac{\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) \\ =&\, \left( I- \frac{\delta_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}\right) G_k \left( I-\frac{y_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) +\left( \frac{\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) \\ =&\, \left( I- \frac{\delta_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}\right) G_k \left( I- \frac{\delta_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}\right)^\mathrm{T} +\left( \frac{\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} \right) \\ \end{aligned} Gk+1=======+=====A−1+δkTGk−1δk−δkTGk−1A−1Gk−1δkA−1Gk−1δkδkTGk−1A−1A−1+δkTGk−1δk−δkTGk−1(Gk−ykTδk+ykTGkykGkykykTGk)Gk−1δkA−1Gk−1δkδkTGk−1A−1A−1+ykTδk+ykTGkykδkTykykTδkA−1Gk−1δkδkTGk−1A−1A−1+(Gk−ykTδk+ykTGkykGkykykTGk) ykTδk+ykTGkykδkTykykTδkGk−1δkδkTGk−1 (Gk−ykTδk+ykTGkykGkykykTGk)A−1+(I−ykTδk+ykTGkykGkykykT) ykTδk+ykTGkykδkTykykTδkδkδkT (I−ykTδk+ykTGkykykykTGk)A−1+(δkTykykTδk(δkδkT)(ykTδk+ykTGkyk))−(δkTykykTδkδkδkTykykTGk)−(δkTykykTδkGkykykTδkδkT)+((δkTykykTδk)(ykTδk+ykTGkyk)GkykykTδkδkTykykTGk)Gk−ykTδk+ykTGkykGkykykTGk(δkTykykTδk(δkδkT)(ykTδk+ykTGkyk))−(δkTykykTδkδkδkTykykTGk)−(δkTykykTδkGkykykTδkδkT)+(ykTδk+ykTGkykGkykykTGk)Gk+(δkTykykTδk(δkδkT)(ykTδk))+(δkTykykTδk(δkδkT)(ykTGkyk))−(ykTδkδkykTGk)−(δkTykGkykδkT)Gk−(δkTykGkykδkT)−(ykTδkδkykTGk)+(δkTykykTδkδk(ykTGkyk)δkT)+(δkTykδkδkT)Gk(I−δkTykykδkT)−(ykTδkδkykTGk)(I−δkTykykδkT)+(δkTykδkδkT)(I−ykTδkδkykT)Gk(I−δkTykykδkT)+(δkTykδkδkT)(I−ykTδkδkykT)Gk(I−ykTδkδkykT)T+(δkTykδkδkT)
因此得到 BFGS 算法的 G k G_k Gk 的迭代公式:
G k + 1 BFGS = ( I − δ k y k T y k T δ k ) G k BFGS ( I − δ k y k T y k T δ k ) T + δ k δ k T δ k T y k G_{k+1}^{\text{BFGS}}= \left( I- \frac{\delta_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}\right) G_k^{\text{BFGS}} \left( I- \frac{\delta_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}\right)^\mathrm{T} +\frac{\delta_k\delta_k^{\mathrm{T}}}{\delta_k^{\mathrm{T}}y_k} Gk+1BFGS=(I−ykTδkδkykT)GkBFGS(I−ykTδkδkykT)T+δkTykδkδkT
由 DFP 算法得到的 G k G_k Gk 记作 G k DFP G_k^{\text{DFP}} GkDFP ,可知二者的线性组合也满足拟牛顿条件式,而且是正定的:
G k + 1 = α G k DFP + ( 1 − α ) G k BFGS , 0 ≤ α ≤ 1 G_{k+1}=\alpha G_k^{\text{DFP}}+(1-\alpha)G_k^{\text{BFGS}},\quad 0\leq\alpha\leq 1 Gk+1=αGkDFP+(1−α)GkBFGS,0≤α≤1
这样就得到了一类拟牛顿算法,称为 Broyden 类算法。
相关文章:

统计学习方法 牛顿法和拟牛顿法
文章目录 统计学习方法 牛顿法和拟牛顿法牛顿法拟牛顿法DFP 算法BFGS 算法Broyden 类算法 统计学习方法 牛顿法和拟牛顿法 学习李航的《统计学习方法》时,关于牛顿法和拟牛顿法的笔记。 牛顿法(Newton method)和拟牛顿法(quasi-…...
React基础知识02
一、通过属性来传值(props) react中可以使用属性(props)可以传递给子组件,子组件可以使用这些属性值来控制其行为和呈现输出。 例子: // 1.1 父组件 import React, { useState } from react // 1.2引入子…...

Oracle(10)Managing Undo Data
目录 一、基础知识 1、AUM :Init Parameters AUM:初始化参数 2、AUM:Other Parameters AUM:其他参数 3、AUM:Sizing an UNDO TS AUM:调整UNDOTS的大小 4、AUM :Undo Quota AUM:撤消配额 5、Get Undo Segment Info 获取撤消段信息 二、基础操作 1、AUM:UNDO Tablespace …...

Xcode 14.3 新版问题总结
1. "xxx/IntermediateBuildFilesPath/UninstalledProducts/iphoneos/xxxx" failed: No such file or directory 解决:Pods/Targets Support Files/Pods-App-frameworks.sh中 if [ -L "${source}" ]; thenecho "Symlinked..."# sour…...
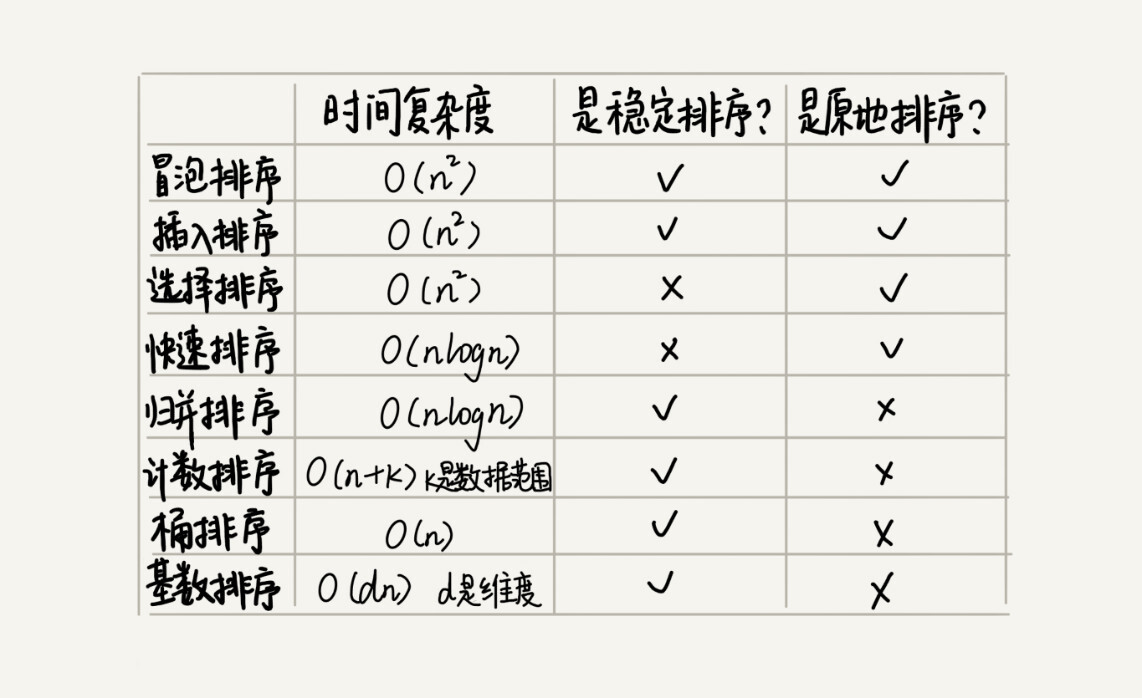
14 _ 排序优化:如何实现一个通用的、高性能的排序函数?
几乎所有的编程语言都会提供排序函数,比如C语言中qsort(),C++ STL中的sort()、stable_sort(),还有Java语言中的Collections.sort()。在平时的开发中,我们也都是直接使用这些现成的函数来实现业务逻辑中的排序功能。那你知道这些排序函数是如何实现的吗?底层都利用了哪种排…...
如何记录每天的工作日程?电脑手机通用的日程管理软件
在工作时间有限,但工作任务愈加繁多的现在职场中,要求每一个职场人士做好高效日程管理。通过高效管理日程,我们可以更好地组织和安排任务,合理分配时间和优先级,这有助于我们更专注地进行工作,减少时间的浪…...

基础Redis-结构与命令
结构与命令 1.基础-Redisa.Redis数据结构介绍b.Redis通用命令c.key的结构d.String类型e.Hash类型f.List类型g.Set类型h.SortedSet类型 1.基础-Redis a.Redis数据结构介绍 Redis是一个key-value的数据库,key一般是String类型,不过value的类型多种多样&a…...
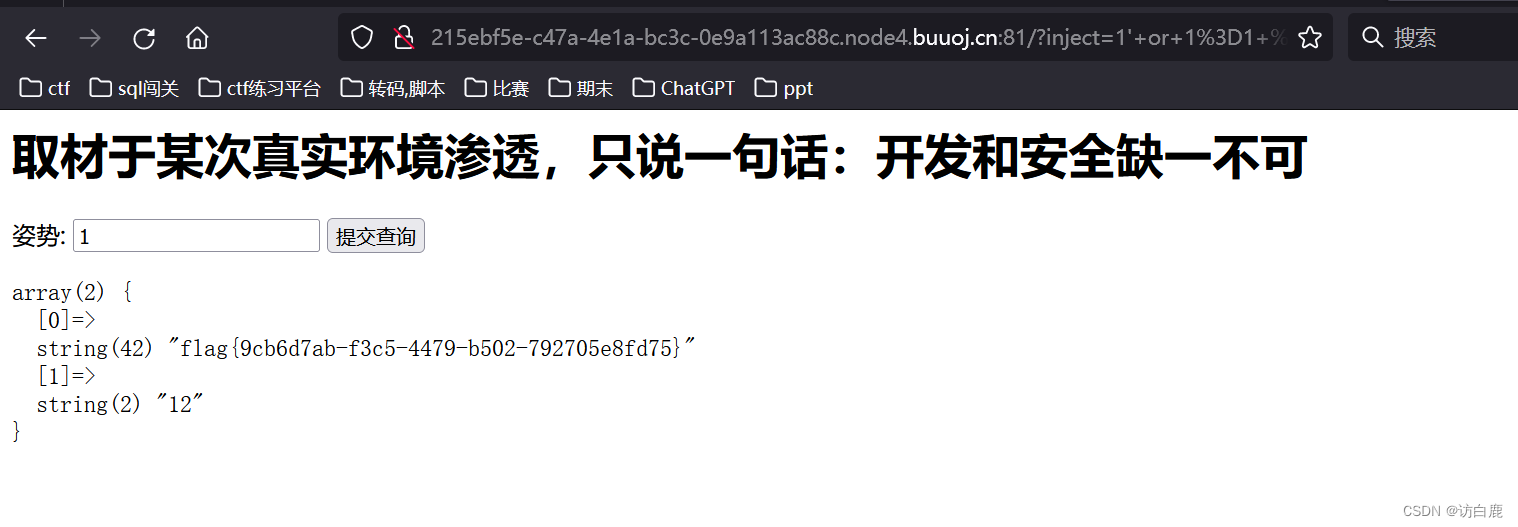
[强网杯 2019]随便注1
打开题目 输入1 输入1,页面报错,输入1 #页面正常 说明1为注入点且注入方式为字符型的单引号注入 判断列名 输入 1 order by 2 # 页面正常 1 order by 3 #页面报错 说明列名字段数为2 接下来我们尝试用联合注入的方式爆出数据显示位 输入1 union s…...
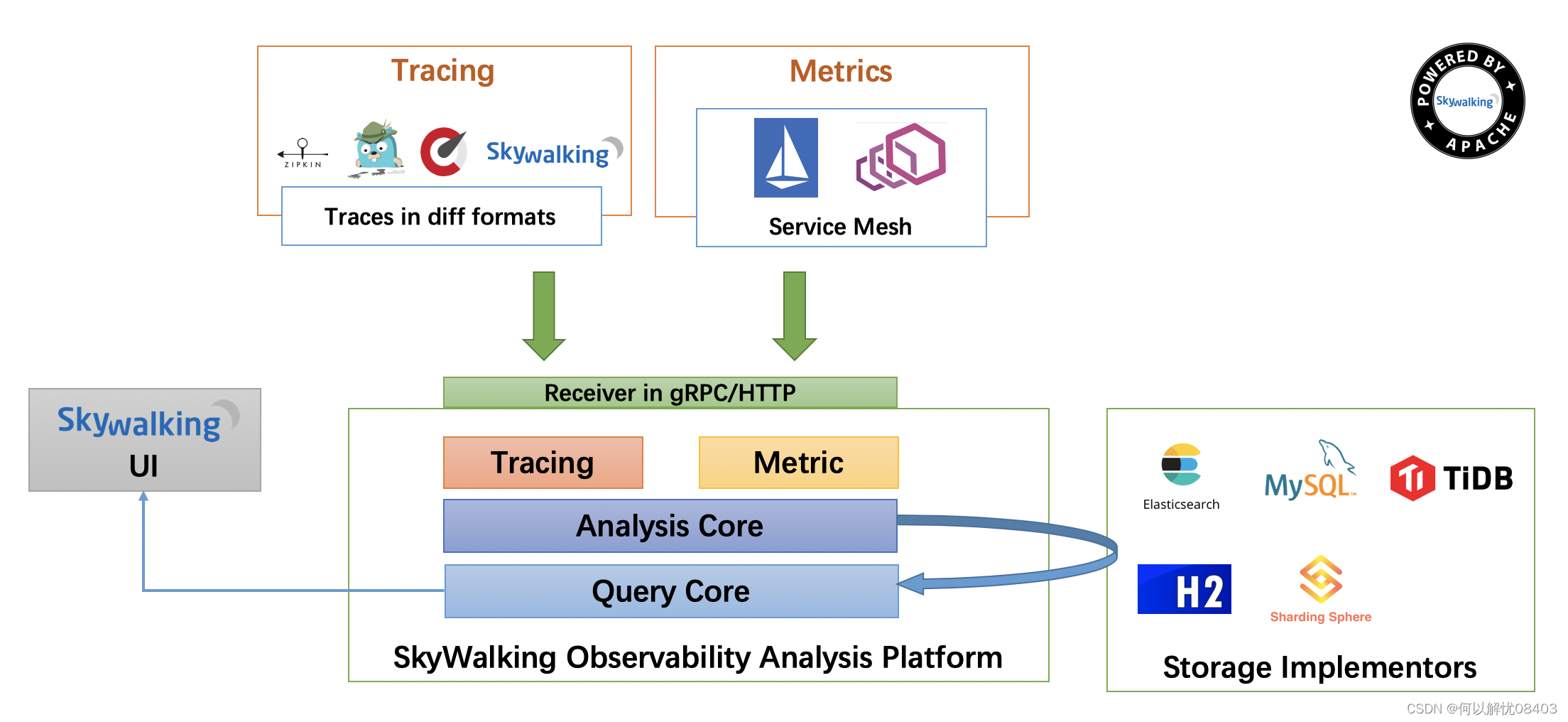
Skywalking介绍
一个优秀的项目,除了具有高拓展的架构、高性能的方案、高质量的代码之外,还应该在上线后具备多角度的监控功能。现在企业中的监控服务也有很多,Skywalking除了提供多维度、多粒度的监控之外,也提供了良好的图形化界面以及性能剖析…...
K8S知识点(四)
(1)环境搭建-集群安装 查看所需镜像 定义下载镜像 循环下载镜像: 下载完成之后:查看一下镜像,名字也已经改成了k8s的名字 集群初始化只在master节点上运行, 出现sucessfully表示成功,提示要运…...
)
Android WMS——WMS窗口更新移除(十四)
前面通过几篇的文章详细的介绍了 Window 窗口的添加过程,这里我们简单看一下,AMS 如何实现 Window 窗口的更新和移除流程。 一、窗口更新 这里我们从 Session 开始分析。 1、Session 源码位置:/frameworks/base/services/core/java/com/android/server/wm/Session.java …...

Java程序设计2023-第三次上机练习
这次的练习主要是一些类的高阶操作,像继承、接口和内部类这些,但其实还是挺简单的 目录 7-1 jmu-Java-03面向对象基础-04-形状-继承 前言 本题描述 思考 输入样例: 输出样例: 7-3 jmu-Java-04面向对象进阶-03-接口-自定义接口ArrayIntegerStack m…...
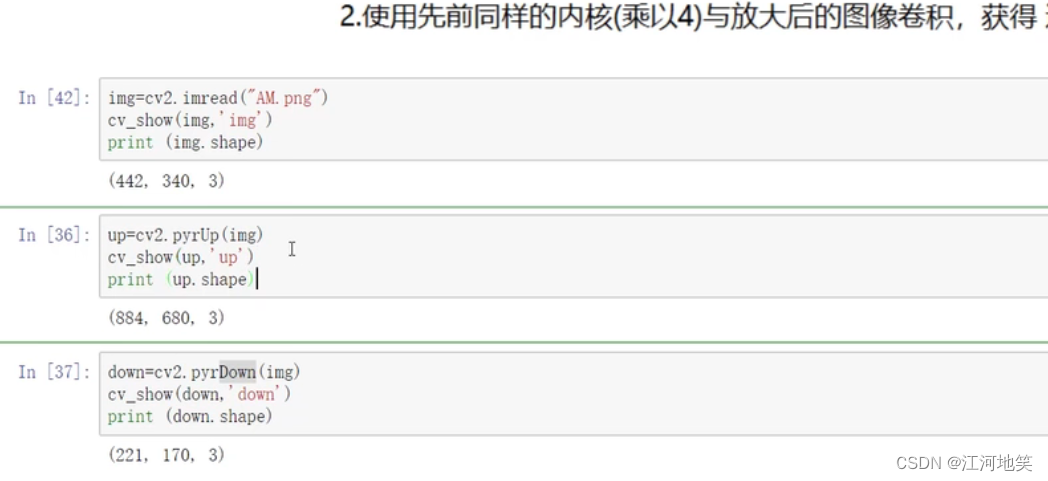
opencv复习(简短的一次印象记录)
2-高斯与中值滤波_哔哩哔哩_bilibili 1、均值滤波 2、高斯滤波 3、中值滤波 4、腐蚀操作 卷积核不都是255就腐蚀掉 5、膨胀操作 6、开运算 先腐蚀再膨胀 7、闭运算 先膨胀再腐蚀 8、礼帽 原始数据-开运算结果 9、黑帽 闭运算结果-原始数据 10、Sobel算子 左-右&#x…...

pytorch-损失函数-分类和回归区别
torch.nn 库和 torch.nn.functional库的区别 torch.nn库:这个库提供了许多预定义的层,如全连接层(Linear)、卷积层(Conv2d)等,以及一些损失函数(如MSELoss、CrossEntropyLoss等&…...
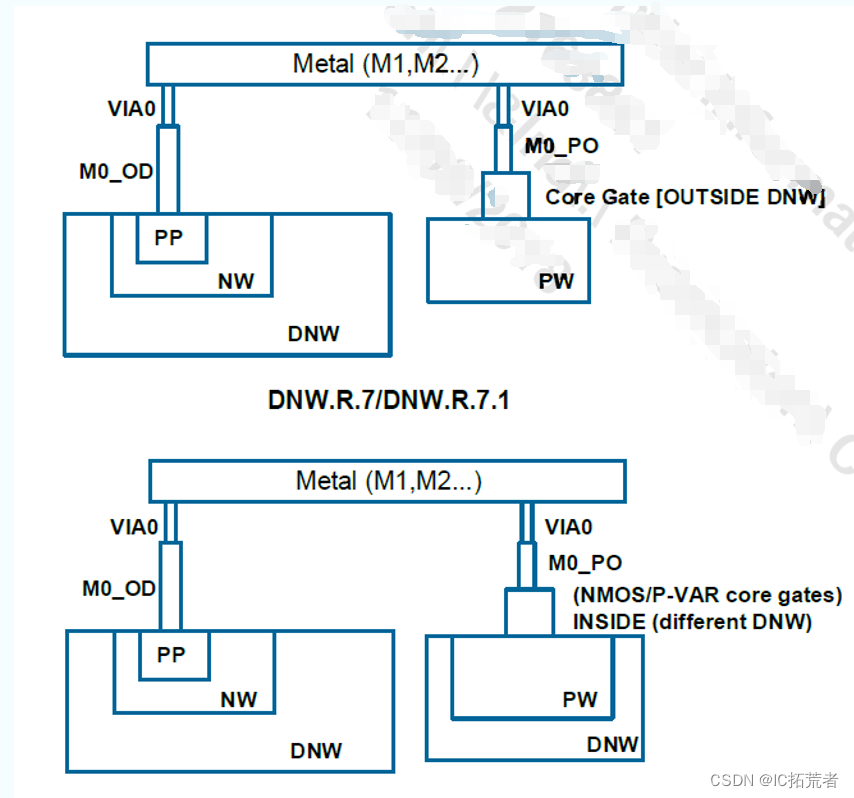
数字IC后端实现 |TSMC 12nm 与TSMC 28nm Metal Stack的区别
下图为咱们社区IC后端训练营项目用到的Metal Stack。 芯片Tapeout Review CheckList 数字IC后端零基础入门Innovus学习教程 1P代表一层poly,10M代表有10层metal,M5x表示M2-M6为一倍最小线宽宽度的金属层,2y表示M7-M8为二倍最小线宽宽度的金…...
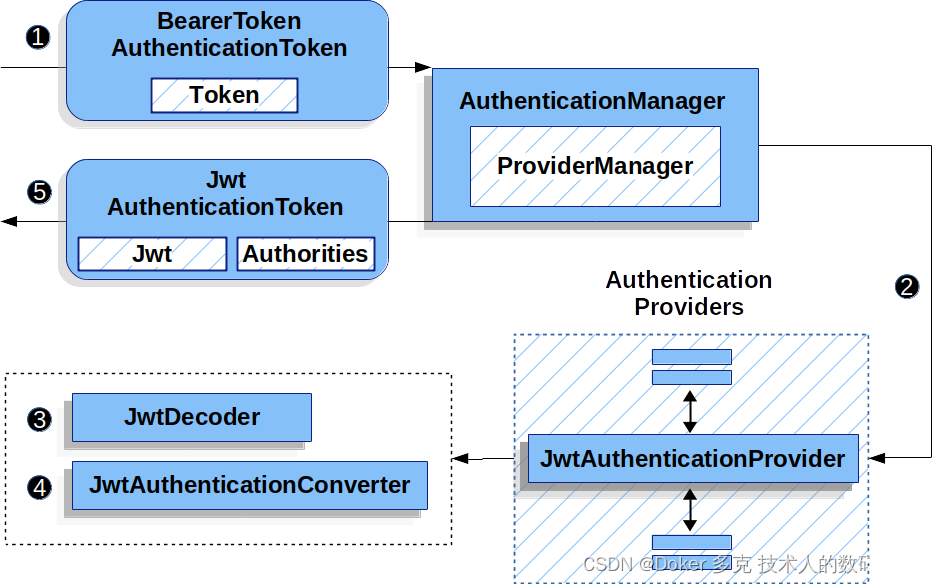
Spring Security OAuth 2.0 资源服务器— JWT
目录 一、JWT的最小依赖 二、JWT的最基本配置 1、指定授权服务器 2、初始预期(Startup Expectations) 3、运行时预期(Runtime Expectations) 三、JWT认证是如何工作的 四、直接指定授权服务器 JWK Set Uri 五、提供 audie…...

C++初阶(八)类和对象
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、Static成员1、Static概念2、Static特性3、试题 二、友元1、友元的类型2、友元函数3、 友元…...
Excel文档名称批量翻译的高效方法
在处理大量文件时,我们常常需要借助一些工具来提高工作效率。例如,在需要对Excel文档名称进行批量翻译时,一个方便快捷的工具可以帮助我们省去很多麻烦。今天,我将介绍一款名为固乔文件管家的软件,它能够帮助我们轻松实…...

python里面的浅拷贝和深拷贝
目录 浅拷贝(Shallow Copy):深拷贝(Deep Copy):实现方式:使用copy模块进行拷贝:使用切片(只适用于列表和其他序列类型)进行浅拷贝:使用list()、di…...
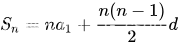
HJ76 尼科彻斯定理
题目: HJ76 尼科彻斯定理 题解: m个连续奇数之和,所以我们只要求出连续奇数的第一位就能以此枚举所有奇数,连续奇数是一个等差数列。 S m^3, n m, d 2 > a1 m^2 - (m-1) import java.util.Scanner;// 注意类名必须…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
