multiple kernel learning(MKL)多核学习
历史上之所以会出现多核学习(MKL)这个词,是因为在深度学习流行起来以前,kernel是处理非线性的默认方法,那个年代优化一个非线性函数不容易,每加一层复杂性可能就需要多设计一个优化算法,MKL就是在这种历史背景下诞生的,人们需要一个能够处理更复杂非线性,同时可靠可优化的方法,那就是用多个核,再把它们结合起来,结合的方法有很多,可以用传统的优化方法解,用一些heuristics来search参数,有的甚至不需要用参数,就是单纯地把多个kernel的结果加和起来[1]。因为这类方法在当年看来极其复杂,因此大家给了它一个特别的名字,叫做多核学习。现在回过头来,大多数MKL所定义的objectives都可以放到深度学习的框架下,一个反向传播解决了多少MKL以前想都不敢优化的问题,随着网络数越来越深,可以嵌入的核矩阵也可以做的越来越复杂,是不是还需要给他们起一个新的名字呢?不了,现在我们都叫深度学习。大家慢慢也就很少再提及MKL,以及和它一并出现过的优化算法。
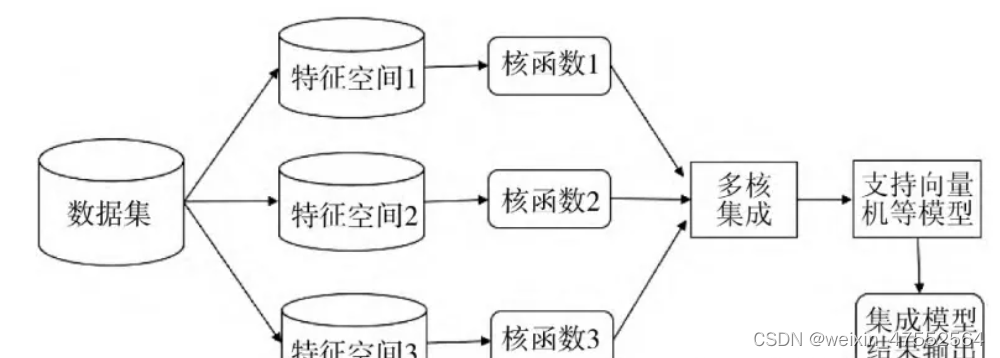
参考:https://www.cnblogs.com/XBWer/p/4492476.html
相关文章:

multiple kernel learning(MKL)多核学习
历史上之所以会出现多核学习(MKL)这个词,是因为在深度学习流行起来以前,kernel是处理非线性的默认方法,那个年代优化一个非线性函数不容易,每加一层复杂性可能就需要多设计一个优化算法,MKL就是…...

JS匿名函数之函数表达式与立即执行函数
匿名函数是什么?和具名函数有什么区别?让我为大家介绍一下吧! 没有名字的函数,无法直接使用 一.函数表达式 将匿名函数赋值给一个变量,并且通过变量名去调用,我们将这个称为函数表达式 语法: …...

WebGL:基础练习 / 简单学习 / demo / canvas3D
一、前置内容 canvas:理解canvas / 基础使用 / 实用demo-CSDN博客 WebGL:开始学习 / 理解 WebGL / WebGL 需要掌握哪些知识 / 应用领域 / 前端值得学WebGL吗_webgl培训-CSDN博客 二、在线运行HTML 用来运行WebGL代码,粘贴--运行ÿ…...

Python基础入门例程44-NP44 判断列表是否为空(条件语句)
最近的博文: Python基础入门例程43-NP43 判断布尔值(条件语句)-CSDN博客 Python基础入门例程42-NP42 公式计算器(运算符)-CSDN博客 Python基础入门例程41-NP41 二进制位运算(运算符)-CSDN博客…...

【每日一题Day369】LC187重复的DNA序列 | 字符串哈希
重复的DNA序列【LC187】 DNA序列 由一系列核苷酸组成,缩写为 A, C, G 和 T.。 例如,"ACGAATTCCG" 是一个 DNA序列 。 在研究 DNA 时,识别 DNA 中的重复序列非常有用。 给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA…...

服务器密码机主要功能及特点 安当加密
服务器密码机的主要功能包括: 数据加密:密码机使用各种加密算法对数据进行加密,确保只有拥有正确密钥的接收者才能解密和查看数据。数据解密:密码机使用相应的解密算法和密钥对已加密的数据进行解密,使其恢复成原始数据…...
RIP路由配置
RIP路由配置步骤与命令: 1.启用RIP路由:router rip 2.通告直连网络:network 直连网络 3.启用RIPv2版本:version 2 4.禁用自动汇总:no auto-summary 注意:静态路由通告远程网络,动态路由通告…...
尚硅谷Docker基础篇和Dockerfile超详细整合笔记
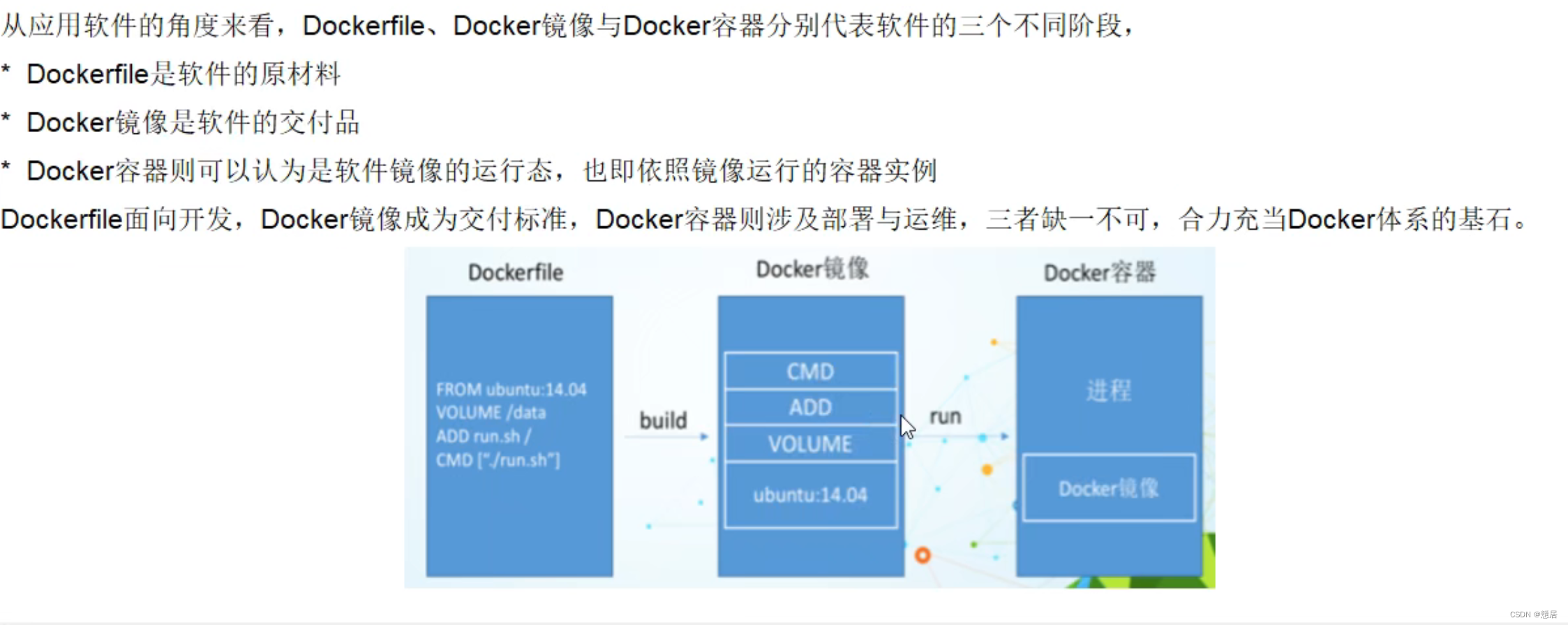
Docker基础篇DockerFile Docker:您要如何确保应用能够在这些环境中运行和通过质量检测?并且在部署过程中不出现令人头疼的版本、配置问题,也无需重新编写代码和进行故障修复?而这个就是使用容器。Docker解决了运行环境和配置问题…...
JavaScript_Date对象_实例方法_get类
计算这一年还剩多少天: <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>Document&…...

Go语言在区块链开发中的应用
引言 区块链是近年来备受关注的技术领域,它不仅改变了传统的数据交换和存储方式,还为各种应用场景提供了全新的解决方案。而Go语言(Golang)作为一门简洁、高效的编程语言,正逐渐成为开发区块链应用的首选语言。本文将…...

S4.2.4.5 Fast Training Sequence (FTS)
一 本章节主讲知识点 1.1 FTS的用途和实现注意 二 本章节原文翻译 Fast Training Sequence (FTS) 主要用于在L0s->L0跳转的过程中,让Receiver 检测到电气空闲退出,以及实现bit 和 symbol lock。 2.1 Gen1 and Gen2 速率 对于Gen1/2 FTS的组成如下…...

Gitlab CICD实用技巧汇总
关于.gitlab-ci.yml的实用配置 1、stage参数 stages: - build - test - deploy 相同stage的作业会并行执行,有一个失败,则认为这个stage失败。 不同stage的作业会按序执行,前面stage有失败,后续stage不会继续执行。 可以使用ne…...
JavaSpringbootMySQL高校实训管理平台01557-计算机毕业设计项目选题推荐(附源码)
目 录 摘要 1 绪论 1.1 研究背景 1.2 研究意义 1.3论文结构与章节安排 2 高校实训管理平台系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1 数据增加流程 2.2.2 数据修改流程 2.2.3 数据删除流程 2.3 系统功能分析 2.3.1 功能性分析 2.3.2 非功能性分析 2.4 系…...

初阶JavaEE(14)表白墙程序
接上次博客:初阶JavaEE(13)(安装、配置:Smart Tomcat;访问出错怎么办?Servlet初识、调试、运行;HttpServlet:HttpServlet;HttpServletResponse)-C…...
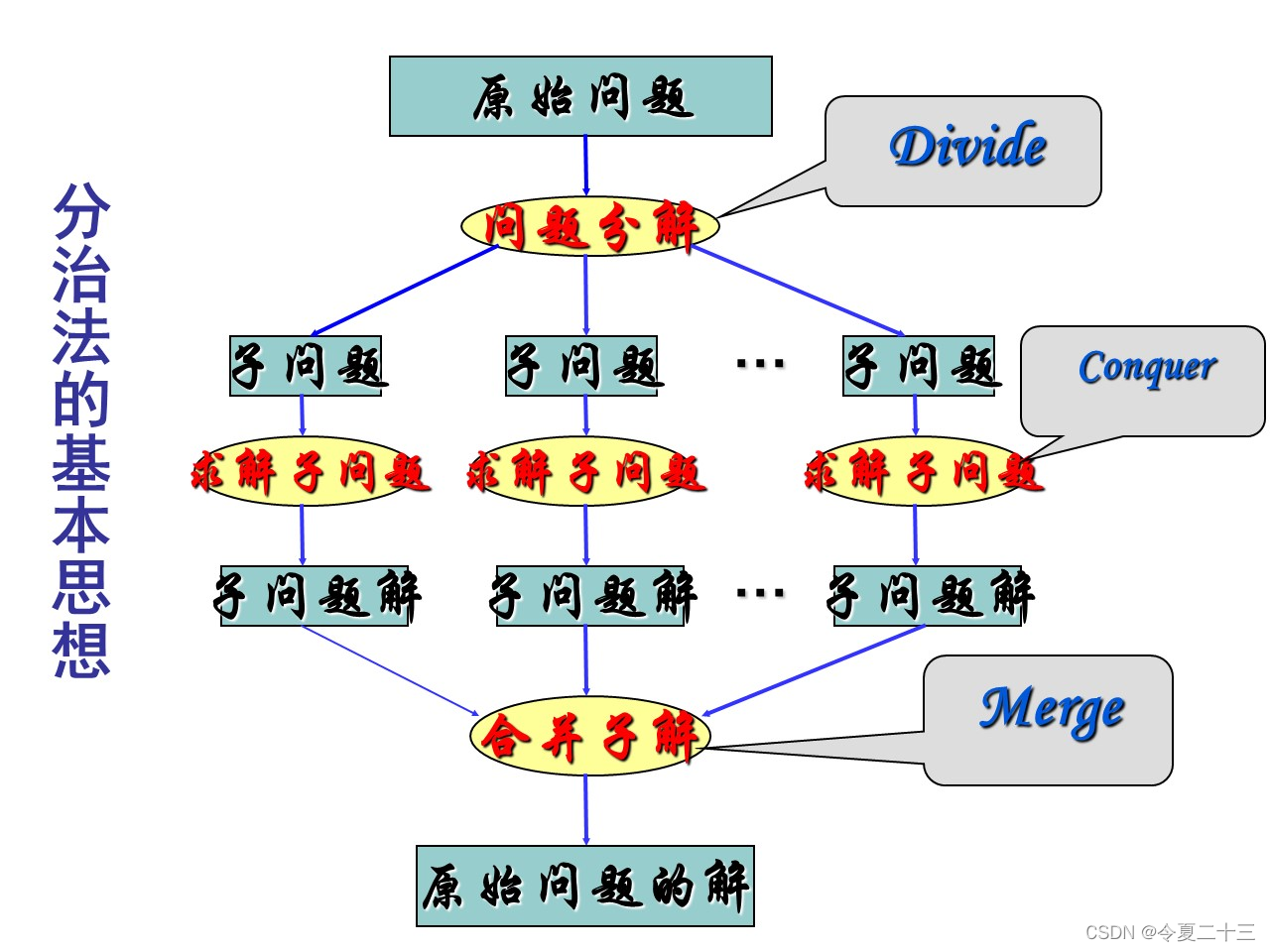
算法设计与分析第二章作业
1. 描述最大字段和的分治算法 题目 思路 判断最大子段和,可以用分治的思想,每次将序列一分为二,选择两个序列的最大子段和。 但是这里还有一种可能,就是子段可以横跨两个子序列,所以我们的最大子段和就是࿱…...

《视觉SLAM十四讲》-- 三维空间的刚体运动
文章目录 02 三维空间的刚体运动2.0 机器人位姿表述2.1 点和坐标系2.1.1 三维坐标系有关表述2.1.2 坐标系变换 2.2 旋转向量和欧拉角2.2.1 旋转向量2.2.2 欧拉角 2.3 四元数2.3.1 四元数的定义2.3.2 四元数的计算2.3.3 四元数表示旋转2.3.4 四元数与其他旋转表示法的转换 2.4 相…...

关于iOS:如何使用SwiftUI调整图片大小?
How to resize Image with SwiftUI? 我在Assets.xcassets中拥有很大的形象。 如何使用SwiftUI调整图像大小以缩小图像? 我试图设置框架,但不起作用: 1 2 Image(room.thumbnailImage) .frame(width: 32.0, height: 32.0) 在Image上应用…...

【MySQL】数据库MySQL基础知识与操作
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《MySQL》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&a…...
)
vim手册(vim cheatsheet)
vim手册(vim cheatsheet) 1. 命令模式 1). 移动光标 在命令模式下,可以使用以下命令来移动光标: - h:向左移动一个字符。 - j:向下移动一行。 - k:向上移动一行。 - l:向右移动一个…...
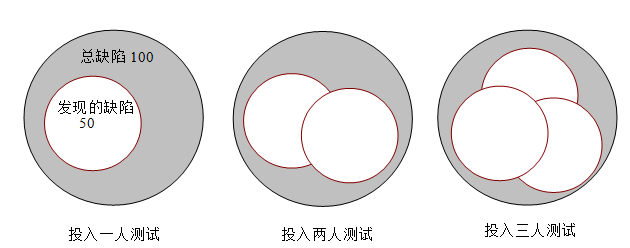
软件测试具体人员分工
最近看了点敏捷测试的东西,看得比较模糊。一方面是因为没有见真实的环境与流程,也许它跟本就没有固定的模式与流程,它就像告诉人们要“勇敢”“努力”。有的人在勇敢的面对生活,有些人在勇敢的挑战自我,有些人在勇敢的…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
