【51nod 连续区间】 题解(序列分治)
题目描述
区间内的元素元素排序后 任意相邻两个元素值差为 1 1 1 的区间称为“连续区间”。
如 3 , 1 , 2 3,1,2 3,1,2 是连续区间, 3 , 1 , 4 3,1,4 3,1,4 不是连续区间。
给出一个 1 ∼ n 1 \sim n 1∼n 的排列,问有多少连续区间。
n ≤ 1 0 6 n \leq 10^6 n≤106
分析
我们考虑对序列分治,设 s o l v e ( l , r ) solve(l,r) solve(l,r) 表示左右端点在区间 [ l , r ] [l, r] [l,r] 内的 “连续区间” 的数量。那么显然, 有:
s o l v e ( l , r ) = s o l v e ( l , m i d ) + s o l v e ( m i d + 1 , r ) + c a l c ( l , r , m i d ) solve(l, r) = solve(l, mid) + solve(mid + 1, r) + calc(l,r, mid) solve(l,r)=solve(l,mid)+solve(mid+1,r)+calc(l,r,mid)
其中 c a l c ( l , r , m i d ) calc(l, r, mid) calc(l,r,mid) 表示左端点在 [ l , m i d ] [l, mid] [l,mid], 右端点在 [ m i d + 1 , r ] [mid + 1, r] [mid+1,r] 的 “连续区间” 数量。
我们接下来考虑如何在 O ( l e n ) O(len) O(len) 的时间复杂度计算 c a l c ( l , r , m i d ) calc(l, r, mid) calc(l,r,mid)。
因为给的序列是 排列,所以有一个性质:对于一个连续区间而言,设它的长度是 k k k,那么有 m a x − m i n + 1 = k max - min + 1= k max−min+1=k,即最大值减最小值等于区间长度。
我们考虑区间 [ i , j ] [i, j] [i,j] 是否为合法区间,其中 i ∈ [ l , m i d ] , j ∈ [ m i d + 1 , r ] i \in [l, mid],j \in [mid + 1, r] i∈[l,mid],j∈[mid+1,r]。
设
m a x x i = m a x ( a i , a i + 1 , a i + 2 , . . . , a m i d ) maxx_i = max(a_i, a_{i + 1}, a_{i + 2},..., a_{mid}) maxxi=max(ai,ai+1,ai+2,...,amid),
m i n x i = m i n ( a i , a i + 1 , a i + 2 , . . . , a m i d ) minx_i = min(a_i, a_{i + 1}, a_{i + 2},..., a_{mid}) minxi=min(ai,ai+1,ai+2,...,amid),
m a x x j = m a x ( a j , a j − 1 , a j − 2 , . . . , a m i d + 1 ) maxx_j = max(a_j, a_{j - 1}, a_{j - 2}, ..., a_{mid + 1}) maxxj=max(aj,aj−1,aj−2,...,amid+1),
m i n x j = m i n ( a j , a j − 1 , a j − 2 , . . . , a m i d + 1 ) minx_j = min(a_j, a_{j - 1}, a_{j - 2}, ..., a_{mid + 1}) minxj=min(aj,aj−1,aj−2,...,amid+1)。
如果区间 [ l , r ] [l, r] [l,r]合法,那么有 m a x ( m a x x i , m a x x j ) − m i n ( m i n x i , m i n x j ) + 1 = j − i + 1 max(maxx_i, maxx_j) - min(minx_i, minx_j) + 1= j - i + 1 max(maxxi,maxxj)−min(minxi,minxj)+1=j−i+1。
把左右加 1 1 1 消掉,得到 m a x ( m a x x i , m a x x j ) − m i n ( m i n x i , m i n x j ) = j − i max(maxx_i, maxx_j) - min(minx_i, minx_j) = j - i max(maxxi,maxxj)−min(minxi,minxj)=j−i。
我们现在只考虑 m a x ( m a x i , m a x j ) max(max_i, max_j) max(maxi,maxj) 等于 m a x i max_i maxi 的情况。另一种情况可以把序列反转后做同样的统计。
那么现在还可以再分两种情况:
1 1 1. m i n ( m i n x i , m i n x j ) = m i n x i min(minx_i, minx_j) = minx_i min(minxi,minxj)=minxi:这一种情况我们可以枚举 i i i,然后根据 m a x x i maxx_i maxxi 和 m i n x x i minxx_i minxxi 的大小算出来一个 j j j,然后检验一下是否满足 m i d + 1 ≤ j ≤ r mid + 1\leq j \leq r mid+1≤j≤r 以及 是否满足 m a x x j < m a x x i maxx_j < maxx_i maxxj<maxxi 并且 m i n x j > m i n x i minx_j > minx_i minxj>minxi 即可。计算和检验的复杂度都是 O ( 1 ) O(1) O(1) 的。
2 2 2. m i n ( m i n x i , m i n x j ) = m i n x j min(minx_i, minx_j) = minx_j min(minxi,minxj)=minxj:那么不难发现, 如果 [ i , j ] [i, j] [i,j] 合法,需要满足 :
m a x x i − m i n x j = j − i ⇒ m a x x i + i = m i n x j + j maxx_i - minx_j = j - i \Rightarrow maxx_i + i = minx_j + j maxxi−minxj=j−i⇒maxxi+i=minxj+j。
因为 m i n x j + j minx_j + j minxj+j 是一个定值, 可以开 桶 记录数量。我们从 m i d mid mid 到 l l l 枚举 i i i, 那么 m a x x i maxx_i maxxi 是不降的, m i n x i minx_i minxi 是不增的。那么由于需要满足 m a x x i > m a x x j maxx_i > maxx_j maxxi>maxxj 并且 m i n x i > m i n x j minx_i > minx_j minxi>minxj,所以我们考虑这两个限制条件相当于是给 j j j 的选择划定了一个范围。
具体来讲,我们维护一个双指针 l t lt lt, r t rt rt。表示在 枚举到 i i i 时 j j j 的范围。 m a x x i maxx_i maxxi 增大那么 r t rt rt 向右移动,在桶里面让 m i n x r t + r t minx_{rt} + rt minxrt+rt 的位置加 1 1 1。 m i n x i minx_i minxi 减小那么让 l t lt lt 向右移动,同时在桶里面让 m i n x l t + l t minx_{lt} + lt minxlt+lt 的位置减 1 1 1。指针稳定后统计 桶里面 m a x x i + i maxx_i + i maxxi+i 位置的数量就好了。
复杂度计算十分典型:
最多递归 l o g 2 n log_2n log2n 层,每一层的总复杂度是 O ( n ) O(n) O(n)。所以算法复杂度是 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)。可能带点常数。
代码不难写。
CODE:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
inline int read(){int x = 0, f = 1; char c = getchar();while(!isdigit(c)){if(c == '-') f = -1; c = getchar();}while(isdigit(c)){x = (x << 1) + (x << 3) + (c ^ 48); c = getchar();}return x * f;
}
int n, a[N], b[N], minx[N], maxx[N], barrel[N * 2];
LL res;
LL get(int l, int r, int k){//k是中间点,属于左边 算左边为主导的答案 maxx[k] = minx[k] = b[k]; maxx[k + 1] = minx[k + 1] = b[k + 1];for(int i = k - 1; i >= l; i--){maxx[i] = max(maxx[i + 1], b[i]);minx[i] = min(minx[i + 1], b[i]);}for(int i = k + 2; i <= r; i++){maxx[i] = max(maxx[i - 1], b[i]);minx[i] = min(minx[i - 1], b[i]);}LL ans = 0;for(int i = k; i >= l; i--){// 首先算左边既有最大,又有最小的答案 int rt = maxx[i] - minx[i] + i;if(rt > r || rt <= k) continue;if(maxx[rt] < maxx[i] && minx[rt] > minx[i]) ans++;}int rt = k + 1, lt = k + 1;for(int i = k; i >= l; i--){// 接下来算左边有最大值,右边有最小值的答案 while(maxx[i] > maxx[rt] && rt <= r){barrel[minx[rt] + rt]++;rt++;}while(minx[i] < minx[lt] && lt < rt){barrel[minx[lt] + lt]--;lt++;}ans += barrel[maxx[i] + i];}for(int i = k + 1; i <= r; i++) barrel[minx[i] + i] = 0;return ans;
}
void solve(int l, int r){if(l == r){res++; return ;}int mid = (l + r >> 1);solve(l, mid); solve(mid + 1, r);// 算出来左右两边的答案 for(int i = l; i <= r; i++) b[i] = a[i];res += get(l, r, mid);reverse(b + l, b + r + 1);res += get(l, r, l + r - mid - 1);
}
int main(){n = read();for(int i = 1; i <= n; i++)a[i] = read();solve(1, n);printf("%lld\n", res);return 0;
}
相关文章:
)
【51nod 连续区间】 题解(序列分治)
题目描述 区间内的元素元素排序后 任意相邻两个元素值差为 1 1 1 的区间称为“连续区间”。 如 3 , 1 , 2 3,1,2 3,1,2 是连续区间, 3 , 1 , 4 3,1,4 3,1,4 不是连续区间。 给出一个 1 ∼ n 1 \sim n 1∼n 的排列,问有多少连续区间。 …...

10.30校招 实习 内推 面经
绿*泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表格 1、校招|极目智能2024届校招 校招|极目智能2024届校招 2、校招|杭州极弱磁场国家重大科技基础设施研究院2024秋季校园招聘正式启动! 校招&…...

相比typescript,python的动态类型有什么优缺点?
以下是Python的动态类型相对于TypeScript的静态类型的一些优缺点: 1、Python的动态类型优点: 更灵活:Python的动态类型允许你在运行时更灵活地改变变量的类型,这对于快速原型设计和快速开发非常有帮助。 代码更简洁:…...
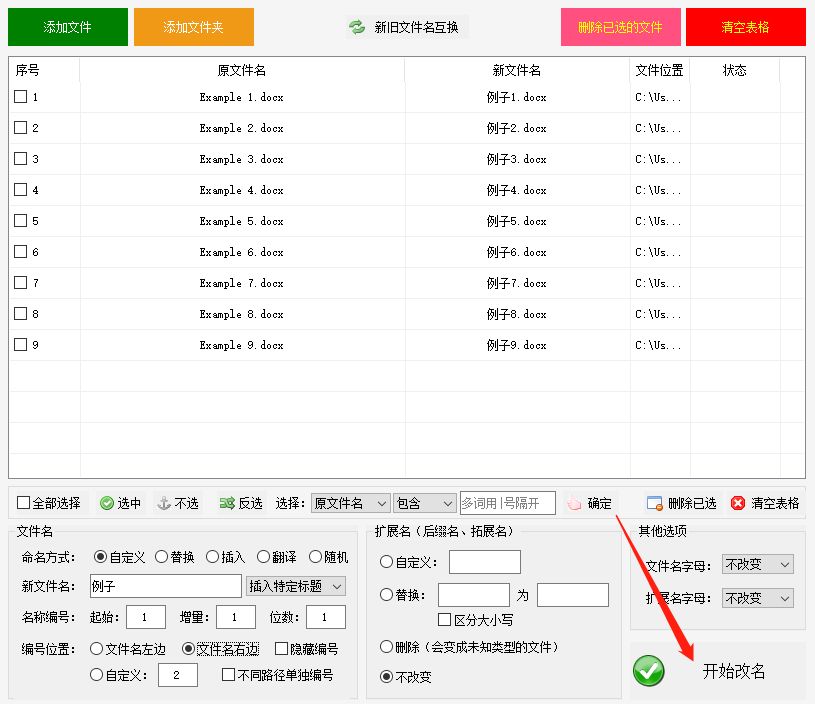
高效处理文件:批量顺序编号重命名方法
每个人都面临着文件管理的挑战,特别是那些需要处理大量文件的人。如何高效地管理这些文件一直是一个难题。为了解决这个问题,我向大家推荐一款强大的文件管理工具——固乔文件管家。这个工具可以帮助你快速有效地给文件进行批量重命名和编号,…...

JAVA深化篇_29—— 线程使用之线程联合以及Thread类中的其他常用方法【附有详细说明及代码案例】
线程联合 当前线程邀请调用方法的线程优先执行,在调用方法的线程执行结束之前,当前线程不能再次执行。线程A在运行期间,可以调用线程B的join()方法,让线程B和线程A联合。这样,线程A就必须等待线程B执行完毕后…...
)
〖Python网络爬虫实战㊲〗- JavaScript 逆向实战(一)
订阅:新手可以订阅我的其他专栏。免费阶段订阅量1000+python项目实战 Python编程基础教程系列(零基础小白搬砖逆袭) 说明:本专栏持续更新中,订阅本专栏前必读关于专栏〖Python网络爬虫实战〗转为付费专栏的订阅说明作者:爱吃饼干的小白鼠。Python领域优质创作者,2022年度…...

2023辽宁省数学建模A题铁路车站的安全标线完整原创论文详细讲解(含matlab代码)
大家好呀,从发布赛题一直到现在,总算完成了辽宁省数学建模A题完整的成品论文。 本论文可以保证原创,保证高质量。绝不是随便引用一大堆模型和代码复制粘贴进来完全没有应用糊弄人的垃圾半成品论文。 B预计下午两点前更新完毕,A全…...
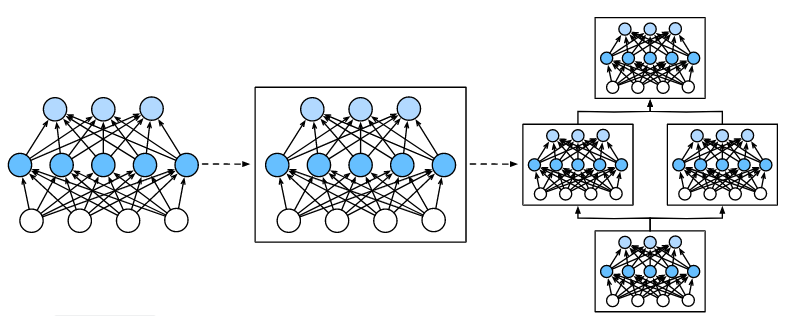
(14)学习笔记:动手深度学习(Pytorch神经网络基础)
文章目录 神经网络的层与块块的基本概念自定义块 问答 神经网络的层与块 块的基本概念 以多层感知机为例, 整个模型接受原始输入(特征),生成输出(预测), 并包含一些参数(所有组成层…...

Leetcode-1 两数之和
暴力穷举 class Solution {public int[] twoSum(int[] nums, int target) {int[] num new int[2];for(int i0;i<nums.length-1;i){for(int ji1;j<nums.length;j){if(nums[i]nums[j]target){num[0]i;num[1]j;}}}return num;} }HashMap,记录下标和对应值&…...
Screens for Mac 中文版 远程桌面连接控制工具
Screens Mac 版是Mac os平台上的一款Mac VNC 客户终端,能够自由访问远程计算机设备, Screens Mac 版支持各种强大的远程控制辅助工具,例如剪切板共享、快捷方式自定义、安全连接、多屏幕支持、快速扫描连接等。 Screens 4 for mac支持多种远程桌面协议&…...
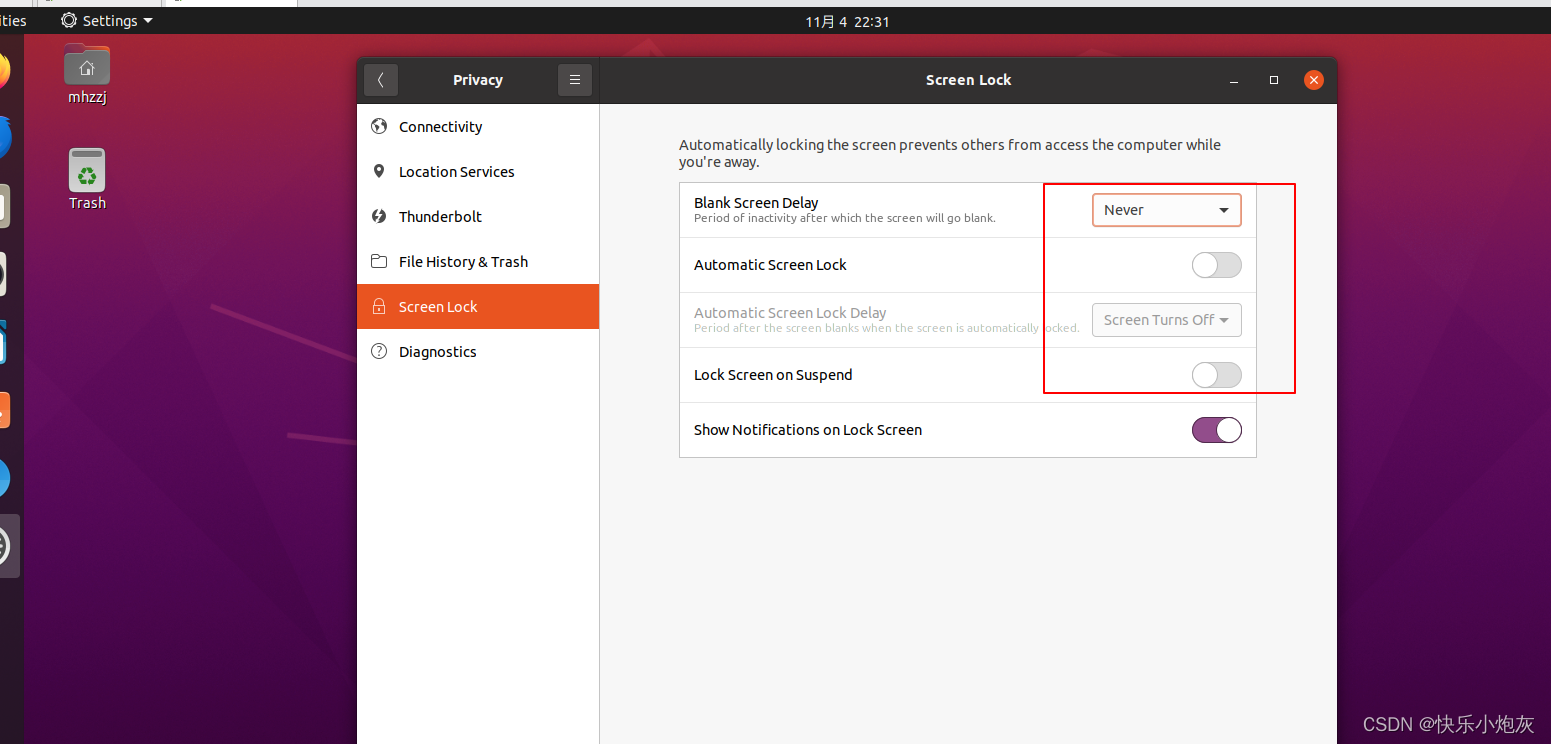
解决vmware安装ubuntu虚拟机显示不全以及无法实现windows与虚拟机之间无法相互复制粘贴问题
01、存在问题 02、解决方案 sudo apt-get autoremove open-vm-tools sudo apt-get install open-vm-tools sudo apt-get install open-vm-tools-desktop reboot //重启重启后界面如下: 存在Bug 如果遇到一下问题,请先执行下列命令&#x…...

希腊字母读音表
序号大写小写英文注音国际音标注音中文读音意义1Ααalphaa:lf阿尔法角度;系数2Ββbetabet贝塔磁通系数;角度;系数3Γγgammaˈɡmə伽马电导系数(小写)4Δδdeltadelt德尔塔变动;密度;屈光度5…...
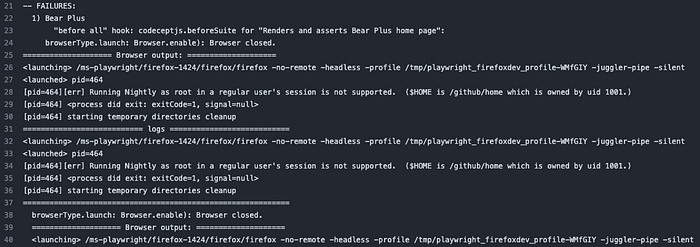
如何使用CodeceptJS、Playwright和GitHub Actions构建端到端测试流水线
介绍 端到端测试是软件开发的一个重要方面,因为它确保系统的所有组件都能正确运行。CodeceptJS是一个高效且强大的端到端自动化框架,与Playwright 结合使用时,它成为自动化Web、移动甚至桌面 (Electron.js) 应用程序比较好用的工具。 在本文中…...

解析python爬取Ebay数据的方式
前言 Ebay是全球著名的电子商务平台之一,每天都有海量的商品信息涌入其中,在电商行业获取这些数据试试非常有价值的,为了更好地了解市场动态,掌握更多的电商行情。Python爬虫成为了必不可少的工具,本文将通过使用Http…...
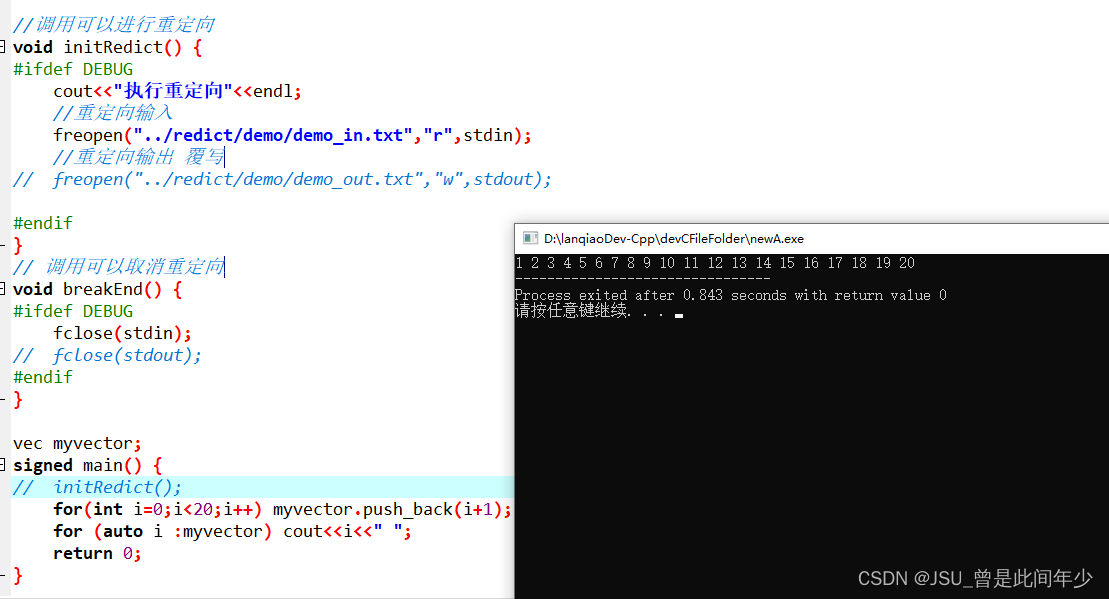
设置DevC++支持c++11标准
1.点击编译选项 2. 设置语言标准 3.点击确认 4.测试代码 使用auto成功 测试!...

腾讯云服务器CVM详细介绍_优缺点亲自整理
腾讯云服务器CVM提供安全可靠的弹性计算服务,腾讯云明星级云服务器,弹性计算实时扩展或缩减计算资源,支持包年包月、按量计费和竞价实例计费模式,CVM提供多种CPU、内存、硬盘和带宽可以灵活调整的实例规格,提供9个9的数…...
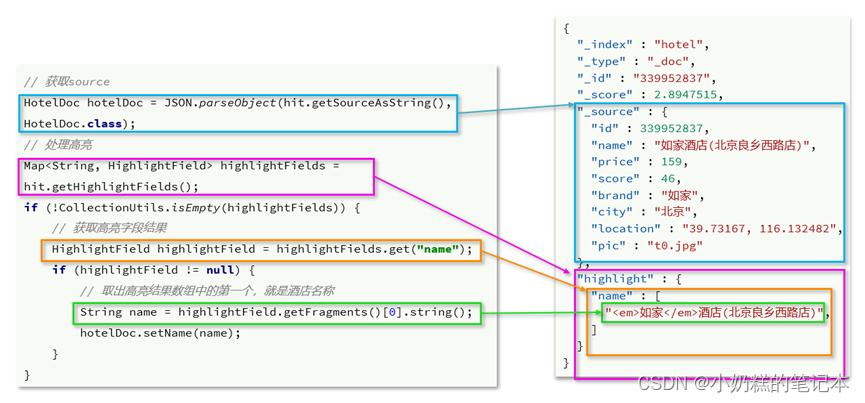
06_es分布式搜索引擎2
一、DSL查询文档 1.DSL查询分类 ①查询所有:match_all ②全文检索:利用分词器对用户输入的内容分词,倒排索引去匹配 match_query multi_match_query ③精确查询:根据精确词条查找数据,查找的是keyword,数值,日期,b…...

【3D图像分割】基于 Pytorch 的 VNet 3D 图像分割3(3D UNet 模型篇)
在本文中,主要是对3D UNet 进行一个学习和梳理。对于3D UNet 网上的资料和GitHub直接获取的代码很多,不需要自己从0开始。那么本文的目的是啥呢? 本文就是想拆解下其中的结构,看看对于一个3D的UNet,和2D的UNet&#x…...
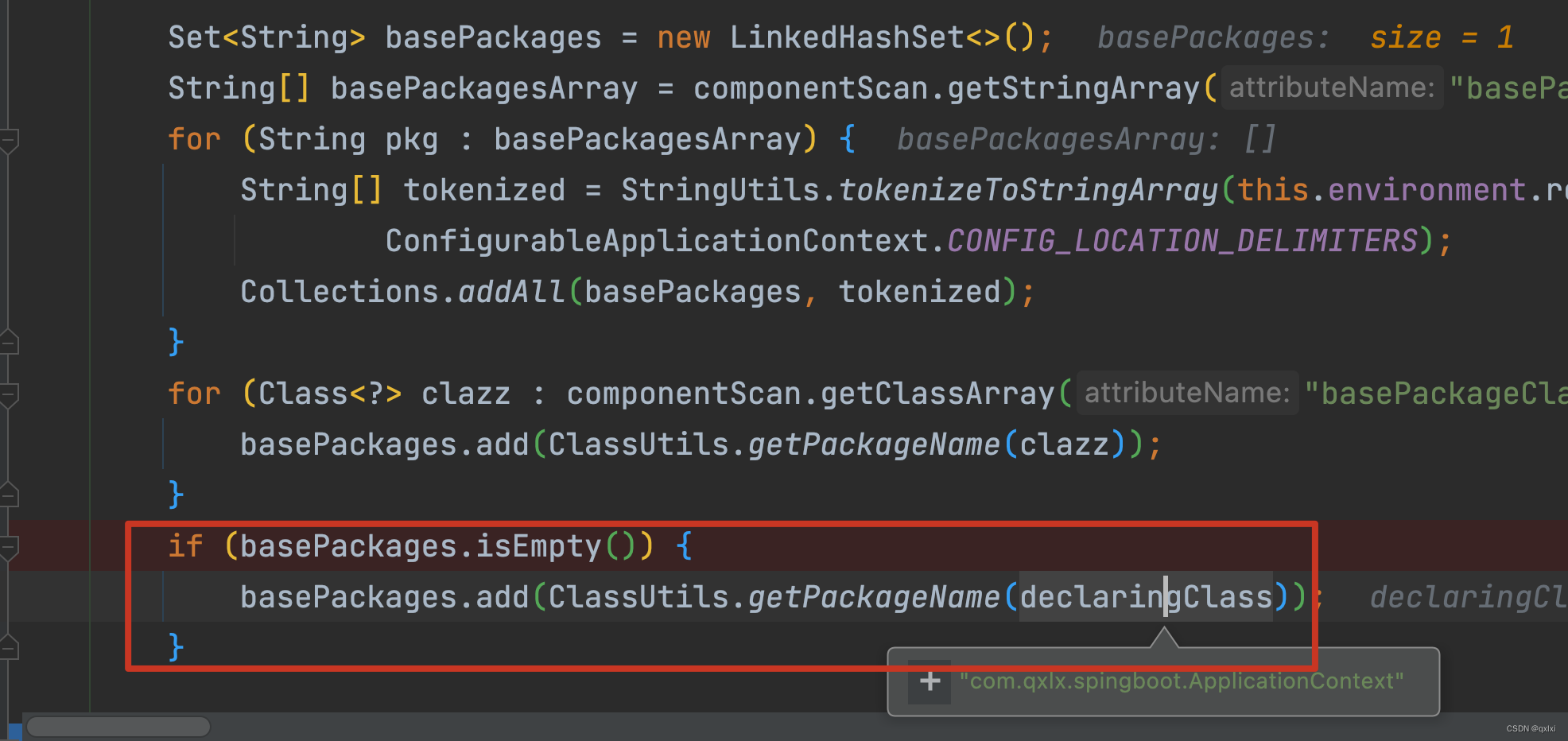
【源码解析】Spring Bean定义常见错误
案例1 隐式扫描不到Bean的定义 RestController public class HelloWorldController {RequestMapping(path "/hiii",method RequestMethod.GET)public String hi() {return "hi hellowrd";}}SpringBootApplication RestController public class Applicati…...

由于找不到vcruntime140.dll无法继续执行代码
在计算机使用过程中,我们可能会遇到一些错误提示,其中之一就是“vcruntime140.dll丢失”。这个错误通常发生在运行某些程序或游戏时,它会导致程序无法正常运行。那么,如何解决vcruntime140.dll丢失的问题呢?本文将介绍…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...
