求极限Lim x-＞0 (x-sinx)*e-²x / (1-x)⅓
题目如下：
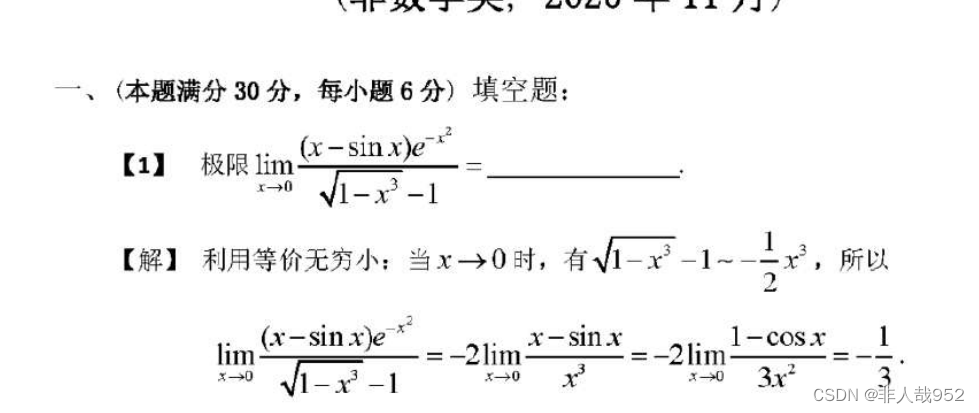
解题思路:
这题运用了无穷小替换、洛必达法则、求导法则
具体解题思路如下:
1、首先带入x趋近于0，可以得到（0*1）/0，所以可以把e的-x的平方沈略掉
然后根据无穷小替换，利用t趋近于0时，(1+t)的n分之一次方 趋近于t/n
此题中替换 (1+(-x的3次方))的二分之一次方，变成-x的平方/2
3、然后洛必达法则，“0/0型” 分子分母同事求导，极限值不变
相关文章：
求极限Lim x-＞0 (x-sinx)*e-²x / (1-x)⅓
题目如下： 解题思路: 这题运用了无穷小替换、洛必达法则、求导法则 具体解题思路如下: 1、首先带入x趋近于0，可以得到（0*1）/0，所以可以把e的-x的平方沈略掉 然后根据无穷小替换，利用t趋近于0时…...
JavaScript数据类型详细解析与代码实例
JavaScript是一种弱类型动态语言，数据类型分为原始类型和对象类型。 原始类型 原始类型包括：数字、字符串、布尔值和undefined、null。 数字 JavaScript中的数字类型包括整数和浮点数，可以进行基本的数学运算。 var num1 10; // 整数 v…...
.NET Framework中自带的泛型委托Func
Func<>是.NET Framework中自带的泛型委托，可以接收一个或多个输入参数，并且有返回值，和Action类似，.NET基类库也提供了多达16个输入参数的Func委托，输出参数只有1个。 1、Func泛型委托 .NET Framework为我们提…...
深入理解JVM虚拟机第十七篇：虚拟机栈中栈帧的内部结构
大神链接：作者有幸结识技术大神孙哥为好友，获益匪浅。现在把孙哥视频分享给大家。 孙哥链接：孙哥个人主页 作者简介：一个颜值99分，只比孙哥差一点的程序员 本专栏简介：话不多说，让我们一起干翻JavaScript 本文章简介：话不多说，让我们讲清楚虚拟机栈存储结构和运行原理…...
uniapp中地图定位功能实现的几种方案
1.uniapp自带uni.getLocation uni.getLocation(options) getlocation | uni-app官网 实现思路：uni.getLocation获取经纬度后调用接口获取城市名 优点：方便快捷，直接调用 缺点：关闭定位后延时很久，无法控制定位延迟…...
JS功能实现
目录 轮播图移动端轮播图按下回车发表评论tab栏切换全选按钮 轮播图 <style>* {box-sizing: border-box;}.slider {width: 560px;height: 400px;overflow: hidden;}.slider-wrapper {width: 100%;height: 320px;}.slider-wrapper img {width: 100%;height: 100%;display:…...
connect-history-api-fallback原理
connect-history-api-fallback是一个用于处理前端路由的中间件，它的原理是在服务器接收到请求时，检查请求的路径是否匹配到静态文件（如HTML、CSS、JS等），如果不匹配，则将请求重定向到前端的入口文件&#x…...
Android ConstraintLayout分组堆叠圆角ShapeableImageView
Android ConstraintLayout分组堆叠圆角ShapeableImageView <?xml version"1.0" encoding"utf-8"?> <androidx.constraintlayout.widget.ConstraintLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"…...
Docker Stack部署应用详解+Tomcat项目部署详细实战
Docker Stack 部署应用 概述 单机模式下，可以使用 Docker Compose 来编排多个服务。Docker Swarm 只能实现对单个服务的简单部署。而Docker Stack 只需对已有的 docker-compose.yml 配置文件稍加改造就可以完成 Docker 集群环境下的多服务编排。 stack是一组共享…...
Compose-Multiplatform在Android和iOS上的实践
本文字数：4680字 预计阅读时间：30分钟 01 简介 之前我们探讨过KMM，即Kotlin Multiplatform Mobile，是Kotlin发布的移动端跨平台框架。当时的结论是KMM提倡将共有的逻辑部分抽出，由KMM封装成Android(Kotlin/JVM)的aar和…...
XXL-JOB 默认 accessToken 身份绕过导致 RCE
文章目录 0x01 漏洞介绍0x02 影响版本0x03 环境搭建0x04 漏洞复现第一步 访问页面返回报错信息第二步 执行POC,进行反弹shell第三步 获取shell0x05 修复建议摘抄免责声明0x01 漏洞介绍 XXL-JOB 是一款开源的分布式任务调度平台，用于实现大规模任务的调度和执行。 XXL-JOB 默…...
7 库函数之复位和时钟设置（RCC）所有函数的介绍及使用
7 库函数之复位和时钟设置（RCC）所有函数的介绍及使用的介绍及使用 1. 图片有格式二、RCC库函数固件库函数预览2.1 函数RCC_DeInit2.2 函数RCC_HSEConfig2.3 函数RCC_WaitForHSEStartUp2.4 函数RCC_AdjustHSICalibrationValue2.5 函数RCC_HSICmd2.6 函数RCC_PLLConfig2.7 函数…...
第十七节——指令
一、概念 在Vue.js中，指令（Directives）是一种特殊的语法，用于为HTML元素添加特定的行为和功能。指令以v-作为前缀，通过在HTML标签中使用这些指令来操作DOM，修改元素的属性、样式或行为。 Vue.js提供了一组…...
优雅的 Dockerfile 是怎样炼成的？
Docker 简介 目前，Docker 主要有两个形态：Docker Desktop 和 Docker Engine。 Docker Desktop 是专门针对个人使用而设计的，支持 Mac（已支持arm架构的M系芯片） 和 Windows 快速安装，具有直观的图形界面&a…...
2023-2024 中国科学引文数据库来源期刊列表（CSCD）
文章目录 CSCD来源期刊遴选报告2023-2024 中国科学引文数据库来源期刊列表（CSCD） CSCD来源期刊遴选报告 2023-2024 中国科学引文数据库来源期刊列表（CSCD）...
【3D图像分割】基于Pytorch的VNet 3D图像分割5（改写数据流篇）
在这篇文章：【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割2（基础数据流篇） 的最后，我们提到了： 在采用vent模型进行3d数据的分割训练任务中，输入大小是16*96*96，这个的裁剪是放到Dataset类…...
WebSocket Day02 : 握手连接
前言 握手连接是WebSocket建立通信的第一步，通过客户端和服务器之间的一系列握手操作，确保了双方都支持WebSocket协议，并达成一致的通信参数。握手连接的过程包括客户端发起握手请求、服务器响应握手请求以及双方完成握手连接。完成握手连接后…...
c#的反编译工具ISPY和net reflector 使用比较
我有一份Asp.net程序需要修改，但没有源码，只有dll，需要使用反编译工具回复源码，尝试使用了市面上的两种主流的工具ISPY和net reflector ，最终用ISPY恢复了源码。 比较 ISPY 恢复的代码和实际有差距，但还能…...
基于LDA主题+协同过滤+矩阵分解算法的智能电影推荐系统——机器学习算法应用(含python、JavaScript工程源码)+MovieLens数据集（四）
目录 前言总体设计系统整体结构图系统流程图 运行环境模块实现1. 数据爬取及处理2. 模型训练及保存3. 接口实现4. 收集数据5. 界面设计 系统测试相关其它博客工程源代码下载其它资料下载 前言 前段时间，博主分享过关于一篇使用协同过滤算法进行智能电影推荐系统的博…...
方阵行列式与转置矩阵
1.转置矩阵：格式规定：如果矩阵A为n阶方阵，那么A的T次方为矩阵A的转置矩阵，即将矩阵A的行与列互换。 2.转置矩阵的运算性质： 1.任何方阵的转置矩阵的转置矩阵为方阵自身。 2.多个矩阵的和的转置矩阵等于多个转置矩阵的…...
Java 8 Stream API 入门到实践详解
一、告别 for 循环！ 传统痛点： Java 8 之前，集合操作离不开冗长的 for 循环和匿名类。例如，过滤列表中的偶数： List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...
Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
屋顶变身“发电站” ，中天合创屋面分布式光伏发电项目顺利并网！
5月28日，中天合创屋面分布式光伏发电项目顺利并网发电，该项目位于内蒙古自治区鄂尔多斯市乌审旗，项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站，总装机容量为9.96MWp。 项目投运后，每年可节约标煤3670…...
【Oracle】分区表
个人主页：Guiat 归属专栏：Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
如何在网页里填写 PDF 表格？
有时候，你可能希望用户能在你的网站上填写 PDF 表单。然而，这件事并不简单，因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件，但原生并不支持编辑或填写它们。更糟的是，如果你想收集表单数据ÿ…...
Java求职者面试指南：Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南：Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问（基础概念问题） 1. 请解释Spring框架的核心容器是什么？它在Spring中起到什么作用？ Spring框架的核心容器是IoC容器&#…...
LRU 缓存机制详解与实现（Java版） + 力扣解决
📌 LRU 缓存机制详解与实现（Java版） 一、📖 问题背景 在日常开发中，我们经常会使用 缓存（Cache） 来提升性能。但由于内存有限，缓存不可能无限增长，于是需要策略决定&am…...
R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中，科研绘图是必不可少的，一张好看的图形会是文章很大的加分项。 为了便于使用，本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中，获取方式： R 语言科研绘图模板 --- sciRplothttps://mp.…...
第7篇：中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中，可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中，必须做到： 🔍 追踪每一条 SQL 的生命周期（从入口到数据库执行）&#…...
Vite中定义@软链接
在webpack中可以直接通过符号表示src路径，但是vite中默认不可以。 如何实现： vite中提供了resolve.alias：通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...