容斥恒等式的证明
容斥恒等式的证明
推广公式
P(A∪B)=P(A)+P(B)−P(A∩B)P(A\cup B)=P(A)+P(B)-P(A\cap B) P(A∪B)=P(A)+P(B)−P(A∩B)
(a)设A、B、C为三个事件,则下列恒等式成立:
P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C) P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)
(b)设A1A_1A1,A2A_2A2,A3A_3A3,…,AnA_nAn为n个事件,令S1S_1S1={i∣1≤i≤ni|1\leq i \leq ni∣1≤i≤n},S2S_2S2={(i1,i2)∣1≤i1<i2≤n(i_1,i_2)|1\leq i_1 < i_2 \leq n(i1,i2)∣1≤i1<i2≤n},一般的,令S1S_1S1为满足条件$ \le i_1 < i_2<… < i_m\le n的m维指标,(的m维指标,(的m维指标,(i_1,…i_m$)的集合,则下列恒等式成立:
P(∪k=1nAk)=∑i∈S1P(Ai)−∑(i1,i2)∈S2P(Ai1∩Ai2)+∑i1,i2,i3∈S3P(Ai1∩Ai2∩Ai3)−...+(−1)n−1P(∩k=1nAk)P(\cup^n_{k=1}A_k)=\displaystyle \sum_{i\in S_1}P(A_i)-\displaystyle\sum_{(i_1,i_2)\in S_2}P(A_{i_1} \cap A_{i_2})+\displaystyle \sum_{i_1,i_2,i_3 \in S_3}P(A_{i_1} \cap A_{i_2} \cap A_{i_3})-...+(-1)^{n-1}P(\cap^n_{k=1}A_{k})P(∪k=1nAk)=i∈S1∑P(Ai)−(i1,i2)∈S2∑P(Ai1∩Ai2)+i1,i2,i3∈S3∑P(Ai1∩Ai2∩Ai3)−...+(−1)n−1P(∩k=1nAk)
解:(a)利用公式P(X∪Y)=P(X)+P(Y)−P(X∩Y)P(X\cup Y)=P(X)+P(Y)-P(X\cap Y)P(X∪Y)=P(X)+P(Y)−P(X∩Y)和(A∪B)∩C=(A∩C)∪(B∩C)(A\cup B)\cap C=(A\cap C)\cup (B\cap C)(A∪B)∩C=(A∩C)∪(B∩C),我们有
P(A∪B∪C)=P(A∪B)+P(C)−P((A∪B)∩C)=P(A∪B)+P(C)−P((A∩C)∪(B∩C))=P(A∪B)+P(C)−P(A∩C)−P(B∩C)+P(A∩B∩C)=P(A)+P(B)−P(A∩B)+P(C)−P(A∩C)−P(B∩C)+P(A∩B∩C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)P(A\cup B\cup C)=P(A\cup B)+P(C)-P((A\cup B )\cap C) \\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =P(A\cup B)+P(C)-P((A\cap C )\cup (B\cap C))\\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =P(A\cup B)+P(C)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C) \\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =P(A)+P(B)-P(A\cap B)+P(C)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C) \\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C)P(A∪B∪C)=P(A∪B)+P(C)−P((A∪B)∩C) =P(A∪B)+P(C)−P((A∩C)∪(B∩C)) =P(A∪B)+P(C)−P(A∩C)−P(B∩C)+P(A∩B∩C) =P(A)+P(B)−P(A∩B)+P(C)−P(A∩C)−P(B∩C)+P(A∩B∩C) =P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)
(b)利用归纳法,主要推断部分可以模仿(a)中步骤
n=2时,P(A∪B)=P(A)+P(B)−P(A∩B)P(A\cup B)=P(A)+P(B)-P(A\cap B)P(A∪B)=P(A)+P(B)−P(A∩B).
假设n=k-1,有
P(∪k=1k−1Ak)=∑i∈S1P(Ai)−∑(i1,i2)∈S2P(Ai1∩Ai2)+∑i1,i2,i3∈S3P(Ai1∩Ai2∩Ai3)−...+(−1)n−2P(∩k=1k−1Aik)P(\cup^{k-1}_{k=1}A_k)=\displaystyle \sum_{i\in S_1}P(A_i)-\displaystyle\sum_{(i_1,i_2)\in S_2}P(A_{i_1} \cap A_{i_2})+\displaystyle \sum_{i_1,i_2,i_3 \in S_3}P(A_{i_1} \cap A_{i_2} \cap A_{i_3})-...+(-1)^{n-2}P(\cap^{k-1}_{k=1}A_{i_k})P(∪k=1k−1Ak)=i∈S1∑P(Ai)−(i1,i2)∈S2∑P(Ai1∩Ai2)+i1,i2,i3∈S3∑P(Ai1∩Ai2∩Ai3)−...+(−1)n−2P(∩k=1k−1Aik)
则n=k时,P(∪k=1nAk)=P(∪k=1k−1Ak∪Ak)P(\cup^n_{k=1}A_k)=P(\cup^{k-1}_{k=1}A_k\cup A_k)P(∪k=1nAk)=P(∪k=1k−1Ak∪Ak)
令∪i=1k−1Ai=B\cup^{k-1}_{i=1}A_i=B∪i=1k−1Ai=B,
P(∪k=1nAk)=P(B∪Ak)P(\cup^n_{k=1}A_k)=P(B\cup A_k)P(∪k=1nAk)=P(B∪Ak)
所以,
P(∪k=1nAk)=P(B∪Ak)=P(B)+P(Ak)−P(B∩Ak)P(\cup^n_{k=1}A_k)=P(B\cup A_k)=P(B)+P(A_k)-P(B\cap A_k)P(∪k=1nAk)=P(B∪Ak)=P(B)+P(Ak)−P(B∩Ak) (1)
前两个地方都很好推导,主要是最后一项。
P(B∩Ak)=P(∪i=1k−1AiAk)=∑i=1k−1P(AiAk)+(−11)∑1≤i1<i2≤ik−1P(Ai1Ai2Ak)+...+(−1)k−2P(A1A2...Ak)P(B\cap A_k)=P(\cup^{k-1}_{i=1}A_iA_k)\\=\displaystyle \sum_{i=1}^{k-1}P(A_iA_k)+(-1^1) \displaystyle \sum_{1\le i_1<i_2\le i_{k-1}}P(A_{i_1}A_{i_2}A_k)+...+(-1)^{k-2}P(A_1A_2...A_k)P(B∩Ak)=P(∪i=1k−1AiAk)=i=1∑k−1P(AiAk)+(−11)1≤i1<i2≤ik−1∑P(Ai1Ai2Ak)+...+(−1)k−2P(A1A2...Ak) (2)
把(2)带入(1),
得到:
P(∪k=1nAk)=∑i∈S1P(Ai)−∑(i1,i2)∈S2P(Ai1∩Ai2)+∑i1,i2,i3∈S3P(Ai1∩Ai2∩Ai3)−...+(−1)n−1P(∩k=1nAk)P(\cup^n_{k=1}A_k)=\displaystyle \sum_{i\in S_1}P(A_i)-\displaystyle\sum_{(i_1,i_2)\in S_2}P(A_{i_1} \cap A_{i_2})+\displaystyle \sum_{i_1,i_2,i_3 \in S_3}P(A_{i_1} \cap A_{i_2} \cap A_{i_3})-...+(-1)^{n-1}P(\cap^n_{k=1}A_{k})P(∪k=1nAk)=i∈S1∑P(Ai)−(i1,i2)∈S2∑P(Ai1∩Ai2)+i1,i2,i3∈S3∑P(Ai1∩Ai2∩Ai3)−...+(−1)n−1P(∩k=1nAk)
得证。
相关文章:

容斥恒等式的证明
容斥恒等式的证明 推广公式 P(A∪B)P(A)P(B)−P(A∩B)P(A\cup B)P(A)P(B)-P(A\cap B) P(A∪B)P(A)P(B)−P(A∩B) (a)设A、B、C为三个事件,则下列恒等式成立: P(A∪B∪C)P(A)P(B)P(C)−P(A∩B)−P(A∩C)−P(B∩C)P(A∩B∩C)P(A\cup B\cup C)P(A)P(B)P(C)…...

Java中的this与super关键字深度解析
一、this关键字this 关键字是 Java 常用的关键字,可用于任何实例方法内指向当前对象,也可指向对其调用当前方法的对象,或者在需要当前类型对象引用时使用。(1)this.属性名this修饰的变量用于指代成员变量方法的形参如果…...

CSS3新增的视口单位Vh、Vw单位
定义vw:浏览器可见视口【宽度】的百分比(1vw代表视窗【宽度】的1%)vh:浏览器可见视口【高度】的百分比(1vw代表视窗【高度】的1%)vmin:当前 vw 和 vh 较小的一个值。vmax:当前 vw 和…...
【Linux】yum安装docker指定版本
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录卸载已有的docker部署指定版本docker安…...
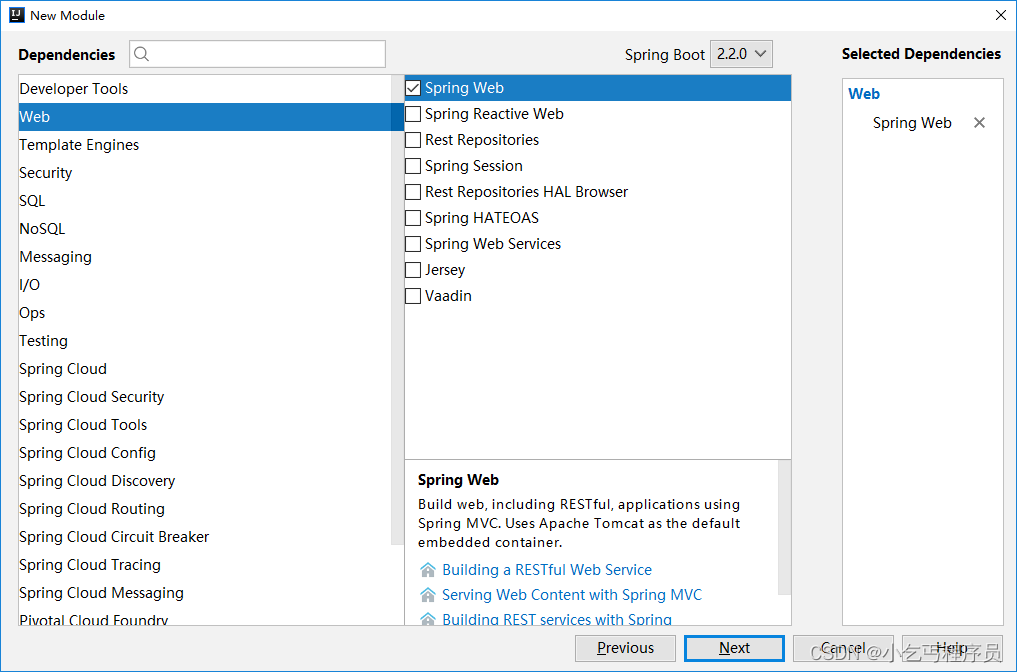
SpringBoot相关操作
01-今日内容 Spring概述、快速入门SpringBoot配置SpringBoot整合 02-SpringBoot概述 SpringBoot提供了一种快速使用Spring的方式,基于约定优于配置的思想,可以让开发人员不必在配置与逻辑业务之间进行思维的切换,全身心的投入到逻辑业务的…...
函数:调用父类的构造方法)
Python super()函数:调用父类的构造方法
Python 中子类会继承父类所有的类属性和类方法。严格来说,类的构造方法其实就是实例方法,因此毫无疑问,父类的构造方法,子类同样会继承。 但我们知道,Python 是一门支持多继承的面向对象编程语言,如果子类…...
@ConfigurationProperties在方法上的使用
文章目录1. 前言2. 先说结论3. 代码解释1. Component ConfigurationProperties2. EnableConfigurationProperties ConfigurationProperties3. Bean ConfigurationProperties1. 前言 在学习spring的时候,ConfigurationProperties应该经常被使用到,作用…...
)
【QT】如何查找和获取界面上的子部件(findChild 和 findChidren)
目录1. findChild()函数2. findChildren()函数3. 示例1. findChild()函数 函数原型: T QObject::findChild(const QString &name QString(), Qt::FindChildOptions options Qt::FindChildrenRecursively) const返回该对象的子对象,该子对象可以转…...

MIT 6.S081学习笔记
计划花25天时间学完6.S081课程,从2月20日-3月20日。课程主页Link xv6 book GDB User Manual Lecture 1: Introduction and Examples课程主题:设计和实现操作系统 OS的三大功能:多路复用、隔离和交互。 Lab: Xv6 and Unix utiliti…...
《网络安全入门到精通》 - 2.1 - Windows基础 - DOS命令Windows防火墙Windows共享文件
「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「订阅专栏」:此文章已录入专栏《网络安全入门到精通》 Windows基础一、DOS命令1、目录文件操作dir 列出目录文件cd 切换目录md 创建目录rd 删除目录move 移动文件或目…...
八、Vben框架动态生成可编辑Table
开发过程中产品经理提出了一些奇怪的需求,让人很摸不着头脑,一问就是客户的需求就是这样,那么我们开发只能想各种办法啦。 最近就提出了两个需求, 第一个是需要在日期选择的时候根据时间选择的不同让底下table中增加两个时间中间的…...

浅谈ERP数据的重要性
影响一个ERP项目的因素有很多,数据无疑是其中很重要的一项,正所谓“正确的诊断源于准确的信息,准确的信息基于可靠的采集”,当我们抓住数据这个根基,大处着眼,小处着手的时候,我们距离ERP成功的日子就不会太…...

【RabbitMQ笔记06】消息队列RabbitMQ七种模式之Topics主题模式
这篇文章,主要介绍消息队列RabbitMQ七种模式之Topics主题模式。 目录 一、消息队列 1.1、主题模式(Topics) 1.2、案例代码 (1)引入依赖 (2)编写生产者 (3)编写消费…...

ChatGPT似乎有的时候并不能搞懂Java的动态分派,你懂了吗?
目录 碎碎念 ChatGPT 中出现的问题 那么正确答案应该是什么呢? 分派的相关知识点总结: 分派是什么? 静态分派与动态分派: Java语言是静态多分派,动态单分派的; 静态分派:静态重载多分派…...
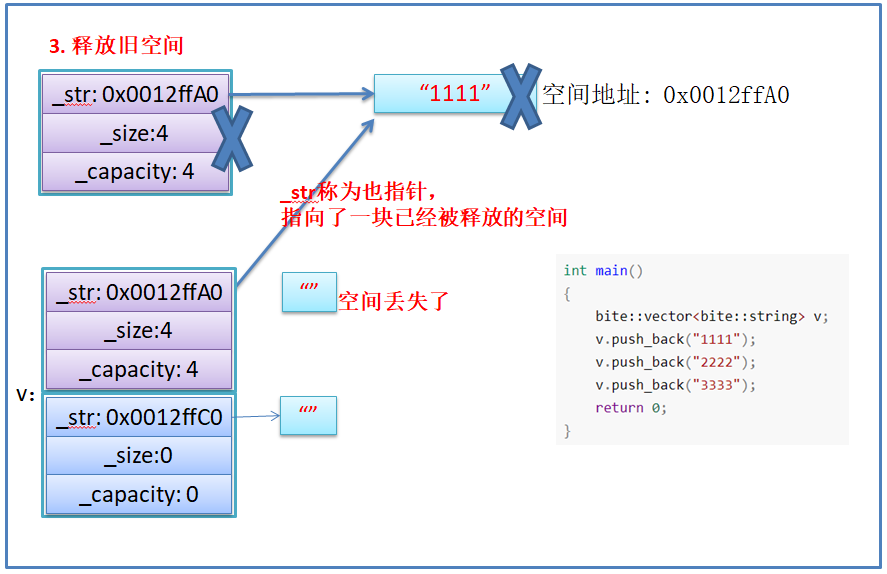
【C++初阶】vector的模拟实现
大家好我是沐曦希💕 文章目录一、前言二、无参构造&析构三、基础接口1.empty和clear2.size和capacity3.[]和iterator四、reserve和resize五、尾插尾删六、其他构造1.迭代器区间构造2.拷贝构造七、memcpy问题八、完整代码一、前言 在模拟实现容器时候࿰…...
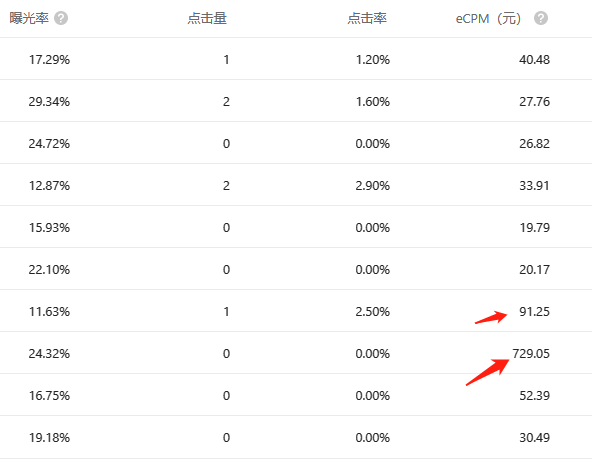
微信小程序、小游戏的流量主一般可以赚多少钱?
本篇文章主要科普小程序、小游戏流量主一般赚钱的实际情况,通过在下长期运营的经验汇总而成。 日期:2023年2月26日 作者:任聪聪 小程序、小程序满1000用户后即可开通流量主,但实际上很多人并没有传说中的那种日赚几千的流量收入的…...
jni-Demo-基于linux(c++ java)
跑一个jni 的最简单的Demo需要提前准备 VsCode 编译器、win10下,vscode中集成linux操作系统、c编译器(gcc、g),java编译器(jdk1.8)参考:https://mangocool.com/1653030123842.htmlJniDemo类&…...
指针的进阶——(1)
本次讲解重点: 1、字符指针 2、数组指针 3、指针数组 4、数组传参和指针传参 5、函数指针 关于指针这个知识点的主题,我们在前面已经初级阶段已经对指针有了大致的理解和应用了。我们知道了指针的概念: 1、指针就是地址,但口…...

电商平台的促销活动如何抵御大流量的ddos攻击
每一次活动大促带来的迅猛流量,对技术人而言都是一次严峻考验。如果在活动期间遭受黑产恶意 DDoS 攻击,无疑是雪上加霜。电商的特性是业务常态下通常不会遭受大流量 DDoS 攻击,且对延迟敏感,因此只需要在活动期间按需使用 DDoS 防…...

代码随想录-48-104. 二叉树的最大深度
目录前言题目1.层序迭代思路2. 本题思路分析:3. 算法实现4. pop函数的算法复杂度5. 算法坑点前言 在本科毕设结束后,我开始刷卡哥的“代码随想录”,每天一节。自己的总结笔记均会放在“算法刷题-代码随想录”该专栏下。 代码随想录此题链接 …...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
