算法模板之单调栈解密 | 图文详解

🌈个人主页:聆风吟
🔥系列专栏:算法模板、数据结构
🔖少年有梦不应止于心动,更要付诸行动。
文章目录
- 📋前言
- 一. ⛳️单调栈讲解
- 1.1 🔔单调栈的定义
- 1.2 🔔如何维护一个单调栈
- 1.3 🔔单调栈的用途
- 1.4 🌟模板总结(重点)🌟
- 1.4 🔔单调栈的实例练习
- 📝全文总结
📋前言
💬 hello! 各位铁子们大家好哇,今天作者给大家带来了单调栈的算法解密,因为前面我们已经讲解了用数组模拟栈过程,今天单调栈也是采用数组模拟,在此就不多做叙述有需要补漏的小伙伴可以自行前往下面专栏去浏览。
📚 系列专栏:本期文章收录在《算法模板》,大家有兴趣可以浏览和关注,后面将会有更多精彩内容!
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
一. ⛳️单调栈讲解
1.1 🔔单调栈的定义
定义:栈内的元素是单调递增或单调递减的栈。
1.2 🔔如何维护一个单调栈
- 单调递增栈:在保持栈内元素单调递增的前提下,如果栈顶元素大于要入栈的元素,将栈顶元素弹出,将新元素入栈。
- 单调递减栈:在保持栈内元素单调递减的前提下,如果栈顶元素小于要入栈的元素,则将栈顶元素弹出,将新元素入栈。
1.3 🔔单调栈的用途

由上图可以看出,对于栈内元素来说:
- 在栈内左边的数就是数组中左边第一个比自己小的元素;
- 但元素被弹出时,遇到的就是数组中右边第一个比自己小的元素。
对于将要入栈的元素来说:在对栈进行更新后(即弹出了所有比自己大的元素),此时栈顶元素就是数组中左侧第一个比自己小的元素;

由上图可以看出,对于栈内元素来说:
- 在栈内左边的数就是数组中左边第一个比自己大的元素;
- 但元素被弹出时,遇到的就是数组中右边第一个比自己大的元素。
对于将要入栈的元素来说:在对栈进行更新后(即弹出了所有比自己小的元素),此时栈顶元素就是数组中左侧第一个比自己大的元素;
由此,我们可以看出单调栈的用途是:给定一个序列,指定一个序列中的元素,求解该元素左侧或右侧第一个比自己小或大的元素。
1.4 🌟模板总结(重点)🌟
本文总结的模板是找出每个数左边离它最近的比它大或小的数,右边的可以自行推导(单看模板比较抽象,建议看完下面的题目,在返回来看)
//常见模型:找出每个数左边离它最近的比它大/小的数
int tt = 0;//栈顶指针
for (int i = 1; i <= n; i ++ )
{//check函数是判断查找://1. 每个数左边第一个比它小的数//2. 还是每个数左边第一个比它大的数while (tt && check(stk[tt], i)) tt -- ;stk[ ++ tt] = i;
}
1.4 🔔单调栈的实例练习
⌈ 在线OJ链接 ⌋
题目:

输入样例:
5
3 4 2 7 5
输出样例:
-1 3 -1 2 2
解题思路:
我们还是以上面的 3 4 2 7 5 来举例分析,开始遍历 3 这个元素,此时栈为空,那就表明 3 这个元素左侧没有比自身小的元素,将结果 -1 记录一下(或者直接输出)。然后将 3 压入栈中。遍历到 4 时发现 4 大于栈顶的元素 3,表明 4 这个元素左侧第一个比自身小的元素是 3,将结果 3 记录一下(或者直接输出)。遍历到 2 时,发现 2 小于栈顶的元素 4,4 是不可能作为结果输出的,所以需要将栈顶的 4 弹出。弹出之后栈顶的元素就是 3 ,同样 2 仍然小于 3,需要再次将 3 弹出。此时我们发现栈里面已经没有元素了,说明 2 的左侧没有比自身小的元素,将结果 -1 记录一下。然后将 2 压入栈中。其他的元素同理便可以得出,下面给出了动图,这里就不一一讲解了!
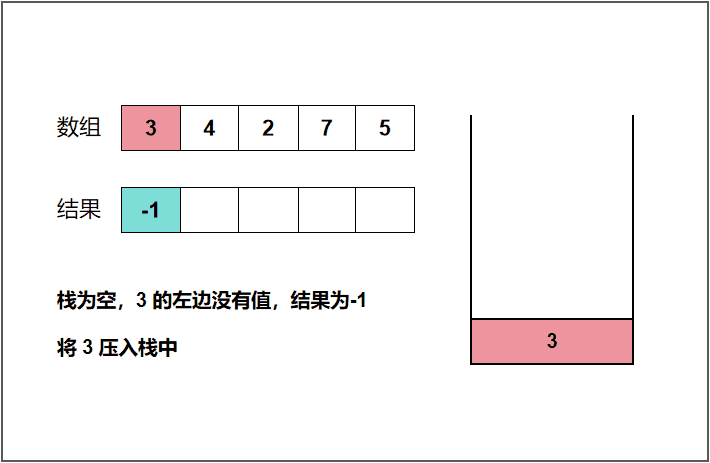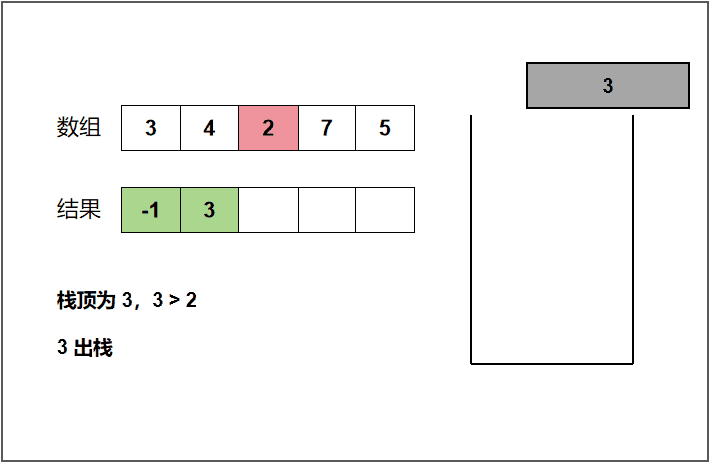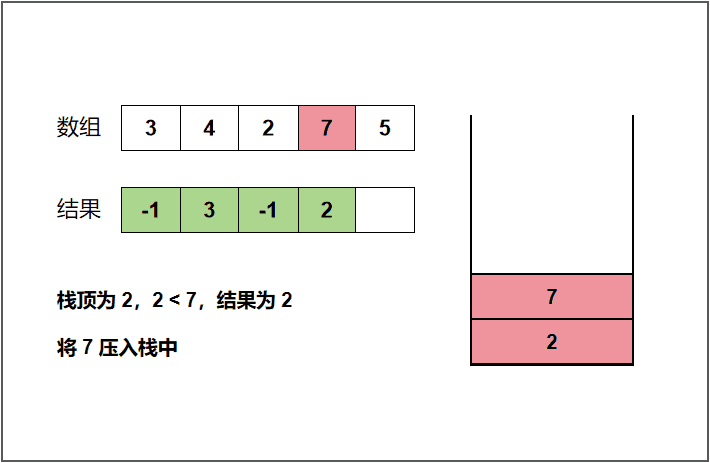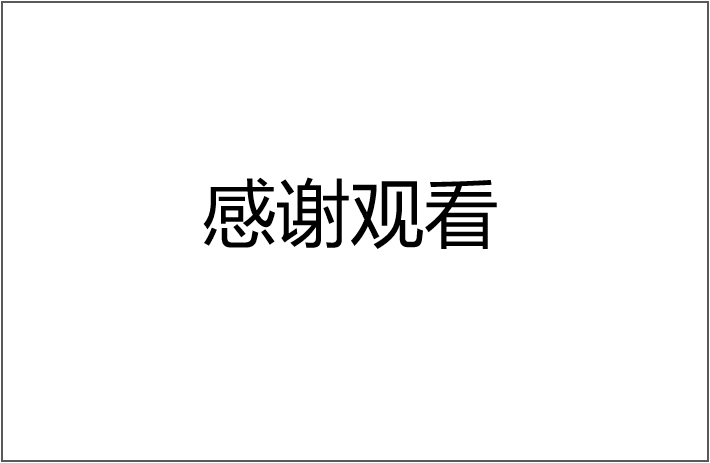
c++代码:
#include <iostream>using namespace std;
const int N = 100010;
int stk[N], tt;int main()
{int n = 0;cin >> n;for(int i = 0; i < n; i++){int x = 0;cin >> x;//如果栈顶元素大于当前待入栈元素,则出栈while(tt && stk[tt] >= x) tt--;if(tt){//栈顶元素就是左侧第一个比它小的元素。cout << stk[tt] << " ";}else {//如果栈空,则没有比该元素小的值。cout << "-1" << " ";}//将当前元素加入单调栈中stk[++tt] = x;}return 0;
}
📝全文总结
本文主要讲解:
- 单调栈的定义:栈内的元素是单调递增或单调递减的栈;
- 如何维护一个单调栈;
- 单调栈的用途:给定一个序列,指定一个序列中的元素,求解该元素左侧或右侧第一个比自己小或大的元素;
- 实例练习
文章可能会有出现错误的地方,欢迎大家在评论区里指正,非常感谢。同时希望大家课下能够多敲多练,孰能生巧。
今天的内容就到这里了,你对今天的内容是否有所掌握?如果还有疑问的话请在评论区里多多提问,大家可以一起帮你解决,让我们共同进步。创作不易,如果对你有用的的话点个赞支持下作者,你们的支持是作者创作最大的动力。关注我不迷路,让我们下期再见✋✋。
相关文章:

算法模板之单调栈解密 | 图文详解
🌈个人主页:聆风吟 🔥系列专栏:算法模板、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️单调栈讲解1.1 🔔单调栈的定义1.2 🔔如何维护一个单…...

187.重复的 DNA 序列
题目来源: leetcode题目,网址:187. 重复的DNA序列 - 力扣(LeetCode) 解题思路: 使用两个哈希表,一个存放已遍历过的长度为 10 的字符串,另一个存放重复的长度为 10 的字符串。顺…...
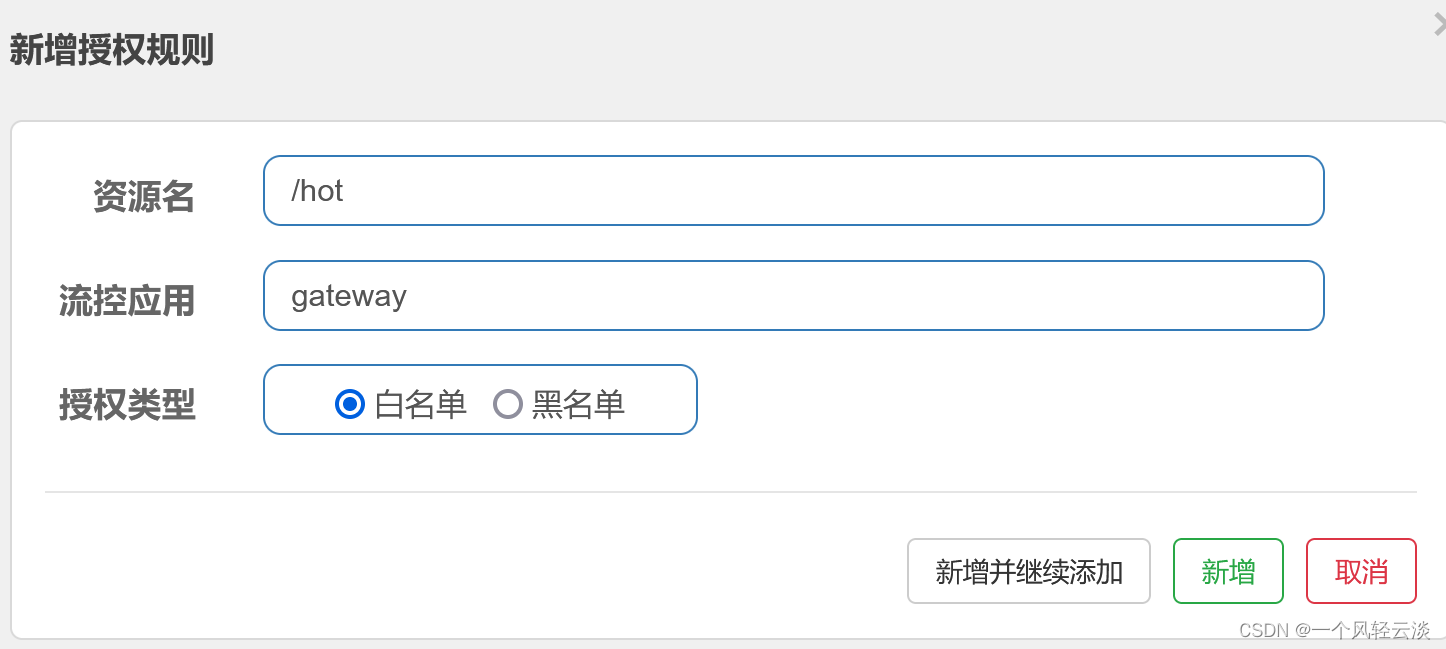
Sentinel黑白名单授权规则解读
目录 基本介绍 代码实战 架构说明 RequestOriginParser的实现类 网关添加请求头 配置授权规则 基本介绍 授权规则可以对请求方来源做判断和控制。 很多时候,我们需要根据调用来源来判断该次请求是否允许放行,这时候可以使用 Sentinel 的来源…...
)
Spring底层原理学习笔记--第二讲--(BeanFactory实现与ApplicaitonContext实现)
BeanFactory实现 package com.lucifer.itheima.a02;import lombok.extern.slf4j.Slf4j; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.beans.factory.config.BeanFactoryPostProcessor; import org.springframework.beans.fac…...
)
云原生|kubernetes |kubelet服务加入系统守护进程supervisor(centos7系统下演示通过)
前言: kubelet 是 Kubernetes 集群中的一个重要组件,运行在每个节点上,负责管理该节点上的容器和Pod。它与控制平面(如 API Server 和 kube-controller-manager)通信,确保节点上的容器与期望的状态保持一致…...

onnx 模型加载部署运行方式
1.通过文件路径的onnx模型加载方式: 在onnxruntime下面的主要函数:session Ort::Session(env, w_modelPath.c_str(), sessionOptions); 这里的文件路径是宽字节的,通过onnx文件路径直接加载模型。 在opencv下使用dnn加载onnx模型的主要函数: std::string model…...
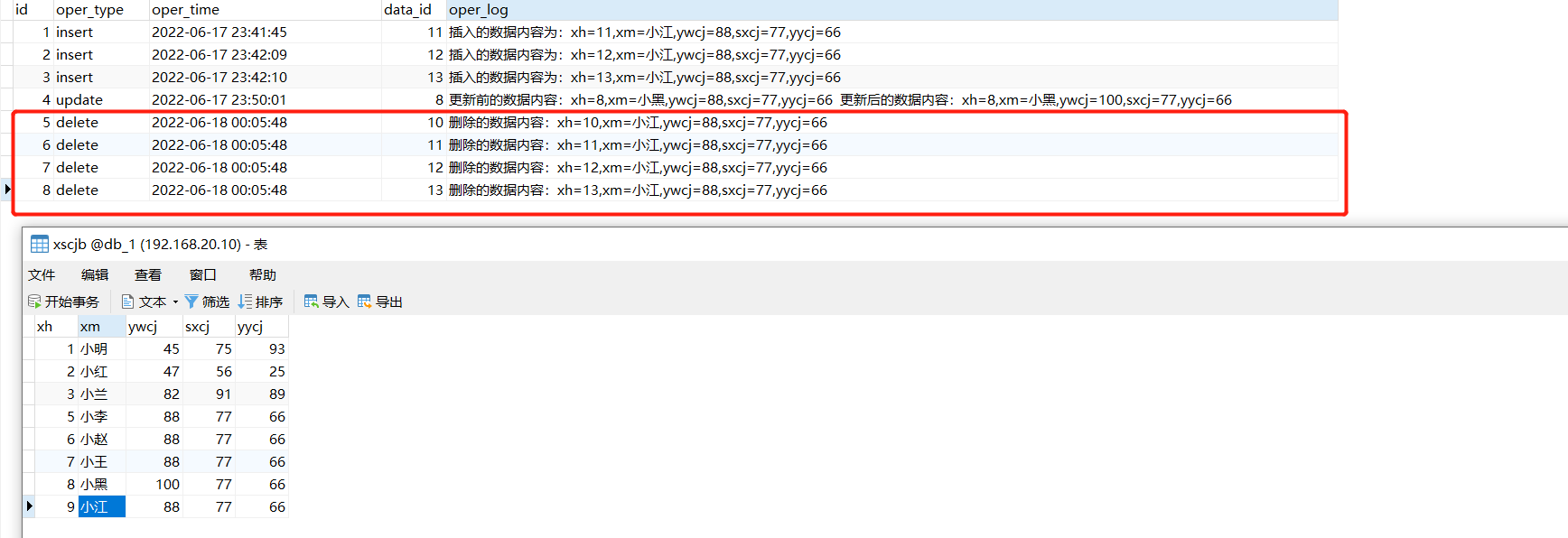
第68讲:MySQL触发器的核心概念以及常见的触发类型应用案例
文章目录 1.触发器的概念2.触发器操作的语法结构3.各类触发器的典型应用案例3.1.需求描述以及实现思路3.2.创建日志表3.3.INSERT类型的触发器3.4.UPDATE类型的触发器3.5.DELETE类型的触发器 1.触发器的概念 触发器是与表中数据相关的数据库对象,当表中的数据产生in…...
VS Code 开发 Spring Boot 类型的项目
在VS Code中开发Spring Boot的项目, 可以导入如下的扩展: Spring Boot ToolsSpring InitializrSpring Boot Dashboard 比较建议的方式是安装Spring Boot Extension Pack, 这里面就包含了上面的扩展。 安装方式就是在扩展查找 “Spring Boot…...

数据中心加密:保障数据安全的重要一环
随着信息化的快速发展,数据已经成为企业的重要资产,数据安全也成为了企业面临的重大挑战。数据中心作为企业数据存储和管理的重要场所,其安全性对于整个企业的数据安全具有至关重要的作用。而数据中心加密则是保障数据安全的重要一环。本文将…...

分享90个节日庆典PPT,总有一款适合您
分享90个节日庆典PPT,总有一款适合您 PPT下载链接:百度网盘 请输入提取码 提取码:8888 Python采集代码下载链接:采集代码.zip - 蓝奏云 学习知识费力气,收集整理更不易。知识付费甚欢喜,为咱码农谋福利…...
Python Faker批量生成测试数据
一、前言 在做自动化测试或压力测试时会需要大批量生成测试数据,简单的方式你可以写一个存储过程使用随机函数来生成记录,但这种生成数据看起来不够真实,其实有蛮多现成的工具可以完成这一任务。 二、Faker基本使用介绍 faker是一个生成伪…...

Docker-compose 运行MySQL 连接不上
Docker-compose 运行MySQL 连接不上 📔 千寻简笔记介绍 千寻简笔记已开源,Gitee与GitHub搜索chihiro-notes,包含笔记源文件.md,以及PDF版本方便阅读,且是用了精美主题,阅读体验更佳,如果文章对你有帮助请帮我点一个Star~ 更新:支持在线阅读文章,根据发布日期分类…...
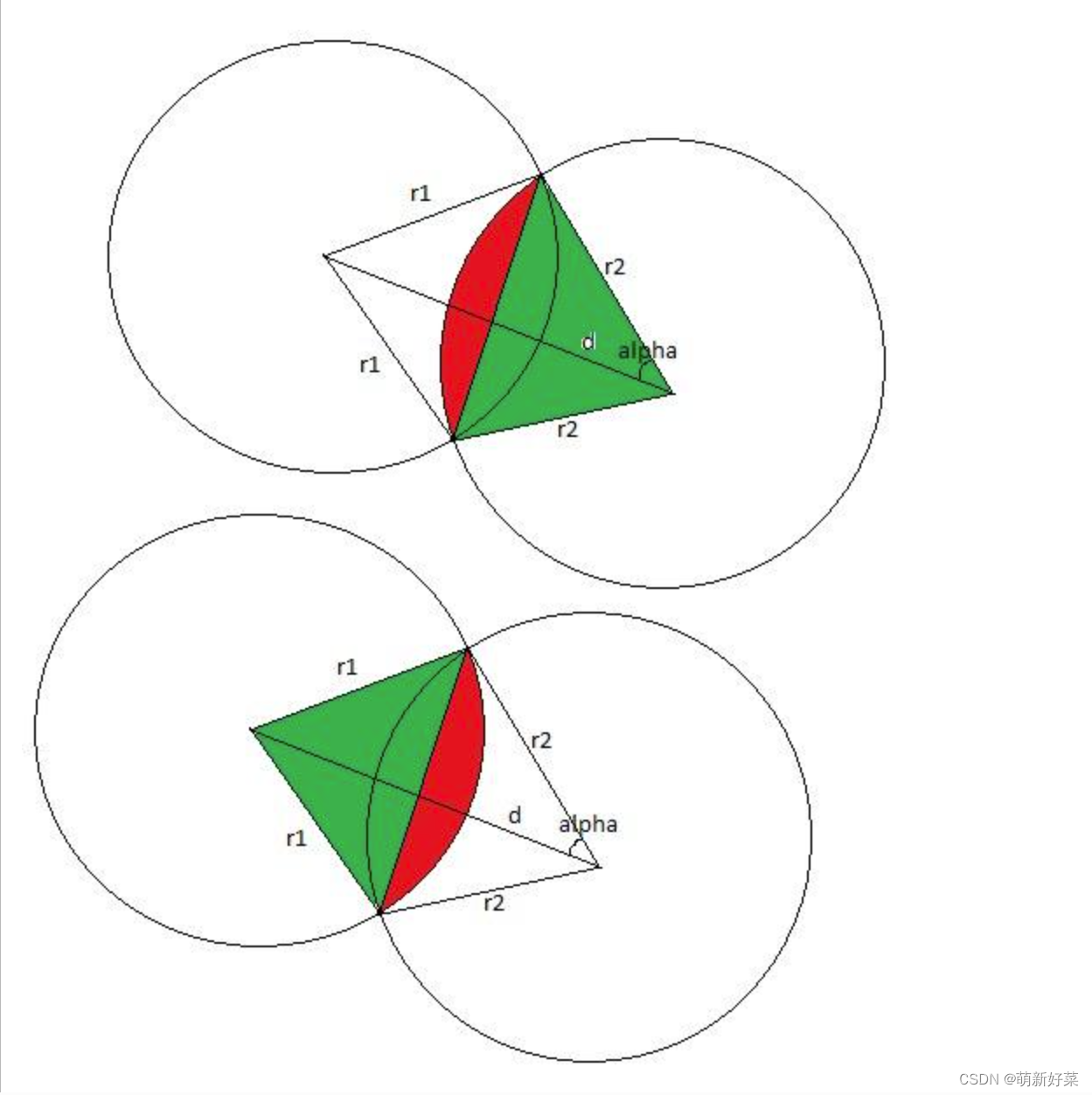
Educational Codeforces Round 2 D 计算几何
题目链接:Educational Codeforces Round 2 D 题目 给你两个圆。求它们相交处的面积。 输入 第一行包含三个整数 x1, y1, r1 ( - 109 ≤ x1, y1 ≤ 109, 1 ≤ r1 ≤ 109 ) - 第一个圆的圆心位置和半径。 第二行包含三个整数 x2, y2, r2 ( …...

hexo博客发布换电脑换地方了怎么办?
假如你有2台MacBook,一台在家,一台在公司。在家的hexo本地环境都搭好了,markdown文件等等也都放在本地source下的_posts文件夹里了。但是我过2天又想有个新文章发布,这时候电脑在公司,那么该怎么办? 把家里…...
最新知识付费变现小程序源码/独立后台知识付费小程序源码/修复登录接口
最新知识付费变现小程序源码,独立后台知识付费小程序源码,最新版修复登录接口。 主要功能 会员系统,用户登录/注册购买记录 收藏记录 基本设置 后台控制导航颜色 字体颜色 标题等设置 流量主广告开关小程序广告显示隐藏 广告主审核过审核…...
奥威BI软件 | 职场人的数据可视化救星
对时间紧张、工作繁重的职场人来说,一款易学易用、效率高、数据展现直观的数据可视化软件必不可少。奥威BI软件就是这样一款数据可视化软件,零编程开发报表,不需要额外多花时间,即可点击、拖拉拽完成数据分析、报表制作࿰…...

最长公共前缀[简单]
优质博文:IT-BLOG-CN 一、题目 编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀,返回空字符串""。 示例 1: 输入:strs ["flower","flow","flight"] 输出…...
-- Mysql8的详细安装与环境配置)
Java后端开发(十一)-- Mysql8的详细安装与环境配置
目录 1. mysql数据库下载 官网在线下载 2. 下载 MySQL的安装包 3. 安装MySQL...

什么是Spring?什么是IOC?什么是DI?IOC和DI的关系? —— 零基础可无压力学习,带源码
🧸欢迎来到dream_ready的博客,📜相信您对这几篇博客也感兴趣o (ˉ▽ˉ;) 📜什么是SpringMVC?简单好理解!什么是应用分层?SpringMVC与应用分层的关系? 什么是三层架构&…...
 和 gradient accumulated)
PyTorch 从tensor.grad 看 backward(权重参数) 和 gradient accumulated
1. 新建一个自变量 tensor x import torchx torch.ones(1, requires_gradTrue) print(x)1. 输出: tensor([1.], requires_gradTrue)2. 写一个 forward import torchx torch.ones(1, requires_gradTrue) y x**2 z x**33. y, z 都 backward import torchx to…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
