Docker-compose 运行MySQL 连接不上
Docker-compose 运行MySQL 连接不上
📔 千寻简笔记介绍
千寻简笔记已开源,Gitee与GitHub搜索chihiro-notes,包含笔记源文件.md,以及PDF版本方便阅读,且是用了精美主题,阅读体验更佳,如果文章对你有帮助请帮我点一个Star~
更新:支持在线阅读文章,根据发布日期分类。
文章目录
- Docker-compose 运行MySQL 连接不上
- 📔 千寻简笔记介绍
- 简介
- 本文关键词
- 实现步骤
- 1 重新分配权限
简介
在服务器部署 mysql 遇到了一个问题,起初根据文档去启动 MySQL,正常启动后发现,远程连接不上,起初怀疑是服务器防护墙没关,后来我把服务器防火墙关闭以及放行云服务器厂商的防火墙,还是连接不上 MySQL,但是在容器内部是可以进入的,后来我去查看容器的启动日志发现,日志打印了一个警告。<
相关文章:

Docker-compose 运行MySQL 连接不上
Docker-compose 运行MySQL 连接不上 📔 千寻简笔记介绍 千寻简笔记已开源,Gitee与GitHub搜索chihiro-notes,包含笔记源文件.md,以及PDF版本方便阅读,且是用了精美主题,阅读体验更佳,如果文章对你有帮助请帮我点一个Star~ 更新:支持在线阅读文章,根据发布日期分类…...
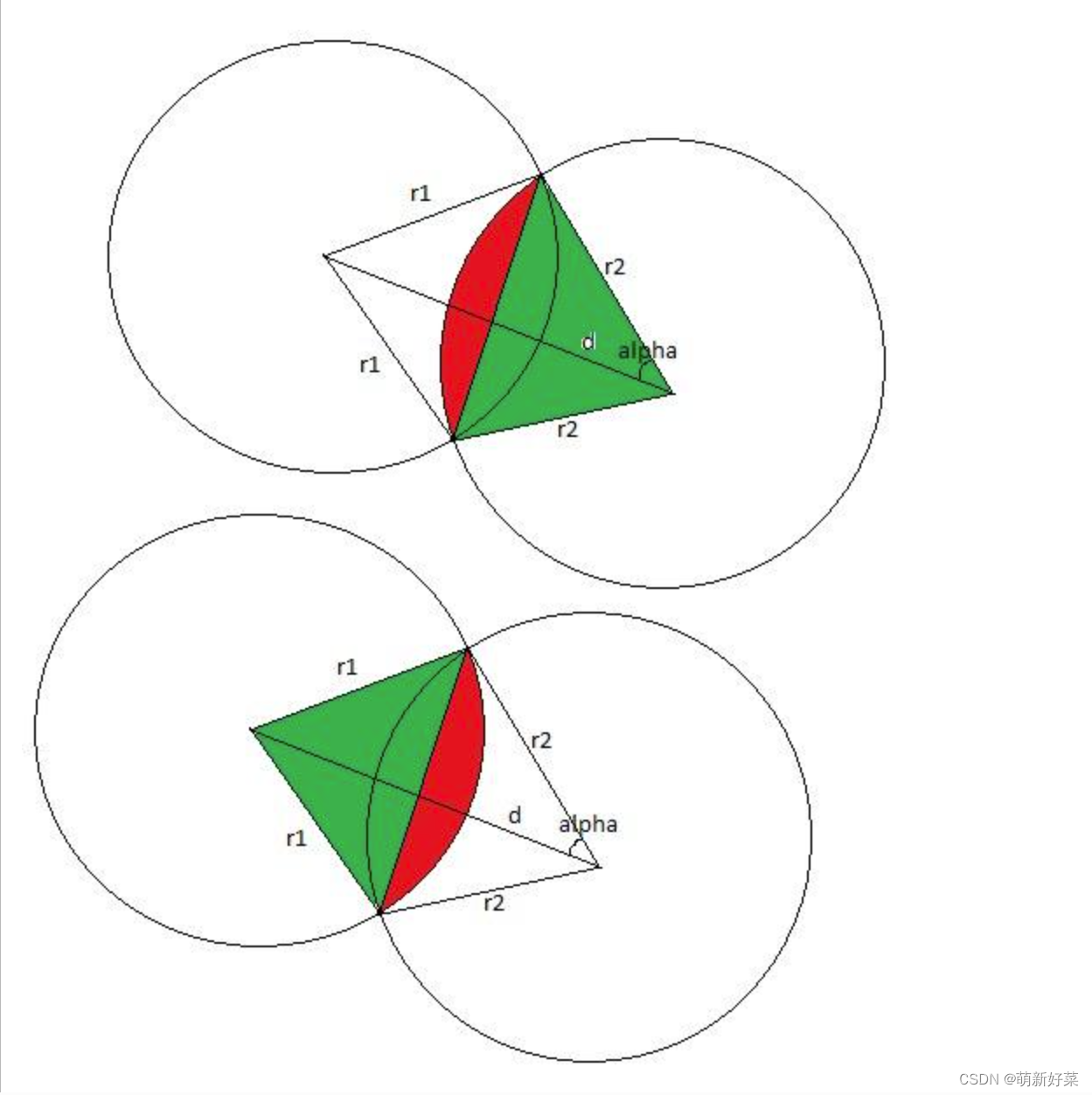
Educational Codeforces Round 2 D 计算几何
题目链接:Educational Codeforces Round 2 D 题目 给你两个圆。求它们相交处的面积。 输入 第一行包含三个整数 x1, y1, r1 ( - 109 ≤ x1, y1 ≤ 109, 1 ≤ r1 ≤ 109 ) - 第一个圆的圆心位置和半径。 第二行包含三个整数 x2, y2, r2 ( …...

hexo博客发布换电脑换地方了怎么办?
假如你有2台MacBook,一台在家,一台在公司。在家的hexo本地环境都搭好了,markdown文件等等也都放在本地source下的_posts文件夹里了。但是我过2天又想有个新文章发布,这时候电脑在公司,那么该怎么办? 把家里…...
最新知识付费变现小程序源码/独立后台知识付费小程序源码/修复登录接口
最新知识付费变现小程序源码,独立后台知识付费小程序源码,最新版修复登录接口。 主要功能 会员系统,用户登录/注册购买记录 收藏记录 基本设置 后台控制导航颜色 字体颜色 标题等设置 流量主广告开关小程序广告显示隐藏 广告主审核过审核…...
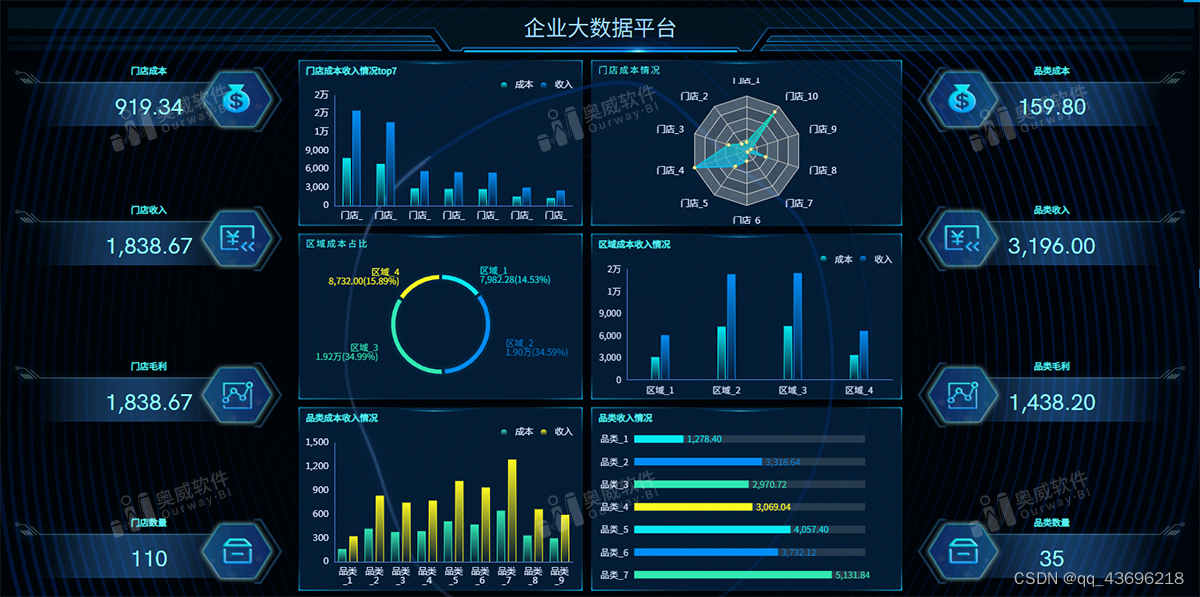
奥威BI软件 | 职场人的数据可视化救星
对时间紧张、工作繁重的职场人来说,一款易学易用、效率高、数据展现直观的数据可视化软件必不可少。奥威BI软件就是这样一款数据可视化软件,零编程开发报表,不需要额外多花时间,即可点击、拖拉拽完成数据分析、报表制作࿰…...

最长公共前缀[简单]
优质博文:IT-BLOG-CN 一、题目 编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀,返回空字符串""。 示例 1: 输入:strs ["flower","flow","flight"] 输出…...
-- Mysql8的详细安装与环境配置)
Java后端开发(十一)-- Mysql8的详细安装与环境配置
目录 1. mysql数据库下载 官网在线下载 2. 下载 MySQL的安装包 3. 安装MySQL...

什么是Spring?什么是IOC?什么是DI?IOC和DI的关系? —— 零基础可无压力学习,带源码
🧸欢迎来到dream_ready的博客,📜相信您对这几篇博客也感兴趣o (ˉ▽ˉ;) 📜什么是SpringMVC?简单好理解!什么是应用分层?SpringMVC与应用分层的关系? 什么是三层架构&…...
 和 gradient accumulated)
PyTorch 从tensor.grad 看 backward(权重参数) 和 gradient accumulated
1. 新建一个自变量 tensor x import torchx torch.ones(1, requires_gradTrue) print(x)1. 输出: tensor([1.], requires_gradTrue)2. 写一个 forward import torchx torch.ones(1, requires_gradTrue) y x**2 z x**33. y, z 都 backward import torchx to…...

fedora 命令行代理proxychains 使用flatpak下载 flathub包
feodra 28 有 tsocks - (rpm 包)工具, 后面就没有了. 不过还有替代工具 proxychains 当前操作环境 Fedora 38 proxychains 配置文件所在位置 # 全局配置 /etc/proxychains.confproxychains looks for configuration in the following order: SOCKS5 proxy port in environme…...

介绍kamailio的dialog模块
# 介绍kamailio的dialog模块 kamailio的dialog模块一般有四个作用: - 读写对话变量 - 跟uac模块配合,完成uac trunk auth功能 - 统计early_dialogs和active_dialogs等 - 利用dialog profile实现分类统计功能或者实现呼叫限制功能 dialog模块的参数可以…...
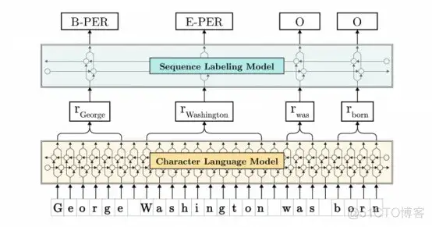
性能优于BERT的FLAIR:一篇文章入门Flair模型
文章目录 What is FLAIR?FLAIR ModelContextual String Embedding for Sequence Labelingexample FLAIR Application AreaSentiment AnalysisNamed Entity RecognitionText Classification FLAIR一、什么是FLAIR?二、FLAIR Library的优势是什么ÿ…...
Weblogic ssrf漏洞复现
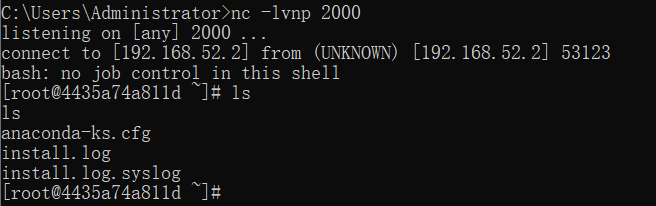
文章目录 一、漏洞描述二、漏洞特征1.查看uddiexplorer应用2.漏洞点 三、漏洞复现1.获取容器内网ip2.VULHUB Weblogic SSRF漏洞 docker中 centos6 无法启动的解决办法3.准备payload4.反弹shell 一、漏洞描述 SSRF 服务端请求伪造(Server-Side Request Forgery),是一种由攻击者…...
Memcached构建缓存服务器
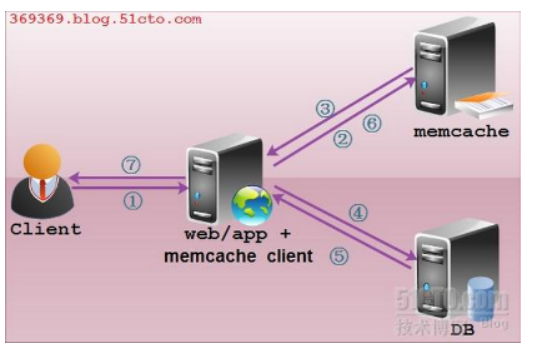
Memcache介绍 1、特点 内置存储方式----------为了提高性能,memcached中保存的数据都存储在memcache内置的内存存储空间中。由于数据仅存在于内存中,重启操作系统会导致全部数据消失 简单key/value存储--------------服务器不关心数据本身的意义及结构&…...
vue3+element Plus实现弹框的拖拽、可点击底层页面功能
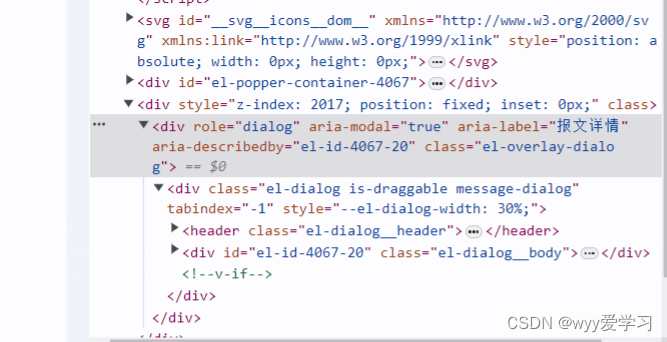
1、template部分 <el-dialog:modal"false"v-model"dialogVisible"title""width"30%"draggable:close-on-click-modal"false"class"message-dialog"> </el-dialog> 必须加的属性 modal:是否去掉遮罩层…...
)
Vue+elementui 纯前端实现Excel导入导出功能(区分表头标题)
引入插件 import * as XLSX from "xlsx/xlsx.mjs"; import { read, utils } from xlsx/xlsx.mjs; 上传文件方法 // 上传文件状态改变时的钩子,添加文件、上传成功和上传失败时都会被调用async handle(ev) {//改变表格key值this.$refs.cpkTable.loading…...

使用Scrapy的调试工具和日志系统定位并解决爬虫问题
目录 摘要 一、Scrapy简介 二、Scrapy的调试工具 1、Shell调试工具 2、断点调试 三、Scrapy的日志系统 四、实例解析 1、启用详细日志 2、断点调试 3、分析日志 4、解决问题 五、代码示例 总结 摘要 本文详细介绍了如何使用Scrapy的调试工具和日志系统来定位并解…...
Pycharm安装配置Pyqt5教程(保姆级)
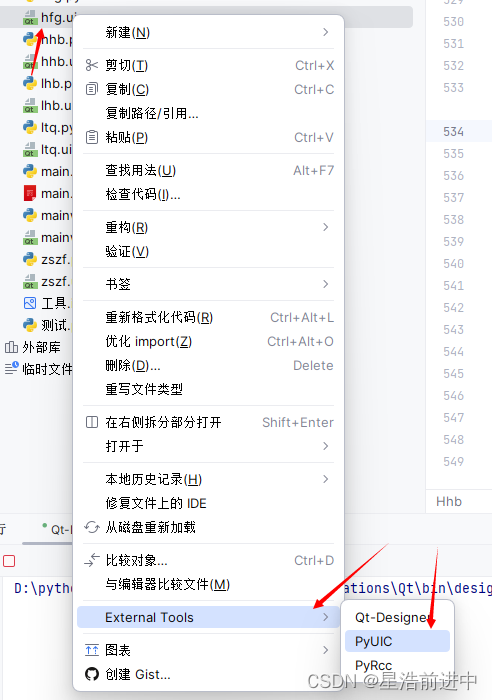
目录 一、前言 1、依赖包 2、工具 二、安装依赖包 三、配置环境 四、配置设计工具 1、Qt Designer 2、PyRcc 3、PyUIC 五、使用 1、界面设计 2、ui文件转化为py文件 一、前言 很多情况下需要为程序设计一个GUI界面,在Python中使用较多的用户界面设计工具…...
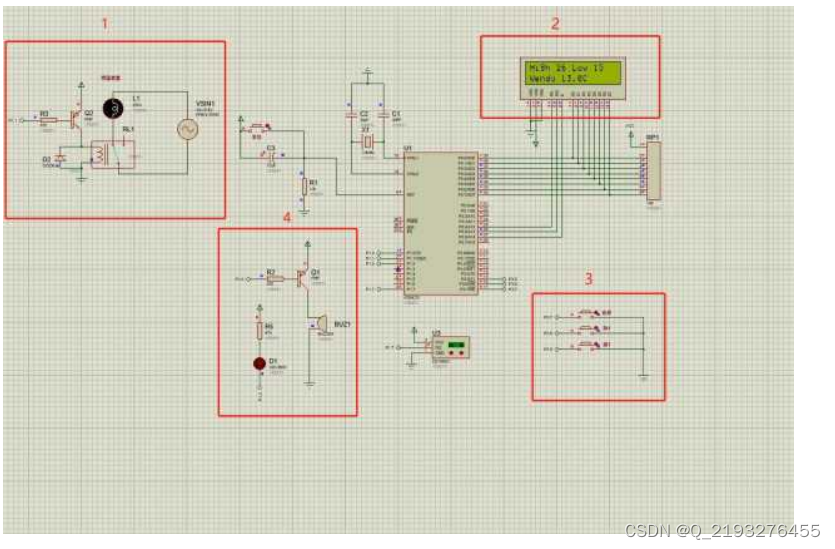
基于单片机的养殖场温度控制系统设计
博主主页:单片机辅导设计 博主简介:专注单片机技术领域和毕业设计项目。 主要内容:毕业设计、简历模板、学习资料、技术咨询。 文章目录 主要介绍一、控制系统设计二、系统方案设计2.1 系统运行方案设计2.1.1 羊舍环境温度的确定 三、 系统仿…...
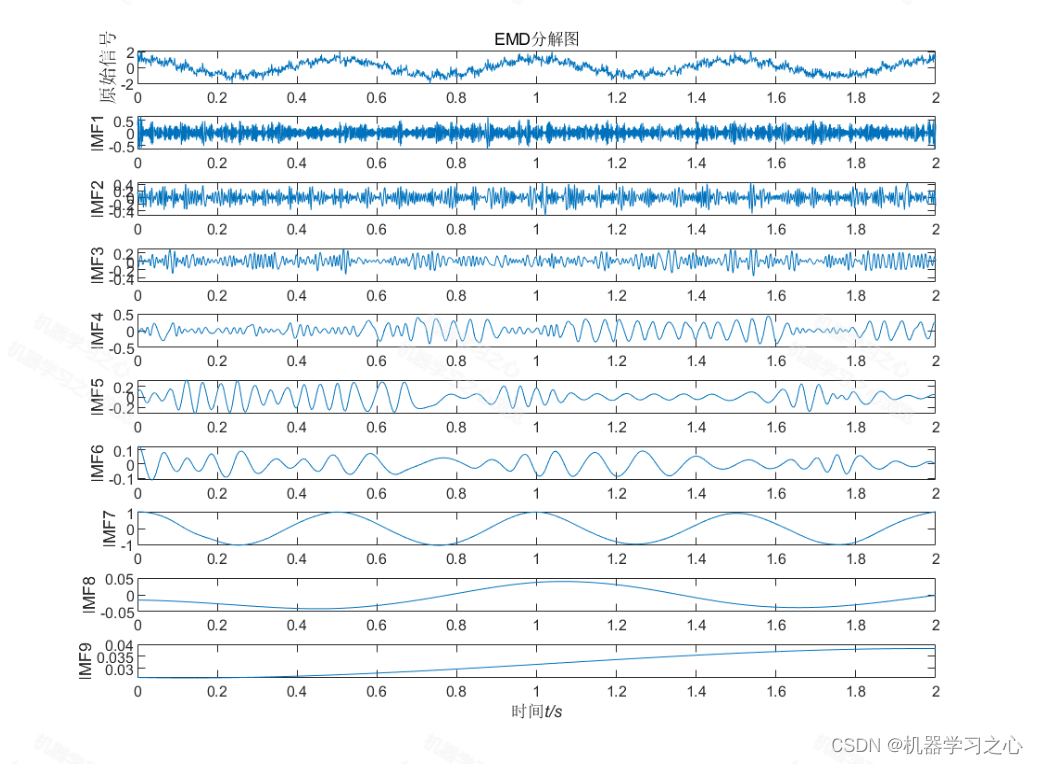
时序分解 | Matlab实现EMD经验模态分解时间序列信号分解
时序分解 | Matlab实现EMD经验模态分解时间序列信号分解 目录 时序分解 | Matlab实现EMD经验模态分解时间序列信号分解效果一览基本介绍程序设计参考资料 效果一览 基本介绍 Matlab实现EMD经验模态分解时间序列信号分解 Matlab语言 算法新颖小众,用的人很少…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
