03 贝尔曼公式
贝尔曼公式
- 前言
- 1、Motivating examples
- 2、state value
- 3、Bellman equation:Derivation
- 4、Bellman equation:Matrix-vector form
- 4、Bellman equation:Solve the state value
- 5、Action value
前言
本文来自西湖大学赵世钰老师的B站视频。本节课主要介绍贝尔曼公式。
本节课概要:本节课需要抓住两个内容,state value 和 the Bellman equation。本次大纲如下:

1、Motivating examples

return就是有多条轨迹,沿着这些轨迹可以得到很多的rewards,把这些rewards求和,就得到return。为什么return这么重要呢?通过上图三个例子来做介绍,上面三幅图的环境是一样的,s4是目标,s2是forbidden area,白色的是accessible area。这三幅图不同的是在状态s1上的策略是不同的,第一幅图在s1会往下走,第二幅图在s1会往右走,第三幅图在s1有50%的概率往下走,50%的概率往右走,在其他位置上,它们的策略是一样的。
因此,我们需要回答,从s1出发,哪一个策略是最好的,哪一个策略是最差的,从直观上来说,第一幅图的策略是最好的,第二幅图的策略是最差的,第三幅图的策略不好也不差。因为第一幅图从s1出发不会进入到forbidden area,第二幅图会直接进入forbidden area,第三幅图有50%的概率进入到forbidden area。那么我们可以用数学来描述这一种直观,数学工具就是这个return。return之所以重要,是因为它告诉我们哪个策略好,哪个策略坏,即它能够评估策略。
下面我们分别来计算这三个例子对应的return:
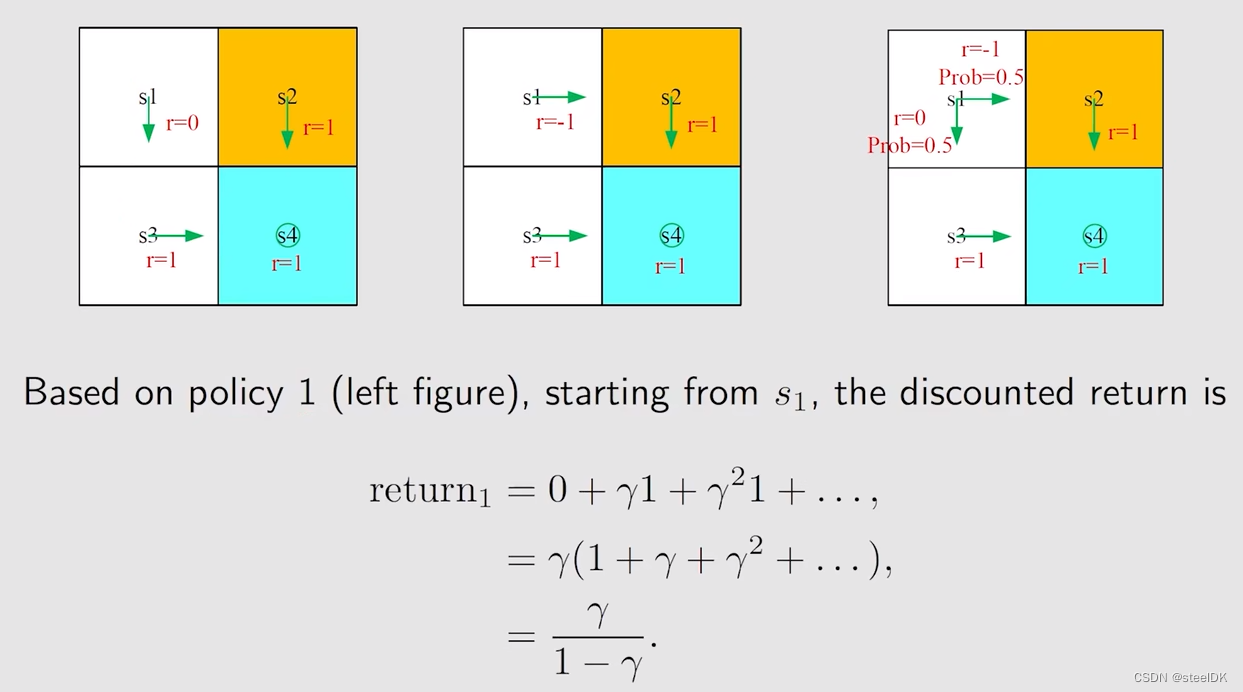
对于第一幅图,从s1到s3,得到的reward为0,从s3到s4得到的reward为γ乘以1,然后就会一直呆在s4,得到的结果如上图。同样的方法我们可以得到第二幅图和第三幅图对应的return。策略3对应的return实际上就是我们接下来要学的state value。


下面做个总结:
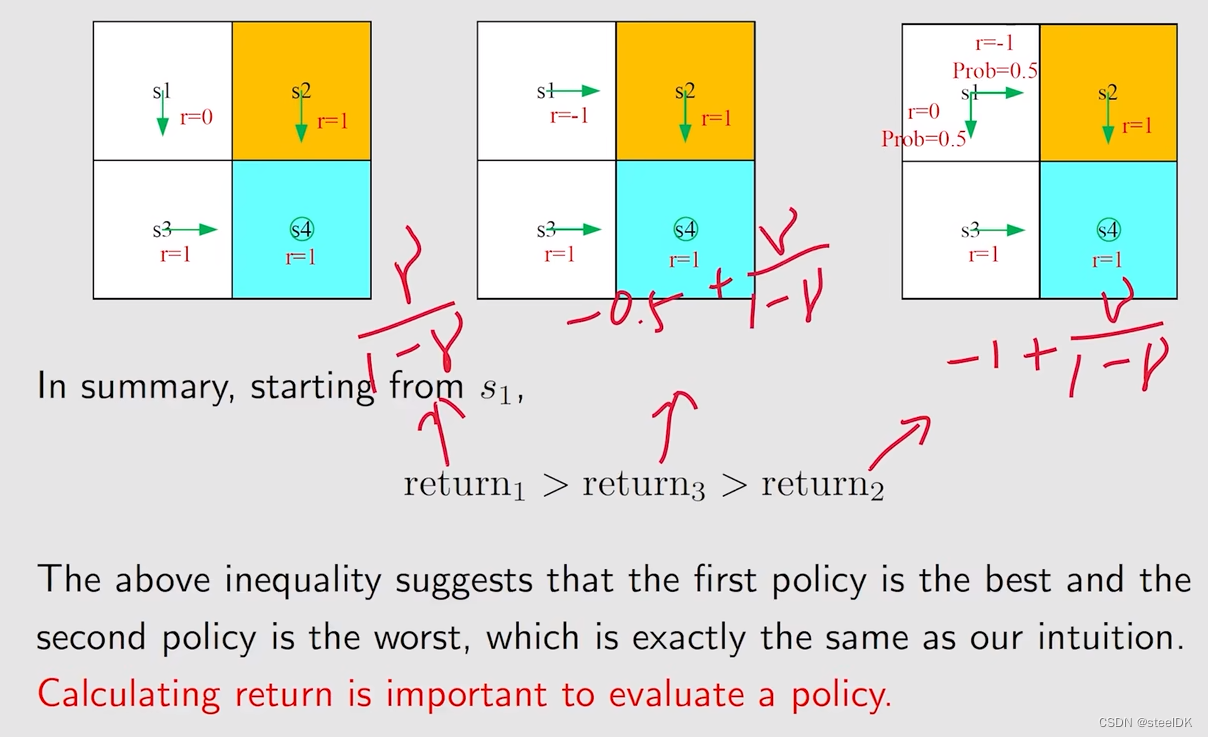
下面进一步来讲一下return如何计算。
考虑从不同状态出发,计算的return。用vi表示从状态si出发得到的return。有两种方法,第一种方法为:

第二种方法为:

v1就是从s1出发,到达s2之后,就相当于从s2出发了,从s2出发一定得到的是v2,因此v1可以写成上述形式,依次类推。
但同样也面临着一些问题,在计算时我们要求解v,但还得事先知道v,这个好像陷入了一个不可能解决的问题。看似好像无法解决,但如果我们用数学的话,就可以解决了,首先我们将上图中的式子写成矩阵和向量的形式:
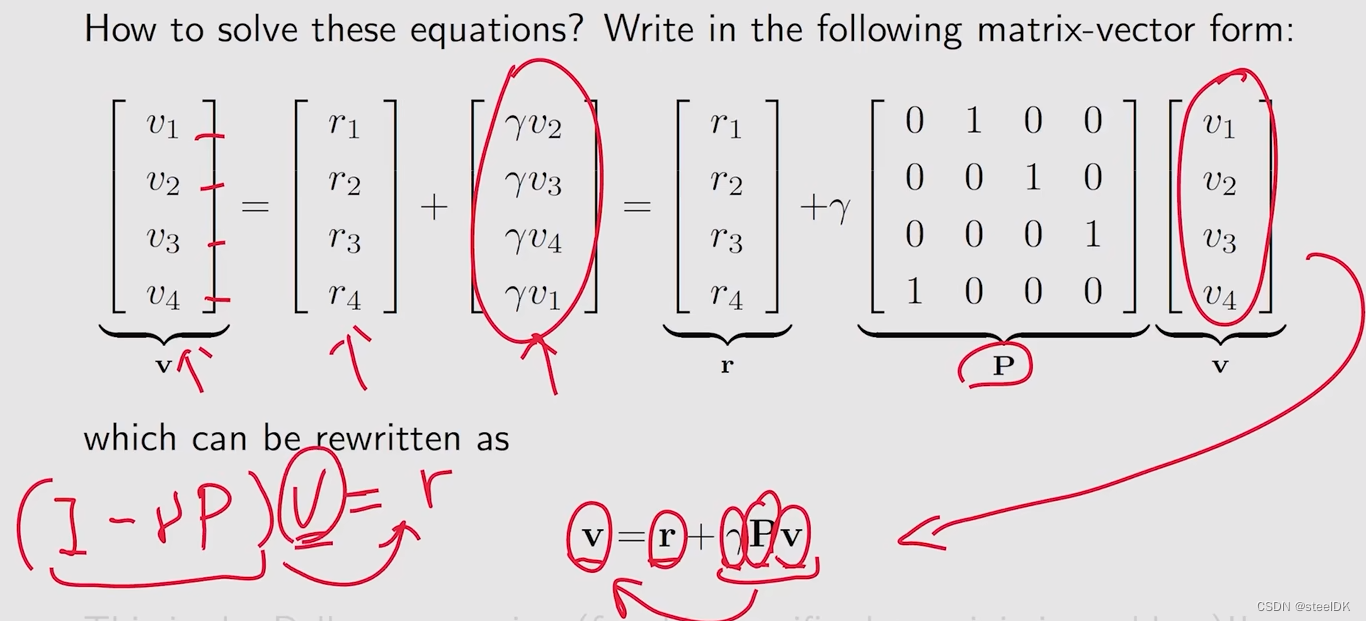

这是一个比较简单的,特别是针对确定性问题的贝尔曼公式,后面会更加正式地介绍一般化地贝尔曼公式。但这个公式也告诉我们,一个状态地value实际上依赖于其他状态地value,这个就是bootstrapping想法;另外就是matrix-vector form也是非常重要地,就是我们只看一个公式是没办法解决的,但我们把所有的公式全都组合到一起,得到一个matrix-vector form就很容易求出来。
下面我们在做一个例子来加深理解:

2、state value
这一部分介绍state value概念。为了介绍state value,我们首先引入一些符号:

首先看单步的,St是当前状态,在当前状态下采取的动作是At,得到的下一个reward是Rt+1,跳到下一个状态是St+1。t指的是当前时刻,t+1指的是下一时刻。

St、At、Rt+1都是随机变量,这也就意味着我们可以求解它们的期望。这样单步的过程可以推广到多步的trajectory。下图中的Gt也是一个随机变量。

有了以上基础,我们可以来定义state value了:
第一点:state value function 是关于状态s的函数,从不同的s出发,得到的轨迹不同,显然得到的discount return也不同,求平均也是不同的;第二点:state value function是一个策略的函数,显然不同的策略会得到不同的轨迹,不同的轨迹又会得到不同的return,进而会得到不同的state value。最后一点是,这个state value不仅仅是一个数值的value,它也代表一种价值,当一个state value比较大的时候,就代表这个状态是比较有价值的,因为从这个状态出发,我们会得到更多的return。
最后来回答这样一个问题:state value和return有什么区别?return是针对单个trajectory求的return,而state value是对多个trajectory得到的return再求平均值,如果我们从一个状态出发,有可能得到多个trajectory,此时return和state value是有区别的,但是如果我们从一个状态出发,一切都是确定性的,也就是说只能得到一条trajectory,此时从那个状态出发得到的return和state value是一样的。
下面我们来看一个例子:

上述三幅图分别对应三个策略,假设从左到右分别是π1、π2、π3,接下来我们计算在这三个不同策略下,同一个状态s1的state value。计算vπ1(s1)、vπ2(s1)、vπ3(s1)可知,第一幅图对应的策略是最好的。(上图所举例子是求确定性的trajectory下的state value)
3、Bellman equation:Derivation
我们首先来学习的是如何来推到贝尔曼公式。本小节重点如下:

总结:我们要学会用贝尔曼公式计算上节中提到的state value,贝尔曼公式用一句话可以概况来说就是它描述了不同状态的state value之间的关系。

首先考虑这样一个trajectory,从状态St出发,采取动作At,得到Rt+1和St+1,以此类推,得到了上图中的一个trajectory。这样的一个trajectory可以计算它的discounted return Gt,从上图推导后的公式来看,Gt就等于我立刻能得到的immediate reward Rt+1,再加上从下一时刻出发得到的Gt+1乘以discount rate γ。

从上图可以看出,state value可以用蓝色的两个期望来表示,分别计算这两个期望就能得到贝尔曼公式。下图就是第一个期望的计算方法:

第一项期望实际上就是immediate rewards的mean,第二项的期望公式见下图:

第二项是从当前状态s出发所得到的下一时刻的return的mean。从当前状态出发,可以有多个选择,可以跳到s撇,跳到不同s撇的概率是p(s撇|s),跳到s撇得到的期望值是E(Gt+1|St=s,St+1=s撇),E(Gt+1|St=s,St+1=s撇)指的是当前状态是s,下一时刻状态是s撇,计算从下一个状态出发,所得到的return的mean。E(Gt+1|St=s,St+1=s撇)中的St=s是可以去掉的,因为我已经知道了下一个状态是s撇,就不用关心之前是什么状态了。E(Gt+1|St+1=s撇)就是针对s撇的state value,用vπ(s撇)。从s到s撇的概率p(s撇|s)就是从状态s出发,选取不同的动作a的概率,乘以当前状态下采取动作a得到s撇的概率,不同动作a求和就是p(s撇|s)。
总之,第二个期望就是未来rewards的一个均值。
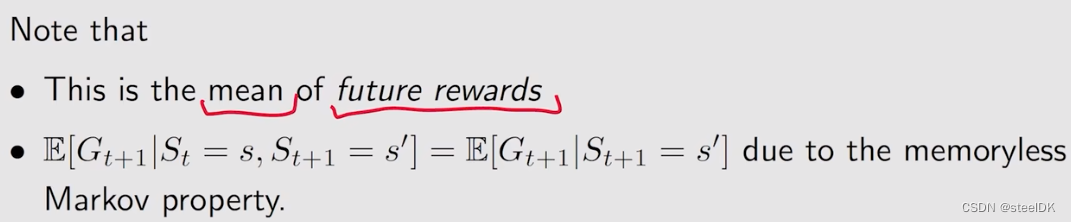
至此,我们就可以给出贝尔曼公式的表达式了:

上图中的公式就是贝尔曼公式,它实际上描述了不同状态的state value之间的关系。公式左边是s的state value,右边是s撇的state value。另外,这个式子包含两项,一项是immediate reward,另一项是future reward。上述式子应该是对状态空间中所有的状态都成立的,所以,如果我们有n个状态,我们就会有n个这样的式子,通过n个这样的式子,我们就可以把state value给求解出来,但我们通常就写上述一个式子,大家千万不要以为贝尔曼公式就只有这一个式子。

状态值如何计算呢?vπ(s)依赖于vπ(s撇),而vπ(s撇)又依赖于其它状态值,看起来似乎没办法计算,这其实就是bootstrapping,我们可以用矩阵来进行计算。另外,这个式子依赖于很多概率,π(a|s)是policy,贝尔曼公式是依赖于概率的,我们要把state value给计算出来,实际上我们现在正在做的事情就叫policy evaluation,就是去evaluation这个policy是好是坏。

上图中的绿色箭头就是策略π。

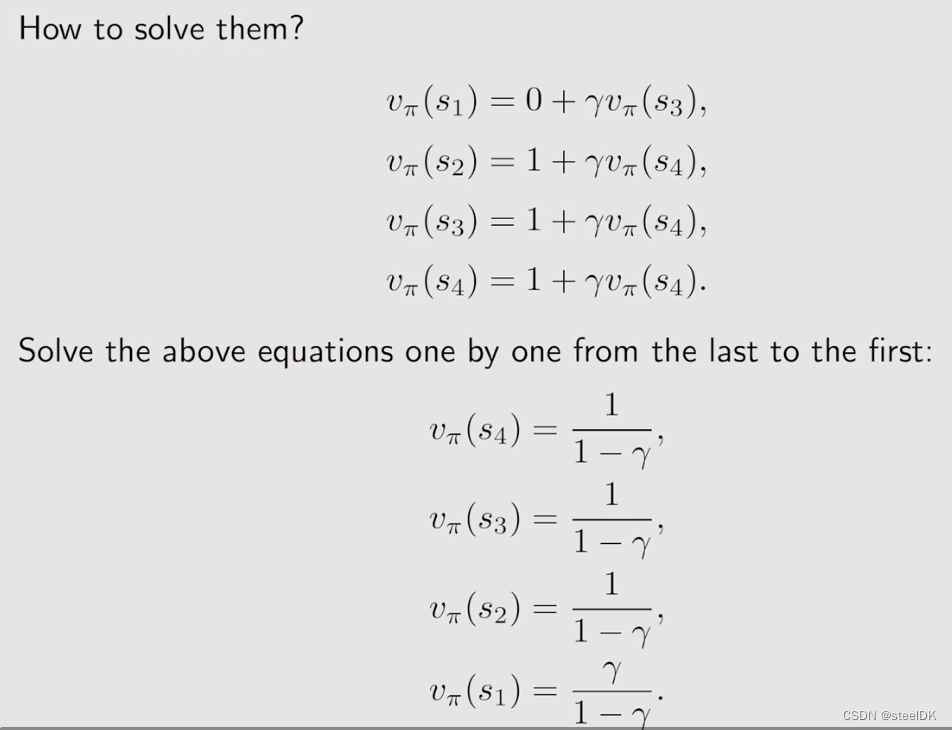

如果假设γ=0.9,得到的结果见上图。state value实际上是代表了他的价值,如果一个状态价值高,说明了这个状态是值得我们往那个方向走的,在上图中,为什么s2,s3,s4的价值高呢,是因为他们离target area是比较近的,而s1离得较远。计算得到这个状态值之后,我们就可以去改进这个策略,慢慢的我们就可以得到最优的策略。
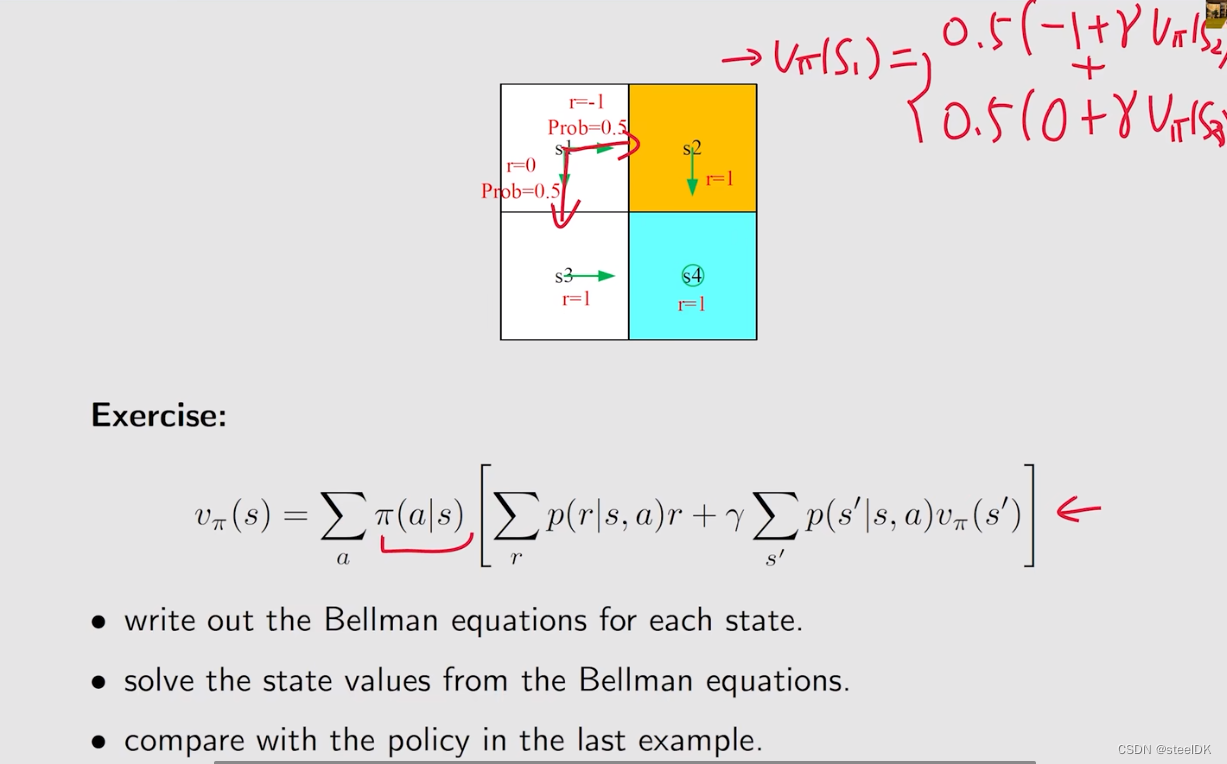

4、Bellman equation:Matrix-vector form
在上节中,我们介绍了贝尔曼公式的推导,这节来介绍贝尔曼公式的矩阵和向量形式。

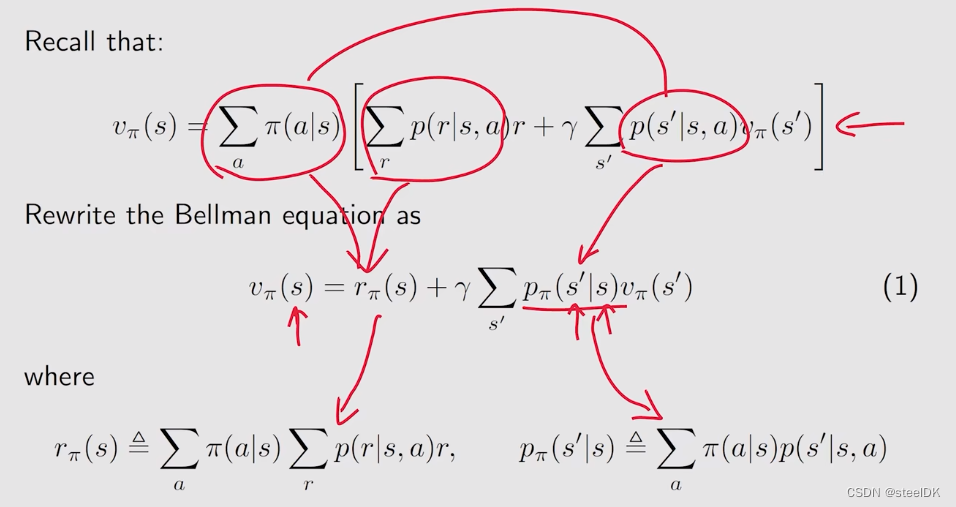
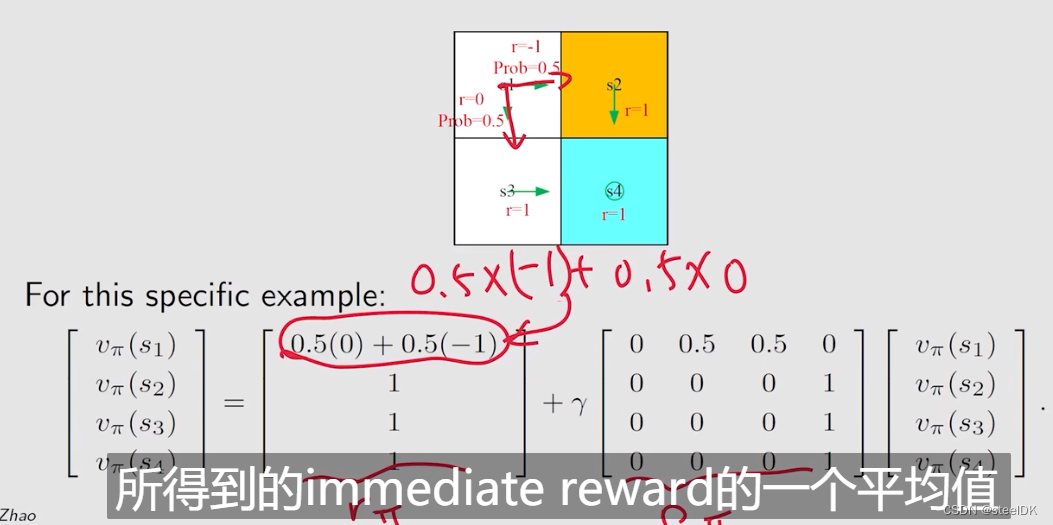
rπ(s)是从当前状态出发,得到了所有immediate reward的平均值。上式红色画的意思是展开相乘。

上图中,[Pπ]ij代表第i行第j列的元素是从si跳到sj的概率,[Pπ]ij这个矩阵也被称为状态转移矩阵。
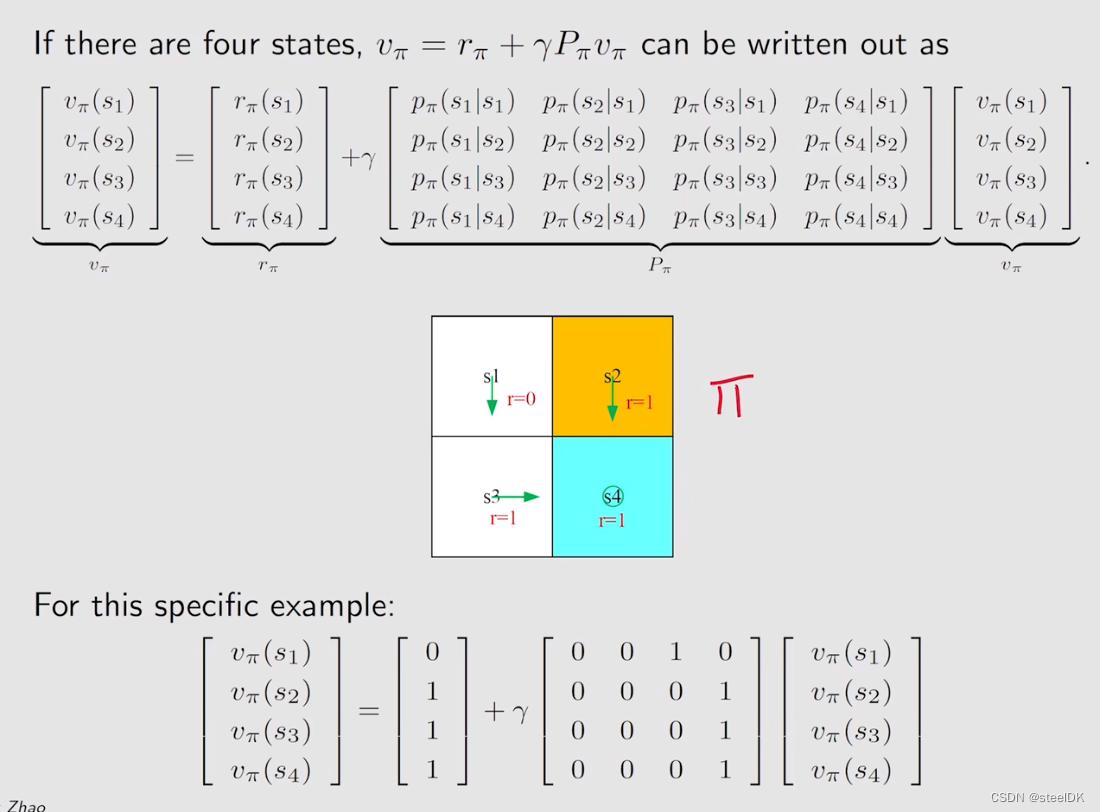
上图是当n=4时,我所得到的matrix-vector 形式,上图中的Pπ就是状态转移矩阵。在举一个例子,见下图:
4、Bellman equation:Solve the state value

首先我们来回答一下为什么要求解state value,实际上给定一个policy,然后我会列出来它的一个贝尔曼公式,再进一步求解贝尔曼公式得到state value,这样的一个过程实际上叫做policy evaluation。policy evaluation是强化学习中非常关键的一个问题,因为我们只有去评价一个策略到底好还是不好,我们才能进一步的去改进它,最后在找到最优的策略,所以求解贝尔曼公式进而得到state value是非常重要的一个问题。

求state value我们给出两种解决方案,第一种就是用求逆矩阵的方法直接求解,但是这种方法通常不会使用,因为当状态空间特别大的时候,矩阵的维度也会特别大,求逆的计算量也会特别大,所以实际当中我们使用的是迭代的方法。iterative solution方法就是从一开始随机猜一个vπ,记为v0,把这个v0带入到上图红色箭头所指的式子中,因为rπ和Pπ都是可以事先知道的,所以可以计算得到v1,然后再把v1带到右边,就又可以得到v2,依次类推,就会得到序列{v0,v1,v2,…vk},实际上我们可以证明当k趋近于无穷的时候,vk就收敛到了vπ,这个vπ就是真实的state value。为什么vk会收敛到vπ呢?下面是证明。

证明的思路是定义vk与vπ之间的误差,证明这个误差趋近于0即可。下面我们通过例子来进一步说明。

上图是两个比较好的policy,可以看到得到的状态值均为正,并且我们还可以看出,不同的策略可以得到相同的value值。下面我们在看两个不好的policy。

通过以上例子可以得出,我们可以计算state value来评价一个策略究竟是好还是坏。
5、Action value
在前几节,我们介绍了state value,以及描述state value的贝尔曼公式,下面我们将从state value转向action value。

state value和action value有什么区别与联系呢?state value指的是agent从一个状态出发,所得到的average return。action value指的是agent从一个状态出发并且选择一个action之后得到的average return。
为什么要关注action value:实际上我们一直讨论的是强化学习中的策略,策略指的是在一个状态我要选择什么样的action,action有很多,具体选择哪一个action就是通过action value来判断,action value大的意味着采取该action能够得到更多的reward。

由上图可知,state value可以和action value建立联系。有很多个action,在当前状态下,采取其中一个action的概率为π(a|s),乘以采取该动作后得到的average return。与π(a|s)相乘的那一项就是action value。


下面通过一个例子来理解action value:
上图中策略已经通过绿色箭头画出来了。
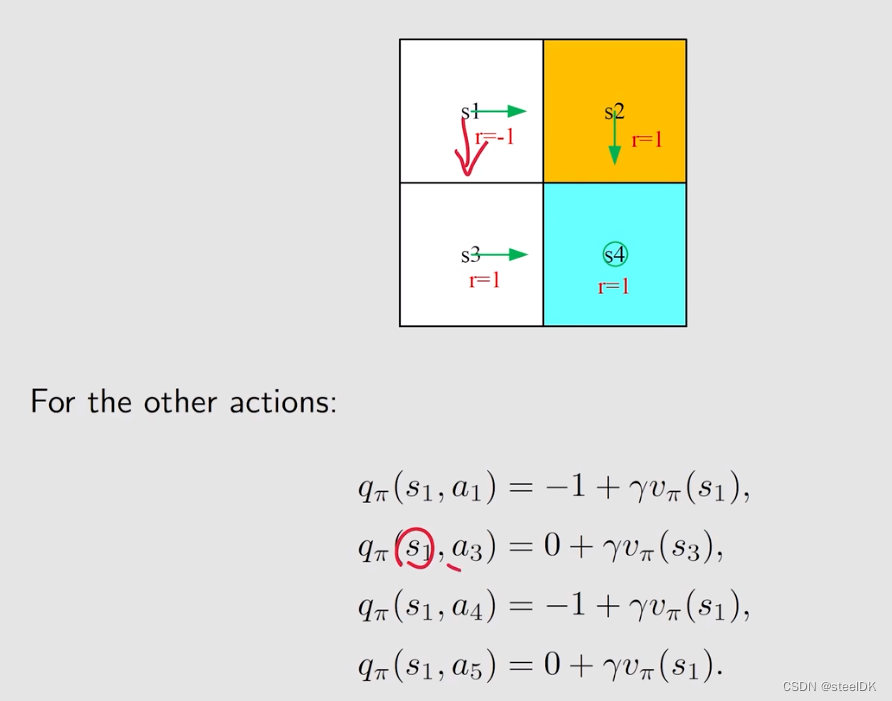
下面做一个总结:

state value满足贝尔曼公式,贝尔曼公式刻画了state value之间的公式,是求解state value的一个工具,上图是它的elementwise form,就是对每一个状态都存在这样一个式子。
相关文章:

03 贝尔曼公式
贝尔曼公式 前言1、Motivating examples2、state value3、Bellman equation:Derivation4、Bellman equation:Matrix-vector form4、Bellman equation:Solve the state value5、Action value 前言 本文来自西湖大学赵世钰老师的B站视频。本节课主要介绍贝尔曼公式。 本节课概要…...

学习视频剪辑:批量添加srt字幕,让视频更生动
随着社交媒体的普及,视频制作变得越来越重要。无论是记录生活,还是分享知识,视频都是一个非常有力的工具。但是,如何让您的视频更生动、更吸引人呢?通过学习视频剪辑,您可以使您的视频更具有吸引力。而在这…...
Windows桌面便签工具推荐使用哪一款?
电脑桌面上张贴便利贴可以将近期需要完成的工作计划逐一添加到便利贴中,电脑桌面悬挂便利贴工具可以督促日常各项事务的完成。当前可悬挂在电脑桌面上的便利贴工具是比较多的,其中桌面小工具便签软件敬业签可满足各行业的办公需求。 建议大家在Windows桌…...
)
【微信小程序】自定义组件(二)
自定义组件 纯数据字段1、什么是纯数据字段2、使用规则 组件的生命周期1、组件全部的生命周期函数2、组件主要的生命周期函数3、lifetimes节点 组件所在页面的生命周期1、什么是组件所在页面的生命周期2、 pageLifetimes节点3、生成随机的颜色值 纯数据字段 1、什么是纯数据字…...

llinux的更目录下的文件作用和举例
Linux是一种开源的操作系统,其文件系统采用了一种层次化的结构。在Linux文件系统中,最顶层的目录被称为根目录,也就是“/”(斜杠)。在根目录下,有很多文件和目录,它们各自有着不同的作用。本文将…...

20231106_抽象类abstract
抽象类abstract 关键字 abstract运用抽象类抽象方法:修饰抽象类中的某个方法,强制子类重写该方法 归纳 关键字 abstract 对于子类必须要实现特定方法,当时父类无法明确时,可定义为抽象类及抽象方法 不合理: 动物吃东西是基础,在这里写吃的方法过于简单,信息没有实际意义; 怎…...

yolov5 obb旋转框 tensorrt部署
文章目录 1.生成engine文件2.检测图像3.代码yolov5-obb tensorRT部署代码结合王新宇和fish-kong两者的代码,可以多batch批量检测旋转框 yolov5旋转框检测: https://blog.csdn.net/qq_42754919/article/details/134145174 1.生成engine文件 首先需要将pt文件转换成wts文件,…...
http中的Content-Type类型
浏览器的Content-Type 最近在做web端下载的时候需要给前端返回一个二进制的流,需要在请求头中设置一个 writer.Header().Set("Content-Type", "application/octet-stream")那么http中的Content-Type有具体有哪些呢?他们具体的使用场…...
【C语法学习】17 - fwrite()函数
文章目录 1 函数原型2 参数3 返回值4 示例 1 函数原型 fwrite():将ptr指向的内存空间中储存的数据块写入与指定流stream相关联的二进制文件中,函数原型如下: size_t fwrite(const void *ptr, size_t size, size_t count, FILE *stream)2 参…...
)
CWE(Common Weakness Enumeration,通用缺陷枚举)
参考链接:https://cwe.mitre.org/ CWE(Common Weakness Enumeration,通用缺陷枚举)和CVE(Common Vulnerabilities & Exposures,通用漏洞和风险)都是在计算机软件安全领域中非常重要的公开数…...

华为政企视频会议产品集
产品类型产品型号产品说明 maintainProductCloudMCU基础版-ARM华为CloudMCU是为面向云化需求而推出的功能强大的企业云通信融合媒体平台。融合视频、音频和数据等多种媒体内容,接入从会议室到个人PC、手机等设备,实现统一无缝的沟通协作。maintainProduc…...

IntelliJ IDEA 2022创建Maven项目
IntelliJ IDEA 2022创建Maven项目 点击New Project 配置一下下 (1). 选择Maven Archetype (2). 输入Name就是你的项目名称 (3). 输入Location是你的项目保存目录 (4). 选择JDK (5). 选择Catalog一般默认选择Internal即可 在Archetype这里我们选择一个模板来创建Maven项目 …...

有限域的Fast Multiplication和Modular Reduction算法实现
1. 引言 关于有限域的基础知识,可参考: RISC Zero团队2022年11月视频 Intro to Finite Fields: RISC Zero Study Club 有限域几乎是密码学中所有数学的基础。 ZKP证明系统中的所有运算都是基于有限域的: 使用布尔运算的数字电路…...

第八章:security testing
文章目录 Security Testingbuffer overflow 的例子Fuzzing 测试Random Testing好处坏处Mutation-based Fuzzing好处坏处Generation-based Fuzzing好处坏处Memory DebuggerUndefined Behaviors (未定义行为)Security Testing 渗透测试(或称为pentesting)是指攻击软件以寻找安…...

Linux系统下一些配置建议整理
1. 【推荐】高并发服务器建议调小 TCP 协议的 time_wait 超时时间。 说明:操作系统默认 240 秒后,才会关闭处于 time_wait 状态的连接,在高并发访问下,服 务器端会因为处于 time_wait 的连接数太多,可能无法建立新的…...

【launch文件中如何启动gdb调试单个节点多个节点】
文章目录 调试多个节点在ROS中,如果需要用gdb调试节点,你可以在.launch文件中添加相关的参数。以下是一个例子,展示如何为一个节点启动gdb调试: <launch><node pkg="your_package" type="your_node...
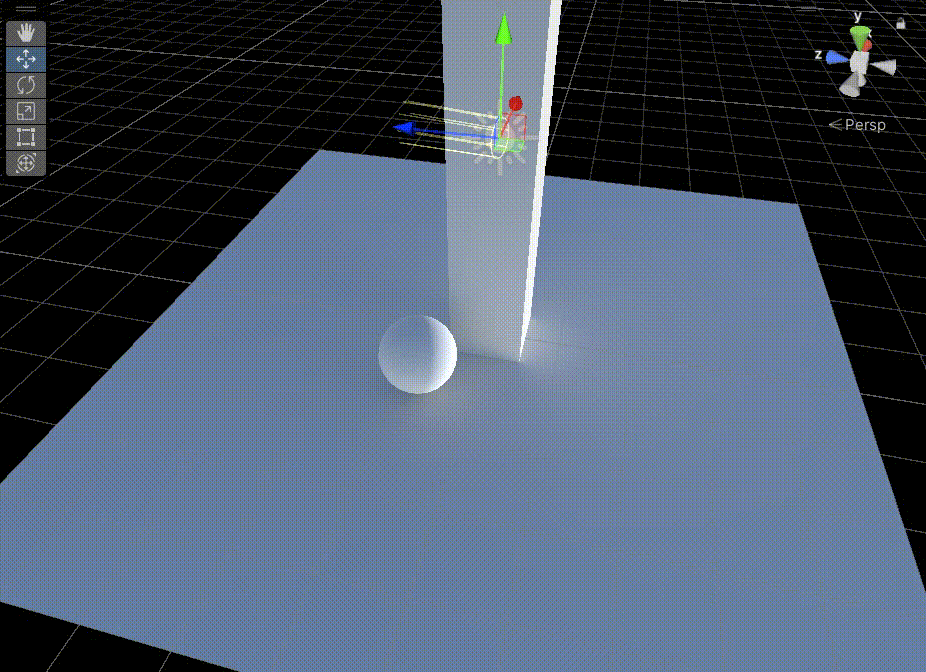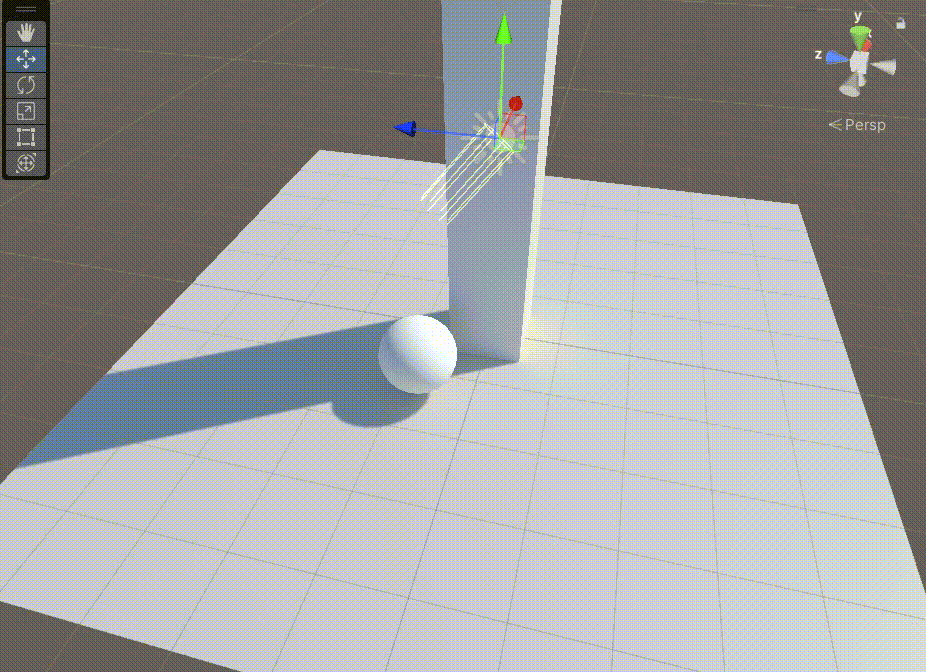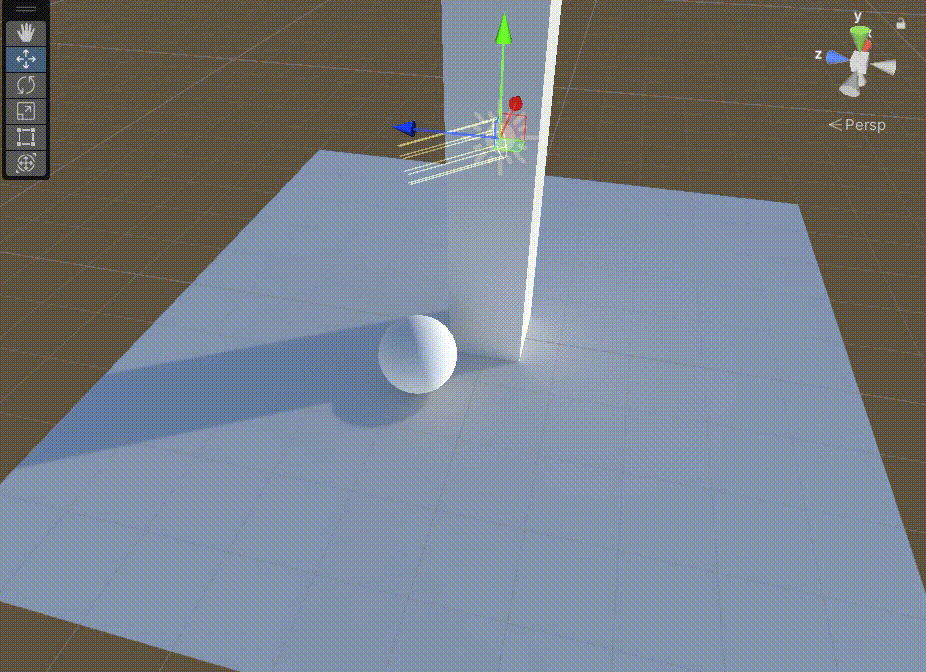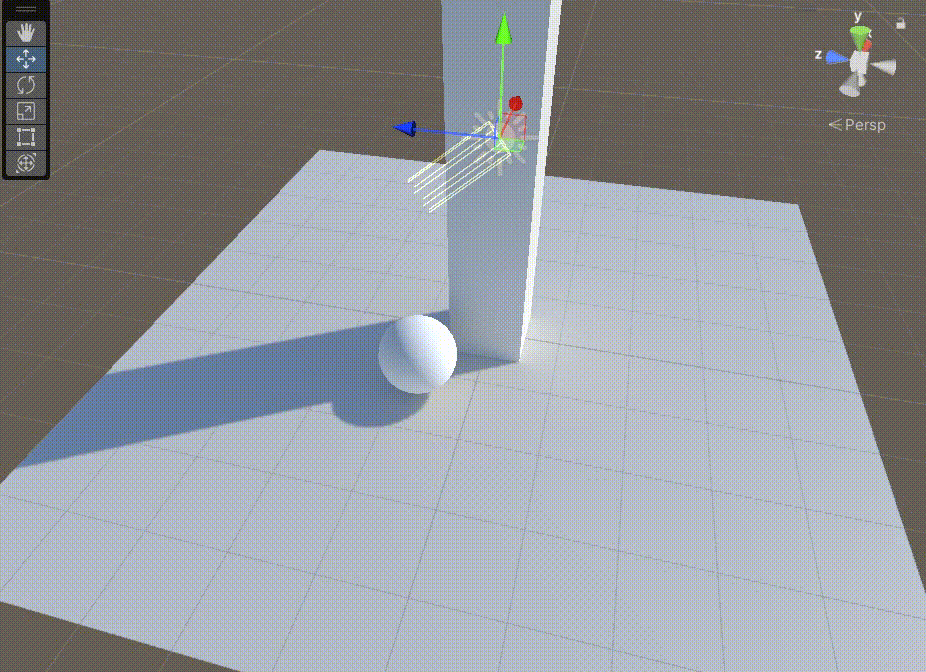
Unity中Shader的GI的直接光实现
文章目录 前言一、在上一篇文章中,得到GI相关数据后,需要对其进行Lambert光照模型计算二、在准备好上面步骤后,我们需要准备缺少的数据1、准备上图中的 s.Normal2、准备上图中的 s.Albedo 前言 Unity中Shader的GI的直接光实现,基…...

JAVA进程和线程
哈喽~大家好呀,这篇来看看JAVA进程和线程。 🥇个人主页:个人主页 🥈 系列专栏:【日常学习上的分享】 🥉与这篇相关的文章: Redis快速入…...

JS自定义深浅度克隆
function deepClone(obj, cache new WeakMap()) {if (typeof obj ! object) return obj //普通类型,直接返回if (obj null) return objif (cache.get(obj)) return cache.get(obj)//防止循环引用,程序进入死循环if (obj instanceof Date) return new D…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...