有限域的Fast Multiplication和Modular Reduction算法实现
1. 引言
关于有限域的基础知识,可参考:
- RISC Zero团队2022年11月视频 Intro to Finite Fields: RISC Zero Study Club

有限域几乎是密码学中所有数学的基础。
ZKP证明系统中的所有运算都是基于有限域的:
- 使用布尔运算的数字电路:如AND、OR、NOT。
- 使用有限域运算的算术电路:如addition、multiplication、negation。
但是,真实的计算机没有有限域电路装置,只有:
- ADD rax, rbx
- MUL rax
- SHR rax, CL
- 等等
因此,需基于以上运算来构建有限域运算。
有限域运算的速度很关键,原因在于:
- 影响ZKP可用性的最大障碍在于证明开销。
- 几乎所有的证明时间都用于有限域运算了。为提升ZKP证明速度:
- 减少有限域运算次数(如,更高效的NTT或MSM算法)
- 让有限域运算更高效(如,使用优化的有限域表示)
本文主要关注内容有:
- BigInts
- BigInts经典加法运算
- BigInts经典乘法运算
- Modular reduction(Barrett算法):当无法更改数字表示时,最有用。
- Montgomery form
- Multiplication and reduction(Montgomery算法):最常用算法。
- 其它multiplication算法
并对大整数乘法运算的经典算法、Barrett算法、Montgomery算法进行了对比:

2. 大整数及其加法和乘法运算
大整数,又名BigInt或Multiprecision Integers。
真实计算机的运算符是基于word的:
- 几乎所有的现代计算机都使用64-bit words
- 但32-bit words并未完全过时。比如在IoT世界。
对于更大(如256位)的域,会将其切分为words来表示:
- 如,通常以4个64-bit word来表示256-bit数字。
- 如十进制的8位数字,可 以4个2-digit word来表示。
如以100进制的digit来表示大整数27311837,对应为:
( 27 31 18 37 ) 100 (27\ 31\ 18\ 37)_{100} (27 31 18 37)100。
2.1 大整数经典加法运算
对应的大整数加法运算,如 ( 27 31 18 37 ) 100 + ( 88 68 97 89 ) 100 (27\ 31\ 18\ 37)_{100} + (88\ 68\ 97\ 89)_{100} (27 31 18 37)100+(88 68 97 89)100,计算规则为:

具体见Handbook of Elliptic and Hyperelliptic Curve Cryptography书本中的Algorithm 10.3算法:






2.2 大整数经典乘法运算
以 ( 54 12 ) 100 ∗ ( 36 29 ) 100 (54\ 12)_{100}*(36\ 29)_{100} (54 12)100∗(36 29)100大整数乘法运算为例,具体见Handbook of Elliptic and Hyperelliptic Curve Cryptography书本中的Algorithm 10.8算法:

对应各个step的计算数据为:

3. Modular Reduction
需注意,以上加法和乘法运算结果均为更大的值,需将这些大的结果值reduce为相应的canonical表示,如:

常见的Modular Reduction算法有:
- 1)Barret reduction算法:当无法更改数字表示时,最有用。
- 2)Montgomery multiplication and reduction算法:最常用算法。
相关博客有:
- 基础算法优化——Fast Modular Multiplication
- GPU/CPU友好的模乘算法:Multi-Precision Fast Modular Multiplication
- Montgomery reduction——多精度模乘法运算算法
3.1 Barret reduction算法
做reduction最明显的方式是做除法,但除法运算昂贵,且可能不是constant time的。以single-word除法运算 b = 1 , R = 2 k b=1,R=2^k b=1,R=2k 为例:
func reduce(a uint) uint {q:= a / n // Division implicitly returns the floor of the result.return a - q * n
}
非constant time会存在timing attack攻击问题。
Barrett reduction为将 1 / n 1/n 1/n近似为 m / 2 k m/2^k m/2k,因为 m / 2 k m/2^k m/2k中的除法实际是右移运算,要便宜得多。【可近似计算 m m m值为 m = ⌊ 2 k / n ⌋ m=\left \lfloor 2^k/n\right \rfloor m=⌊2k/n⌋】
func reduce(a uint) uint {q := (a * m) >> k // ">> k" denotes bitshift by k.return a - q * n
}
不过这样reduce之后的结果在 [ 0 , 2 n ) [0,2n) [0,2n),而不是 [ 0 , n ) [0,n) [0,n),因此需进一步reduce:
func reduce(a uint) uint {q := (a * m) >> ka -= q * nif a >= n {a -= n}return a
}
Handbook of Elliptic and Hyperelliptic Curve Cryptography书本中的Algorithm 10.17算法,将其扩展为了multi-word Barrett Reduction算法,且在以上最后一步reduce之前的结果不再是 [ 0 , 2 n ) [0,2n) [0,2n)而是可能更大的范围值,因此在Algorithm 10.17算法中第4步采用的是while:










3.2 Montgomery multiplication and reduction算法
Montgomery Form为另一种有限域表示,其支持快速combined multiplication and reduction算法。
之前将有限域元素表示为:
x ∈ [ 0 , N − 1 ] x\in [0,N-1] x∈[0,N−1]
而Montgomery Form表示定义为:
[ x ] = ( x R ) m o d N [x]=(xR)\mod N [x]=(xR)modN
Montgomery Reduction算法计算的是:
R E D C ( u ) = ( u R − 1 ) m o d N REDC(u)=(uR^{-1})\mod N REDC(u)=(uR−1)modN
而不是之前Barrett Reduction计算的 u m o d N u\mod N umodN。
R E D C REDC REDC是一个非常多功能的公式:
- 1)将经典转换为Montgomery: [ x ] = R E D C ( ( x R 2 ) m o d N ) [x]=REDC((xR^2)\mod N) [x]=REDC((xR2)modN)
- 2)将Montgomery转换为经典: R E D C ( [ x ] ) = x REDC([x])=x REDC([x])=x
- 3)对Montgomery Form表示的乘法运算: ( ( x R m o d p ) ∗ ( y R m o d p ) ∗ R − 1 m o d p ) = ( x y R ) m o d p ((xR\mod p)*(yR\mod p)*R^{-1}\mod p)=(xyR)\mod p ((xRmodp)∗(yRmodp)∗R−1modp)=(xyR)modp,对应在Handbook of Elliptic and Hyperelliptic Curve Cryptography书本中的Algorithm 11.3算法中做了相应实现:

其中 Handbook of Elliptic and Hyperelliptic Curve Cryptography书本中的Algorithm 10.22算法中所实现的Montgomery reduction算法为:










4. 其它multiplication算法
Multiplication算法的演变过程为:
- multiplication算法曾被认为其runtime约为 O ( n 2 ) O(n^2) O(n2)。
- Karatsuba发明了一种divide-and-conquer算法,其runtime为 O ( n 1.58 ) O(n^{1.58}) O(n1.58)。
- Toom-Cook乘法算法与Karatsuba算法类似,性能略好一点。
- Schönhage–Strassen 发明了一种NTT算法,其runtime为 O ( n ⋅ log n ⋅ log log n ) O(n\cdot \log n\cdot \log\log n) O(n⋅logn⋅loglogn)。
- 当对大整数做乘法运算时,其速度要更慢,如4096位RSA密钥。
参考资料
[1] RISC Zero团队2023年2月视频 Finite Field Implementations: Barrett & Montgomery【slide见Finite Field Implementations】
[2] 维基百科Barrett reduction
RISC Zero系列博客
- RISC0:Towards a Unified Compilation Framework for Zero Knowledge
- Risc Zero ZKVM:zk-STARKs + RISC-V
- 2023年 ZK Hack以及ZK Summit 亮点记
- RISC Zero zkVM 白皮书
- Risc0:使用Continunations来证明任意EVM交易
- Zeth:首个Type 0 zkEVM
- RISC Zero项目简介
- RISC Zero zkVM性能指标
- Continuations:扩展RISC Zero zkVM支持(无限)大计算
- A summary on the FRI low degree test前2页导读
- Reed-Solomon Codes及其与RISC Zero zkVM的关系
- RISC Zero zkVM架构
- RISC-V与RISC Zero zkVM的关系
相关文章:

有限域的Fast Multiplication和Modular Reduction算法实现
1. 引言 关于有限域的基础知识,可参考: RISC Zero团队2022年11月视频 Intro to Finite Fields: RISC Zero Study Club 有限域几乎是密码学中所有数学的基础。 ZKP证明系统中的所有运算都是基于有限域的: 使用布尔运算的数字电路…...

第八章:security testing
文章目录 Security Testingbuffer overflow 的例子Fuzzing 测试Random Testing好处坏处Mutation-based Fuzzing好处坏处Generation-based Fuzzing好处坏处Memory DebuggerUndefined Behaviors (未定义行为)Security Testing 渗透测试(或称为pentesting)是指攻击软件以寻找安…...

Linux系统下一些配置建议整理
1. 【推荐】高并发服务器建议调小 TCP 协议的 time_wait 超时时间。 说明:操作系统默认 240 秒后,才会关闭处于 time_wait 状态的连接,在高并发访问下,服 务器端会因为处于 time_wait 的连接数太多,可能无法建立新的…...

【launch文件中如何启动gdb调试单个节点多个节点】
文章目录 调试多个节点在ROS中,如果需要用gdb调试节点,你可以在.launch文件中添加相关的参数。以下是一个例子,展示如何为一个节点启动gdb调试: <launch><node pkg="your_package" type="your_node...
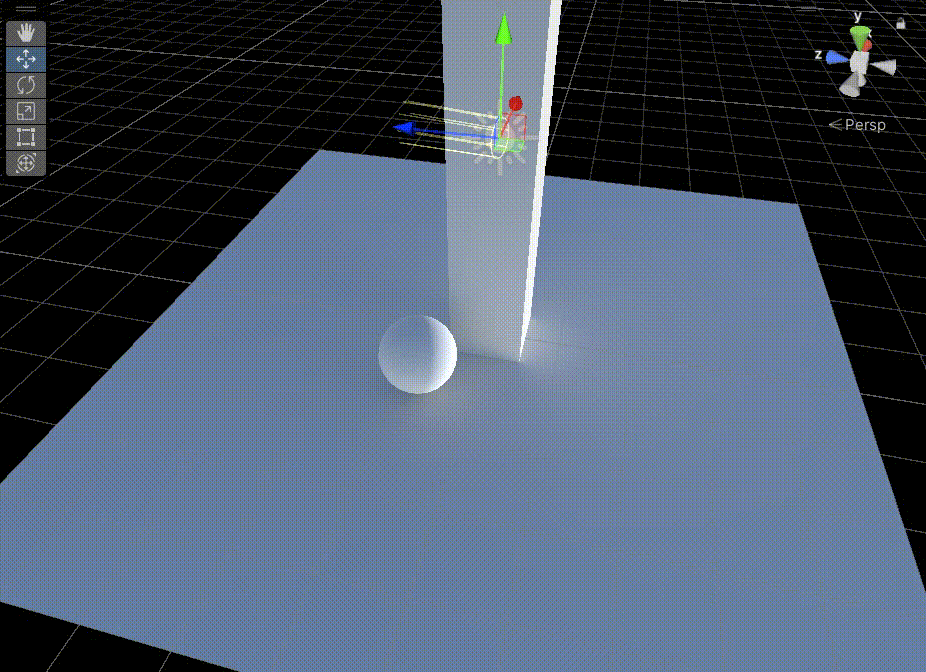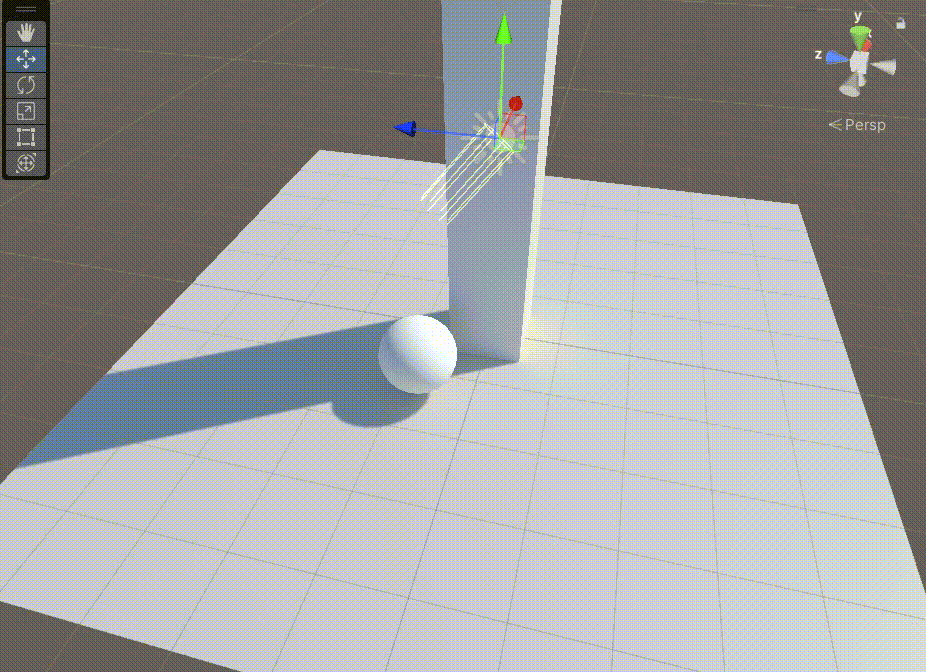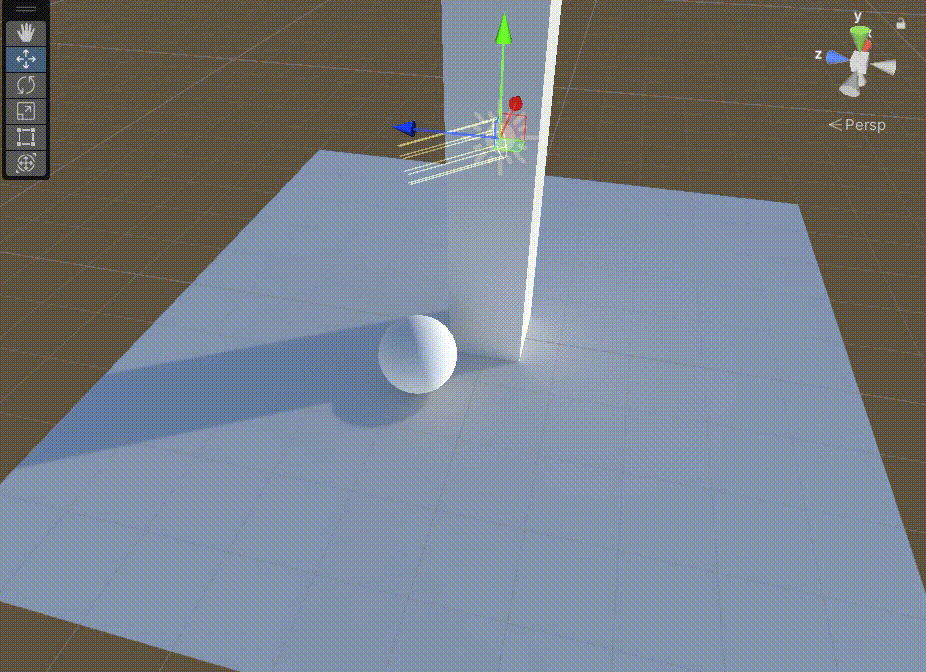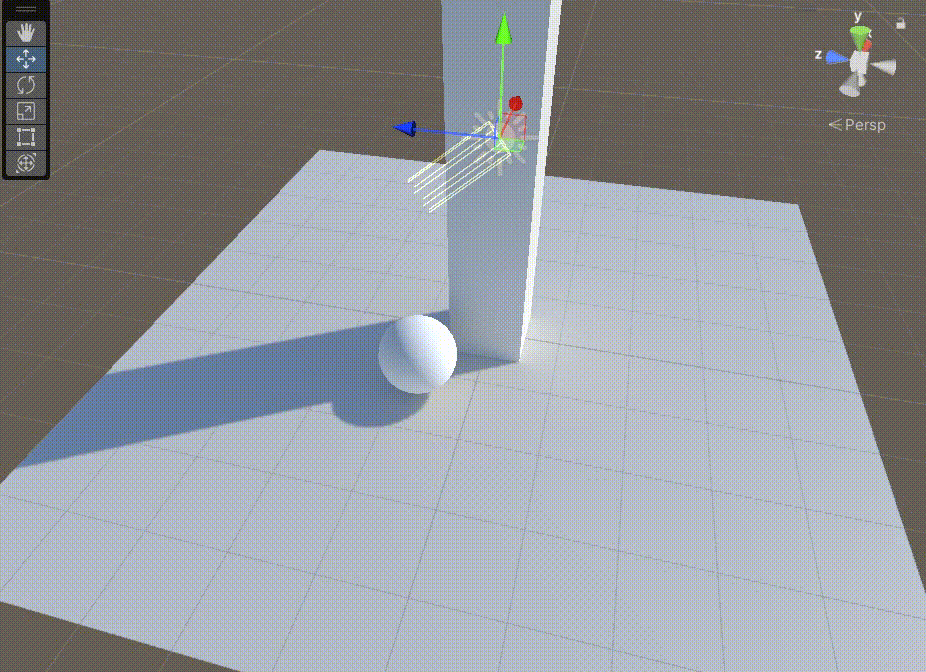
Unity中Shader的GI的直接光实现
文章目录 前言一、在上一篇文章中,得到GI相关数据后,需要对其进行Lambert光照模型计算二、在准备好上面步骤后,我们需要准备缺少的数据1、准备上图中的 s.Normal2、准备上图中的 s.Albedo 前言 Unity中Shader的GI的直接光实现,基…...

JAVA进程和线程
哈喽~大家好呀,这篇来看看JAVA进程和线程。 🥇个人主页:个人主页 🥈 系列专栏:【日常学习上的分享】 🥉与这篇相关的文章: Redis快速入…...

JS自定义深浅度克隆
function deepClone(obj, cache new WeakMap()) {if (typeof obj ! object) return obj //普通类型,直接返回if (obj null) return objif (cache.get(obj)) return cache.get(obj)//防止循环引用,程序进入死循环if (obj instanceof Date) return new D…...

MySQL之表的约束
目录 表的约束1.空属性2.默认值3.列描述4.zerofill5.主键6.自增长7.唯一键8.外键 表的约束 真正约束字段的是数据类型,数据类型规定了数据的用法、范围…假如我们没有按照其规定的约束,那么数据将插入不成功但是数据类型约束很单一,需要有一…...

Go基础——接口、并发
1、接口 Go 语言提供了另外一种数据类型即接口,它把所有的具有共性的方法定义在一起,任何其他类型只要实现了这些方法就是实现了这个接口。接口可以让不同的类型绑定到一组公共的方法上,从而实现多态和灵活的设计。Go 语言中的接口是隐式实现…...
zookeeper本地部署和集群搭建
zookeeper(动物园管理员)是一个广泛应用于分布式服务提供协调服务Apache的开源框架 Zookeeper从设计模式角度来理解:是一个基于观察者模式设计的分布式服务管理框架,它 负责存储和管理大家都关心的数据 ,然 后 接受观察…...
工程师)
优橙内推甘肃专场——5G网络优化(中高级)工程师
内推公司1:上海井胜通讯技术有限公司 内推公司2:西安长河通讯有限责任公司 内推公司3:沈阳电信工程局 上海井胜通讯技术有限公司 公司成立于2002年,是一家专业移动通信技术服务公司。2008年之前是香港一家大型流动通讯运营公司…...
crontab 定时任务
1.查看 crond 是否开启 systemctl status crond 2.设置 crontab 定时任务 基本语法 #基本语法 crontab [选项] 查看定时任务 #查看定时任务 crontab -l 编辑定时任务 #编辑定时任务 crontab -e 案例实操 */1 * * * * echo "hello,world" >> /root/hel…...
【入门Flink】- 03Flink部署
集群角色 Flik提交作业和执行任务,需要几个关键组件: 客户端(Client):代码由客户端获取并做转换,之后提交给JobManger JobManager:就是Fink集群里的“管事人”,对作业进行中央调度管理;而它获…...

DockerFile常用保留字指令及知识点合集
目录 DockerFile加深理解: DockerFile常用保留字指令 保留字: RUN:容器构建时需要运行的命令 COPY:类似ADD,拷贝文件和目录到镜像中。 将从构建上下文目录中 <源路径> 的文件/目录复制到新的一层的镜像内的 …...

怎么批量删除文件名中的空格?
怎么批量删除文件名中的空格?当我们整理文件的时候发现文件名里面有一些空格,如果空格较多,可能会造成文件名特别的长,我们一般会随手对文件进行重命名,然后将文件名中的空格删除掉,这项操作非常的简单方便…...

回顾十大数据恢复软件,帮助用于恢复丢失的文件!
您是否因丢失计算机上的重要文件而感到恐慌?你不是一个人!数据丢失是许多人面临的严重问题,但幸运的是,有许多解决方案可以恢复数据。 在本文中,我将回顾十大数据恢复软件,以帮助您恢复丢失的文件…...

【Linux】多路IO复用技术②——poll详解如何使用poll模型实现简易的一对多服务器(附图解与代码实现)
在阅读本篇博客之前,建议大家先去看一下我之前写的这篇博客,否则你很可能会一头雾水 【Linux】多路IO复用技术①——select详解&如何使用select模型在本地主机实现简易的一对多服务器(附图解与代码实现)http://t.csdnimg.cn/…...

CSS 滚动捕获 Scroll Snap
CSS 滚动捕获 Scroll Snap CSS 滚动捕获允许开发者通过声明一些位置(或叫作捕获位置)来创建精准控制的滚动体验. 通常来说轮播图就是这种体验的例子, 在轮播图中, 用户只能停在图 A 或者图 B, 而不能停在 A 和 B 的中间. 比如平时用淘宝或小红书, 当你上滑到下一个推荐内容时…...

【带头学C++】----- 三、指针章 ---- 3.9 数组作为函数的参数
当数组作为函数参数时,有几种常见的方式可以传递数组给函数: 数组作为指针传递: 数组名在函数调用时会自动转换为指向数组第一个元素的指针。通过指针可以访问数组元素,但无法获取数组的大小。在函数中修改指针指向的值会影响原始…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...