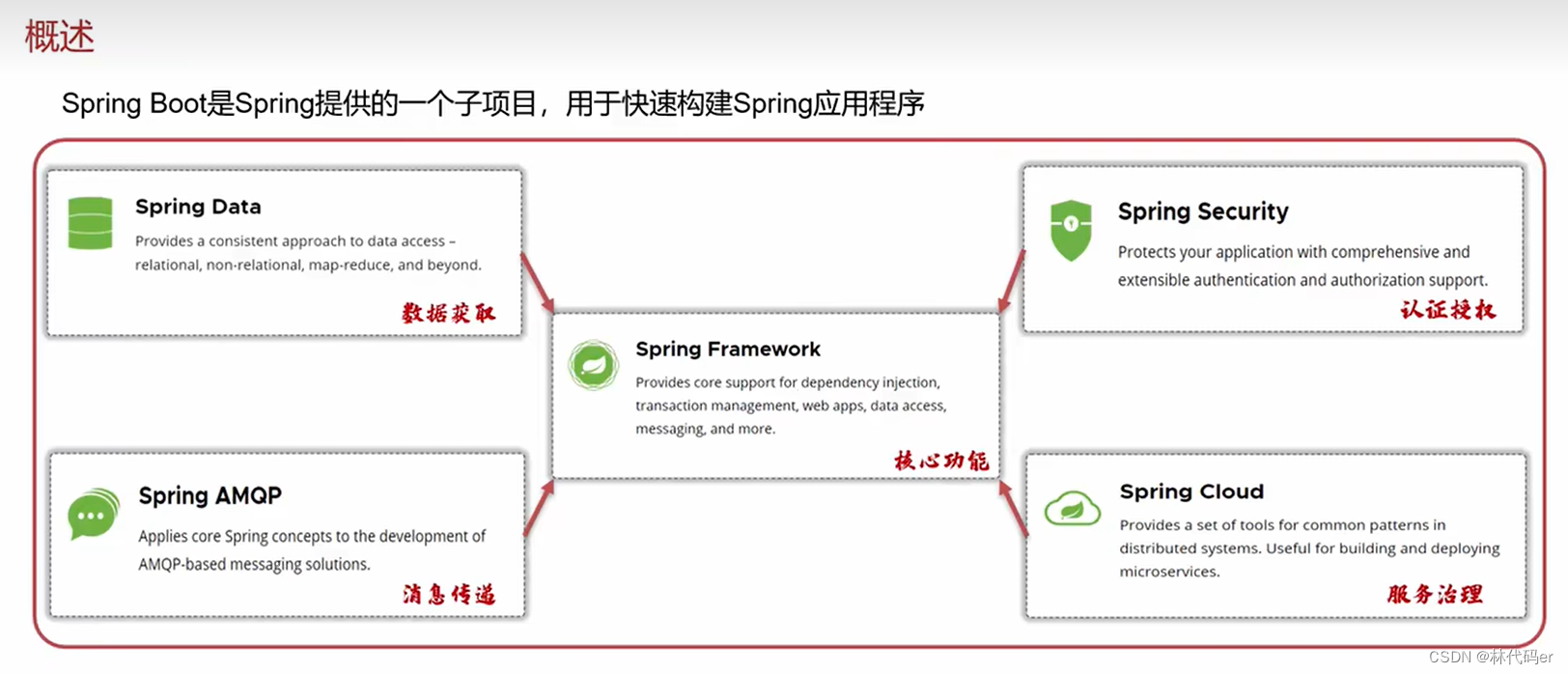
SpringBoot概述
SpringBoot是Spring提供的一个子项目,用于快速构建Spring应用程序。
- SpringFramework:核心功能
- SpringData:数据获取
- SpringSecurity:认证授权
- SpringAMQP:消息传递
- SpringCloud:服务治理
SpringBoot新特性:
1、起步依赖:
本质上就是一个Maven坐标,整合了完成一个功能需要的所有坐标。


2、自动配置:
遵循约定大于配置的原则,在boot程序启动后,一些bean对象会自动注入到ioc容器中,不需要手动声明,简化开发。
传统spring开发:引入mybatis依赖,声明bean对象
Springboot自动装配:引入mybatis起步依赖即可。

3、其他特性
- 内嵌tomcat、jetty(无需部署war文件)
- 外部化配置(修改完配置直接重启,无需再编译)
- 不需要XML配置(properties/yml)
相关文章:

SpringBoot概述
SpringBoot是Spring提供的一个子项目,用于快速构建Spring应用程序。 SpringFramework:核心功能SpringData:数据获取SpringSecurity:认证授权SpringAMQP:消息传递SpringCloud:服务治理 SpringBoot新特性&…...
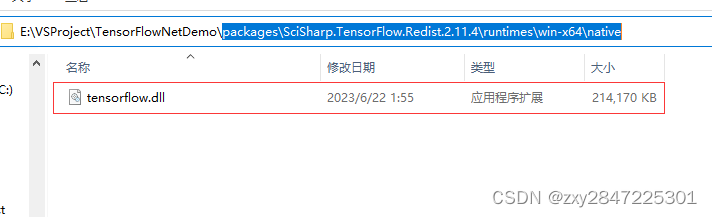
深度学习框架TensorFlow.NET环境搭建1(C#)
测试环境 visual studio 2017 window10 64位 测试步骤如下: 1 新建.net framework控制台项目,工程名称为TensorFlowNetDemo,.net framework的版本选4.7.2,如下图: 2 分别安装TensorFlow.NET包(先装)和SciSharp.…...
Git客户端软件 Tower mac中文版特点说明
Tower mac是一款Mac OS X系统上的Git客户端软件,它提供了丰富的功能和工具,帮助用户更加方便地管理和使用Git版本控制系统。 Tower mac软件特点 1. 界面友好:Tower的界面友好,使用户能够轻松地掌握软件的使用方法。 2. 多种Git操…...
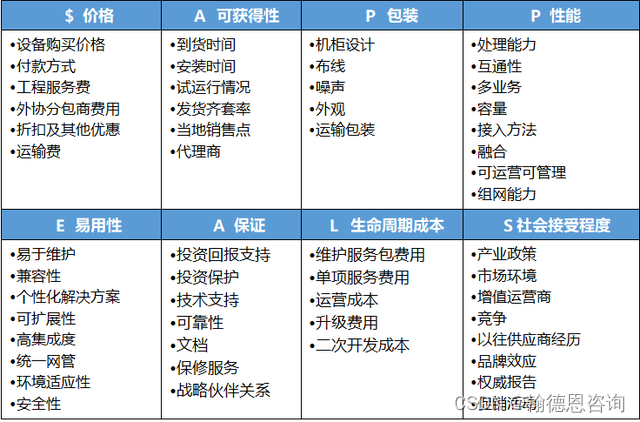
详解IPD需求分析工具$APPEALS
够让企业生存下去的是客户,所以,众多企业提出要“以客户为中心”,那如何做到以客户为中心?IPD中给出的答案是需求管理。 需求管理流程,是IPD(集成管理开发)体系中的四大支撑流程之一࿰…...

318. 最大单词长度乘积
这道题求没有重复字母的两个字符串的最大长度乘积 重点在于怎么判断两个字符串没有重复字母 题目中只有小写字母,最多26个,于是想到使用26位二进制数来代表每一个字符串 有哪个字母就在对应位置设1 这个转换使用的是num | 1 << (c-a); 对字符串中的…...
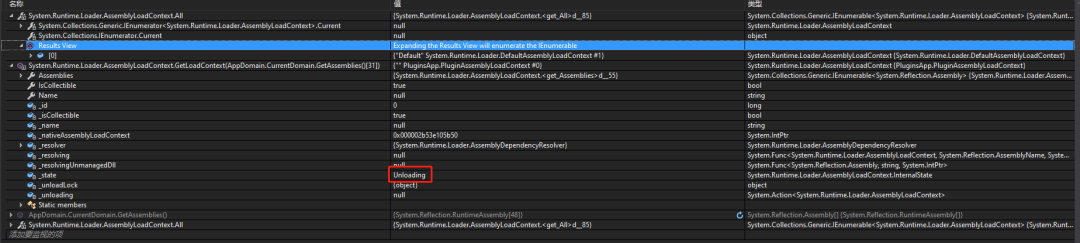
.NET Core 中插件式开发实现
在 .NET Framework 中,通过AppDomain实现动态加载和卸载程序集的效果;但是.NET Core 仅支持单个默认应用域,那么在.NET Core中如何实现【插件式】开发呢? 一、.NET Core 中 AssemblyLoadContext的使用 1、AssemblyLoadContext简…...

并查集模版以及两道例题
💯 博客内容:并查集 😀 作 者:陈大大陈 🚀 个人简介:一个正在努力学技术的准C后端工程师,专注基础和实战分享 ,欢迎私信! 💖 欢迎大家:这里是C…...
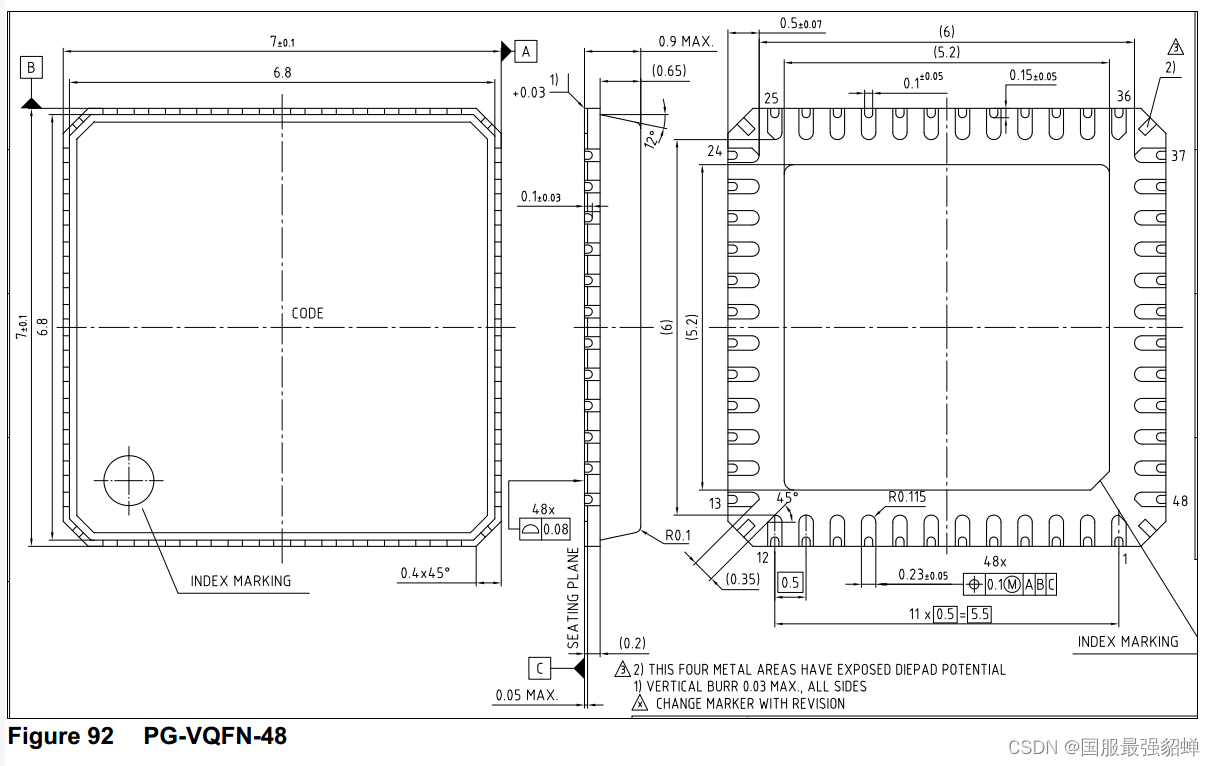
英飞凌TLF35584规格书中文
官网: 英飞凌TLF35584QVVS2 TLF35584_SPI: 1 Overview2 Block Diagram3 Pin Configuration3.1 Pin Assignment - PG-VQFN-48 4 General Product Characteristics4.1 Absolute Maximum Ratings 绝对最大额定值4.2 Functional Range4.3 Thermal Resistance…...

【教3妹学编程-算法题】最大单词长度乘积
3妹:哇,今天好冷啊, 不想上班。 2哥:今天气温比昨天低8度,3妹要空厚一点啊。 3妹 : 嗯, 赶紧把我的羽绒服找出来穿上! 2哥:哈哈,那倒还不至于, 不过气温骤降&…...
遇到python程序是通过sh文件启动的,如何调试
说明 下载的源码总会遇到这样启动的: 并且发现shell文件内容很多,比较复杂,比如: 解决方案 这时候想要调试,可以通过端口连接的方式调试,具体方法如下: 在vscode调试按钮中添加远程附加调试…...

应用系统集成-Spring Integration
应用系统集成-Spring Integration 图1 EIP 消息系统模式全景图。 Spring Integration 是系统集成的一个实现框架,提供了对EIP核心概念:Endpoint、Message、Channel、Router、Translator的抽象及相关框架实现,使得基于Spring Integration进行…...

亚马逊与TEMU平台欧代英代如何注册?注册欧代/英代流程及注意事项
亚马逊与TEMU平台欧代英代如何注册?注册欧代/英代流程及注意事项 亚马逊平台的商家的产品,由于受到欧盟商品安全新法规市场监管法规欧盟要求所有标有CE标志的商品,都要拥有欧盟境内的欧代作为商品合规的联系方式(也称为负责人)。由于英国脱离…...
【嵌入式开发工具】STM32+Keil实现软件工程搭建与开发调试
本篇文章介绍了使用Keil来对STM32F103C8芯片进行初始工程搭建,以及开发与工程调试的完整过程,帮助读者能够在实战中体会到Keil这个开发环境的使用方法,了解一个嵌入式工程从无到有的过程,并且具备快速搭建一个全新芯片对应最小软件…...

python 去除图像中的框
最近在做图像标注,会出现以下的图片,需要去除其中的边框。 1.思路 人工标注画框的范围P,并使用标注工具在画框上画一个点A。获取点A的坐标和颜色。在范围P内,将与点A颜色相似的每一个点x的颜色,替换为点x上下&#…...

企业邀约媒体的方式方法?-(快速精准)
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 快速而精确地邀约媒体通常需要有计划和策略性的方法。以下是一些方法,可以帮助企业有效地邀请媒体: 1. 媒体列表构建:首先,建立一个精心筛…...

旅游业为什么要选择VR全景,VR全景在景区旅游上有哪些应用
引言: VR全景技术的引入为旅游业带来了一场变革。这项先进技术不仅提供了前所未有的互动体验,还为景区旅游文化注入了新的生机。 一.VR全景技术:革新旅游体验 1.什么是VR全景技术? VR全景技术是一种虚拟现实技术&am…...
搭建第一个区块链网络与一键部署WeBASE步骤
官网 搭建第一个区块链网络 — FISCO BCOS v2 v2.9.0 文档 (fisco-bcos-documentation.readthedocs.io) 一键部署 — WeBASE v1.5.5 文档 (webasedoc.readthedocs.io) 步骤 默认如MySQL、Python、java等依赖已经引入 1.创建操作目录, 下载安装脚本 创建操作目录 cd ~ &a…...
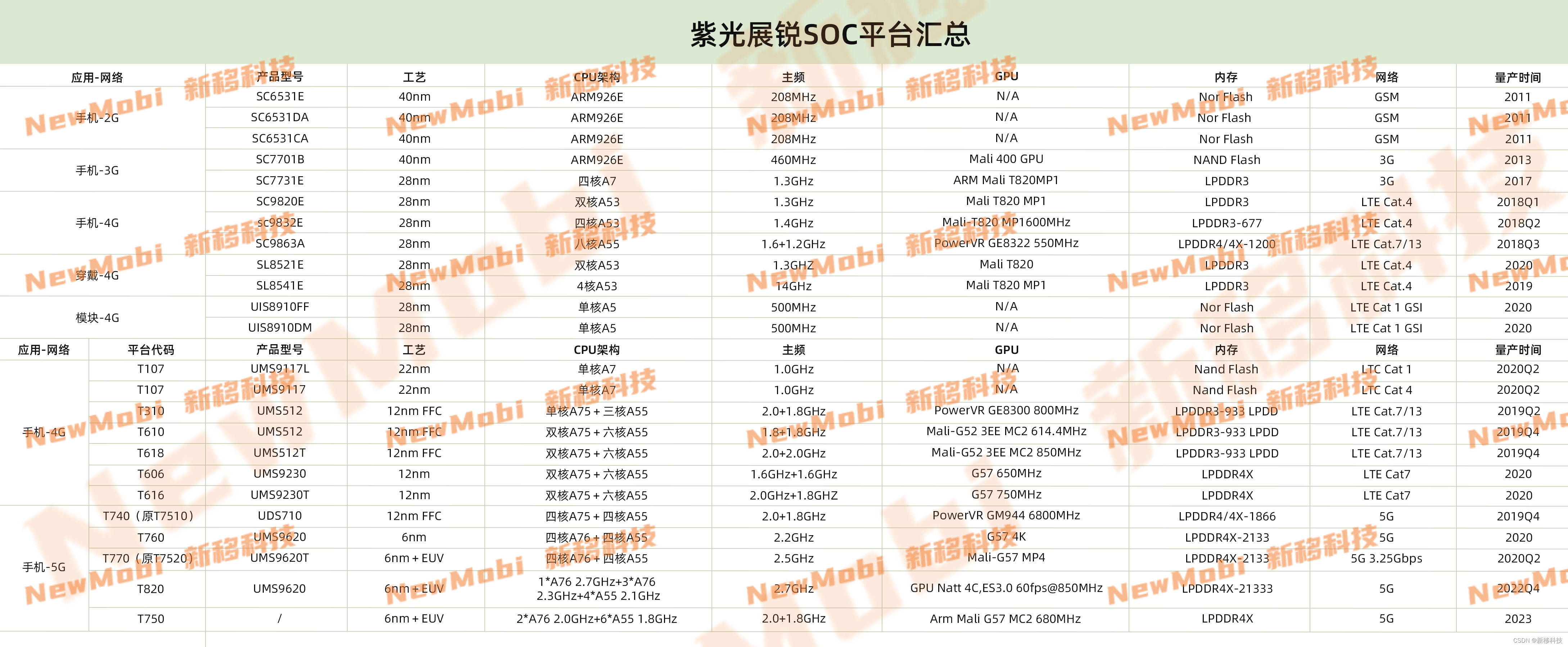
MTK联发科、高通、紫光展锐手机SOC平台型号汇总(含详细参数)
MediaTek联发科手机平台汇总: Qualcomm高通SOC平台汇总: 紫光展锐SOC平台汇总: 新移科技已成功研发手机SOC平台: 联发科平台: MTK6739、MTK6761、MTK6762、MTK6765、MTK8788、MTK6853、MTK6873、MTK6833、MTK6877、…...

【ARM AMBA AXI 入门 12 -- AXI协议中的 WLAST 与 RLAST】
文章目录 AXI协议中的 WLAST 与 RLAST AXI协议中的 WLAST 与 RLAST AMBA AXI协议是由ARM公司定义的一种高性能,高频率的总线协议。总线协议中的 WLAST 信号是一个重要的信号,它在 AXI 协议中用来标识一个突发(Burst)传输的最后一…...
)
11.6 知识总结(筛选器方法、操作标签、事件)
一、 筛选器方法 document.getElementById()------>标签对象------------>直接就是标签 $(document.getElementById()) -------> jQuery对象-------->可以使用jQuery提供的方法 jQuery(document.getElementById()) -------> jQuery对象-------->可以使用jQue…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
