数据结构初阶---复杂度的OJ例题
复杂度的OJ例题
- 一、消失的数字
- 1.思路一
- 2.思路二
- 3.思路三
- 二、旋转数组
- 1.思路一
- 2.思路二
- 3.思路三
一、消失的数字
数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(N)时间内完成吗?
链接:力扣:消失的数字
1.思路一
排序+遍历:如果下一个数据不等于上一个数据加1,那么下一个数据就是那个消失的数字。
时间复杂度:O(N*LogN)由于这个时间复杂度时间复杂度过高,本思路不再冗余,赘述。
2.思路二
利用等差数列公式:从0加到n,然后再减去这个数组中的所有数字,那么最终所得的差就是缺失的数字。
时间复杂度:O(N)
代码如下:
#include <stdio.h>
int missingNumber(int* nums, int numsSize)
{int N = numsSize;int ret = N * (N + 1) / 2;for (int i = 0; i < N; i++){ret -= nums[i];}return ret;
}int main()
{int nums[] = { 0,1,2,3,4,5,7,8,9,10 };int sz = sizeof(nums) / sizeof(nums[0]);int ret=missingNumber(nums,sz);printf("%d", ret);return 0;
}
3.思路三
单身狗思路:利用:按位异或运算符:^(相同为0,相异为1)任何数字和0 ^ 还等于它本身。首先我们要把一个完整的数组按位异或起来,然后再与题目中缺失一个数字的数组再进行按位异或,最终得到的结果就是消失的数字。
代码如下:
#include <stdio.h>
int missingNumber(int* nums, int numsSize)
{int N = numsSize;int x = 0;//第1个循环的目的:先把一个完整的数组:从0~n的所有数字全部按位异或起来存放在一个数字x中//注意:这里循环的终止条件是:<=N,(因为我们连N也要算上)for (int i = 0; i <= N; i++){x ^= i;}//第2个循环的目的:就是让一个完整的数组与缺失一个数字的数组进行按位异或,最终得到的结果就是那个消失的数字!//注意:这里循环的终止条件是:<N,(因为nums数组中确失一个数字)for (int i = 0; i < N; i++){x ^= nums[i];}return x;
}int main()
{int nums[] = { 0,1,2,3,4,5,7,8,9,10 };int sz = sizeof(nums) / sizeof(nums[0]);int ret=missingNumber(nums,sz);printf("%d", ret);return 0;
}
二、旋转数组
链接力扣:旋转数组
1.思路一
中规中矩:依次向左旋转K个数据
合计旋转:K%N次
时间复杂度:O(N^2)
空间复杂度:O(1)
因为时间复杂度超过限制,所以说不予实现。
2.思路二
核心思想:以空间换时间:我额外开辟一个数组,直接复制从k开始后面所有数据到前面,然后把复制n-k的数字放后面。
时间复杂度:O(N)
空间复杂度:O(N)
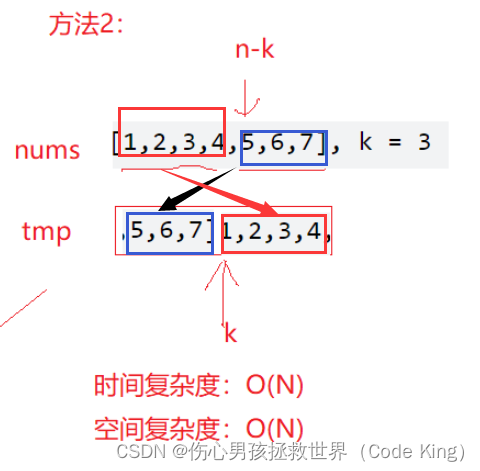
代码如下:
void rotate(int* nums, int numsSize, int k)
{int n = numsSize;int* tmp = (int*)malloc(sizeof(int) * n);k %= n;//一定别忘了k%n!memcpy(tmp, &nums[n - k], sizeof(int) * k);memcpy(&tmp[k], nums, sizeof(int) * (n - k));memcpy(nums, tmp, sizeof(int) * n);free(tmp);//一定别忘了Free!!!因为是动态开辟的空间
}int main()
{int nums[] = { 1,2,3,4,5,6,7 };int k = 0;printf("请输入你想要旋转的次数:");scanf("%d", &k);int sz = sizeof(nums) / sizeof(nums[0]);rotate(nums, sz, k);for (int i = 0; i < sz; i++){printf("%d ", nums[i]);}return 0;
}
3.思路三
数学思想:以k为划分界线,左边逆置,右边逆置,整体逆置。

代码如下:
//逆置函数
void Inversion(int* nums, int left, int right)
{while (left < right){int tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;left++;right--;}
}
//旋转函数
void rotate(int* nums, int numsSize, int k)
{int n = numsSize;k %= n;Inversion(nums, 0, n - k - 1);//左边逆置Inversion(nums, n - k, n - 1);//右边逆置Inversion(nums, 0, n - 1);//整体逆置}int main()
{int nums[] = { 1,2,3,4,5,6,7 };int k = 0;printf("请输入你想要旋转的次数:");scanf("%d", &k);int sz = sizeof(nums) / sizeof(nums[0]);rotate(nums, sz, k);for (int i = 0; i < sz; i++){printf("%d ", nums[i]);}return 0;
}
好了,今天的分享就到这里了
如果对你有帮助,记得点赞👍+关注哦!
我的主页还有其他文章,欢迎学习指点。关注我,让我们一起学习,一起成长吧!

相关文章:

数据结构初阶---复杂度的OJ例题
复杂度的OJ例题 一、消失的数字1.思路一2.思路二3.思路三 二、旋转数组1.思路一2.思路二3.思路三 一、消失的数字 数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(N)时间内完成吗? 链接:力扣&…...

Prometheus|云原生|grafana的admin用户密码重置备忘记录
很久很久以前部署的一个Prometheus套装里的grafana密码给忘记了,回忆总是很痛苦,因此还是在这里简单的记录一下,下次就不需要满世界反翻找了。 一, 改库重置密码为admin grafana密码存放在哪里的? 必须说明一下&am…...

[hive]中的字段的数据类型有哪些
Hive中提供了多种数据类型用于定义表的字段。以下是Hive中常见的数据类型: 布尔类型(Boolean):用于表示true或false。 字符串类型(String):用于表示文本字符串。 整数类型(Intege…...
第六章 树【数据结构和算法】【精致版】
第六章 树【数据结构和算法】【精致版】 前言版权第六章 树6.1 应用实例6.2 树的概念6.2.1树的定义与表示6.2.2 树的基本术语6.2.3树的抽象数据类型定义 6.3 二叉树6.3.1二叉树的定义6.3.2 二叉树的性质6.3.3 二叉树的存储 6.4 二叉树的遍历6.4.1 二叉树的遍历及递归实现**1-二…...
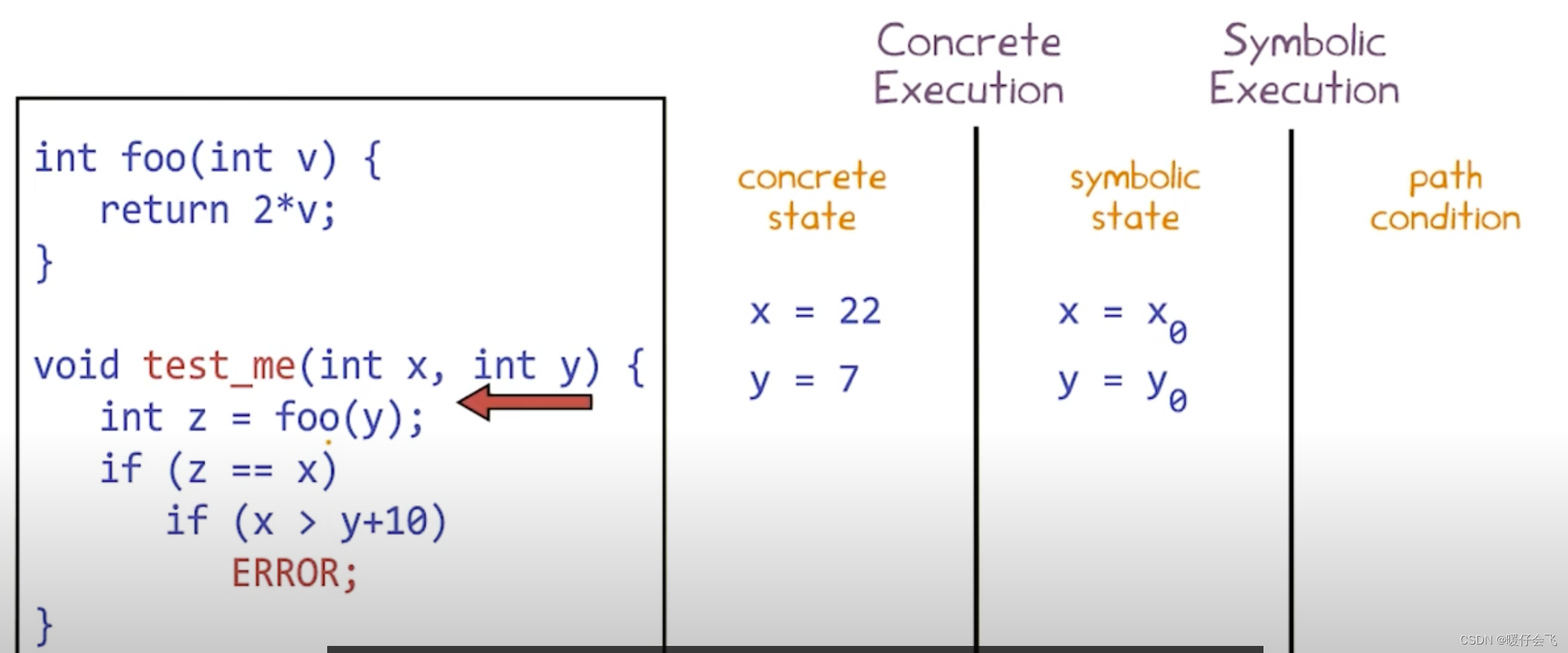
第九章:Dynamic Symbolic Execution
文章目录 Dynamic Symbolic Executionoverviewmotivationdynamic symbolic execution常用的其他技术对比Random Testingsymbolic executionCombined static and symbolic - Dynamic Execution (DSE)step1: 初始化两个具体的值 x,ystep2: 根据定义得出 z 的 concrete value 和 s…...
在搜索引擎中屏蔽csdn
csdn是一个很好的技术博客,里面信息很丰富,我也喜欢在csdn上做技术笔记。 但是CSDN体量太大,文章质量良莠不齐。当在搜索引擎搜索技术问题时,搜索结果中CSDN的内容占比太多,导致难以从其他优秀的博客平台中获取信息。因…...
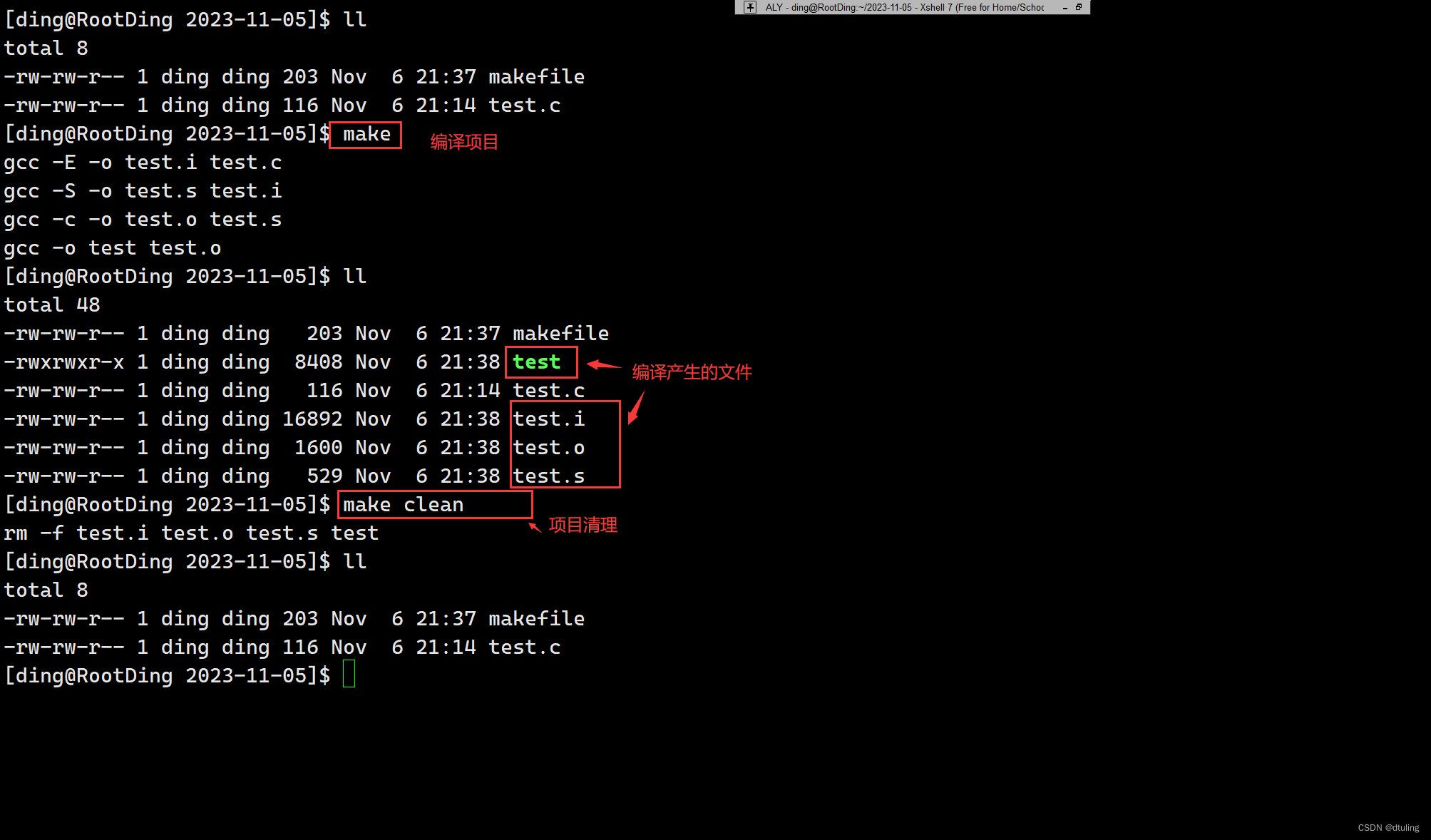
Linux开发工具的使用(vim、gcc/g++ 、make/makefile)
文章目录 一 :vim1:vim基本概念2:vim的常用三种模式3:vim三种模式的相互转换4:vim命令模式下的命令集- 移动光标-删除文字-剪切/删除-复制-替换-撤销和恢复-跳转至指定行 5:vim底行模式下的命令集 二:gcc/g1:gcc/g的作用2:gcc/g的语法3:预处理4:编译5:汇编6:链接7:函…...

MySQL(10):创建和管理表
基础知识 在 MySQL 中,一个完整的数据存储过程总共有 4 步,分别是:创建数据库、确认字段、创建数据表、插入数据。 要先创建一个数据库,而不是直接创建数据表:从系统架构的层次上看,MySQL 数据库系统从大到…...

Python赋值给另一个变量且不改变原变量
Python赋值给另一个变量且不改变原变量 在Python中,如果你想将一个变量的值赋给另一个变量,同时保持原变量不变,你可以使用复制(copy)而不是引用(reference)。Python中的变量通常是通过引用&…...
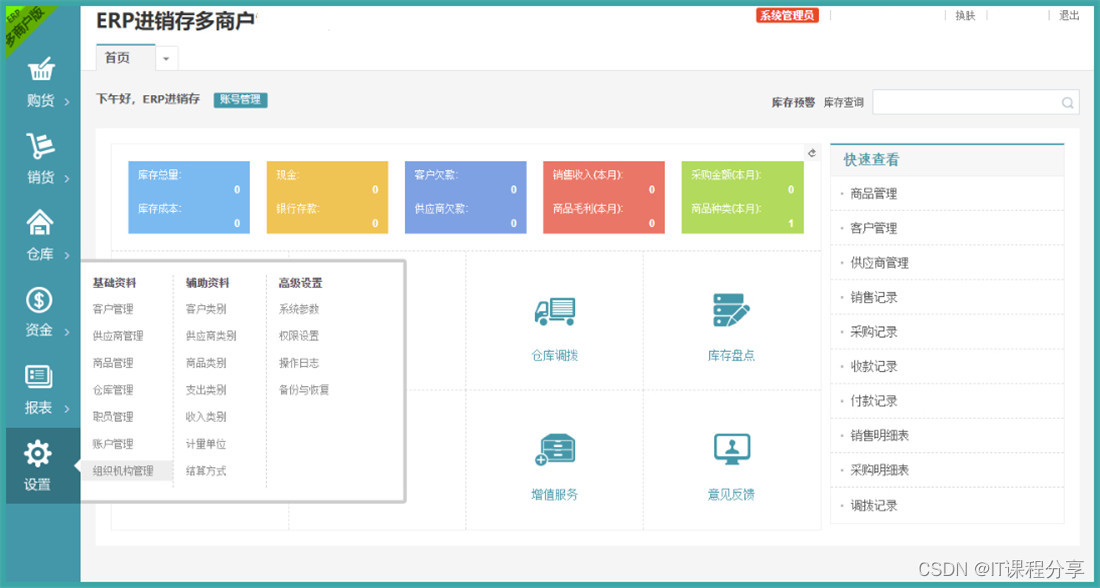
PHP进销存ERP系统源码
PHP进销存ERP系统源码 系统介绍: 扫描入库库存预警仓库管理商品管理供应商管理。 1、电脑端手机端,手机实时共享,手机端一目了然。 2、多商户Saas营销版 无限开商户,用户前端自行注册,后台管理员审核开通 3、管理…...
)
npm i 报错:Cannot read properties of null (reading ‘refs‘)
问题: 旧项目要更改东西,重新部署上线的时候,发现页面显示有异常。当时在开发环境是没有问题的。后经排查是一个引入swiper的页面报错了,只要注释掉swiper插件,就没问题了,但这肯定是不行的。 原因: npm和…...
C#学习中关于Visual Studio中ctrl+D快捷键(快速复制当前行)失效的解决办法
1、进入VisualStudio主界面点击工具——>再点击选项 2、进入选项界面后点击环境——>再点击键盘,我们可用看到右边的界面的映射方案是VisualC#2005 3、 最后点击下拉框,选择默认值,点击之后确定即可恢复ctrlD的快捷键功能 4、此时可以正…...

银河E8,吉利版Model 3:5米大车身、45寸大屏、首批8295座舱芯
作者 | Amy 编辑 | 德新 吉利银河E8在曝光后多次引爆热搜,李书福更是赞誉有加,称其为「买了就直接享受」。这款备受瞩目的车型于 10月30日晚首次亮相。 虽然新车外观在今年上海车展上早已曝光,但这次的发布会却带来了不少惊喜。新车架构以及…...

技术分享 | 被测项目需求你理解到位了么?
需求分析是开始测试工作的第一步,产品会先产出一个需求文档,然后会组织需求宣讲,在需求宣讲中分析需求中是否存在问题,然后宣讲结束后,通过需求文档分析测试点并且预估排期。所以对于需求的理解非常重要。 需求文档 …...

[MRCTF2020]你传你呢1
提示 只对php以及phtml文件之类的做了防护content-type.htaccess文件 这里就不整那么麻烦直接抓包测试 首先对后缀测试看过滤了哪些 (php php3 pht php5 phtml phps) 全部被ban了 到这里的后续思路通过上传一些配置文件把上传的图片都以php文件执行 尝试上传图片码, 直接上传成…...

一些对程序员有用的网站
当你遇到问题时 Stack Overflow:订阅他们的每周新闻和任何你感兴趣的主题Google:全球最大搜索引擎必应:在你无法使用Google的时候CSDN:聊胜于无AI导航一号AI导航二号 新闻篇 OSCHINA:中文开源技术交流社区 针对初学…...
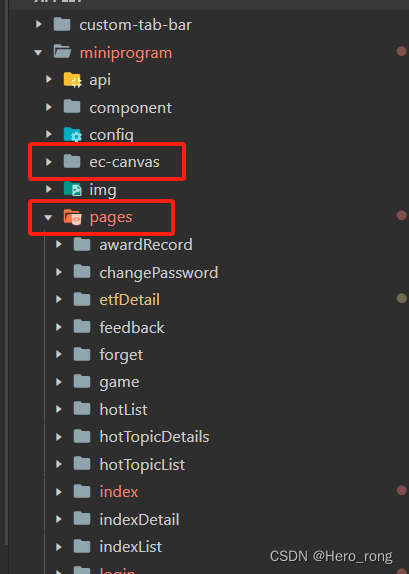
小程序使用echarts(超详细教程)
小程序使用echarts第一步就是先引用到小程序里面,可以直接从这里下载 文件很多,我们值下载 ec-canvas 就好,下载完成后,直接放在pages同级目录下 index.js 在我们需要的页面的 js 文件顶部引入 // pages/index/index.js impor…...
js控制输入框中的光标位置
主要逻辑 主要应用selectionStart、selectionEnd来实现 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title…...
Openssl生成证书-nginx使用ssl
Openssl生成证书并用nginx使用 安装openssl yum install openssl -y创库目录存放证书 mkdir /etc/nginx/cert cd /etc/nginx/cert配置本地解析 cat >>/etc/hosts << EOF 10.10.10.21 kubernetes-master.com EOF10.10.10.21 主机ip、 kubernetes-master.com 本…...

Go语言实现数据结构栈和队列
Go语言实现数据结构栈和队列 1、栈 package mainimport "fmt"func main(){// 创建栈stack : make([]int, 0)// push压入栈stack append(stack, 10)// pop弹出v : stack[len(stack)-1]// 10fmt.Println(v)stack stack[:len(stack)-1]// 检查栈空// truefmt.Printl…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
