数字化转型:云表低代码开发助力制造业腾飞
数字化转型已成为制造业不可避免的趋势。为了应对市场快速变化、提高运营效率以及降低成本,制造业企业积极追求更加智能化、敏捷的生产方式。在这个转型过程中,低代码技术作为一种强大的工具,正逐渐崭露头角,有望加速制造业的数字化转型。

低代码技术简介
低代码技术是一种创新的应用开发方法,旨在简化和加速应用程序的开发过程。它通过提供可视化开发工具、模块化组件和自动化功能,使开发人员能够以最小的手动编码工作量快速创建高质量的应用程序。低代码平台的目标是降低应用开发的技术门槛,使非编程专业人员也能积极参与应用程序的创建,从而加快数字化转型的进程。
1.可视化开发:低代码平台通过提供可视化界面,使用户能够通过简单的拖放操作和图形化界面设计来创建应用程序。这种方式大大减少了手动编码的工作量,使开发过程更加简便。
2.模块化组件:低代码平台通常预构建了大量的组件,比如表单、数据库集成、报告生成等。开发人员可以直接使用这些组件,无需从头开始编写代码,从而大大提高了开发效率。
3.自动化:低代码平台通常具备自动化功能,如工作流程管理、规则引擎和自动测试等,这些功能简化了应用程序逻辑的开发和管理,使开发人员能够专注于业务逻辑和功能实现。

4.快速迭代:低代码技术使应用程序的快速开发和迭代成为可能。由于开发过程得到了极大的简化,企业可以更灵活地响应市场需求,及时更新和优化应用程序。
5.适应性和可扩展性:低代码应用程序通常具备良好的适应性和可扩展性。它们能够适应不同的设备、平台和屏幕尺寸,并具备应对不断增长的用户和数据需求的能力。这使得制造业企业能够根据市场需求和技术趋势,快速调整和扩展其业务应用程序。
通过利用低代码技术的优势,制造业企业可以加快数字化转型的进程,提高开发效率和质量,降低开发门槛和成本。在这个过程中,制造业企业需要敢于尝试、勇于创新,才能在快速变化的商业环境中保持竞争优势并实现持续发展。
制造业数字化转型中的低代码关键优势
在制造业领域,低代码技术的关键优势在于其快速应用开发能力。利用可视化开发工具和预构建的组件,制造企业可以更快地开发、测试和部署应用程序,以适应不断变化的市场需求。这种快速应用开发能力降低了开发成本,提高了开发效率,使企业能够更快地推出新产品或更新现有产品。
随着数字化转型的加速,低代码技术已成为制造业企业实现业务创新和提升竞争力的关键因素。低代码平台通过提供可视化界面和预构建组件,简化了应用程序的开发过程,使制造企业能够更快速地开发和部署应用程序,从而应对不断变化的市场需求。
快速应用开发:低代码平台使制造企业能够更快速地开发和部署应用程序,无需进行大量的手动编码。通过可视化开发工具和预构建的组件,开发人员可以快速构建和测试应用程序,加速数字化转型进程。这意味着企业可以更快地推出新产品或更新现有产品,抓住市场机会并满足客户需求。
降低技术门槛:低代码技术降低了应用开发的技术门槛,使非技术人员也能积极参与应用程序开发过程。这意味着制造企业可以利用内部资源,如业务分析师和产品经理等,而不仅仅依赖于专业开发人员。通过降低技术门槛,企业可以更高效地进行应用程序开发,并加快数字化转型的进程。
适应性和可扩展性:低代码应用程序具有适应性和可扩展性,可以根据不同的需求进行定制和扩展。这使制造业能够满足不同规模和类型的需求,从小型工厂到大型生产线。通过低代码平台的灵活性和可扩展性,企业可以轻松应对市场和技术的变化,保持竞争优势。
降低开发成本:由于低代码技术减少了手动编码工作,因此可以降低应用程序开发的成本。这使得数字化转型更具成本效益,特别是对于中小型企业而言。通过减少开发成本,企业可以将更多的资源和预算投入到核心业务和产品创新上,推动企业的发展。
快速迭代和改进:低代码平台有助于制造企业快速迭代应用程序,以适应市场需求的变化。这允许企业更敏捷地改进和优化其数字解决方案。通过快速迭代和改进,企业可以及时响应市场反馈和客户需求,提升客户满意度和市场竞争力。
跨平台兼容性:低代码应用程序可以跨不同的设备和操作系统运行,包括移动设备和桌面计算机。这增加了应用程序的可访问性,使员工能够在不同的设备上使用应用程序。通过跨平台兼容性,企业可以提供更便捷和高效的用户体验,满足员工和客户的需求。
自动化工作流程:利用低代码平台,制造企业可以创建自动化工作流程,以简化和优化生产和业务流程。这有助于提高效率、降低人为错误的可能性并减少成本。自动化工作流程可以涉及各种任务和流程的自动化,例如数据输入、审批流程和报告生成等。通过自动化工作流程,企业可以加快业务流程的执行速度并提高准确性。
整合能力:低代码技术具有良好的集成能力,可以与其他系统和数据源无缝连接。这使制造企业能够实现更全面的数据分析和决策支持。通过与其他系统集成,企业可以轻松地访问关键业务数据并实现数据驱动的决策。这有助于提高决策效率和准确性,推动企业的持续发展。
总结
低代码技术在制造业中崭露头角,成为加速数字化转型的重要武器。它以其强大的能力,帮助制造业提高竞争力、降低成本、提升效率以及激发创新能力。面对未来的众多挑战和机遇,制造业领导者需要积极探索和采用低代码技术,把握未来的先机。随着数字化转型的推进,制造业的未来将更加充满希望,而低代码技术在这一过程中将发挥至关重要的角色。

云表低代码平台在服务客户的过程中,不断丰富和拓展其数字化应用,已经形成了覆盖87个细分行业的上千种应用模板,且这些应用模板开箱即用,随需可调,让更多行业的组织能够快速实现数字化。
这些数字化应用不仅覆盖了各行各业,而且针对每个行业的特点和需求进行了精细化的设计和开发,能够满足不同行业的特定需求。无论是大型企业还是中小企业,无论是哪个行业,都可以在云表低代码平台上找到适合自己的数字化应用,快速实现数字化转型和发展。
相关文章:

数字化转型:云表低代码开发助力制造业腾飞
数字化转型已成为制造业不可避免的趋势。为了应对市场快速变化、提高运营效率以及降低成本,制造业企业积极追求更加智能化、敏捷的生产方式。在这个转型过程中,低代码技术作为一种强大的工具,正逐渐崭露头角,有望加速制造业的数字…...

Linux学习之vim跳转到特定行数
参考的博客:《Vim跳到最后一行的方法》 《oeasy教您玩转vim - 14 - # 行头行尾》 《Linux:vim 中跳到首行和最后一行》 想要跳到特定行的话,可以在命令模式和正常模式进行跳转。要是对于vim的四种模式不太熟的话,可以到博客《Linu…...

详解基于Android的Appium+Python自动化脚本编写
📢专注于分享软件测试干货内容,欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢交流讨论:欢迎加入我们一起学习!📢资源分享:耗时200小时精选的「软件测试」资…...
【马蹄集】—— 百度之星 2023
百度之星 2023 目录 BD202301 公园⭐BD202302 蛋糕划分⭐⭐⭐BD202303 第五维度⭐⭐ BD202301 公园⭐ 难度:钻石 时间限制:1秒 占用内存:64M 题目描述 今天是六一节,小度去公园玩,公园一共 N N N 个景点&am…...
大数据毕业设计选题推荐-无线网络大数据平台-Hadoop-Spark-Hive
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

【jvm】虚拟机之本地方法接口与本地方法库
目录 一、本地方法1.1 说明1.2 代码示例1.3 为什么要使用native method 二、现状 一、本地方法 1.1 说明 1.一个Native Method就是一个Java调用非Java代码的接口。 2.一个Native Method是这样一个Java方法:该方法的实现由非Java语言实现,比如C。 3.这个…...
HDFS系统操作命令大全
一,前言 HDFS作为分布式存储的文件系统,有其对数据的路径表达方式 HDFS同linux系统一样,均是以/作为根目录的组织形式 linux:/usr/local/hello.txt HDFS:/usr/local/hello.txt 二,如何区分呢? L…...

雷尼绍探头编程 9810
9810 安全移动 使用参数 参数含义#9移动速度 F#117移动速度 F#148#24X 移动 终点绝对坐标#25Y 移动 终点绝对坐标#26Z 移动 终点绝对坐标#123机床移动到终点的绝对坐标 与 终点的理论值 的 差#5041当前绝对坐标 X 值#5042当前绝对坐标 Y 值#5043当前绝对坐标 Z 值#116刀具…...
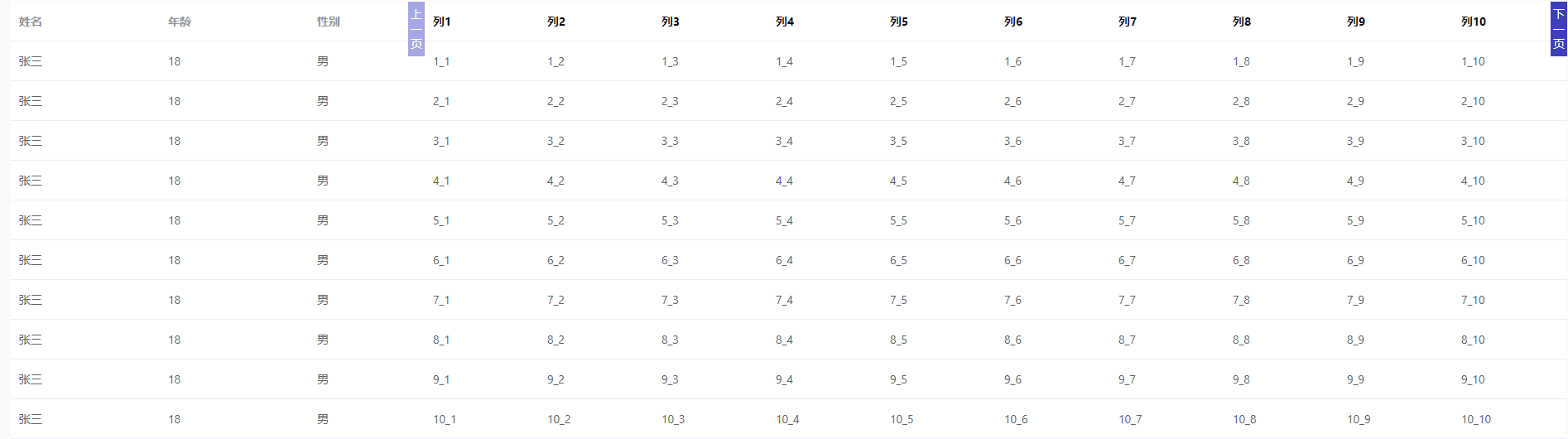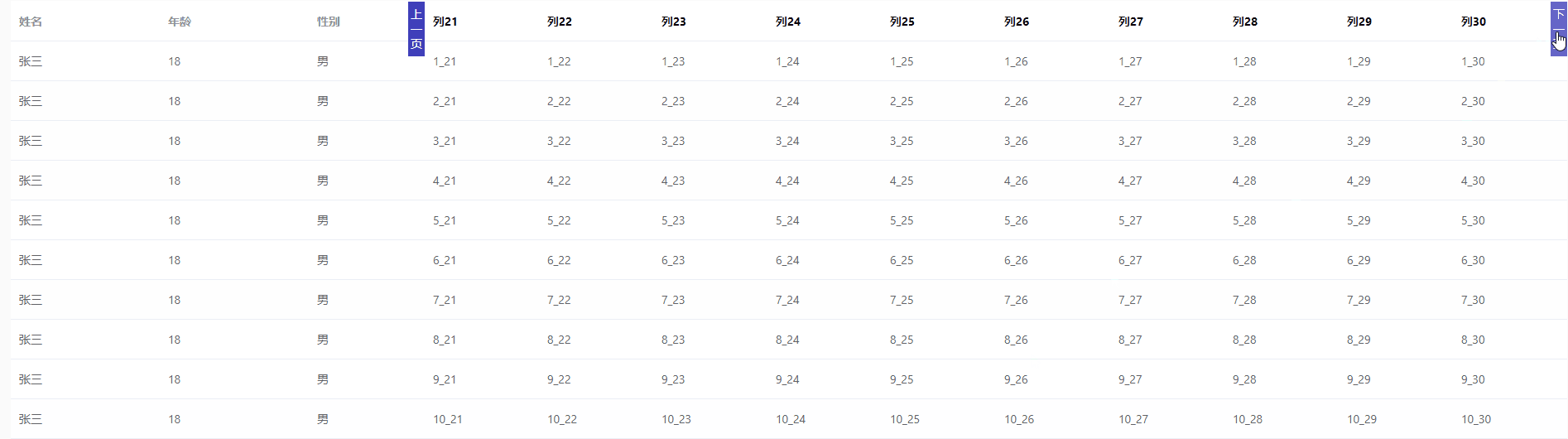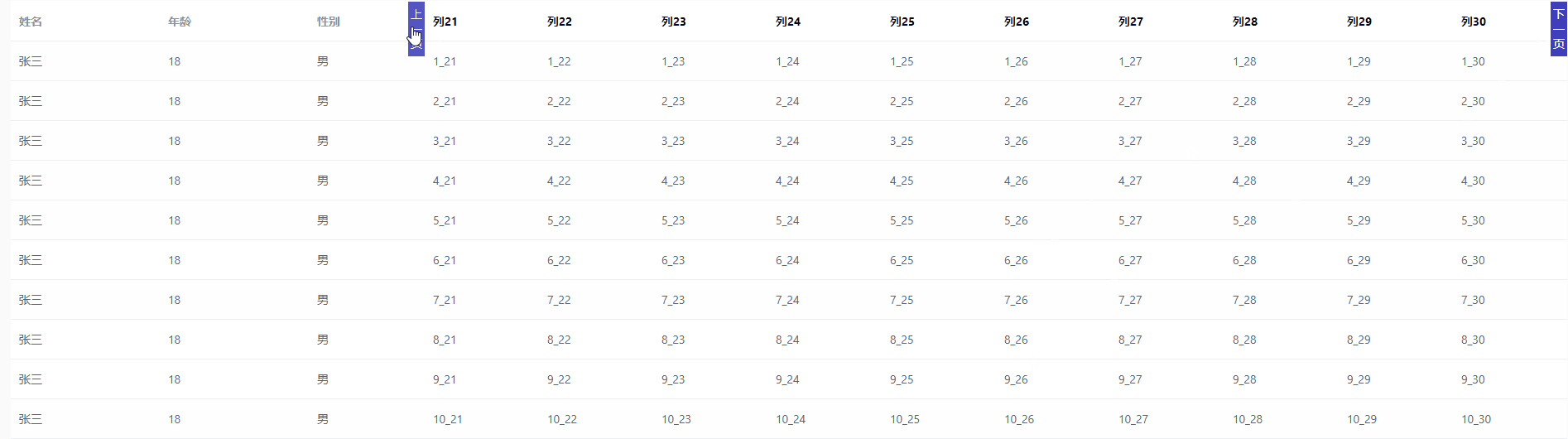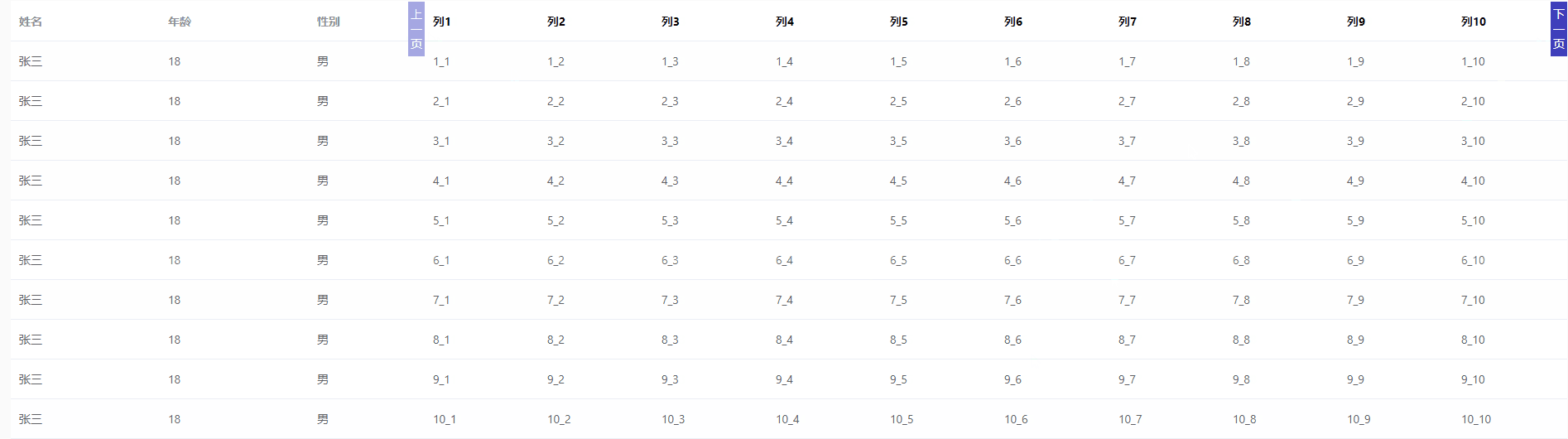
el-table 列分页
<template><div><el-table:data"tableData":key"tampTime"style"width: 100%"><el-table-columnprop"name"label"姓名"width"180"></el-table-column><el-table-columnprop&quo…...

APP攻防--ADB基础
进入app包 先使用 adb devices查看链接状态 手机连接成功的 adb shell 获取到手机的一个shell 此时想进入app包时没有权限的,APP包一般在data/data/下。没有执行权限,如图 Permission denied 权限被拒绝 此时需要手机root,root后输入 su …...
【Linux】第十站:git和gdb的基本使用
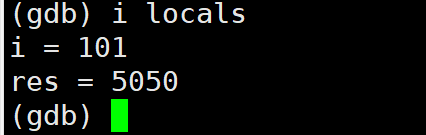
文章目录 一、git的基本操作1.gitee新建仓库注意事项2.git的安装3.git的克隆4.git的add5.git的commit6.git的push7.git log8.git status9. .gitignore 二、Linux调试器---gdb1.背景2.gdb安装、进入与退出3.list/l4.r/run运行程序5. break/b 打断点6.info/i b 查看断点7.delete/…...

Single Image Haze Removal Using Dark Channel Prior(暗通道先验)
去雾算法都会依赖于很强的先验以及假设,并结合相应的物理模型,完成去雾过程。本文作者何凯明及其团队通过大量的无雾图像和有雾图像,归纳总结出无雾图像在其对应的暗通道图像上具有极低的强度值(趋近于0),并…...
)
力扣382.链表随机节点(java利用数组随机返回节点值)
Problem: 382. 链表随机节点 文章目录 思路解题方法复杂度Code 思路 注意链表与数组的特性,对于随机访问读取的操作利用数组可以较方便实现,所以我们可以将链表中的节点值先存入到数组中最后再取出随机生成节点位置的值。 解题方法 1.生成List集合与Rand…...
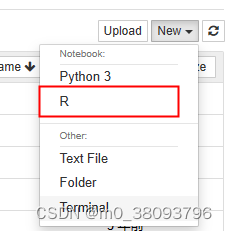
在jupyter中使用R
如果想在Jupyter Notebook中使用R语言,以下几个步骤操作可行: 1、启动Anaconda Prompt 2、进入R的安装位置,切换到R的安装位置:D:\Program Files\R\R-3.4.3\bin,启动R,具体代码操作步骤如下,在…...

2023(第四届)江西开放数据创新应用大赛等你来挑战!
邀请函 这是一个友好的邀请。无论你是数据领域的专家、学生还是爱好者,我们都欢迎你加入这个平台。这不仅仅是一场比赛,更是一个交流、学习和展示自己的机会。 丰厚奖金:我们为参赛者准备了总计15W的奖金池,期待你的才华在这里得…...

2023-mac rz sz 安装
之前安装过一次,没问题,这次按照之前教程装了就不管上传下载都会卡住; step1: brew install lrzsz step2:在/usr/local/bin 路径下配置两个sh,之前从网上找到的直接用都不对,下面这个是调试过的正式可用的 iterm2…...
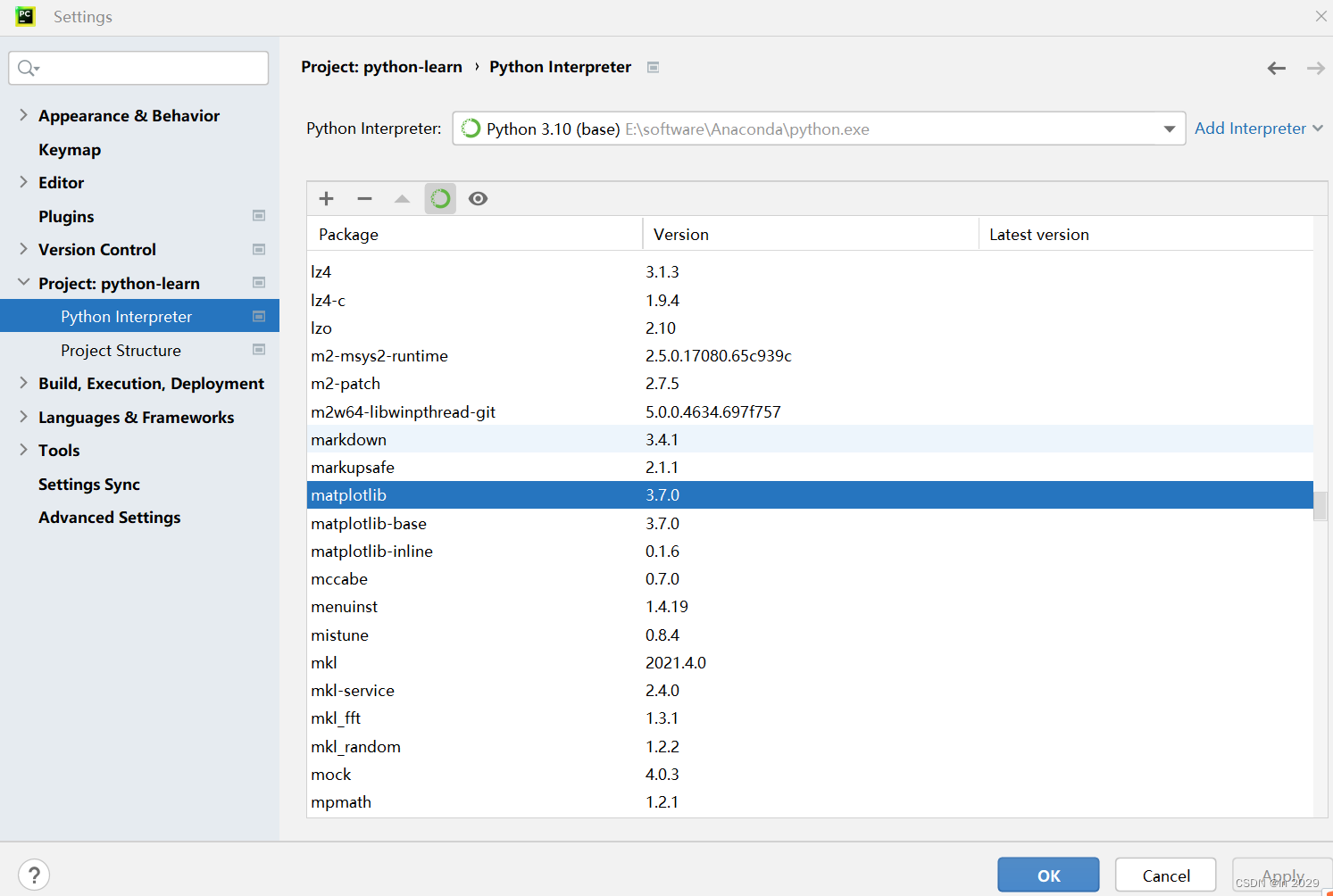
使用Matplotlib绘画3D图时运行不出结果,也不报错,图片是空白 !!
1.问题: 我使用如下代码运用matplotlib中的Axes3D绘画3D图,但是运行出来的结果是空白。 import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D #导入3D包 fig plt.figure() #窗口 #ax Axes3D(fig) # X, Y …...

Matlab函数——find
介绍 当你需要返回某个数组中符合指定条件的所有元素的索引时,可以使用 MATLAB 中的 find 函数。 find 函数语法: indices find(X) indices find(X, k) indices find(X, k, first) indices find(X, k, last) 其中,X 是一个数组…...
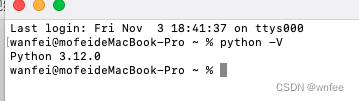
mac安装python3
文章目录 1. 安装1.1 brew安装(失败)2. 下载安装包 2. 查看版本3. 配置 1. 安装 1.1 brew安装(失败) brew install python3下载完成后报错:Error: python3.10: unknown or unsupported macOS version: :dunno 解决&a…...
【星海出品】VUE(一)
Windows安装nvm控制器 Windows里找都PowerShell。右击点击管理员运行。 1.安装choco Set-ExecutionPolicy Bypass -Scope Process -Force; iex ((New-Object System.Net.WebClient).DownloadString(https://chocolatey.org/install.ps1))2.安装NVM choco install nvm 3.查看可…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
